2010广州中考数学番禺一模试题与答案 9页

番禺区2010年九年级数学综合训练试题 本试卷分选择题和非选择题两部分，共三大题25小题，满分150分．考试时间为120分钟．‎ 注意事项：‎ ‎1.答卷前，考生务必在答题卡第1页上用黑色字迹的钢笔或签字笔填写自己的考生号、姓名；填写考场试室号、座位号，再用2B铅笔把对应这两个号码的标号涂黑．‎ ‎2.选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号；不能答在试卷上．‎ ‎3.非选择题必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用2B铅笔画图．答案必须写在答题卡各题目指定区域内的相应位置上；如需要改动，先划掉原来的答案，然后再写上新的答案；改动的答案也不能超出指定的区域．不准使用铅笔、圆珠笔和涂改液．不按以上要求作答的答案无效．‎ ‎4.考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回．‎ 第一部分 选择题（共30分）‎ 一、选择题（本大题共10小题，每小题3分，满分30分．在每小题给出的四个选项中 只有一项是符合题目要求的.）‎ ‎1．下列运算正确的是（※）．‎ ‎（A）2+=3+ （B）2= （C）2·=3 （D）÷=‎ ‎1‎ ‎2‎ a b 图1‎ ‎2．如图1，已知，，那么的大小为（※）．‎ ‎ (A) (B) (C) (D) ‎ ‎3．若=，=，则的值为（※）．‎ ‎（A） （B） （C） （D）‎ ‎4．已知三角形的两边长分别为‎3cm和‎8cm，则此三角形的第三边 的长不可能是（※）．‎ ‎（A）‎7cm （B）‎6cm （C）‎3cm （D）‎‎8cm ‎5. 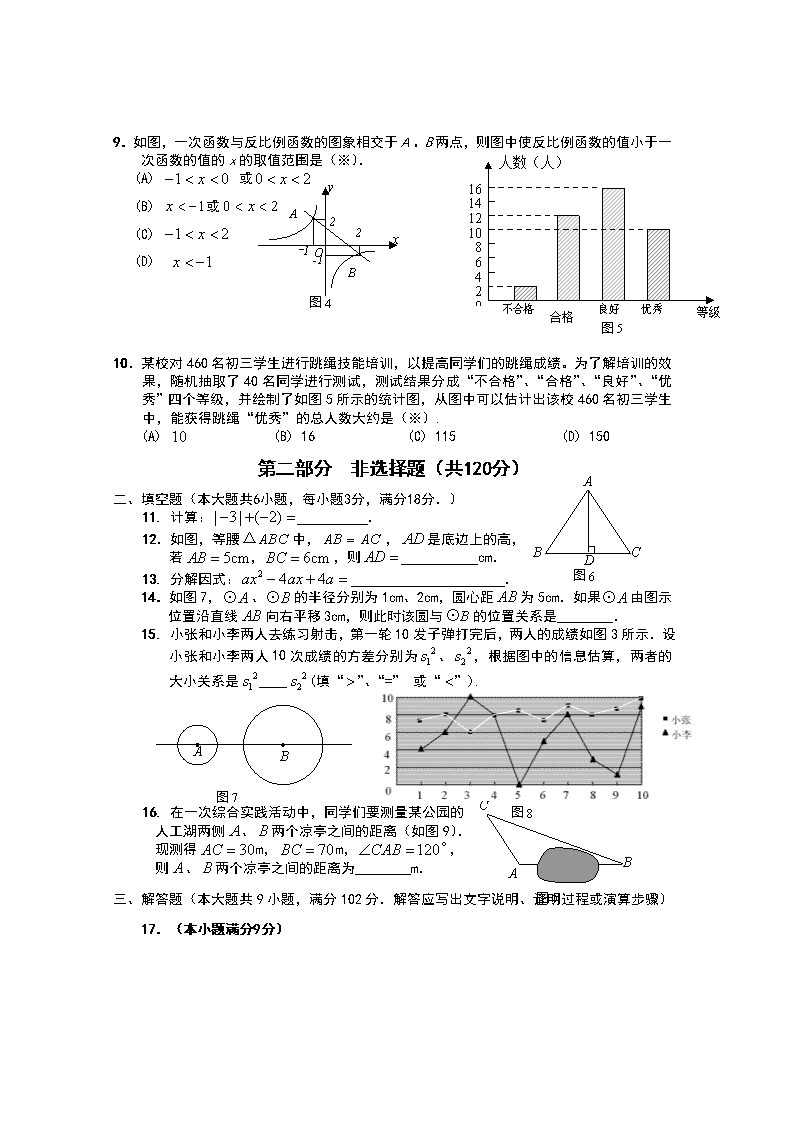甲型Ｈ1N1流感病毒的直径大约是0.000 000 ‎081米，用科学记数法可表示为（※）．‎ ‎（A）8.1×‎1‎米　　（B）8.1×‎1‎米　 （C）81×‎1‎米　　（D）0.81×‎‎1‎米 ‎6．在平面直角坐标系中，已知点A（0，2），B（，0），C（0，），D（，0），则以这四个点为顶点的四边形是（※）．‎ 图2‎ ‎ (A) (B) (C) (D)‎ ‎ 图3‎ ‎（A）矩形 （B）菱形 （C）正方形 （D）梯形 ‎7．已知关于的方程的一个根为，‎ 则实数的值为（※）．‎ ‎（A）1 （B） （C）2 （D）‎ ‎8．如图2是一根钢管的直观图，则它的三视图为（※）．‎ 图5‎ 人数（人）‎ 不合格 良好 优秀 等级 ‎16‎ ‎14‎ ‎12‎ ‎10‎ ‎8‎ ‎6‎ ‎4‎ ‎2‎ ‎0‎ 合格 ‎9．如图，一次函数与反比例函数的图象相交于Ａ、B两点，则图中使反比例函数的值小于一次函数的值的x的取值范围是（※）．‎ 图4‎ ‎-1‎ ‎2‎ ‎2‎ x y A B O O ‎-1‎ O ‎(A) 或 ‎ ‎ (B) 或 ‎ (C) ‎ ‎(D) ‎ ‎10．某校对460名初三学生进行跳绳技能培训，以提高同学们的跳绳成绩。为了解培训的效果，随机抽取了40名同学进行测试，测试结果分成“不合格”、“合格”、“良好”、“优秀”四个等级，并绘制了如图5所示的统计图，从图中可以估计出该校460名初三学生中，能获得跳绳“优秀”的总人数大约是（※）.‎ ‎(A) (B) 16 (C) 115 (D) 150‎ A C D B 图6‎ 第二部分 非选择题（共120分）‎ 二、填空题（本大题共6小题，每小题3分，满分18分．）‎ ‎11. 计算： ．‎ ‎12．如图，等腰中，，是底边上的高，‎ 若，则 cm．‎ ‎13. 分解因式： ．‎ ‎14．如图7，、的半径分别为‎1cm、‎2cm，圆心距为‎5cm．如果由图示位置沿直线向右平移‎3cm，则此时该圆与的位置关系是________． ‎ 图8‎ ‎15. 小张和小李两人去练习射击，第一轮10发子弹打完后，两人的成绩如图3所示．设小张和小李两人10次成绩的方差分别为、，根据图中的信息估算，两者的大小关系是____(填“”、“=” 或“”).‎ B A 图7‎ C B A 图9‎ ‎16. 在一次综合实践活动中，同学们要测量某公园的 人工湖两侧、两个凉亭之间的距离（如图9）．‎ 现测得m，m，，‎ 则、两个凉亭之间的距离为________m．‎ 三、解答题（本大题共9小题，满分102分．解答应写出文字说明、证明过程或演算步骤）‎ ‎17．（本小题满分9分）‎ 如图10，点A、B在数轴上，它们所对应的数分别是、，且点A、B关于原点对称.‎ A B ‎0‎ 图10‎ ‎（1）写出点B所对应的实数，并求线段的长；‎ ‎（2）求的值．‎ ‎18．（本小题满分９分）‎ ‎1‎ ‎2‎ ‎3‎ ‎0‎ 图11‎ 解不等式组 ,并把它的解集在数轴上表示出来．‎ ‎19.（本小题满分10分）‎ 图12‎ D C E A F B 如图11，已知在中，，为边的中点，‎ 过点作，垂足分别为.‎ ‎（1）求证：；‎ ‎（2）当时，试判断四边形是何特殊 四边形？并说明理由.‎ ‎20．（本小题满分10分）‎ 有3个完全相同的乒乓球，把它们分别标号为1，2，3后放入一个不透明的口袋中，随机地摸出一个球后不放回，再随机地摸出另一个球．‎ ‎（1）试用树形图法（或列表法）列出两次摸球出现的所有可能结果；‎ ‎（2）求摸出的两个球号码之和为奇数的概率．‎ ‎21．(本题满分12分) ‎ 为迎接即将在我市召开的第16届亚运会，某工厂准备承接生产本届亚运会会标和亚运会吉祥物“乐羊羊”的生产任务，需要用到甲、乙两种原料。已知生产一套亚运会标志需要甲原料和乙原料分别为‎0.4kg和‎0.3kg，生产一套亚运会吉祥物需要甲原料和乙原料分别为‎0.5kg和‎1kg．该厂购进甲、乙原料的量分别为‎2000kg和‎3000kg，如果所进原料全部用完，求该厂能生产亚运会标志和亚运会吉祥物各多少套？ ‎ ‎22．（本小题满分１2分）‎ ‎ 图12‎ 已知：如图12，在中，，点在上，以为圆心，长为半径的圆与分别交于点，且．‎ ‎（1）判断直线与⊙的位置关系，并证明你的结论；‎ ‎（2）若，求⊙的面积．‎ ‎23．（本小题满分１2分） ‎ 已知：关于的一元二次方程．‎ ‎（1）若, 求出此时方程的实数根；‎ ‎（2）求证：方程总有实数根；‎ ‎（3）设,方程的两个实数根分别为，（其中）．若是关于的函数，且，求函数的解析式, 并画出其图象（画草图即可, 不必列表）.‎ ‎24．（本小题满分14分） ‎ 在中，，，点是上一动点（不与重合），将线段绕点逆时针旋转后到达位置，连接、，设．‎ ‎（1）如图14，若，求的大小；‎ ‎（2）如图15，当点在线段上运动时，试探究之间的数量关系？并对你的结论给出证明；‎ ‎（3）当点在线段的反向延长线上运动时，（2）中的结论是否仍然成立？若成立，试加以证明，若不成立，试找出之间的新关系，并说明理由。‎ 图16‎ 图15‎ 图14‎ ‎25．（本小题满分14分）‎ 如图，已知抛物线与轴交于 ‎、,与轴交于点.‎ ‎（1）求此抛物线的函数表达式, 写出它的对称轴；‎ ‎（2）若在抛物线的对称轴上存在一点，使的周长最小, 求点的坐标;‎ ‎（3）若点为线段上的一个不与端点重合的动点, 过点作交于点,连结、,设的面积为,求当点运动到何处时的值最大?‎ ‎2010学年第二学期九年级数学综合练习 参考答案与评分说明 ‎ 一、选择题（本大题共10小题，每小题3分） ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B C D C C B A D B C 二、填空题答案栏（每小题3分，共18分）‎ ‎11. 1； 12.4; 13.；14.相交；15.；16.50. ‎ 三、解答题（本大题共9小题，满分102分．解答应写出文字说明、证明过程或演算步骤）‎ 三、17．解：（1）B所对应的实数为4, 2分 ‎ 4分 ‎（2）由题意得，， 6分 解得． 8分 经检验，是原方程的解．‎ 的值为． 9分 三、18.解：‎ 由①得， 3分 由②得， 5分 原不等式组的解集为 7分 不等式的解集在数轴上表示如图. 9分 三、19证明（1）， ‎ ‎， 1分 ‎，图12‎ D C E A F B ， 3分 是的中点，‎ ‎， 4分 ‎. 5分 ‎（2）四边形为正方形． 7分 ‎，‎ ‎，‎ ‎，四边形为矩形. 9分 又，‎ ‎，四边形为正方形． 10分 三、20．‎1‎ ‎2‎ ‎3‎ ‎2‎ ‎1‎ ‎3‎ ‎3‎ ‎1‎ ‎2‎ 第一个球 第二个球 解（1）法一：根据题意，可以画出如下的树形图：‎ ‎ 5分 从树形图可以看出，摸出两球出现的所有可能结果共有6种；‎ 法二：根据题意，可以列出下表：‎ 第二个球 第一个球 ‎（1，3）‎ ‎（2，3）‎ ‎（1，2）‎ ‎（3，2）‎ ‎（3，1）‎ ‎（2，1）‎ ‎3‎ ‎2‎ ‎1‎ ‎1‎ ‎2‎ ‎3‎ 从上表中可以看出，摸出两球出现的所有可能结果共有6种. 5分 ‎（2）设两个球号码之和是奇数为事件.‎ 摸出的两个球号码之和是奇数的结果有4种，它们是：、、、‎ ‎ 10分 三、21．解：设生产亚运会标志x套，生产亚运会吉祥物y套． 2分 根据题意，得 6分 ‎①×2－②×1得：0.5x=1000．　‎ ‎∴ x=2000． 9分 把x=2000代入②得：600+y=3600．‎ ‎∴ y=3000． 11分 ‎ 答：该厂能生产亚运会标志2000套，生产亚运会吉祥物3000套． 12分 三、22．解：（1）直线与⊙相切．… 1分 证明：如图1，连结． …………… 2分 ‎，．…………… 3分 ‎， ．‎ 又， ………………………… 5分 ‎．‎ ‎．直线与⊙相切． 6分 ‎（2）连、 ． 7分 在中，，‎ ‎,即有 8分 由，得． 10分 又,为等边三角形,. 10分 即⊙的半径，故⊙的面积 12分 三、23．解:（1）若, 方程化为 2分 即,得或,‎ ‎. 4分 ‎（2）证明：是关于的一元二次方程，‎ ‎． 6分 ‎，，即．‎ 方程有实数根． 8分 ‎（3）解：由求根公式，得．‎ y 或． 9分 ‎3‎ ‎4‎ ‎，．‎ ‎2‎ ‎，‎ ‎-1‎ ‎-3‎ ‎-2‎ ‎-1‎ O x ‎1‎ ‎4‎ ‎3‎ ‎2‎ ‎1‎ ‎，． ‎ ‎-2‎ ‎-3‎ ‎．‎ 即为所求． 10分 此函数为反比例函数, 其图象如图所示． 12分 三、24．解：（1）,,. 1分 ‎ 2分 又 ‎≌, 3分 ‎.‎ ‎ ． 4分 ‎（2）． 6分 证明：∵，‎ ‎∴．即．‎ 又，∴． 8分 ‎∴．‎ ‎∴．∴． 9分 ‎∵，∴． 10分 ‎（3）当点在线段的反向延长线上运动时，（2）中的结论不能成立, 此时: 成立．‎ ‎ 12分 其理由如下: 类似（2）可证≌,从而.‎ 又由三角形外角性质有, 13分 而, ‎ ‎. 14分 三、25．解: （1）抛物线与轴交于点,‎ ‎. 1分 而抛物线过点、, 3分 解得.即此抛物线的函数表达式为. 4分 它的对称轴为直线. 5分 ‎（2）、关于对称轴直线对称, 在对称轴上,‎ ‎ 6分 所以当点共线时, 的周长最小. 7分 直线的解析式是:, 8分 令得.即点的坐标为(-2,-4) 9分 ‎（3）点为线段上的一个不与端点重合的动点, 10分 ‎,‎ ‎,,‎ 而,,即 10分 的面积 11分 即 13分 当时,的值最大, 最大值为. 14分