中考数学规律复习题整理全含答案 16页

规律探索 1 一．选择题 1．观察下列等式：31＝3，32＝9，33＝27，34＝81，35＝243，36＝729，37＝2187… 解答下列问题：3＋32＋33＋34…＋32013 的末位数字是（　　） A．0 B．1 C．3 D．7 2. 把所有正奇数从小到大排列，并按如下规律分组： （1），（3，5，7），（9，11，13，15，17），（19，21，23，25，27，29，31），…， 现用等式 AM=（i，j）表示正奇数 M 是第 i 组第 j 个数（从左往右数），如 A7=（2，3），则 A2013=（ ） A．（45，77） B．（45，39） C．（32，46） D．（32，23） 3.下表中的数字是按一定规律填写的，表中 a 的值应是 ． 1 2 3 5 8 13 a … 2 3 5 8 13 21 34 … 4.下列图形都是由同样大小的矩形按一定的规律组成，其中 第（1）个图形的面积为 2cm2，第（2）个图形的面积为 8 cm2， 第（3）个图形的面积为 18 cm2，……，第（10）个图形的面积为（ ） A．196 cm2 B．200 cm2 C．216 cm2 D． 256 cm2 5．如图，动点 P 从（0，3）出发，沿所示的方向运动，每当碰到矩形的边时反弹， 反弹时反射角等于入射角，当点 P 第 2013 次碰到矩形的边时，点 P 的坐标为（ ） A、（1，4） B、（5，0） C、（6，4） D、（8，3） 6．如图，下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中 M 与 m、n 的关系是 A． M=mn B． M=n(m+1) C．M=mn+1 D．M=m(n+1) 7．我们知道，一元二次方程 没有实数根，即不存在一个实数的平方等于-1，12 −=x 若我们规定一个新数“”，使其满足 (即方程 有一个根为)， 并且进一步规定: 一切实数可以与新数进行四则运算，且原有的运算律和运算法则仍然成立， 于是有 ， 从而对任意正整数 n， 我们可得到 同理可得 那么， 的值为( ) A．0　　B．1　　　C．-1　　　D． i 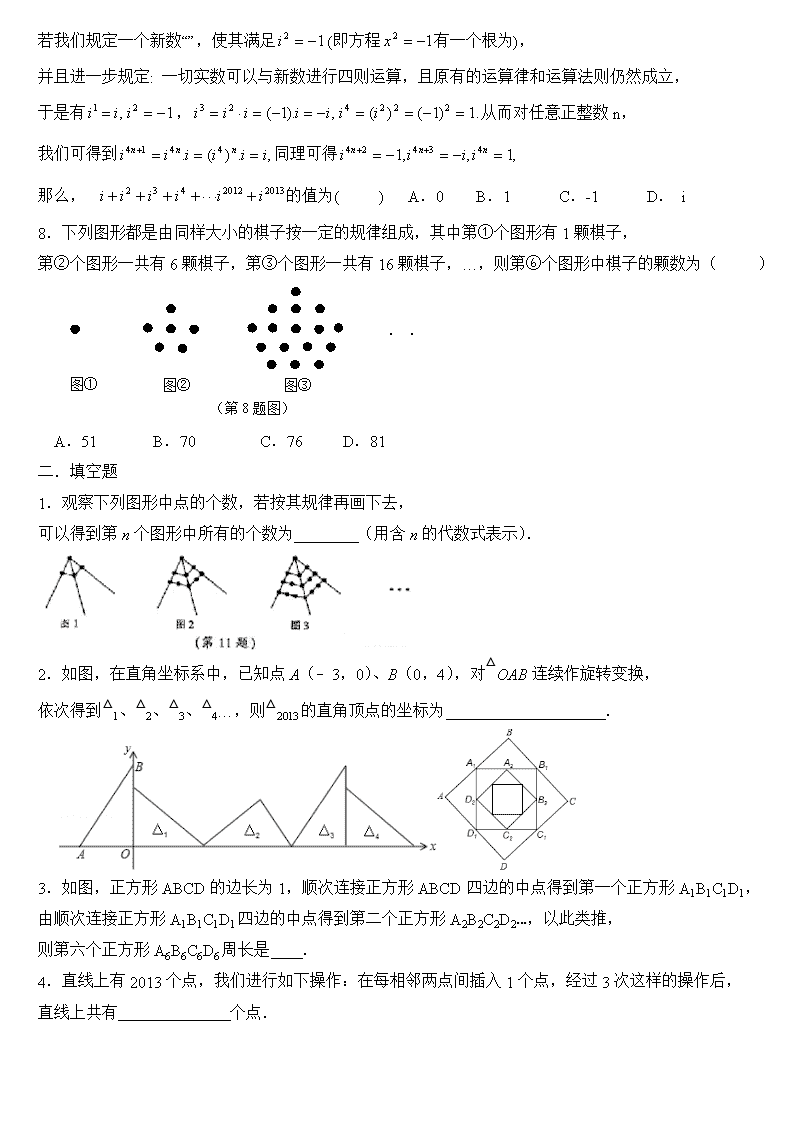8．下列图形都是由同样大小的棋子按一定的规律组成，其中第①个图形有 1 颗棋子， 第②个图形一共有 6 颗棋子，第③个图形一共有 16 颗棋子，…，则第⑥个图形中棋子的颗数为（ ） A．51 B．70 C．76 D．81 二．填空题 1．观察下列图形中点的个数，若按其规律再画下去， 可以得到第 n 个图形中所有的个数为 （用含 n 的代数式表示）． 2．如图，在直角坐标系中，已知点 A（﹣3，0）、B（0，4），对△OAB 连续作旋转变换， 依次得到△1、△2、△3、△4…，则△2013 的直角顶点的坐标为 ． 3．如图，正方形 ABCD 的边长为 1，顺次连接正方形 ABCD 四边的中点得到第一个正方形 A1B1C1D1， 由顺次连接正方形 A1B1C1D1 四边的中点得到第二个正方形 A2B2C2D2…，以此类推， 则第六个正方形 A6B6C6D6 周长是　　． 4．直线上有 2013 个点，我们进行如下操作：在每相邻两点间插入 1 个点，经过 3 次这样的操作后， 直线上共有 个点． 12 −=i 12 −=x ,1 ii = 12 −=i ,).1(23 iiiii −=−=⋅= .1)1()( 2224 =−== ii ,.)(. 4414 iiiiii nnn ===+ ,1,,1 43424 =−=−= ++ nnn iiii 20132012432 iiiiii +⋅⋅⋅++++ 图① 图② 图③ · · · （第 8 题图） 5．如图，古希腊人常用小石子在沙滩上摆成各种形状来研究数． 例如：称图中的数 1，5，12，22…为五边形数，则第 6 个五边形数是　 　． 6 ．如图，是用火柴棒拼成的图形，则第 n 个图形需　 　根火柴棒． 7．观察规律：1=12；1+3=22；1+3+5=32；1+3+5+7=42；…，则 1+3+5+…+2013 的值是　 　． 8．如图 12，一段抛物线：y＝－x(x－3)（0≤x≤3），记为 C1，它与 x 轴交于点 O，A1； 将 C1 绕点 A1 旋转 180°得 C2，交 x 轴于点 A2； 将 C2 绕点 A2 旋转 180°得 C3，交 x 轴于点 A3； …… 如此进行下去，直至得 C13．若 P（37，m） 在第 13 段抛物线 C13 上，则 m =_________． 9.直线上有 2013 个点，我们进行如下操作：在每相邻两点间插入 1 个点，经过 3 次这样的操作后， 直线上共有 个点. 10．观察下列各式的计算过程：5×5=0×1×100+25，15×15=1×2×100+25， 25×25=2×3×100+25，35×35=3×4×100+25，…… …… 请猜测，第 n 个算式(n 为正整数)应表示为____________________________． 11．将连续的正整数按以下规律排列，则位于第 7 行、第 7 列的数 是__ __．x 12、如下图，每一幅图中均含有若干个正方形，第①幅图中含有 1 个正方形； 第②幅图中含有 5 个正方形；……按这样的规律下去，则第（6）幅图中含有 个正方形； 13．将一些半径相同的小圆按如图所示的规律摆放： 第 1 个图形有 6 个小圆， 第 2 个图形有 10 个小圆， 第 3 个图形有 16 个小圆， 第 4 个图形有 24 个小 圆， ……，依次规律，第 6 个图形有　　　　个小圆． 14.已知一组数 2，4，8，16，32，…，按此规律，则第 n 个数是　 　． 15、我们知道，经过原点的抛物线的解析式可以是 y＝ax2＋bx(a≠0) （1）对于这样的抛物线： 当顶点坐标为（1，1）时， ＝__________； 当顶点坐标为（m，m），m≠0 时， 与 m 之间的关系式是__________； （2）继续探究，如果 b≠0，且过原点的抛物线顶点在直线 y＝kx(k≠0)上，请用含 的代数式表示 b； （3）现有一组过原点的抛物线，顶点 A1，A2，…，An 在直线 y＝x 上， 横坐标依次为 1，2，…，n（为正整数，且 n≤12）， 分别过每个顶点作 轴的垂线，垂足记为 B1，B2，…，Bn，以线段 AnBn 为边向右作正方形 AnBnCnDn， 若这组抛物线中有一条经过 Dn，求所有满足条件的正方形边长． a a k x •••••• ① ② ③ 16．如图，所有正三角形的一边平行于 x 轴，一顶点在 y 轴上，从内到外， 它们的边长依次为 2，4，6，8，…，顶点依次用 、 、 、 、…表示， 其中 与 x 轴、底边 与 、 与 、…均相距一个单位， 则顶点 的坐标是 ， 的坐标是 ． 第 16 题图 17．如图，已知直线 l：y= x，过点 A（0，1）作 y 轴的垂线交直线 l 于点 B， 过点 B 作直线 l 的垂线交 y 轴于点 A1；过点 A1 作 y 轴的垂线交直线 l 于点 B1， 过点 B1 作直线 l 的垂线交 y 轴于点 A2；……按此作法继续下去，则点 A2013 的坐标为 ． 18、如图，在平面直角坐标系中，一动点从原点 O 出发，按向上，向右，向下，向右的方向不断地移动， 每移动一个单位，得到点 A1（0，1），A2（1，1），A3（1，0），A4（2，0），… 那么点 A4n＋1（n 为自然数）的坐标为 （用 n 表示） 1A 2A 3A 4A 1 2A A 1 2A A 4 5A A 4 5A A 7 8A A 3A 22A x y A9 A6 A3 A8A7 A5A4 A2A1 O 3 3 19．当白色小正方形个数 等于 1，2，3…时，由白色小正方形和和黑色小正方形组成的图形分别如图所 示． 则第 个图形中白色小正方形和黑色小正方形的个数总和等于__________．（用 表示， 是正整数） 20. （2013•衢州 4 分）如图，在菱形 ABCD 中，边长为 10，∠A=60°．顺次连结菱形 ABCD 各边中点，可 得四边形 A1B1C1D1；顺次连结四边形 A1B1C1D1 各边中点，可得四边形 A2B2C2D2；顺次连结四边 形 A2B2C2D2 各边中点，可得四边形 A3B3C3D3；按此规律继续下去…．则四边形 A2B2C2D2 的周长是　 　； 四边形 A2013B2013C2013D2013 的周长是　　 ． 21.一组按规律排列的式子：ａ２， ， , ,….则第 n 个式子是________ 22.观察下面的单项式：a，﹣2a2，4a3，﹣8a4，…根据你发现的规律，第 8 个式子是　 　． 23.如图，已知直线 l：y= x，过点 M（2，0）作 x 轴的垂线交直线 l 于点 N，过点 N 作直线 l 的垂线交 x 轴于点 M1；过点 M1 作 x 轴的垂线交直线 l 于 N1，过点 N1 作直线 l 的垂线交 x 轴于点 M2，…；按此作法 继续下去，则点 M10 的坐标为　 ． 24.为庆祝“六•一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛．如图所示：按照上面的规律， 摆第（n）图，需用火柴棒的根数为　 　． n n n n 4 3 a 6 5 a 8 7 a 答案： 选择题：1、C 2、C 3、21 4、B 5、D 6、D 7、D 8、 C 填空题：1、（n+1）2 2、（8052,0） 3、0.5 4、16097 5、51 6、2n+1 7、1014049 8、2 9、16097 10、[10(n-1)+5]2=100n(n-1)+25 11、85 12、91 13、46 14、2n 15、（1）－1；a＝－ （或 am＋1＝0） （2）解：∵a≠0 ∴y＝ax2＋bx ＝a(x＋ )2－ ∴顶点坐标为（－ ，－ ） ∵顶点在直线 y＝kx 上 ∴k(－ )＝－ ∵b≠0 ∴b＝2k （3）解：∵顶点 An 在直线 y＝x 上 ∴可设 An 的坐标为（n，n），点 Dn 所在的抛物线顶点坐标 为（t，t） 由（1）（2）可得，点 D n 所在 的抛物线解析式为 y＝－ x2＋2x ∵四边形 AnBnCnDn 是正方形 ∴点 Dn 的坐标为（2n，n） ∴－ (2n)2＋2×2n＝n ∴4n＝3t ∵t、n 是正整数，且 t≤12，n≤12 ∴n＝3，6 或 9 ∴满足条件的正方形边长为 3，6 或 9 16、（0， ），（－8，－8）. 17、 （注：以上两答案任选一个都对） 18、（2n，1） 19、n2+4n 20、20； 21、 （n 为正整数） 22、-128a8 23、（884736,0） 24、6n+2 1 m 2 b a 2 4 b a 2 b a 2 4 b a 2 b a 2 4 b a 1 t 1 t 3 1− ( ) ( )2013 40260,4 0,2或 2 2 1 na n - 规律探索 2 1、 我们平常用的数是十进制数，如 2639=2×103+6×102+3×101+9×100，表示十进制的数要用 10 个数码 （又叫数字）：0，1，2，3，4，5，6，7，8，9。在电子数字计算机中用的是二进制，只要两个数码：0 和 1。如二进制中 101=1×22+0×21+1×20 等于十进制的数 5，10111=1×24+0×23＋1×22＋1×21＋1×20 等 于十进制中的数 23，那么二进制中的 1101 等于十进制的数 。 2、 从 1 开始，将连续的奇数相加，和的情况有如下规律：1=1=12；1+3=4=22；1+3+5=9=32； 1+3+5+7=16=42；1+3+5+7+9=25=52；…按此规律请你猜想从 1 开始，将前 10 个奇数（即当最后一个奇数是 19 时），它们的和是 。 3、小王利用计算机设计了一个计算程序，输入和输出的数据如下表： 输入 … 1 2 3 4 5 … 输出 … … 那么，当输入数据是 8 时，输出的数据是（ ） A、 B、 C、 D、 4、如下左图所示，摆第一个“小屋子”要 5 枚棋子，摆第二个要 11 枚棋子，摆第三个要 17 枚棋子，则摆 第 30 个“小屋子”要 枚棋子. 5、如下右图是某同学在沙滩上用石子摆成的小房子，观察图形的变化规律，写出第 n 个小房子用了 块石子 6、如下图是用棋子摆成的“上”字： 第一个“上”字 第二个“上”字 第三个“上”字 如果按照以上规律继续摆下去，那么通过观察，可以发现：（1）第四、第五个“上”字分别需用 和 枚棋子；（2）第 n 个“上”字需用 枚棋子。 7、如图一串有黑有白，其排列有一定规律的珠子，被盒子遮住一部分，则这串珠子被盒子遮住的部分有_______ 颗. 2 1 5 2 10 3 17 4 26 5 61 8 63 8 65 8 67 8 (1) (2) (3) 第 4 题 第 7 题图 (1) (2) (3) (4) 8、根据下列 5 个图形及相应点的个数的变化规律：猜想第 6 个图形有 个点，第 n 个图形中有 个点。 9、下面是按照一定规律画出的一列“树型”图： 经观察可以发现：图（2）比图（1）多出 2 个“树枝”；图（3）比图（2）多出 5 个“树枝”；图（4）比 图（3）多出 10 个“树枝”；照此规律，图（7）比图（6）多出 个“树枝”。 10、观察下面的点阵图和相应的等式，探究其中的规律： （1）在④和⑤后面的横线上分别写出相应的等式； （2）通过猜想写出与第n 个点阵相对应的等式_____________________。 11、用边长为 1cm 的小正方形搭成如下的塔状图形，则第 n 次所搭图形的周长是_______________cm（用含 n 的代数式表示）。 12、如图，都是由边长为 1 的正方体叠成的图形。例如第（1）个图形的表面积为 6 个平方单位，第（2） 个图形的表面积为 18 个平方单位，第（3）个图形的表面积是 36 个平方单位。依此规律。则第（5）个图 形的表面积　　　　　个平方单位 …… …… ①1=12； ②1+3=22； ③1+3+5=32； ④ ； ⑤ ； 第 1 次 第 2 次 第 3 次 第 4 次 ··· ·· · ⑴ ⑵ ⑶ 14Ìâ 13、图（1）是一个水平摆放的小正方体木块，图（2）、（3）是由这样的小正方体木块叠放而成，按照这样 的规律继续叠放下去，至第七个叠放的图形中，小正方体木块总数应是（ ） A 25 B 66 C 91 D 120 14、如图是由大小相同的小立方体木块叠入而成的几何体，图⑴中有 1 个立方体，图⑵中有 4 个立方体， 图⑶中有 9 个立方体，……按这样的规律叠放下去， 第 8 个图中小立方体个数是 . 15、图 1 是棱长为 a 的小正方体，图 2、图 3 由这样的小正方体摆放而成．按照这样的方法继续摆放，由 上而下分别叫第一层、第二层、…、第 n 层，第 n 层的小正方体的个数为 s．解答下列问题： （1）按照要求填表： （2）写出当 n=10 时，s= ． 16、如图用火柴摆去系列图案，按这种方式摆下去，当每边摆 10 根时（即 ）时，需要的火柴棒总数 为 根； 17、用火柴棒按如图的方式搭一行三角形，搭一个三角形需 3 支火柴棒，搭 2 个三角形需 5 支火柴棒，搭 n 1 2 3 4 … s 1 3 6 … 10=n (1) (2) (3) 图 1 图 2 图 3 A B C D 3 个三角形需 7 支火柴棒，照这样的规律下去，搭 n 个三角形需要 S 支火柴棒，那么用 n 的式子表示 S 的式子是 _______ （n 为正整数）． 18、如图所示，用同样规格的黑、白两色正方形瓷砖铺设矩形地面，请观察下图：则第 n 个图形中需用黑 色瓷砖 ____ 块．(用含 n 的代数式表示) 19 题图 19、如图，用同样规格的黑白两种正方形瓷砖铺设正方形地面，观察图形并猜想填空：当黑色瓷砖为 20 块 时，白色瓷砖为 块；当白色瓷砖为 n2(n 为正整数)块时，黑色瓷砖为 块． 20、观察下列由棱长为 1 的小立方体摆成的图形，寻找规律：如图 1 中：共有 1 个小立方体，其中 1 个看 得见，0 个看不见；如图 2 中：共有 8 个小立方体，其中 7 个看得见，1 个看不见；如图 3 中：共有 27 个 小立方体，其中有 19 个看得 8 个看不见；……，则第 6 个图中，看不见的小立方体有 个。 21、下面的图形是由边长为 l 的正方形按照某种规律排列而组成的． （1）观察图形，填写下表： 图形 ① ② ③ 正方形的个数 8 图形的周长 18 (2)推测第 n 个图形中，正方形的个数为________，周长为______________(都用含 n 的代数式表示)． 22、观察下图，我们可以发现：图⑴中有 1 个正方形；图⑵中有 5 个正方形，图⑶中共有 14 个正方形，按 照这种规律继续下去，图⑹中共有_______个正方形。 23、某正方形园地是由边长为 1 的四个小正方形组成的，现要在园地上建一个花坛（阴影部分）使花坛面 积是园地面积的一半，以下图中设计不合要求的是( ) 第 22 题图 第 23 题图 24、如下图中的四个正方形的边长均相等，其中阴影部分面积最大的图形是( ) A DCB 第 18 题 图图 25、如图，在方格纸中有四个图形<1>、<2>、<3>、<4>，其中面积相等的图形是（ ） A. <1>和<2> B. <2>和<3> C. <2>和<4> D. <1>和<4> 26、某体育馆用大小相同的长方形木块镶嵌地面，第 1 次铺 2 块，如图 1；第 2 次把第 1 次铺的完全围起 来，如图 2；第 3 次把第 2 次铺的完全围起来，如图 3；…依此方法，第 n 次铺完后，用字母 n 表示第 n 次 镶嵌所使用的木块块数为 . （n 为正整数） 27、用黑白两种颜色的正六边形地面砖按如下所示的规律，拼成若干个图案： ⑴ 第 4 个图案中有白色地面砖 块； ⑵ 第 n 个图案中有白色地面砖 块。 28、分析如下图①,②,④中阴影部分的分布规律，按此规律在图③中画出其中的阴影部分. 29、将一圆形纸片对折后再对折，得到图 2，然后沿着图中的虚线剪开，得到两部分，其中一部分展开后 的平面图形是( ) 30．如图（1），小强拿一张正方形的纸，沿虚线对折一次得图（2），再对折一次得图（3），然后用剪刀沿 A B C D 图3 图 2 图（3）中的虚线剪去一个角，再打开后的形状是（ ） （A）　 （B） （C） （D） 图１ C D EB A 图（２） 31、 用一条宽相等的足够长的纸条，打一个结，如图（１）所示，然后轻轻拉紧、压平就可以得到如图 （２）所示的正五边形ＡＢＣＤＥ，其中∠ＢＡＣ＝　　　　度. 32、如图，一张长方形纸沿 AB 对折，以 AB 中点 O 为顶点将平角五等分，并沿五等分的折线折叠，再沿 CD 剪开，使展开后为正五角星（正五边形对角线所构成的图形）.则∠OCD 等于（　　） A．108° B．144° C．126° D．129° 33、如图，把一个正方形三次对折后沿虚线剪下则得到的图形是（ ） A B C D 第 35 题图 34、将一张长方形的纸对折，如图 5 所示可得到一条折痕（图中虚线）. 继续对折，对折时每次折痕与上 次的折痕保持平行，连续对折三次后，可以得到 7 条折痕，那么对折四次可以得到 条折痕 .如 果对折 n 次，可以得到 _____________条折痕 。 35、观察图形：图中是边长为 1，2，3 …的正方形：当边长 ＝1 时，正方形被分成 2 个大小相等的小等 腰直角三角形；当边长 ＝2 时，正方形被分成 8 个大小相等的小等腰直角三角形；当边长 ＝3 时，正方 形被分成 18 个大小相等的小等腰直角三角形；以此类推：当边长为 时，正方形被分成大小相等的小等腰 直角三角形的个数是 。 36、水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如右图,是一个正 方体的平面展开图,若图中的“似”表示正方体的前面, “锦”表示右面, “程”表示下面.则“祝”、 “你”、“前”分别表示正方体的___________________. 右折 右下方折 _沿虚线剪开 n n n n 37、如图是一块长方形 ABCD 的场地，长 AB=102m，宽 AD=51m，从 A、B 两处入口的中路宽都为 1m，两小路汇 合处路宽为 2m，其余部分种植草坪，则草坪面积为（ ） （A）5050m2 （B）4900m2 （Ｃ）5000m2（Ｄ）4998m2 38、读一读，想一想，做一做： 国际象棋、中国象棋和围棋号称为世界三大棋种.国际象棋中的“皇后”的威力可比中国象棋中的“车” 大得多：“皇后”不仅能控制她所在的行与列中的每一个小方格，而且还能控制“斜”方向的两条直线上 的每一个小方格.如图甲是一个 4×4 的小方格棋盘，图中的“皇后 Q”能控制图中虚线所经过的每一个小 方格. ① 在如图乙的小方格棋盘中有一“皇后 Q”，她所在的位置可用“(2，3)”来表示，请说明“皇后 Q”所 在的位置“(2，3)”的意义，并用这种表示法分别写出棋盘中不能被该“皇后 Q”所控制的四个位置. ②如图丙也是一个 4×4 的小方格棋盘，请在这个棋盘中放入四个“皇后 Q”，使这四个“皇后Q”之间互 不受对方控制（在图丙中的某四个小方格中标出字母 Q 即可）. 1 2 3 4 1 2 3 4 Q 甲 1 2 3 4 1 2 3 4 Q 行 列 乙 1 2 3 4 1 2 3 4 丙 程前你 祝 似 锦 A S A D S A C S A B S A 参考答案 1、13 2、100 3、C 4、179 5、 3（n+1）-3+n（n+1）或（n+1） 2+2n-1 6、（1）18、22 （2）4n+2 7、27 8、31，n2-n-1 9、80 10、1+3+5+7=42；1+3+5+7+9=52；1+3+5+……+2n-1=n2 11、 4n 12、90 13、C 14、64 5、（1）10 （2）1+2+3+……+n=n(n+1)/2 16、 165 17、s=2n+1 18、4n+6 19、16，4n+4 20、125 21、（1）13、18；28、38； （2）5n+3,10n+8 22 、91 23、B 24、B 25、A 26、8n-6 27、（1）18 ； （2）4n+2 28、 29、C 30、C 31、 36 32、A 33、C 34、15 ；2n-1 35、 2n2 36、后面、上面、左面 37、C 38、（1） （1，1），（3，1），（4，2），（4，4）；（2）