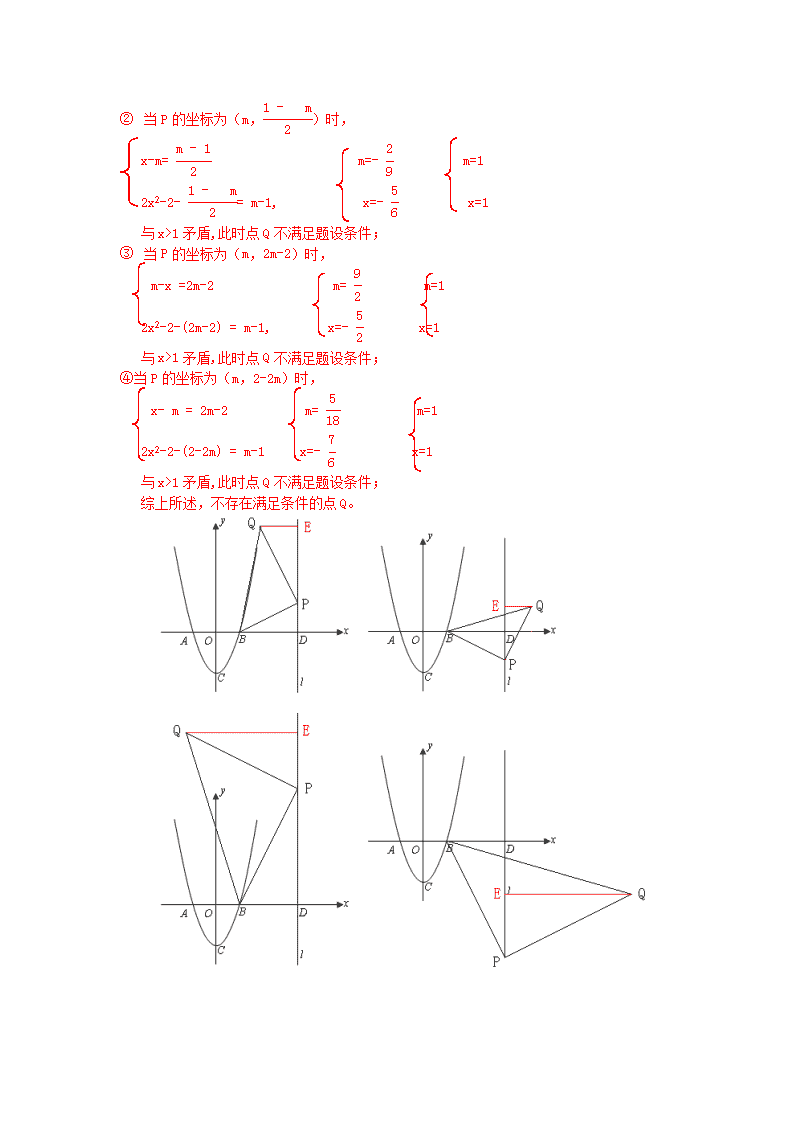中考二次函数压轴题精选含答案 43页

‎2013年中考二次函数压轴题精选 ‎1、（绵阳市2013年）A B C D O x y l 如图，二次函数y=ax2+bx+c的图象的顶点C的坐标为（0，-2），交x轴于A、B两点，其中A（-1，0），直线l：x=m（m＞1）与x轴交于D。‎ ‎（1）求二次函数的解析式和B的坐标；‎ ‎（2）在直线l上找点P（P在第一象限），使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似，求点P的坐标（用含m的代数式表示）；‎ ‎（3）在（2）成立的条件下，在抛物线上是否存在第一象限内的点Q，使△BPQ是以P为直角顶点的等腰直角三角形？如果存在，请求出点Q的坐标；如果不存在，请说明理由。‎ 解：（1）①二次函数y=ax2+bx+c图象的顶点C的坐标为（0，-2），c = -2 , - , b=0 ,‎ 点A(-1,0)、点B是二次函数y=ax2-2 的图象与x轴的交点，a-2=0,a=2. 二次函数的解析式为y=2x2-2；‎ ‎②点B与点A(-1,0)关于直线x=0对称，点B的坐标为（1，0）；‎ ‎（2）∠BOC=∠PDB=90º，点P在直线x=m上，‎ 设点P的坐标为（m,p）, OB=1， OC=2， DB= m-1 , DP=|p| ，‎ ‎①当△BOC∽△PDB时，,,p= 或p = ,‎ 点P的坐标为（m，）或（m，）；‎ ‎②当△BOC∽△BDP时， ，，p=2m-2或p=2-2m,‎ 点P的坐标为（m，2m-2）或（m，2-2m）；‎ 综上所述点P的坐标为（m，）、（m，）、（m，2m-2）或（m，2-2m）；‎ ‎（3）不存在满足条件的点Q。‎ 点Q在第一象限内的抛物线y=2x2-2上，‎ 令点Q的坐标为（x, 2x2-2），x>1, 过点Q作QE⊥直线l , ‎ 垂足为E，△BPQ为等腰直角三角形，PB=PQ，∠PEQ=∠PDB，‎ ‎∠EPQ=∠DBP，△PEQ≌△BDP，QE=PD，PE=BD，‎ ① 当P的坐标为（m，）时，‎ m-x = ， m=0 m=1‎ ‎ 2x2-2- = m-1, x= x=1 ‎ 与x>1矛盾,此时点Q不满足题设条件；‎ ① 当P的坐标为（m，）时，‎ x-m= m=- m=1‎ ‎2x2-2- = m-1, x=- x=1 ‎ 与x>1矛盾,此时点Q不满足题设条件；‎ ② 当P的坐标为（m，2m-2）时，‎ m-x =2m-2 m= m=1‎ ‎2x2-2-(2m-2) = m-1, x=- x=1‎ 与x>1矛盾,此时点Q不满足题设条件；‎ ‎④当P的坐标为（m，2-2m）时，‎ x- m = 2m-2 m= m=1‎ ‎2x2-2-(2-2m) = m-1 x=- x=1‎ 与x>1矛盾,此时点Q不满足题设条件；‎ 综上所述，不存在满足条件的点Q。‎ ‎2、（2013•昆明压轴题）如图，矩形OABC在平面直角坐标系xOy中，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=4，OC=3，若抛物线的顶点在BC边上，且抛物线经过O，A两点，直线AC交抛物线于点D．‎ ‎（1）求抛物线的解析式；‎ ‎（2）求点D的坐标；‎ ‎（3）若点M在抛物线上，点N在x轴上，是否存在以A，D，M，N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．‎ 解：（1）设抛物线顶点为E，根据题意OA=4，OC=3，得：E（2，3），‎ 设抛物线解析式为y=a（x﹣2）2+3，‎ 将A（4，0）坐标代入得：0=4a+3，即a=﹣，‎ 则抛物线解析式为y=﹣（x﹣2）2+3=﹣x2+3x；‎ ‎（2）设直线AC解析式为y=kx+b（k≠0），‎ 将A（4，0）与C（0，3）代入得：，‎ 解得：，‎ 故直线AC解析式为y=﹣x+3，‎ 与抛物线解析式联立得：，‎ 解得：或，‎ 则点D坐标为（1，）；‎ ‎（3）存在，分两种情况考虑：‎ ‎①当点M在x轴上方时，如答图1所示：‎ 四边形ADMN为平行四边形，DM∥AN，DM=AN，‎ 由对称性得到M（3，），即DM=2，故AN=2，‎ ‎∴N1（2，0），N2（6，0）；‎ ‎②当点M在x轴下方时，如答图2所示：‎ 过点D作DQ⊥x轴于点Q，过点M作MP⊥x轴于点P，可得△ADQ≌△NMP，‎ ‎∴MP=DQ=，NP=AQ=3，‎ 将yM=﹣代入抛物线解析式得：﹣=﹣x2+3x，‎ 解得：xM=2﹣或xM=2+，‎ ‎∴xN=xM﹣3=﹣﹣1或﹣1，‎ ‎∴N3（﹣﹣1，0），N4（﹣1，0）．‎ 综上所述，满足条件的点N有四个：N1（2，0），N2（6，0），N3（﹣﹣1，0），N4（﹣1，0）．‎ ‎3、（2013陕西）‎（第24题图）‎ y ‎-1‎ O x ‎2‎ ‎-1‎ ‎1‎ ‎1‎ ‎2‎ ‎3‎ ‎-2‎ ‎3‎ 在平面直角坐标系中，一个二次函灵敏的图象经过点A（1，0）、B（3，0）两点．‎ ‎（1）写出这个二次函数的对称轴； ‎ ‎（2）设这个二次函数的顶点为D，与y轴交于点C，‎ 它的对称轴与x轴交于点E，连接AD、DE和DB，‎ 当△AOC与△DEB相似时，求这个二次函数的表达式。‎ 解：（1）对称轴为直线：x=2。‎ ‎（2）∵A（1，0）、B（3，0），所以设即 当x=0时，y=3a，当x=2时，y=‎ ‎∴C（0，3a），D(2,-a) ∴OC=|3a|,‎ ‎∵A（1，0）、E（2，0），‎ ‎∴OA=1,EB=1,DE=}-a|=|a|‎ 在△AOC与△DEB中，‎ ‎∵∠AOC=∠DEB=90°‎ ‎∴当时，△AOC∽△DEB ‎∴时，解得或 当时，△AOC∽△BED ‎∴时，此方程无解，‎ 综上所得：所求二次函数的表达式为：‎ 或 ‎4、（2013年潍坊市压轴题）如图，抛物线关于直线对称，与坐标轴交于三点，且,点在抛物线上，直线是一次函数的图象，点是坐标原点.‎ ‎（1）求抛物线的解析式；‎ ‎（2）若直线平分四边形的面积，求的值.‎ ‎（3）把抛物线向左平移1个单位，再向下平移2个单位，所得抛物线与直线交于两点，问在轴正半轴上是否存在一定点，使得不论取何值，直线与总是关于轴对称？若存在，求出点坐标；若不存在，请说明理由.‎ 答案：（1）因为抛物线关于直线x=1对称，AB=4，所以A(-1，0),B(3，0),‎ 由点D(2，1.5)在抛物线上，所以，所以3a+3b=1.5,即a+b=0.5,‎ 又，即b=-2a,代入上式解得a=-0.5,b=1,从而c=1.5,所以.‎ ‎（2）由（1）知，令x=0,得c(0,1.5),所以CD//AB,‎ 令kx-2=1.5,得l与CD的交点F()，‎ 令kx-2=0，得l与x轴的交点E()，‎ 根据S四边形OEFC=S四边形EBDF得：OE+CF=DF+BE,‎ 即：‎ ‎（3）由（1）知 所以把抛物线向左平移1个单位，再向下平移2个单位，所得抛物线的解析式为 假设在y轴上存在一点P(0，t)，t＞0，使直线PM与PN关于y轴对称，过点M、N分别向y轴作垂线MM1、NN1，垂足分别为M1、N1，因为∠MPO=∠NPO,所以Rt△MPM1∽Rt△NPN1,‎ 所以,………………(1)‎ 不妨设M(xM,yM)在点N(xN,yN)的左侧，因为P点在y轴正半轴上，‎ 则（1）式变为,又yM =k xM-2, yN=k xN-2, ‎ 所以（t+2）(xM +xN)=2k xM xN,……(2)‎ 把y=kx-2(k≠0)代入中，整理得x2+2kx-4=0,‎ 所以xM +xN=-2k, xM xN=-4,代入（2）得t=2,符合条件，‎ 故在y轴上存在一点P（0,2），使直线PM与PN总是关于y轴对称.‎ ‎5、（2013•新疆压轴题）如图，已知抛物线y=ax2+bx+3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在（1）中抛物线的对称轴上是否存在点D，使△BCD的周长最小？若存在，求出点D的坐标，若不存在，请说明理由；‎ ‎（3）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标．‎ 解：（1）∵抛物线y=ax2+bx+3经过点A（1，0），点C（4，3），‎ ‎∴，解得，‎ 所以，抛物线的解析式为y=x2﹣4x+3；‎ ‎（2）∵点A、B关于对称轴对称，‎ ‎∴点D为AC与对称轴的交点时△BCD的周长最小，‎ 设直线AC的解析式为y=kx+b（k≠0），‎ 则，‎ 解得，‎ 所以，直线AC的解析式为y=x﹣1，‎ ‎∵y=x2﹣4x+3=（x﹣2）2﹣1，‎ ‎∴抛物线的对称轴为直线x=2，‎ 当x=2时，y=2﹣1=1，‎ ‎∴抛物线对称轴上存在点D（2，1），使△BCD的周长最小；‎ ‎（3）如图，设过点E与直线AC平行线的直线为y=x+m，‎ 联立， ‎ 消掉y得，x2﹣5x+3﹣m=0，‎ ‎△=（﹣5）2﹣4×1×（3﹣m）=0，‎ 即m=﹣时，点E到AC的距离最大，△ACE的面积最大，‎ 此时x=，y=﹣，‎ ‎∴点E的坐标为（，﹣），‎ 设过点E的直线与x轴交点为F，则F（，0），‎ ‎∴AF=﹣1=，‎ ‎∵直线AC的解析式为y=x﹣1，‎ ‎∴∠CAB=45°，‎ ‎∴点F到AC的距离为×=，‎ 又∵AC==3，‎ ‎∴△ACE的最大面积=×3×=，此时E点坐标为（，﹣）．‎ ‎6、（2013凉山州压轴题）如图，抛物线y=ax2﹣2ax+c（a≠0）交x轴于A、B两点，A点坐标为（3，0），与y轴交于点C（0，4），以OC、OA为边作矩形OADC交抛物线于点G．‎ ‎（1）求抛物线的解析式；‎ ‎（2）抛物线的对称轴l在边OA（不包括O、A两点）‎ 上平行移动，分别交x轴于点E，交CD于点F，交 AC于点M，交抛物线于点P，若点M的横坐标为m，‎ 请用含m的代数式表示PM的长；‎ ‎（3）在（2）的条件下，连结PC，则在CD上方的抛 物线部分是否存在这样的点P，使得以P、C、F为顶 点的三角形和△AEM相似？若存在，求出此时m的 值，并直接判断△PCM的形状；若不存在，请说明理由．‎ 解答：解：（1）∵抛物线y=ax2﹣2ax+c（a≠0）经过点A（3，0），点C（0，4），‎ ‎∴，解得，‎ ‎∴抛物线的解析式为y=﹣x2+x+4；‎ ‎（2）设直线AC的解析式为y=kx+b，‎ ‎∵A（3，0），点C（0，4），‎ ‎∴，解得，‎ ‎∴直线AC的解析式为y=﹣x+4．‎ ‎∵点M的横坐标为m，点M在AC上，‎ ‎∴M点的坐标为（m，﹣ m+4），‎ ‎∵点P的横坐标为m，点P在抛物线y=﹣x2+x+4上，‎ ‎∴点P的坐标为（m，﹣ m2+m+4），‎ ‎∴PM=PE﹣ME=（﹣m2+m+4）﹣（﹣m+4）=﹣m2+4m，‎ 即PM=﹣m2+4m（0＜m＜3）；‎ ‎（3）在（2）的条件下，连结PC，在CD上方的抛物线部分存在这样的点P，使得以P、C、F为顶点的三角形和△AEM相似．理由如下：由题意，可得AE=3﹣m，EM=﹣m+4，CF=m，PF=﹣m2+m+4﹣4=﹣m2+m．‎ 若以P、C、F为顶点的三角形和△AEM相似，分两种情况：①若△PFC∽△AEM，则PF：AE=FC：EM，‎ 即（﹣m2+m）：（3﹣m）=m：（﹣ m+4），‎ ‎∵m≠0且m≠3，‎ ‎∴m=．‎ ‎∵△PFC∽△AEM，∴∠PCF=∠AME，‎ ‎∵∠AME=∠CMF，∴∠PCF=∠CMF．‎ 在直角△CMF中，∵∠CMF+∠MCF=90°，‎ ‎∴∠PCF+∠MCF=90°，即∠PCM=90°，‎ ‎∴△PCM为直角三角形；‎ ‎②若△CFP∽△AEM，则CF：AE=PF：EM，‎ 即m：（3﹣m）=（﹣m2+m）：（﹣m+4），‎ ‎∵m≠0且m≠3，‎ ‎∴m=1．‎ ‎∵△CFP∽△AEM，∴∠CPF=∠AME，‎ ‎∵∠AME=∠CMF，∴∠CPF=∠CMF．‎ ‎∴CP=CM，‎ ‎∴△PCM为等腰三角形．‎ 综上所述，存在这样的点P使△PFC与△AEM相似．此时m的值为或1，△PCM为直角三角形或等腰三角形．‎ ‎7、（2013•曲靖压轴题）如图，在平面直角坐标系xOy中，直线y=x+4与坐标轴分别交于A、B两点，过A、B两点的抛物线为y=﹣x2+bx+c．点D为线段AB上一动点，过点D作CD⊥x轴于点C，交抛物线于点E．‎ ‎（1）求抛物线的解析式．‎ ‎（2）当DE=4时，求四边形CAEB的面积．‎ ‎（3）连接BE，是否存在点D，使得△DBE和△DAC相似？若存在，求此点D坐标；若不存在，说明理由．‎ 解：（1）在直线解析式y=x+4中，令x=0，得y=4；令y=0，得x=﹣4，‎ ‎∴A（﹣4，0），B（0，4）．‎ ‎∵点A（﹣4，0），B（0，4）在抛物线y=﹣x2+bx+c上，‎ ‎∴，‎ 解得：b=﹣3，c=4，‎ ‎∴抛物线的解析式为：y=﹣x2﹣3x+4．‎ ‎（2）设点C坐标为（m，0）（m＜0），则OC=﹣m，AC=4+m．‎ ‎∵OA=OB=4，∴∠BAC=45°，‎ ‎∴△ACD为等腰直角三角形，∴CD=AC=4+m，‎ ‎∴CE=CD+DE=4+m+4=8+m，‎ ‎∴点E坐标为（m，8+m）．‎ ‎∵点E在抛物线y=﹣x2﹣3x+4上，‎ ‎∴8+m=﹣m2﹣3m+4，解得m=﹣2．‎ ‎∴C（﹣2，0），AC=OC=2，CE=6，‎ S四边形CAEB=S△ACE+S梯形OCEB﹣S△BCO=×2×6+（6+4）×2﹣×2×4=12．‎ ‎（3）设点C坐标为（m，0）（m＜0），则OC=﹣m，CD=AC=4+m，BD=OC=﹣m，则D（m，4+m）．‎ ‎∵△ACD为等腰直角三角形，△DBE和△DAC相似 ‎∴△DBE必为等腰直角三角形．‎ i）若∠BED=90°，则BE=DE，‎ ‎∵BE=OC=﹣m，‎ ‎∴DE=BE=﹣m，X Kb1. Co m ‎∴CE=4+m﹣m=4，‎ ‎∴E（m，4）．‎ ‎∵点E在抛物线y=﹣x2﹣3x+4上，‎ ‎∴4=﹣m2﹣3m+4，解得m=0（不合题意，舍去）或m=﹣3，‎ ‎∴D（﹣3，1）；‎ ii）若∠EBD=90°，则BE=BD=﹣m，‎ 在等腰直角三角形EBD中，DE=BD=﹣2m，‎ ‎∴CE=4+m﹣2m=4﹣m，‎ ‎∴E（m，4﹣m）．‎ ‎∵点E在抛物线y=﹣x2﹣3x+4上，‎ ‎∴4﹣m=﹣m2﹣3m+4，解得m=0（不合题意，舍去）或m=﹣2，‎ ‎∴D（﹣2，2）．‎ 综上所述，存在点D，使得△DBE和△DAC相似，点D的坐标为（﹣3，1）或（﹣2，2）．11、8、(2013年临沂压轴题)如图，抛物线经过三点.‎ ‎(1)求抛物线的解析式；‎ ‎(2)在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；‎ ‎(3)点M为x轴上一动点，在抛物线上是否存在一点N，使以A,C,M,N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由.‎ x y A O C B ‎（第26题图）‎ ‎ ‎ 解析：解：（1）设抛物线的解析式为 ， ‎ x y A O C B ‎（第26题图）‎ P N M H ‎ 根据题意，得，‎ 解得 ‎∴抛物线的解析式为： ‎ ‎（2）由题意知，点A关于抛物线对称轴的对称点为点B,连接BC交抛物线的对称轴于点P，则P点 即为所求.‎ 设直线BC的解析式为，由题意，得解得 ‎ ‎∴直线BC的解析式为 ‎ ‎∵抛物线的对称轴是，∴当时，‎ ‎∴点P的坐标是. ‎ ‎（3）存在 ‎ ‎(i)当存在的点N在x轴的下方时，如图所示，∵四边形ACNM是平行四边形，∴CN∥x轴，∴点C与点N关于对称轴x=2对称，∵C点的坐标为，∴点N的坐标为 ‎ ‎（II）当存在的点在x轴上方时，如图所示，作轴于点H，∵四边形是平行四边形，∴,‎ ‎∴Rt△CAO ≌Rt△,∴.‎ ‎∵点C的坐标为,即N点的纵坐标为，‎ ‎∴即 解得 ‎∴点的坐标为和.‎ 综上所述，满足题目条件的点N共有三个，‎ 分别为，， ‎ ‎9、（2013•宁波压轴题）如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（0，4），点B的坐标为（4，0），点C的坐标为（﹣4，0），点P在射线AB上运动，连结CP与y轴交于点D，连结BD．过P，D，B三点作⊙Q与y轴的另一个交点为E，延长DQ交⊙Q于点F，连结EF，BF．‎ ‎ （1）求直线AB的函数解析式；‎ ‎（2）当点P在线段AB（不包括A，B两点）上时．‎ ‎①求证：∠BDE=∠ADP；‎ ‎②设DE=x，DF=y．请求出y关于x的函数解析式；‎ ‎（3）请你探究：点P在运动过程中，是否存在以B，D，F为顶点的直角三角形，满足两条直角边之比为2：1？如果存在，求出此时点P的坐标：如果不存在，请说明理由．‎ 解：（1）设直线AB的函数解析式为y=kx+4，‎ 代入（4，0）得：4k+4=0，‎ 解得：k=﹣1，‎ 则直线AB的函数解析式为y=﹣x+4；‎ ‎（2）①由已知得：‎ OB=OC，∠BOD=∠COD=90°，‎ 又∵OD=OD，‎ ‎∴△BOD≌△COD，‎ ‎∴∠BOD=∠CDO，‎ ‎∵∠CDO=∠ADP，‎ ‎∴∠BDE=∠ADP，‎ ‎②连结PE，‎ ‎∵∠ADP是△DPE的一个外角，∴∠ADP=∠DEP+∠DPE，‎ ‎∵∠BDE是△ABD的一个外角，∴∠BDE=∠ABD+∠OAB，‎ ‎∵∠ADP=∠BDE，∠DEP=∠ABD，∴∠DPE=∠OAB，‎ ‎∵OA=OB=4，∠AOB=90°，∴∠OAB=45°，∴∠DPE=45°，∴∠DFE=∠DPE=45°，‎ ‎∵DF是⊙Q的直径，∴∠DEF=90°，∴△DEF是等腰直角三角形，‎ ‎∴DF=DE，即y=x；‎ ‎（3）当BD：BF=2：1时，‎ 过点F作FH⊥OB于点H，‎ ‎∵∠DBO+∠OBF=90°，∠OBF+∠BFH=90°，∴∠DBO=∠BFH，‎ 又∵∠DOB=∠BHF=90°，∴△BOD∽△FHB，∴===2，∴FH=2，OD=2BH，‎ ‎∵∠FHO=∠EOH=∠OEF=90°，∴四边形OEFH是矩形，‎ ‎∴OE=FH=2，∴EF=OH=4﹣OD，‎ ‎∵DE=EF，∴2+OD=4﹣OD，‎ 解得：OD=，∴点D的坐标为（0，），‎ ‎∴直线CD的解析式为y=x+，由得：，‎ 则点P的坐标为（2，2）；当=时，‎ 连结EB，同（2）①可得：∠ADB=∠EDP，‎ 而∠ADB=∠DEB+∠DBE，∠EDP=∠DAP+∠DPA，‎ ‎∵∠DEP=∠DPA，∴∠DBE=∠DAP=45°，∴△DEF是等腰直角三角形，‎ 过点F作FG⊥OB于点G，‎ 同理可得：△BOD∽△FGB，∴===，‎ ‎∴FG=8，OD=BG，‎ ‎∵∠FGO=∠GOE=∠OEF=90°，∴四边形OEFG是矩形，‎ ‎∴OE=FG=8，∴EF=OG=4+2OD，‎ ‎∵DE=EF，∴8﹣OD=4+2OD，OD=，‎ ‎∴点D的坐标为（0，﹣），‎ 直线CD的解析式为：y=﹣x﹣，‎ 由得：，‎ ‎∴点P的坐标为（8，﹣4），‎ 综上所述，点P的坐标为（2，2）或（8，﹣4）．‎ ‎10、（2013四川宜宾压轴题）如图，抛物线y1=x2﹣1交x轴的正半轴于点A，交y轴于点B，将此抛物线向右平移4个单位得抛物线y2，两条抛物线相交于点C．‎ ‎（1）请直接写出抛物线y2的解析式；‎ ‎（2）若点P是x轴上一动点，且满足∠CPA=∠OBA，求出所有满足条件的P点坐标；‎ ‎（3）在第四象限内抛物线y2上，是否存在点Q，使得△QOC中OC边上的高h有最大值？若存在，请求出点Q的坐标及h的最大值；若不存在，请说明理由．‎ 解：（1）抛物线y1=x2﹣1向右平移4个单位的顶点坐标为（4，﹣1），‎ 所以，抛物线y2的解析式为y2=（x﹣4）2﹣1；‎ ‎（2）x=0时，y=﹣1，‎ y=0时，x2﹣1=0，解得x1=1，x2=﹣1，‎ 所以，点A（1，0），B（0，﹣1），‎ ‎∴∠OBA=45°，‎ 联立，解得， ∴点C的坐标为（2，3），‎ ‎∵∠CPA=∠OBA，∴点P在点A的左边时，坐标为（﹣1，0），‎ 在点A的右边时，坐标为（5，0），‎ 所以，点P的坐标为（﹣1，0）或（5，0）；‎ ‎（3）存在．‎ ‎∵点C（2，3），‎ ‎∴直线OC的解析式为y=x，‎ 设与OC平行的直线y=x+b，联立，‎ 消掉y得，2x2﹣19x+30﹣2b=0，‎ 当△=0，方程有两个相等的实数根时，△QOC中OC边上的高h有最大值，‎ 此时x1=x2=×（﹣）=，‎ 此时y=（﹣4）2﹣1=﹣，‎ ‎∴存在第四象限的点Q（，﹣），使得△QOC中OC边上的高h有最大值，‎ 此时△=192﹣4×2×（30﹣2b）=0 解得b=﹣，‎ ‎∴过点Q与OC平行的直线解析式为y=x﹣，‎ 令y=0，则x﹣=0，解得x=，‎ 设直线与x轴的交点为E，则E（，0），‎ 过点C作CD⊥x轴于D，根据勾股定理，OC==，‎ 则sin∠COD==，‎ 解得h最大=×=．‎ ‎11、（2013•广安压轴题）如图，在平面直角坐标系xOy中，抛物线y=ax2+bx+c经过A、B、C三点，已知点A（﹣3，0），B（0，3），C（1，0）．‎ ‎（1）求此抛物线的解析式．‎ ‎（2）点P是直线AB上方的抛物线上一动点，（不与点A、B重合），过点P作x轴的垂线，垂足为F，交直线AB于点E，作PD⊥AB于点D．‎ ‎①动点P在什么位置时，△PDE的周长最大，求出此时P点的坐标；‎ ‎②连接PA，以AP为边作图示一侧的正方形APMN，随着点P的运动，正方形的大小、位置也随之改变．当顶点M或N恰好落在抛物线对称轴上时，求出对应的P点的坐标．（结果保留根号）‎ 解：（1）∵抛物线y=ax2+bx+c经过点A（﹣3，0），B（0，3），C（1，0），‎ ‎∴，解得，所以，抛物线的解析式为y=﹣x2﹣2x+3；‎ ‎（2）①∵A（﹣3，0），B（0，3），∴OA=OB=3，‎ ‎∴△AOB是等腰直角三角形，∴∠BAO=45°，‎ ‎∵PF⊥x轴，∴∠AEF=90°﹣45°=45°，‎ 又∵PD⊥AB，∴△PDE是等腰直角三角形，∴PD越大，△PDE的周长越大，‎ 易得直线AB的解析式为y=x+3，‎ 设与AB平行的直线解析式为y=x+m，联立，‎ 消掉y得，x2+3x+m﹣3=0，‎ 当△=32﹣4×1×（m﹣3）=0，‎ 即m=时，直线与抛物线只有一个交点，PD最长，‎ 此时x=﹣，y=﹣+=，‎ ‎∴点P（﹣，）时，△PDE的周长最大；‎ ‎②抛物线y=﹣x2﹣2x+3的对称轴为直线x=﹣=﹣1，‎ ‎（i）如图1，点M在对称轴上时，过点P作PQ⊥对称轴于Q，‎ 在正方形APMN中，AP=PM，∠APM=90°，‎ ‎∴∠APF+∠FPM=90°，∠QPM+∠FPM=90°，‎ ‎∴∠APF=∠QPM，‎ ‎∵在△APF和△MPQ中，，‎ ‎∴△APF≌△MPQ（AAS），‎ ‎∴PF=PQ，‎ 设点P的横坐标为n（n＜0），则PQ=﹣1﹣n，‎ 即PF=﹣1﹣n，‎ ‎∴点P的坐标为（n，﹣1﹣n），‎ ‎∵点P在抛物线y=﹣x2﹣2x+3上，‎ ‎∴﹣n2﹣2n+3=﹣1﹣n，‎ 整理得，n2+n﹣4=0，‎ 解得n1=（舍去），n2=，‎ ‎﹣1﹣n=﹣1﹣=，‎ 所以，点P的坐标为（，）；‎ ‎（ii）如图2，点N在对称轴上时，设抛物线对称轴与x轴交于点Q，‎ ‎∵∠PAF+∠FPA=90°，∠PAF+∠QAN=90°，∴∠FPA=∠QAN，‎ 又∵∠PFA=∠AQN=90°，PA=AN，∴△APF≌△NAQ，∴PF=AQ，‎ 设点P坐标为P（x，﹣x2﹣2x+3），‎ 则有﹣x2﹣2x+3=﹣1﹣（﹣3）=2，‎ 解得x=﹣1（不合题意，舍去）或x=﹣﹣1，‎ 此时点P坐标为（﹣﹣1，2）．‎ 综上所述，当顶点M恰好落在抛物线对称轴上时，点P坐标为（，），当顶点N恰好落在抛物线对称轴上时，点P的坐标为（﹣﹣1，2）．‎ ‎12、（2013•绍兴压轴题）抛物线y=（x﹣3）（x+1）与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，点D为顶点．‎ ‎（1）求点B及点D的坐标．‎ ‎（2）连结BD，CD，抛物线的对称轴与x轴交于点E．‎ ‎①若线段BD上一点P，使∠DCP=∠BDE，求点P的坐标．‎ ‎②若抛物线上一点M，作MN⊥CD，交直线CD于点N，使∠CMN=∠BDE，求点M的坐标．‎ 解：（1）∵抛物线y=（x﹣3）（x+1）与x轴交于A，B两点（点A在点B左侧），‎ ‎∴当y=0时，（x﹣3）（x+1）=0，‎ 解得x=3或﹣1，‎ ‎∴点B的坐标为（3，0）．‎ ‎∵y=（x﹣3）（x+1）=x2﹣2x﹣3=（x﹣1）2﹣4，‎ ‎∴顶点D的坐标为（1，﹣4）；‎ ‎（2）①如右图．‎ ‎∵抛物线y=（x﹣3）（x+1）=x2﹣2x﹣3与与y轴交于点C，‎ ‎∴C点坐标为（0，﹣3）．‎ ‎∵对称轴为直线x=1，‎ ‎∴点E的坐标为（1，0）．‎ 连接BC，过点C作CH⊥DE于H，则H点坐标为（1，﹣3），‎ ‎∴CH=DH=1，‎ ‎∴∠CDH=∠BCO=∠BCH=45°，‎ ‎∴CD=，CB=3，△BCD为直角三角形．‎ 分别延长PC、DC，与x轴相交于点Q，R．‎ ‎∵∠BDE=∠DCP=∠QCR，‎ ‎∠CDB=∠CDE+∠BDE=45°+∠DCP，‎ ‎∠QCO=∠RCO+∠QCR=45°+∠DCP，‎ ‎∴∠CDB=∠QCO，‎ ‎∴△BCD∽△QOC，‎ ‎∴==，‎ ‎∴OQ=3OC=9，即Q（﹣9，0）．‎ ‎∴直线CQ的解析式为y=﹣x﹣3，‎ 直线BD的解析式为y=2x﹣6．‎ 由方程组，解得．‎ ‎∴点P的坐标为（，﹣）；‎ ‎②（Ⅰ）当点M在对称轴右侧时．‎ 若点N在射线CD上，如备用图1，延长MN交y轴于点F，过点M作MG⊥y轴于点G．‎ ‎∵∠CMN=∠BDE，∠CNM=∠BED=90°，‎ ‎∴△MCN∽△DBE，‎ ‎∴==，‎ ‎∴MN=2CN．‎ 设CN=a，则MN=2a．‎ ‎∵∠CDE=∠DCF=45°，‎ ‎∴△CNF，△MGF均为等腰直角三角形，‎ ‎∴NF=CN=a，CF=a，‎ ‎∴MF=MN+NF=3a，‎ ‎∴MG=FG=a，‎ ‎∴CG=FG﹣FC=a，‎ ‎∴M（a，﹣3+a）．‎ 代入抛物线y=（x﹣3）（x+1），解得a=，‎ ‎∴M（，﹣）；‎ 若点N在射线DC上，如备用图2，MN交y轴于点F，过点M作MG⊥y轴于点G．‎ ‎∵∠CMN=∠BDE，∠CNM=∠BED=90°，‎ ‎∴△MCN∽△DBE，‎ ‎∴==，‎ ‎∴MN=2CN．‎ 设CN=a，则MN=2a．‎ ‎∵∠CDE=45°，‎ ‎∴△CNF，△MGF均为等腰直角三角形，‎ ‎∴NF=CN=a，CF=a，‎ ‎∴MF=MN﹣NF=a，‎ ‎∴MG=FG=a，‎ ‎∴CG=FG+FC=a，‎ ‎∴M（a，﹣3+a）．‎ 代入抛物线y=（x﹣3）（x+1），解得a=5，‎ ‎∴M（5，12）；‎ ‎（Ⅱ）当点M在对称轴左侧时．‎ ‎∵∠CMN=∠BDE＜45°，‎ ‎∴∠MCN＞45°，‎ 而抛物线左侧任意一点K，都有∠KCN＜45°，‎ ‎∴点M不存在．‎ 综上可知，点M坐标为（，﹣）或（5，12）．‎ ‎13、（2013•嘉兴压轴题）如图，在平面直角坐标系xOy中，抛物线y=（x﹣m）2﹣m2+m的顶点为A，与y轴的交点为B，连结AB，AC⊥AB，交y轴于点C，延长CA到点D，使AD=AC，连结BD．作AE∥x轴，DE∥y轴．‎ ‎（1）当m=2时，求点B的坐标；‎ ‎（2）求DE的长？‎ ‎（3）①设点D的坐标为（x，y），求y关于x的函数关系式？②过点D作AB的平行线，与第（3）①题确定的函数图象的另一个交点为P，当m为何值时，以，A，B，D，P为顶点的四边形是平行四边形？‎ 解：（1）当m=2时，y=（x﹣2）2+1，把x=0代入y=（x﹣2）2+1，得：y=2，‎ ‎∴点B的坐标为（0，2）．‎ ‎（2）延长EA，交y轴于点F，‎ ‎∵AD=AC，∠AFC=∠AED=90°，∠CAF=∠DAE，‎ ‎∴△AFC≌△AED，∴AF=AE，‎ ‎∵点A（m，﹣ m2+m），点B（0，m），‎ ‎∴AF=AE=|m|，BF=m﹣（﹣m2+m）=m2，‎ ‎∵∠ABF=90°﹣∠BAF=∠DAE，∠AFB=∠DEA=90°，‎ ‎∴△ABF∽△DAE，‎ ‎∴=，即：=，‎ ‎∴DE=4．‎ ‎（3）①∵点A的坐标为（m，﹣ m2+m），‎ ‎∴点D的坐标为（2m，﹣ m2+m+4），‎ ‎∴x=2m，y=﹣m2+m+4，‎ ‎∴y=﹣•++4，‎ ‎∴所求函数的解析式为：y=﹣x2+x+4，‎ ‎②作PQ⊥DE于点Q，则△DPQ≌△BAF，‎ ‎（Ⅰ）当四边形ABDP为平行四边形时（如图1），‎ 点P的横坐标为3m，‎ 点P的纵坐标为：（﹣ m2+m+4）﹣（m2）=﹣m2+m+4，‎ 把P（3m，﹣ m2+m+4）的坐标代入y=﹣x2+x+4得：‎ ‎﹣m2+m+4=﹣×（3m）2+×（3m）+4，‎ 解得：m=0（此时A，B，D，P在同一直线上，舍去）或m=8．‎ ‎（Ⅱ）当四边形ABDP为平行四边形时（如图2），‎ 点P的横坐标为m，‎ 点P的纵坐标为：（﹣ m2+m+4）+（m2）=m+4，‎ 把P（m，m+4）的坐标代入y=﹣x2+x+4得：‎ m+4=﹣m2+m+4，‎ 解得：m=0（此时A，B，D，P在同一直线上，舍去）或m=﹣8，‎ 综上所述：m的值为8或﹣8．‎ ‎14、（2013菏泽压轴题）如图，三角形ABC是以BC为底边的等腰三角形，点A、C分别是一次函数y=x+3的图象与y轴的交点，点B在二次函数的图象上，且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形．‎ ‎（1）试求b，c的值，并写出该二次函数表达式；‎ ‎（2）动点P从A到D，同时动点Q从C到A都以每秒1个单位的速度运动，问：①当P运动到何处时，有PQ⊥AC？‎ ‎②当P运动到何处时，四边形PDCQ的面积最小？此时四边形PDCQ的面积是多少？‎ 解：（1）由y=﹣x+3，‎ 令x=0，得y=3，所以点A（0，3）；‎ 令y=0，得x=4，所以点C（4，0），‎ ‎∵△ABC是以BC为底边的等腰三角形，∴B点坐标为（﹣4，0），‎ 又∵四边形ABCD是平行四边形，∴D点坐标为（8，3），‎ 将点B（﹣4，0）、点D（8，3）代入二次函数y=x2+bx+c，可得，‎ 解得：，‎ 故该二次函数解析式为：y=x2﹣x﹣3．‎ ‎（2）①设点P运动了t秒时，PQ⊥AC，此时AP=t，CQ=t，AQ=5﹣t，‎ ‎∵PQ⊥AC，∴△APQ∽△CAO，∴=，即=，解得：t=．‎ 即当点P运动到距离A点个单位长度处，有PQ⊥AC．‎ ‎②∵S四边形PDCQ+S△APQ=S△ACD，且S△ACD=×8×3=12，‎ ‎∴当△APQ的面积最大时，四边形PDCQ的面积最小，‎ 当动点P运动t秒时，AP=t，CQ=t，AQ=5﹣t，‎ 设△APQ底边AP上的高为h，作QH⊥AD于点H，由△AQH∽CAO可得： =，‎ 解得：h=（5﹣t），‎ ‎∴S△APQ=t×（5﹣t）=（﹣t2+5t）=﹣（t﹣）2+，‎ ‎∴当t=时，S△APQ达到最大值，此时S四边形PDCQ=12﹣=，‎ 故当点P运动到距离点A个单位处时，四边形PDCQ面积最小，最小值为．‎ ‎15、（2013•包头压轴题）已知抛物线y=x2﹣3x﹣的顶点为点D，并与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C．‎ ‎（1）求点A、B、C、D的坐标；‎ ‎（2）在y轴的正半轴上是否存在点P，使以点P、O、A为顶点的三角形与△AOC相似？若存在，求出点P的坐标；若不存在，请说明理由；‎ ‎（3）取点E（﹣，0）和点F（0，﹣），直线l经过E、F两点，点G是线段BD的中点．‎ ‎①点G是否在直线l上，请说明理由；‎ ‎②在抛物线上是否存在点M，使点M关于直线l的对称点在x轴上？若存在，求出点M的坐标；若不存在，请说明理由．‎ 解：（1）令y=0，则x2﹣3x﹣=0，整理得，4x2﹣12x﹣7=0，‎ 解得x1=﹣，x2=，‎ 所以，A（﹣，0），B（，0），‎ 令x=0，则y=﹣，‎ 所以，C（0，﹣），‎ ‎∵﹣=﹣=，==﹣4，‎ ‎∴顶点D（，﹣4）；‎ ‎（2）在y轴正半轴上存在符合条件的点P，设点P的坐标为（0，y），‎ ‎∵A（﹣，0），C（0，﹣），‎ ‎∴OA=，OC=，OP=y，‎ ‎①若OA和OA是对应边，则△AOP∽△AOC，‎ ‎∴=，y=OC=，此时点P（0，），‎ ‎②若OA和OC是对应边，则△POA∽△AOC，‎ ‎∴=，即=，解得y=，此时点P（0，），‎ 所以，符合条件的点P有两个，P（0，）或（0，）；‎ ‎（3）①设直线l的解析式为y=kx+b（k≠0），‎ ‎∵直线l经过点E（﹣，0）和点F（0，﹣），‎ ‎∴，解得，所以，直线l的解析式为y=﹣x﹣，‎ ‎∵B（，0），D（，﹣4），‎ ‎（+）=，[0+（﹣4）]=﹣2，∴线段BD的中点G的坐标为（，﹣2），‎ 当x=时，y=﹣×﹣=﹣2，‎ 所以，点G在直线l上；‎ ‎②在抛物线上存在符合条件的点M．‎ 设抛物线的对称轴与x轴交点为H，则点H的坐标为（，0），‎ ‎∵E（﹣，0）、F（0，﹣），B（，0）、D（，﹣4），‎ ‎∴OE=，OF=，HD=4，HB=﹣=2，‎ ‎∵==，∠OEF=∠HDB，∴△OEF∽△HDB，∴∠OFE=∠HBD，‎ ‎∵∠OEF+∠OFE=90°，∴∠OEF+∠HBD=90°，‎ ‎∴∠EGB=180°﹣（∠OEF+∠HBD）=180°﹣90°=90°，‎ ‎∴直线l是线段BD的垂直平分线，‎ ‎∴点D关于直线l的对称点就是点B，‎ ‎∴点M就是直线DE与抛物线的交点，‎ 设直线DE的解析式为y=mx+n，‎ ‎∵D（，﹣4），（﹣，0），∴，解得，‎ 所以，直线DE的解析式为y=﹣x﹣2，‎ 联立，解得，，‎ ‎∴符合条件的点M有两个，是（，﹣4）或（，﹣）．‎ ‎16、（2013•株洲压轴题）已知抛物线C1的顶点为P（1，0），且过点（0，）．将抛物线C1向下平移h个单位（h＞0）得到抛物线C2．一条平行于x轴的直线与两条抛物线交于A、B、C、D四点（如图），且点A、C关于y轴对称，直线AB与x轴的距离是m2（m＞0）．‎ ‎（1）求抛物线C1的解析式的一般形式；‎ ‎（2）当m=2时，求h的值；‎ ‎（3）若抛物线C1的对称轴与直线AB交于点E，与抛物线C2交于点F．求证：tan∠EDF﹣tan∠ECP=．‎ ‎（1）解：设抛物线C1的顶点式形式y=a（x﹣1）2，（a≠0），‎ ‎∵抛物线过点（0，），∴a（0﹣1）2=，解得a=，‎ ‎∴抛物线C1的解析式为y=（x﹣1）2，一般形式为y=x2﹣x+；‎ ‎（2）解：当m=2时，m2=4，‎ ‎∵BC∥x轴，∴点B、C的纵坐标为4，∴（x﹣1）2=4，‎ 解得x1=5，x2=﹣3，∴点B（﹣3，4），C（5，4），‎ ‎∵点A、C关于y轴对称，∴点A的坐标为（﹣5，4），‎ 设抛物线C2的解析式为y=（x﹣1）2﹣h，‎ 则（﹣5﹣1）2﹣h=4，解得h=5；‎ ‎（3）证明：∵直线AB与x轴的距离是m2，‎ ‎∴点B、C的纵坐标为m2，∴（x﹣1）2=m2，‎ 解得x1=1+2m，x2=1﹣2m，∴点C的坐标为（1+2m，m2），‎ 又∵抛物线C1的对称轴为直线x=1，∴CE=1+2m﹣1=2m，‎ ‎∵点A、C关于y轴对称，∴点A的坐标为（﹣1﹣2m，m2），‎ ‎∴AE=ED=1﹣（﹣1﹣2m）=2+2m，‎ 设抛物线C2的解析式为y=（x﹣1）2﹣h，则（﹣1﹣2m﹣1）2﹣h=m2，‎ 解得h=2m+1，∴EF=h+m2=m2+2m+1，‎ ‎∴tan∠EDF﹣tan∠ECP=﹣=﹣=﹣=，‎ ‎∴tan∠EDF﹣tan∠ECP=．‎ ‎17、（2013•张家界压轴题）如图，抛物线y=ax2+bx+c（a≠0）的图象过点C（0，1），顶点为Q（2，3），点D在x轴正半轴上，且OD=OC．‎ ‎（1）求直线CD的解析式；‎ ‎（2）求抛物线的解析式；‎ ‎（3）将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E，求证：△CEQ∽△CDO；‎ ‎（4）在（3）的条件下，若点P是线段QE上的动点，点F是线段OD上的动点，问：在P点和F点移动过程中，△PCF的周长是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．‎ 解：（1）∵C（0，1），OD=OC，∴D点坐标为（1，0）．‎ 设直线CD的解析式为y=kx+b（k≠0），‎ 将C（0，1），D（1，0）代入得：，‎ 解得：b=1，k=﹣1，‎ ‎∴直线CD的解析式为：y=﹣x+1．‎ ‎（2）设抛物线的解析式为y=a（x﹣2）2+3，‎ 将C（0，1）代入得：1=a×（﹣2）2+3，解得a=．‎ ‎∴y=（x﹣2）2+3=x2+2x+1．‎ ‎（3）证明：由题意可知，∠ECD=45°，‎ ‎∵OC=OD，且OC⊥OD，∴△OCD为等腰直角三角形，∠ODC=45°，‎ ‎∴∠ECD=∠ODC，∴CE∥x轴，则点C、E关于对称轴（直线x=2）对称，‎ ‎∴点E的坐标为（4，1）．‎ 如答图①所示，设对称轴（直线x=2）与CE交于点F，则F（2，1），‎ ‎∴ME=CM=QM=2，∴△QME与△QMC均为等腰直角三角形，∴∠QEC=∠QCE=45°．‎ 又∵△OCD为等腰直角三角形，∴∠ODC=∠OCD=45°，‎ ‎∴∠QEC=∠QCE=∠ODC=∠OCD=45°，‎ ‎∴△CEQ∽△CDO．‎ ‎（4）存在．‎ 如答图②所示，作点C关于直线QE的对称点C′，作点C关于x轴的对称点C″，连接C′C″，交OD于点F，交QE于点P，则△PCF即为符合题意的周长最小的三角形，由轴对称的性质可知，△PCF的周长等于线段C′C″的长度．‎ ‎（证明如下：不妨在线段OD上取异于点F的任一点F′，在线段QE上取异于点P的任一点P′，连接F′C″，F′P′，P′C′．‎ 由轴对称的性质可知，△P′CF′的周长=F′C″+F′P′+P′C′；‎ 而F′C″+F′P′+P′C′是点C′，C″之间的折线段，‎ 由两点之间线段最短可知：F′C″+F′P′+P′C′＞C′C″，‎ 即△P′CF′的周长大于△PCE的周长．）‎ 如答图③所示，连接C′E，‎ ‎∵C，C′关于直线QE对称，△QCE为等腰直角三角形，‎ ‎∴△QC′E为等腰直角三角形，‎ ‎∴△CEC′为等腰直角三角形，‎ ‎∴点C′的坐标为（4，5）；‎ ‎∵C，C″关于x轴对称，∴点C″的坐标为（﹣1，0）．‎ 过点C′作C′N⊥y轴于点N，则NC′=4，NC″=4+1+1=6，‎ 在Rt△C′NC″中，由勾股定理得：C′C″===．‎ 综上所述，在P点和F点移动过程中，△PCF的周长存在最小值，最小值为．‎ ‎18、（2013•衡阳）如图，已知抛物线经过A（1，0），B（0，3）两点，对称轴是x=﹣1．‎ ‎（1）求抛物线对应的函数关系式；‎ ‎（2）动点Q从点O出发，以每秒1个单位长度的速度在线段OA上运动，同时动点M从M从O点出发以每秒3个单位长度的速度在线段OB上运动，过点Q作x轴的垂线交线段AB于点N，交抛物线于点P，设运动的时间为t秒．‎ ‎①当t为何值时，四边形OMPQ为矩形；‎ ‎②△AON能否为等腰三角形？若能，求出t的值；若不能，请说明理由．‎ 解：（1）根据题意，设抛物线的解析式为：y=a（x+1）2+k，‎ ‎∵点A（1，0），B（0，3）在抛物线上，∴，解得：a=﹣1，k=4，‎ ‎∴抛物线的解析式为：y=﹣（x+1）2+4．‎ ‎（2）①∵四边形OMPQ为矩形，‎ ‎∴OM=PQ，即3t=﹣（t+1）2+4，整理得：t2+5t﹣3=0，‎ 解得t=，由于t=＜0，故舍去，‎ ‎∴当t=秒时，四边形OMPQ为矩形；‎ ‎②Rt△AOB中，OA=1，OB=3，∴tanA=3．‎ 若△AON为等腰三角形，有三种情况：‎ ‎（I）若ON=AN，如答图1所示：‎ 过点N作ND⊥OA于点D，则D为OA中点，OD=OA=，∴t=；‎ ‎（II）若ON=OA，如答图2所示：‎ 过点N作ND⊥OA于点D，设AD=x，则ND=AD•tanA=3x，OD=OA﹣AD=1﹣x，‎ 在Rt△NOD中，由勾股定理得：OD2+ND2=ON2，‎ 即（1﹣x）2+（3x）2=12，解得x1=，x2=0（舍去），‎ ‎∴x=，OD=1﹣x=，∴t=；‎ ‎（III）若OA=AN，如答图3所示：‎ 过点N作ND⊥OA于点D，设AD=x，则ND=AD•tanA=3x，‎ 在Rt△AND中，由勾股定理得：ND2+AD2=AN2，‎ 即（x）2+（3x）2=12，解得x1=，x2=﹣（舍去），‎ ‎∴OD=1﹣x=1﹣，∴t=1﹣．‎ 综上所述，当t为秒、秒，（1﹣）秒时，△AON为等腰三角形．‎ ‎19、（2013•郴州压轴题）如图，在直角梯形AOCB中，AB∥OC，∠AOC=90°，AB=1，AO=2，OC=3，以O为原点，OC、OA所在直线为轴建立坐标系．抛物线顶点为A，且经过点C．点P在线段AO上由A向点O运动，点O在线段OC上由C向点O运动，QD⊥OC交BC于点D，OD所在直线与抛物线在第一象限交于点E．‎ ‎（1）求抛物线的解析式；‎ ‎（2）点E′是E关于y轴的对称点，点Q运动到何处时，四边形OEAE′是菱形？‎ ‎（3）点P、Q分别以每秒2个单位和3个单位的速度同时出发，运动的时间为t秒，当t为何值时，PB∥OD？‎ 解：（1）∵A（0，2）为抛物线的顶点，∴设y=ax2+2，‎ ‎∵点C（3，0），在抛物线上，∴9a+2=0，解得：a=﹣，‎ ‎∴抛物线为；y=﹣x2+2；‎ ‎（2）如果四边形OEAE′是菱形，则AO与EE′互相垂直平分，‎ ‎∴EE′经过AO的中点，∴点E纵坐标为1，代入抛物线解析式得：1=﹣x2+2，‎ 解得：x=±，‎ ‎∵点E在第一象限，‎ ‎∴点E为（，1），‎ 设直线BC的解析式为y=kx+b，把B（1，2），C（3，0），代入得：，‎ 解得：，‎ ‎∴BC的解析式为：y=﹣x+3，将E点代入y=ax，可得出EO的解析式为：y=x，‎ 由，得：，‎ ‎∴Q点坐标为：（，0），‎ ‎∴当Q点坐标为（，0）时，四边形OEAE′是菱形；‎ ‎（3）法一：设t为m秒时，PB∥DO，又QD∥y轴，则有∠APB=∠AOE=∠ODQ，‎ 又∵∠BAP=∠DQO，则有△APB∽△QDO，∴=，‎ 由题意得：AB=1，AP=2m，QO=3﹣3m，‎ 又∵点D在直线y=﹣x+3上，∴DQ=3m，因此：=，解得：m=，‎ 经检验：m=是原分式方程的解，∴当t=秒时，PB∥OD．‎ ‎20、（2013•常德）如图，已知二次函数的图象过点A（0，﹣3），B（，），对称轴为直线x=﹣，点P是抛物线上的一动点，过点P分别作PM⊥x轴于点M，PN⊥y轴于点N，在四边形PMON上分别截取PC=MP，MD=OM，OE=ON，NF=NP．‎ ‎（1）求此二次函数的解析式；‎ ‎（2）求证：以C、D、E、F为顶点的四边形CDEF是平行四边形；‎ ‎（3）在抛物线上是否存在这样的点P，使四边形CDEF为矩形？若存在，请求出所有符合条件的P点坐标；若不存在，请说明理由．‎ ‎（1）解：设抛物线的解析式为：y=a（x+）2+k，‎ ‎∵点A（0，﹣3），B（，）在抛物线上，∴，‎ 解得：a=1，k=．∴抛物线的解析式为：y=（x+）2=x2+x﹣3．‎ ‎（2）证明：如右图，连接CD、DE、EF、FC．‎ ‎∵PM⊥x轴于点M，PN⊥y轴于点N，∴四边形PMON为矩形，‎ ‎∴PM=ON，PN=OM．‎ ‎∵PC=MP，OE=ON，∴PC=OE；‎ ‎∵MD=OM，NF=NP，∴MD=NF，∴PF=OD．‎ 在△PCF与△OED中，‎ ‎∴△PCF≌△OED（SAS），‎ ‎∴CF=DE．‎ 同理可证：△CDM≌△FEN，∴CD=EF．‎ ‎∵CF=DE，CD=EF，∴四边形CDEF是平行四边形．‎ ‎（3）解：假设存在这样的点P，使四边形CDEF为矩形．‎ 设矩形PMON的边长PM=ON=m，PN=OM=n，则PC=m，MC=m，MD=n，PF=n．‎ 若四边形CDEF为矩形，则∠DCF=90°，易证△PCF∽△MDC，‎ ‎∴，即，化简得：m2=n2，‎ ‎∴m=n，即矩形PMON为正方形．‎ ‎∴点P为抛物线y=x2+x﹣3与坐标象限角平分线y=x或y=﹣x的交点．‎ 联立，解得，，∴P1（，），P2（﹣，﹣）；‎ 联立，解得，，‎ ‎∴P3（﹣3，3），P4（﹣1，1）．‎ ‎∴抛物线上存在点P，使四边形CDEF为矩形．这样的点有四个，在四个坐标象限内各一个，其坐标分别为：P1（，），P2（﹣，﹣），P3（﹣3，3），P4（﹣1，1）．‎ ‎21、（2013•孝感压轴题）如图1，已知正方形ABCD的边长为1，点E在边BC上，若∠AEF=90°，且EF交正方形外角的平分线CF于点F．‎ ‎（1）图1中若点E是边BC的中点，我们可以构造两个三角形全等来证明AE=EF，请叙述你的一个构造方案，并指出是哪两个三角形全等（不要求证明）；‎ ‎（2）如图2，若点E在线段BC上滑动（不与点B，C重合）．‎ ‎①AE=EF是否总成立？请给出证明；‎ ‎②在如图2的直角坐标系中，当点E滑动到某处时，点F恰好落在抛物线y=﹣x2+x+1上，求此时点F的坐标．‎ ‎（1）解：如图1，取AB的中点G，连接EG． ‎ ‎△AGE与△ECF全等．　 ‎ ‎（2）①若点E在线段BC上滑动时AE=EF总成立．‎ 证明：如图2，在AB上截取AM=EC．‎ ‎∵AB=BC，∴BM=BE，‎ ‎∴△MBE是等腰直角三角形，∴∠AME=180°﹣45°=135°，‎ 又∵CF平分正方形的外角，∴∠ECF=135°，∴∠AME=∠ECF． ‎ 而∠BAE+∠AEB=∠CEF+∠AEB=90°，‎ ‎∴∠BAE=∠CEF，∴△AME≌△ECF．∴AE=EF． ‎ ‎②过点F作FH⊥x轴于H，由①知，FH=BE=CH，‎ 设BH=a，则FH=a﹣1，∴点F的坐标为F（a，a﹣1）‎ ‎∵点F恰好落在抛物线y=﹣x2+x+1上，∴a﹣1=﹣a2+a+1，‎ ‎∴a2=2，（负值不合题意，舍去），∴．‎ ‎∴点F的坐标为．‎ ‎22、（2013•十堰压轴题）已知抛物线y=x2﹣2x+c与x轴交于A．B两点，与y轴交于C点，抛物线的顶点为D点，点A的坐标为（﹣1，0）．‎ ‎（1）求D点的坐标；‎ ‎（2）如图1，连接AC，BD并延长交于点E，求∠E的度数；‎ ‎（3）如图2，已知点P（﹣4，0），点Q在x轴下方的抛物线上，直线PQ交线段AC于点M，当∠PMA=∠E时，求点Q的坐标．‎ 解：（1）把x=﹣1，y=0代入y=x2﹣2x+c得：1+2+c=0∴c=﹣3‎ ‎∴y=x2﹣2x﹣3=y=（x﹣1）2﹣4∴顶点坐标为（1，﹣4）；‎ ‎（2）如图1，连接CD、CB，过点D作DF⊥y轴于点F，‎ 由x2﹣2x﹣3=0得x=﹣1或x=3∴B（3，0）‎ 当x=0时，y=x2﹣2x﹣3=﹣3∴C（0，﹣3）∴OB=OC=3‎ ‎∵∠BOC=90°，∴∠OCB=45°，‎ BC=3‎ 又∵DF=CF=1，∠CFD=90°，∴∠FCD=45°，CD=，‎ ‎∴∠BCD=180°﹣∠OCB﹣∠FCD=90°．∴∠BCD=∠COA 又∵∴△DCB∽△AOC，∴∠CBD=∠OCA 又∵∠ACB=∠CBD+∠E=∠OCA+∠OCB∴∠E=∠OCB=45°，‎ ‎（3）如图2，设直线PQ交y轴于N点，交BD于H点，作DG⊥x轴于G点 ‎∵∠PMA=45°，∴∠EMH=45°，∴∠MHE=90°，∴∠PHB=90°，‎ ‎∴∠DBG+∠OPN=90°‎ 又∴∠ONP+∠OPN=90°，∴∠DBG=∠ONP 又∵∠DGB=∠PON=90°，∴△DGB=∠PON=90°，∴△DGB∽△PON ‎∴即：=‎ ‎∴ON=2，∴N（0，﹣2）‎ 设直线PQ的解析式为y=kx+b则 解得：‎ ‎∴y=﹣x﹣2设Q（m，n）且n＜0，∴n=﹣m﹣2‎ 又∵Q（m，n）在y=x2﹣2x﹣3上，‎ ‎∴n=m2﹣2m﹣3‎ ‎∴﹣m﹣2=m2﹣2m﹣3解得：m=2或m=﹣∴n=﹣3或n=﹣‎ ‎∴点Q的坐标为（2，﹣3）或（﹣，﹣）．‎ ‎23、（2013•恩施州压轴题）如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C和D（3，0）．‎ ‎（1）求直线BD和抛物线的解析式．‎ ‎（2）若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标．‎ ‎（3）在抛物线上是否存在点P，使S△PBD=6？若存在，求出点P的坐标；若不存在，说明理由．‎ 解：（1）∵直线l：y=3x+3与x轴交于点A，与y轴交于点B，∴A（﹣1，0），B（0，3）；‎ ‎∵把△AOB沿y轴翻折，点A落到点C，∴C（1，0）．‎ 设直线BD的解析式为：y=kx+b，‎ ‎∵点B（0，3），D（3，0）在直线BD上，∴，‎ 解得k=﹣1，b=3，∴直线BD的解析式为：y=﹣x+3．‎ 设抛物线的解析式为：y=a（x﹣1）（x﹣3），‎ ‎∵点B（0，3）在抛物线上，∴3=a×（﹣1）×（﹣3），‎ 解得：a=1，‎ ‎∴抛物线的解析式为：y=（x﹣1）（x﹣3）=x2﹣4x+3．‎ ‎（2）抛物线的解析式为：y=x2﹣4x+3=（x﹣2）2﹣1，‎ ‎∴抛物线的对称轴为直线x=2，顶点坐标为（2，﹣1）．‎ 直线BD：y=﹣x+3与抛物线的对称轴交于点M，令x=2，得y=1，∴M（2，1）．‎ 设对称轴与x轴交点为点F，则CF=FD=MN=1，‎ ‎∴△MCD为等腰直角三角形．‎ ‎∵以点N、B、D为顶点的三角形与△MCD相似，∴△BND为等腰直角三角形．‎ 如答图1所示：‎ ‎（I）若BD为斜边，则易知此时直角顶点为原点O，∴N1（0，0）；‎ ‎（II）若BD为直角边，B为直角顶点，则点N在x轴负半轴上，‎ ‎∵OB=OD=ON2=3，∴N2（﹣3，0）；‎ ‎（III）若BD为直角边，D为直角顶点，则点N在y轴负半轴上，‎ ‎∵OB=OD=ON3=3，∴N3（0，﹣3）．‎ ‎∴满足条件的点N坐标为：（0，0），（﹣3，0）或（0，﹣3）．‎ ‎（3）假设存在点P，使S△PBD=6，设点P坐标为（m，n）．‎ ‎（I）当点P位于直线BD上方时，如答图2所示：‎ 过点P作PE⊥x轴于点E，则PE=n，DE=m﹣3．‎ S△PBD=S梯形PEOB﹣S△BOD﹣S△PDE=（3+n）•m﹣×3×3﹣（m﹣3）•n=6，‎ 化简得：m+n=7 ①，‎ ‎∵P（m，n）在抛物线上，∴n=m2﹣4m+3，‎ 代入①式整理得：m2﹣3m﹣4=0，‎ 解得：m1=4，m2=﹣1，∴n1=3，n2=8，∴P1（4，3），P2（﹣1，8）；‎ ‎（II）当点P位于直线BD下方时，如答图3所示：‎ 过点P作PE⊥y轴于点E，则PE=m，OE=﹣n，BE=3﹣n．‎ S△PBD=S梯形PEOD+S△BOD﹣S△PBE=（3+m）•（﹣n）+×3×3﹣（3﹣n）•m=6，‎ 化简得：m+n=﹣1 ②，‎ ‎∵P（m，n）在抛物线上，∴n=m2﹣4m+3，‎ 代入②式整理得：m2﹣3m+4=0，△=﹣7＜0，此方程无解．‎ 故此时点P不存在．‎ 综上所述，在抛物线上存在点P，使S△PBD=6，点P的坐标为（4，3）或（﹣1，8）．‎ ‎24、（2013•鄂州压轴题）在平面直角坐标系中，已知M1（3，2），N1（5，﹣1），线段M1N1平移至线段MN处（注：M1与M，N1与N分别为对应点）．‎ ‎（1）若M（﹣2，5），请直接写出N点坐标．新-课 -标- 第-一- 网 ‎（2）在（1）问的条件下，点N在抛物线上，求该抛物线对应的函数解析式．‎ ‎（3）在（2）问条件下，若抛物线顶点为B，与y轴交于点A，点E为线段AB中点，点C（0，m）是y轴负半轴上一动点，线段EC与线段BO相交于F，且OC：OF=2：，求m的值．‎ ‎（4）在（3）问条件下，动点P从B点出发，沿x轴正方向匀速运动，点P运动到什么位置时（即BP长为多少），将△ABP沿边PE折叠，△APE与△PBE重叠部分的面积恰好为此时的△ABP面积的，求此时BP的长度．‎ 解：（1）由于图形平移过程中，对应点的平移规律相同，‎ 由点M到点M′可知，点的横坐标减5，纵坐标加3，‎ 故点N′的坐标为（5﹣5，﹣1+3），即（0，2）．‎ N（0，2）；‎ ‎（2）∵N（0，2）在抛物线y=x2+x+k上∴k=2‎ ‎∴抛物线的解析式为y=x2+x+2 ‎ ‎（3）∵y=x2+x+2=（x+2）2‎ ‎∴B（﹣2，0）、A（0，2）、E（﹣，1）∵CO：OF=2：‎ ‎∴CO=﹣m，FO=﹣m，BF=2+m ‎∵S△BEC=S△EBF+S△BFC=‎ ‎∴（2+m）（﹣m+1）=‎ 整理得：m2+m=0∴m=﹣1或0 ‎ ‎∵m＜0∴m=﹣1 ‎ ‎（4）在Rt△ABO中，tan∠ABO===‎ ‎∴∠ABO=30°，AB=2AO=4‎ ‎①当∠BPE＞∠APE时，连接A1B则对折后如图2，A1为对折后A的所落点，△EHP是重叠部分．‎ ‎∵E为AB中点，∴S△AEP=S△BEP=S△ABP ‎∵S△EHP=S△ABP ‎∴=S△EHP=S△BHP=S△ABP∴A1H=HP，EH=HB=1‎ ‎∴四边形A1BPE为平行四边形∴BP=A1E=AE=2即BP=2 ‎ ‎②当∠BPE=∠APE时，重叠部分面积为△ABP面积的一半，不符合题意；‎ ‎③当∠BPE＜∠APE时．‎ 则对折后如图3，A1为对折后A的所落点．△EHP是重叠部分 ‎∵E为AB中点，∴S△AEP=S△BEP=S△ABP ‎∵S△EHP=S△ABP∴S△EBH=S△EHP==S△ABP∴BH=HP，EH=HA1=1‎ 又∵BE=EA=2∴EHAP，∴AP=2‎ 在△APB中，∠ABP=30°，AB=4，AP=2∴∠APB=90°，∴BP=，‎ 综合①②③知：BP=2或；‎ ‎25、（2013•黔西南州压轴题）如图，已知抛物线经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C ‎（1）求抛物线的函数解析式．‎ ‎（2）设点D在抛物线上，点E在抛物线的对称轴上，且以AO为边的四边形AODE是平行四边形，求点D的坐标．‎ ‎（3）P是抛物线上第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P，M，A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．‎ 解：（1）设抛物线的解析式为y=ax2+bx+c（a≠0），‎ 将点A（﹣2，0），B（﹣3，3），O（0，0），代入可得：，‎ 解得：．‎ 故函数解析式为：y=x2+2x．‎ ‎（2）当AO为平行四边形的边时，DE∥AO，DE=AO，由A（﹣2，0）知：DE=AO=2，‎ 若D在对称轴直线x=﹣1左侧，‎ 则D横坐标为﹣3，代入抛物线解析式得D1（﹣3，3），‎ 若D在对称轴直线x=﹣1右侧，‎ 则D横坐标为1，代入抛物线解析式得D2（1，3）．‎ 综上可得点D的坐标为：（﹣3，3）或（1，3）．‎ ‎（3）存在．如图：∵B（﹣3，3），C（﹣1，﹣1），‎ 根据勾股定理得：BO2=18，CO2=2，BC2=20，‎ ‎∵BO2+CO2=BC2，∴△BOC是直角三角形，‎ 假设存在点P，使以P，M，A为顶点的 三角形与△BOC相似，‎ 设P（x，y），由题意知x＞0，y＞0，且y=x2+2x，‎ ‎①若△AMP∽△BOC，则=，‎ 即x+2=3（x2+2x），得：x1=，x2=﹣2（舍去）．‎ 当x=时，y=，即P（，），‎ ‎②若△PMA∽△BOC，则=，‎ 即：x2+2x=3（x+2），得：x1=3，x2=﹣2（舍去）‎ 当x=3时，y=15，即P（3，15）．‎ 故符合条件的点P有两个，分别是P（，）或（3，15）．‎