中考数学综合型问题目押轴题目专练2 3页

‎5.某花圃用花盆培育某种花苗，经过实验发现每盆的盈利与每盆的株数构成一定的关系，每盆植入3株时，平均单株盈利3元；以同样的栽培条件，若每盆增加1株，平均单株盈利就减少0.5元，要使每盆的盈利达到10元，每盆应植多少株？‎ 小明的解法如下：‎ 解：设每盆花苗增加x株，则每盆花苗有（x+3）株，平均单株盈利为（3-0.5x）元，由题意得：(x+3)(3-0.5x)=10.‎ 化简，整理得：x2-3x+2=0.‎ 解：这个方程，得x1=1,x2=2‎ 答：要使每盆的盈利达到10元，每盆应植入4株或5株.‎ （1） 本题涉及的主要数量有每盆花苗的株数，平均单株盈利，每盆花苗的盈利等，请写出两个不同的等量关系:__________________________________________________.‎ ‎（2）请用一种与小明不相同的方法求解上述问题.‎ ‎【解题思路】（1）本题应该认真审题，本题中包含有每盆的盈利相当于单株盈利×每盆里所载花苗的株数.要盈利10元就必须增加花苗的株数，这时单株的盈利会相应的减少，这时所需要注意的.另外还有一个等量关系，就是盆里所载的花苗株数相当于原有的花苗株数+增加的花苗株数.(2)本题可以利用函数，画图像等方法去解决.‎ ‎【答案】（1）平均单株盈利×株数=每盆盈利.‎ ‎ 平均单株盈利=3-0.5×每盆增加的株数.‎ ‎ 每盆的株数=3+每盆增加的株数.‎ ‎ (2)解法1.（列表法）‎ 每盆植入的株数 平均单株盈利（元）‎ 每盆盈利（元）‎ ‎3‎ ‎3‎ ‎9‎ ‎4‎ ‎2.5‎ ‎10‎ ‎5‎ ‎2‎ ‎10‎ ‎6‎ ‎1.5‎ ‎9‎ ‎7‎ ‎1‎ ‎7‎ ‎…‎ ‎…‎ ‎…‎ 答：每盆盈利要达到10元，每盆应该植入4株或5株.‎ 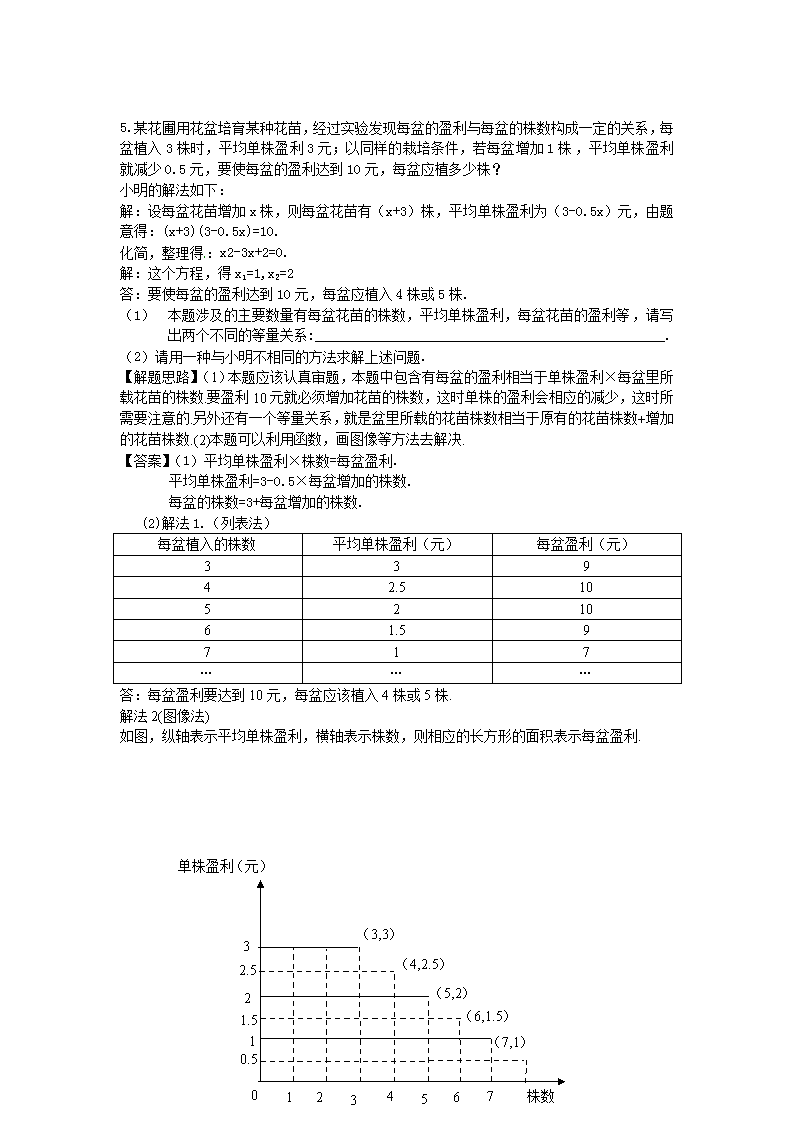解法2(图像法)‎ 如图，纵轴表示平均单株盈利，横轴表示株数，则相应的长方形的面积表示每盆盈利.‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ 单株盈利（元）‎ 株数 ‎（3,3）‎ ‎（4,2.5）‎ ‎（5,2）‎ ‎（6,1.5）‎ ‎（7,1）‎ ‎0.5‎ ‎1‎ ‎1.5‎ ‎2‎ ‎2.5‎ ‎3‎ 答：每盆盈利要达到10元，每盆应该植入4株或5株.‎ 解法3.（函数法）‎ 解：设每盆花增加x株时，每盆的盈利为y元，根据题意，得 y=(x+3)（3-0.5x）‎ 当y=10时，（x+3）(3-0.5x)=10‎ 解这个方程得，x1=1,x2=2‎ 答：每盆盈利要达到10元，每盆应该植入4株或5株.‎ 解法4：（列分式方程）‎ 解：设每盆花苗增加x株时，每盆的盈利10元，根据题意，得 解这个方程得，x1=1,x2=2‎ 经检验，x1=1,x2=2是所列方程得解.‎ 答：每盆盈利要达到10元，每盆应该植入4株或5株.‎ ‎【点评】本题考查的是应用多种方法去解决实际应用题，他一改往常的只用方程解决应用题，这就要求学生在知识上不是单一的，此题多元化得去考查学生对所学知识的掌握，可谓是一道好题.难度中等.‎ ‎6 ．如图1，过△ABC顶点A分别对边BC上的高AD和中线AE，点D是垂足，点E是BC中点，规定，特别地，当点D、E重合时，规定。另外，对作类似的规定。‎ ‎（1）如图2，已知在Rt△ABC中，∠A=30°，求；‎ ‎（2）在每一个小正方形边均为1的4×4方格纸上，画一个△ABC使其顶点在格点（格点即每个小正方形的顶点）上，且，面积也为2；‎ ‎（3）判断下列三个命题的真假。（真命题∨，假命题×）‎ ‎①若△ABC中，则△ABC为锐角三角形；（ ▲ ）‎ ‎②若△ABC中，则△ABC为直角三角形；（ ▲ ）‎ ‎③若△ABC中，则△ABC为钝角三角形；（ ▲ ）‎ ‎【解题思路】本题是新定义的题目，理解题目的意思是解这题的关键 （1） 求只要做出中线AE,再由定义即可得；求只要分别做出高线CD和中线CE，再由直角三角形斜边上的中线等于斜边上的一半，转化到直角三角形CDE来，用余弦函数就求 （2） 由知=2，又E是BC的中点，可以画出一个如下图的图形 ‎（3）判断①当∠A为钝角时存在，故错误，判断②，③可以由（1），（2）做出判断 ‎【答案】解:如图作BC边上的中线,又AC⊥BC,∴…‎ 过点C分别作AB边上的高CE和中线CF作BC边上的中线 ‎ ‎∵∠ACB=90°‎ ‎∴AF=CF ∴∠ACF=∠CAF=30°‎ ‎∴∠CFE=60° ∴‎ ‎（2）‎ ‎（3）×,∨,∨‎ ‎【点评】是一道好题，设计新颖，可以考查学生的阅读能力，画图能力，以及知识的迁移能力。难度适中。‎