2013中考数学模拟试题及答案五 11页

‎2013中考数学模拟试题及答案五 一、选择题（本大题共10题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请将正确选项的字母写在答卷相应的位置上．‎ ‎1．下列各式：①；②；③；④，计算结果为负数的个数有 A．4个 B．3个 C．2个 D．1个 ‎2．下列计算正确的是 A． B． C． D．‎ ‎3．截至2012年五月底，我国股市开户总数约95000000，95000000用科学计数法表示为学科王 A. 9.5‎×106 B. 9.5×‎107 C. 9.5×108 D. 9.5×109学科王4．如图，图1表示正六棱柱形状的高式建筑物，图2中的正六边形部分是从该建筑物的正上方看到的俯视图，P、Q、M、N表示小明在地面上的活动区域．小明想同时看到该建筑物的三个侧面，他应在 ‎ ‎ A．P区域 B．Q区域 C．M区域 D．N区域 ‎ ‎5．将直径为‎60cm的圆形铁皮，做成三个相同的圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），那么每个圆锥容器的底面半径为 A．‎10cm B．‎20cm C．‎30cm D．‎‎60cm ‎6．某学校用420元钱到商场去购买“‎84”‎消毒液，经过还价，每瓶便宜0.5元，结果比用原价多买了20瓶，求原价每瓶多少元？若设原价每瓶元，则可列出方程为 ‎ A． B．‎ C． D．‎ D C B E A H ‎7．在直角梯形中，，为边上一点，，且．连接交对角线于，连接．下列结论：①；②为等边三角形；③；④ ．其中结论正确的是 A．①② B．①②④ C．③④ D．①②③④‎ ‎8．如图，是的直径，弦，是弦的中点， ．若动点以的速度从点出发沿着方向运动，设运动时间为，连结，当是直角三角形时，（s）的值为 A． B．‎1 C．或1 D．或1 或 ‎ ‎9．如图，无盖无底的正方体纸盒，，分别为棱，上的点，且，若将这个正方体纸盒沿折线裁剪并展开，得到的图形是 A B C·‎ D E y x A．一个六边形 B．一个平行四边形 C．两个直角三角形 D．一个直角三角形和一个直角梯形 ‎10．如图，已知A、B两点的坐标分别为(－2，0)、(0，1)，⊙C 的圆心坐标为(0，－1)，半径为1．若D是⊙C上的一个动点，射线AD与y轴交于点E，则△ABE面积的最大值是 A．3 B． C． D．4‎ 二、填空题（本大题共6小题，每小题4分，共24分）请将下列各题的正确答案填写在答卷相应的位置上 ‎11. 分解因式: = ．‎ ‎12．函数的自变量x的取值范围是_____ ．‎ ‎13．如图，在等腰梯形ABCD中，AD∥BC，对角线AC⊥BD于 点O，AE⊥BC，DF⊥BC，垂足分别为E、F，AD＝4，BC＝8，则AE＋EF＝ ．‎ ‎14．如图，直线经过，两点，则不等式的解集为 ．‎ ‎15．已知⊙与⊙两圆内含，，⊙的半径为5，那 么⊙的半径的取值范围是 ．‎ ‎16．如图，直线y=－x+2与x 轴交于C，与y轴交于D， 以CD 为边作矩形CDAB，点A在x轴上，双曲线y=(k<0)经过点B与直线CD交于E，EM⊥x轴于M，则S四边形BEMC= ．‎ 三、解答题（一）（本大题共3小题，每小题5分，共15分）‎ ‎17．计算 +‎ ‎18．先化简： ，并从0，，2中选一个合适的数作为的值代入求值 ‎19． 如图，四边形ABCD中，AB=AC=AD，BC=CD，锐角∠BAC 的角平分线AE交BC于点E，AF是CD边上的中线，且PC⊥CD与AE交于点P，QC⊥BC与AF交于点Q．求证：四边形APCQ是菱形．‎ 四、解答题（二）（本大题共3小题，每小题8分，共24分）‎ 非常赞成 ‎26%‎ 不 赞成 无所谓 基本赞成 ‎50%‎ 不赞成 无所谓 ‎16‎ 非常 ‎ 赞成 人数 ‎200‎ ‎160‎ ‎120‎ ‎80‎ ‎40‎ ‎0‎ ‎0‎ 基本 ‎ 赞成 ‎200‎ 图①‎ 选项 图②‎ ‎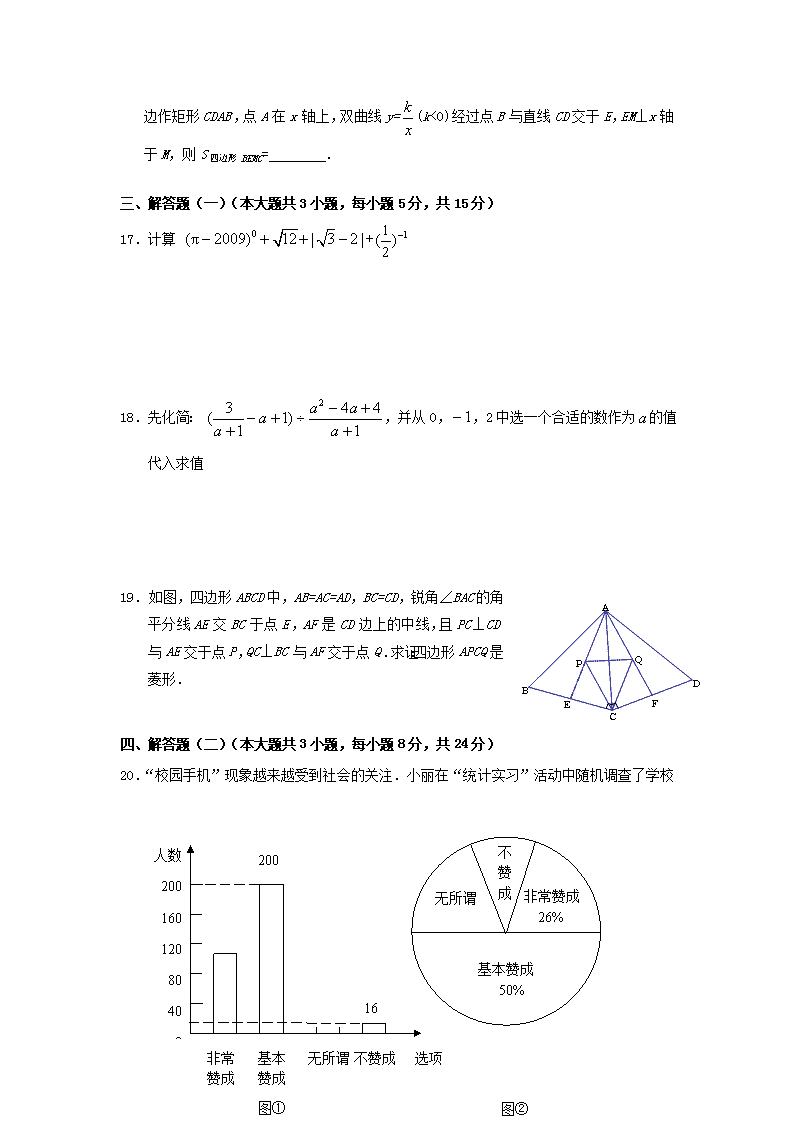20．“校园手机”现象越来越受到社会的关注．小丽在“统计实习”‎ 活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法，统计整理并制作了如下的统计图：‎ ‎（1）求这次调查的家长总数及家长表示“无所谓”的人数，并补全图①；‎ ‎（2）求图②中表示家长“无所谓”的圆心角的度数；‎ ‎（3）从这次接受调查的家长中，随机抽查一个，恰好是“不赞成”态度的家长的概率是多少？‎ ‎21．如图，台风中心位于点P，并沿东北方向PQ移动，已知台风移动的速度为30千米/时，受影响区域的半径为‎200千米，B市位于点P的北偏东75°方向上，距离点P ‎320千米处. ‎ ‎（1）说明本次台风会影响B市；‎ ‎（2）求这次台风影响B市的时间．‎ ‎22． A、B两城间的公路长为450千米，甲、乙两车同时从A城出发沿这一公路驶向B城，甲车到达B城1小时后沿原路返回．如图是它们离A城的路程y（千米）与行驶时间 ‎ x（小时）‎ y（千米）‎ ‎450‎ ‎10‎ ‎4 5‎ O F C E D x（小时）之间的函数图像．‎ ‎（1）求甲车返回过程中y与x之间的函数解析式， 并写出x的取值范围；‎ ‎（2）乙车行驶6小时与返回的甲车相遇，求乙车 的行驶速度．‎ 五、解答题（三）（本大题共3小题，每小题9分，共27分）‎ B A F E D C M ‎23．在圆内接四边形ABCD中，CD为∠BCA外角的平分线，F为上一点，BC＝AF，延长DF与BA的延长线交于E ‎．‎ ‎（1）求证△ABD为等腰三角形．‎ ‎（2）求证AC•AF＝DF•FE．‎ ‎24．我省某镇的一种特产由于运输原因，长期只能在当地销售．当地政府对该特产的销售投资收益为：每投入x万元，可获得利润P＝－(x－60)2＋41（万元）．当地政府拟在“十二•五”规划中加快开发该特产的销售，其规划方案为：在规划前后对该项目每年最多可投入100万元的销售投资，在实施规划5年的前两年中，每年都从100万元中拨出50万元用于修建一条公路，两年修成，通车前该特产只能在当地销售；公路通车后的3年中，该特产既在本地销售，也在外地销售．在外地销售的投资收 益为：每投入x万元，可获利润Q＝－(100－x)2＋(100－x)＋160（万元）．‎ ‎（1）若不进行开发，求5年所获利润的最大值是多少？‎ ‎（2）若按规划实施，求5年所获利润（扣除修路后）的最大值是多少？‎ ‎（3）根据（1）、（2），该方案是否具有实施价值？‎ ‎25．如图所示，过点F（0，1）的直线y＝kx＋b与抛物线y＝ x2交于M（x1，y1）和N（x2，y2）两点（其中x1＜0，x2＜0）．‎ F M N N1‎ M1‎ F1‎ O y x l ‎ ‎ ‎（1）求b的值．‎ ‎（2）求x1•x2的值 ‎（3）分别过M、N作直线l：y＝－1的垂线，垂足分别是M1、N1，判断△M1FN1的形状，并证明你的结论．‎ ‎（4）对于过点F的任意直线MN，是否存在一条定直线m，使m与以MN为直径的圆相切．如果有，请求出这条直线m的解析式；如果没有，请说明理由．‎ 参考答案 ‎ 一、选择题（本大题共10题，每小题3分，共30分）‎ 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答 案 B B B B A B B D B B 二、填空题（本大题共6小题，每小题4分，共24分）‎ ‎11．m(x－3)2 12. x≤2 13. 10 ‎ ‎14. 15. 16. ‎ 三、解答题（一）（本大题共3小题，每小题5分，共15分）‎ ‎17．解：原式=1+2+2﹣+2 …………3分 ‎=5+． …………2分 ‎18．解：原式=×， …………1分 ‎=﹣× ………1分 ‎=﹣， …………1分 当a=0时，原式=1． …………2分 ‎19．证明：∵AC=AD，AF是CD边上的中线，‎ ‎∴∠AFC=90°，‎ ‎∴∠ACF+∠CAF=90°， …………1分 ‎∵∠ACF+∠PCA=90°，‎ ‎∴∠PCA=∠CAF，‎ ‎∴PC∥AQ，‎ 同理：AP∥QC， ‎ ‎∴四边形APCQ是平行四边形． …………1分 ‎∵AF∥CP，AE∥CQ，‎ ‎∴∠EPC=∠PAF=∠FQC，‎ ‎∵AB=AC，AE平分∠BAC，‎ ‎∴CE=BE=CB， …………1分 ‎∵AF是CD边上的中线，‎ ‎∴CF=CD，‎ ‎∵CB=DC，‎ ‎∴CE=CF， …………1分 ‎∵PC⊥CD，QC⊥BC，‎ ‎∴∠ECP+∠PCQ=∠QCF+∠PCQ=90°，‎ ‎∴∠PCE=∠QCF，‎ ‎∴△PEC≌△QFC（AAS），‎ ‎∴PC=QC，‎ ‎∴四边形APCQ是菱形． …………1分 四、解答题（二）（本大题共3小题，每小题8分，共24分）‎ ‎20．解：（1）这次调查的家长总数为：200÷50%=400名， …………1分 家长表示“无所谓”的人数为：400﹣200﹣16﹣400×26%=80名，‎ ‎…………1分 如图，补全图①； ‎ ‎…………2分 ‎（2）图②中表示家长“无所谓”的圆心角的度数为80÷400×360=72°； …………2分 ‎（3）P（恰好是“不赞成”态度的家长）16÷400=．； …………2分 ‎21．解：（1）如图，作BH⊥PQ于点H, …………1分 在Rt△BHP中，已知 PB = 320, ÐBPQ = 30°, …………1分 ‎∴BH = 320sin30° = 160 < 200, …………1分 ‎∴本次台风会影响B市. …………1分 ‎（2）如图所示, 若台风中心移动到P1时, 台风开始影响B市, 台风中心移动到P2时, 台风影响结束． …………1分 由（1）得BH = 160, 又 BP1=BP2 = 200, …………1分 ‎∴P1P2 = 2=240, …………1分 ‎∴台风影响的时间t = = 8(小时). ………1分 ‎22．解：（1）设甲车返回过程中y与x之间的函数解析式， …………‎ ‎1分 ‎∵图像过（5，450），（10，0）两点， …………1分 ‎∴ …………1分 解得 …………1分 ‎∴．函数的定义域为5≤≤10. …………2分 ‎（2）当时，， …………1分 ‎ （千米/小时）． …………1分 五、解答题（三）（本大题共3小题，每小题9分，共27分）‎ ‎23．解：（1）证法一：连CF、BF ‎∠ACD=∠MCD=∠CDB＋∠CBD=∠CFB＋∠CFD=∠DFB 而∠ACD=∠DFB=∠DAB 又∠ACD=∠DBA ‎∴∠DAB=∠DBA ‎ ‎∴△ABD为等腰三角形 ……（3分）‎ 证法二：由题意有∠MCD=∠ACD =∠DBA,‎ 又∠MCD+∠BCD=∠DAB+∠BCD=180°,‎ ‎∴∠MCD=∠DAB，‎ ‎∴∠DAB=∠DBA，即△ABD为等腰三角形 ……（3分）‎ ‎（2）由（1）知AD=BD，BC=AF，则弧AFD=弧BCD，弧AF=弧BC，‎ ‎∴弧CD=弧DF,∴弧CD=弧DF……① ……（4分）‎ 又BC=AF,‎ ‎∴∠BDC=∠ADF,∠BDC＋∠BDA=∠ADF＋∠BDA，‎ 即∠CDA=∠BDF，‎ 而∠FAE＋∠BAF=∠BDF＋∠BAF=180°，∴∠FAE=∠BDF=∠CDA，‎ 同理∠DCA=∠AFE ……（6分）‎ ‎∴在△CDA与△FDE中，∠CDA=∠FAE，∠DCA=∠AFE ‎∴△CDA∽△FAE ‎∴CD·EF=AC·AF，‎ 又由①有AC·AF=DF·EF 命题即证 ……（9分）‎ ‎24．解：（1）由P=－（x－60）2＋41知，每年只需从100万元中拿出60万元投资，即可获得最大利润41万元，‎ 则不进行开发的5年的最大利润P1=41×5=205（万元） ……（2分）‎ ‎（2）若实施规划，在前2年中，当x=50时，‎ 每年最大利润为：P=－（50－60）2+41=40万元，‎ 前2年的利润为：40×2=80万元，扣除修路后的纯利润为：80－50×2=－20万元. ……（4分）‎ 设在公路通车后的3年中，每年用x万元投资本地销售，而用剩下的（100-x）万元投资外地销售，则其总利润W=［- （x-60）2＋41＋（- x2＋ x＋160］×3=-3（x-30）2＋3195‎ 当x=30时，W的最大值为3195万元，‎ ‎∴5年的最大利润为3195-20=3175（万元） ……（7分）‎ ‎（3）规划后5年总利润为3175万元，不实施规划方案仅为205万元，故具有很大的实施价值. ……（9分）‎ ‎25．解：（1）把点F（0，1）坐标代入y=kx＋b中得b=1. ……（1分）‎ ‎（2）由y= x2和y=kx＋1得 x2-kx-1=0‎ 化简得 x1=2k-2，x2=2k＋2x1·x2=-4……（3分）学科王 ‎（3）△M1FN1是直角三角形（F点是直角顶点）.理由如下：‎ 设直线l与y轴的交点是F1‎ FM12=FF12+M‎1F12=x12＋4 FN12=FF12＋F1N12=x22＋4‎ M1N12=（x1-x2）2=x12+x22-2x1x2=x12+x22+8‎ ‎∴FM12+FN12=M1N12‎ ‎∴△M1FN1是以F点为直角顶点的直角三角形. ……（6分）‎ ‎（4）符合条件的定直线m即为直线l：y=-1.‎ 过M作MH⊥NN1于H，‎ MN2=MH2+NH2 =（x1-x2）2+（y1-y2）2‎ ‎=（x1-x2）2+［（kx1+1）-(kx2+1)］2‎ ‎=（x1-x2）2+k2（x1-x2）2‎ ‎= (k2+1)（x1-x2）2‎ ‎=(k2+1)(4 ）2‎ ‎=16（k2+1)2 ‎ ‎∴MN=4(k2+1)‎ 分别取MN和M1N1的中点P，P1， ‎ PP1= （MM1+NN1）= (y1+1+y2+1)= （y1+y2）+1= k(x1+x1)+2=2k2+2=2(k2+1) ∴PP1= MN 即线段MN的中点到直线l的距离等于MN长度的一半.‎ ‎∴以MN为直径的圆与l相切. ……（9分）‎