中考数学专题复习与圆有关的动点问题精品含答案 18页

‎2014年中考数学专题复习：与圆有关的动点问题 ‎1、如图，⊙O的直径AB=4，C为圆周上一点，AC=2，过点C作⊙O的切线DC，P点为优弧CBA上一动点（不与A．C重合）．‎ ‎（1）求∠APC与∠ACD的度数；‎ ‎（2）当点P移动到CB弧的中点时，求证：四边形OBPC是菱形．‎ ‎（3）P点移动到什么位置时，△APC与△ABC全等，请说明理由．‎ ‎2、如图，在⊙O上位于直径AB的异侧有定点C和动点P，AC=AB，点P在半圆弧AB上运动（不与A、B两点重合），过点C作直线PB的垂线CD交PB于D点．‎ ‎（1）如图1，求证：△PCD∽△ABC；‎ ‎（2）当点P运动到什么位置时，△PCD≌△ABC？请在图2中画出△PCD并说明理由；‎ ‎（3）如图3，当点P运动到CP⊥AB时，求∠BCD的度数．‎ ‎3、如图，在半径为2的扇形AOB中，∠AOB=90°，点C是弧AB上的一个动点（不与点A、B重合）OD⊥BC，OE⊥AC，垂足分别为D、E．‎ ‎（1）当BC=1时，求线段OD的长；‎ ‎（2）在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度，如果不存在，请说明理由；‎ ‎（3）设BD=x，△DOE的面积为y，求y关于x的函数关系式，并写出它的定义域．‎ ‎4、如图，菱形ABCD的边长为‎2cm，∠DAB=60°．点P从A点出发，以cm/s的速度，沿AC向C作匀速运动；与此同时，点Q也从A点出发，以‎1cm/s的速度，沿射线AB作匀速运动．当P运动到C点时，P、Q都停止运动．设点P运动的时间为ts．‎ ‎（1）当P异于A．C时，请说明PQ∥BC；‎ ‎（2）以P为圆心、PQ长为半径作圆，请问：在整个运动过程中，t为怎样的值时，⊙P与边BC分别有1个公共点和2个公共点？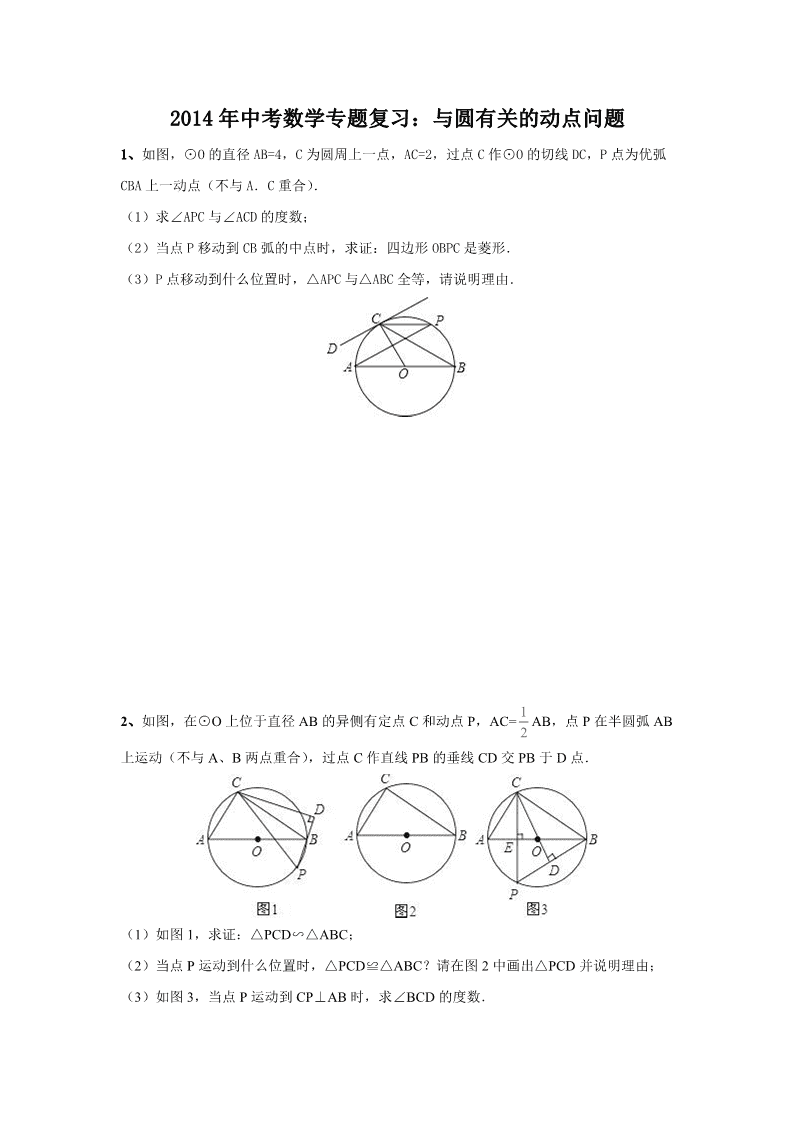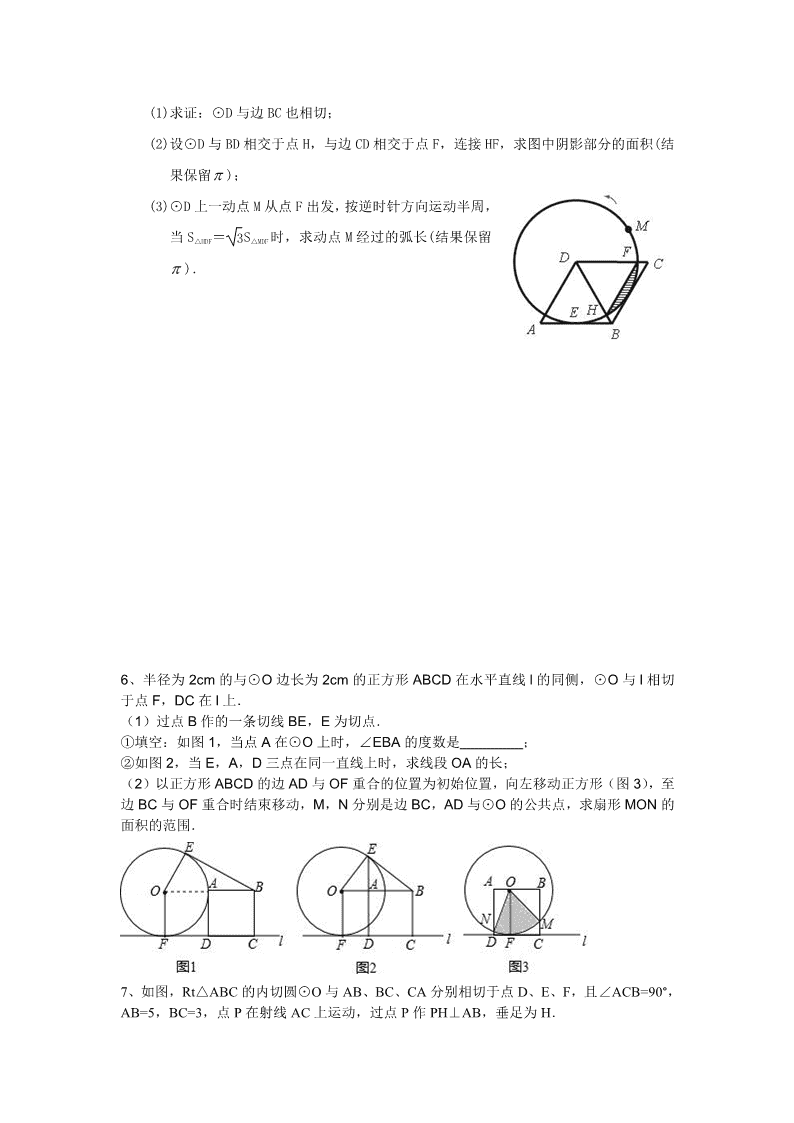‎ ‎5、如图，在菱形ABCD中，AB＝2，∠A＝60º，以点D为圆心的⊙D与边AB相切于点E．‎ ‎(1)求证：⊙D与边BC也相切；‎ ‎(2)设⊙D与BD相交于点H，与边CD相交于点F，连接HF，求图中阴影部分的面积(结果保留)；‎ ‎(3)⊙D上一动点M从点F出发，按逆时针方向运动半周，当S△HDF＝S△MDF时，求动点M经过的弧长(结果保留)．‎ ‎6、半径为‎2cm的与⊙O边长为‎2cm的正方形ABCD在水平直线l的同侧，⊙O与l相切于点F，DC在l上． （1）过点B作的一条切线BE，E为切点． ①填空：如图1，当点A在⊙O上时，∠EBA的度数是 30°‎ ‎； ②如图2，当E，A，D三点在同一直线上时，求线段OA的长； （2）以正方形ABCD的边AD与OF重合的位置为初始位置，向左移动正方形（图3），至边BC与OF重合时结束移动，M，N分别是边BC，AD与⊙O的公共点，求扇形MON的面积的范围． ‎ ‎7、如图，Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F，且∠ACB=90°，AB=5，BC=3，点P在射线AC上运动，过点P作PH⊥AB，垂足为H．‎ ‎（1）直接写出线段AC、AD及⊙O半径的长；‎ ‎（2）设PH=x，PC=y，求y关于x的函数关系式；‎ ‎（3）当PH与⊙O相切时，求相应的y值．‎ ‎8、如图1，正方形ABCD的边长为2，点M是BC的中点，P是线段MC上的一个动点（不与M、C重合），以AB为直径作⊙O，过点P作⊙O的切线，交AD于点F，切点为E．‎ ‎（1）求证：OF∥BE；‎ ‎（2）设BP=x，AF=y，求y关于x的函数解析式，并写出自变量x的取值范围；‎ ‎（3）延长DC、FP交于点G，连接OE并延长交直线DC与H（图2），问是否存在点P，使△EFO∽△EHG（E、F、O与E、H、G为对应点）？如果存在，试求（2）中x和y的值；如果不存在，请说明理由．‎ ‎9、如图，⊙O的半径为1，直线CD经过圆心O，交⊙O于C、D两点，直径AB⊥CD，点M是直线CD上异于点C、O、D的一个动点，AM所在的直线交于⊙O于点N，点P是直线CD上另一点，且PM=PN．‎ ‎（1）当点M在⊙O内部，如图一，试判断PN与⊙O的关系，并写出证明过程；‎ ‎（2）当点M在⊙O外部，如图二，其它条件不变时，（1）的结论是否还成立？请说明理由；‎ ‎（3）当点M在⊙O外部，如图三，∠AMO=15°，求图中阴影部分的面积．‎ ‎10、如图，在⊙O中，直径AB⊥CD，垂足为E，点M为OC上动点，AM的延长线交⊙O于点G，交过C的直线于F，∠1=∠2，连结CB与DG交于点N．‎ ‎（1）求证：CF是⊙O的切线；‎ ‎（2）点M在OC上移动时（点M不与O、C点重合），探究△ACM与△DCN之间关系，并证明 ‎（3）若点M移动到CO的中点时，⊙O的半径为4，cos∠BOC=，求BN的长．‎ ‎11、如图，已知AB是圆O的直径，BC是圆O的弦，弦ED⊥AB于点F,交BC 于点G，过点C作圆O的切线与ED的延长线交于点P．‎ ‎ (1）求证：PC＝PG；‎ ‎ （2）点C在劣弧AD上运动时，其他条件不变，若点G是BC的中点，试探究CG、BF、BO三者之间的数量关系，并写出证明过程；‎ ‎ （3）在满足（2）的条件下，已知圆为O的半径为5,若点O到BC的距离为时，求弦ED的长．‎ ‎12、如图1，已知⊙O的半径长为3，点A是⊙O上一定点，点P为⊙O上不同于点A的动点．‎ ‎（1）当时，求AP的长；‎ ‎（2）如果⊙Q过点P、O，且点Q在直线AP上（如图2），设AP＝x，QP＝y，求y关于x的函数关系式，并写出函数的定义域；‎ ‎（3）在（2）的条件下，当时（如图3），存在⊙M与⊙O相内切，同时与⊙Q相外切，且OM⊥OQ，试求⊙M的半径的长．‎ 图1 图2 图3 ‎ 答案：‎ ‎1、解：（1）连接AC，如图所示：‎ ‎∵AB=4，∴OA=OB=OC=AB=2。‎ 又∵AC=2，∴AC=OA=OC。∴△ACO为等边三角形。‎ ‎∴∠AOC=∠ACO=∠OAC=60°，‎ ‎∴∠APC=∠AOC=30°。‎ 又DC与圆O相切于点C，∴OC⊥DC。∴∠DCO=90°。‎ ‎∴∠ACD=∠DCO﹣∠ACO=90°﹣60°=30°。‎ ‎ （2）连接PB，OP，‎ ‎∵AB为直径，∠AOC=60°，∴∠COB=120°。‎ 当点P移动到弧CB的中点时，∠COP=∠POB=60°。‎ ‎∴△COP和△BOP都为等边三角形。∴AC=CP=OA=OP。‎ ‎∴四边形AOPC为菱形。‎ ‎（3）当点P与B重合时，△ABC与△APC重合，显然△ABC≌△APC。‎ 当点P继续运动到CP经过圆心时，△ABC≌△CPA，理由为：‎ ‎∵CP与AB都为圆O的直径，∴∠CAP=∠ACB=90°。‎ 在Rt△ABC与Rt△CPA中，AB=CP，AC=AC ‎∴Rt△ABC≌Rt△CPA（HL）。‎ 综上所述，当点P与B重合时和点P运动到CP经过圆心时，△ABC≌△CPA。‎ ‎2、解：（1）证明：∵AB是⊙O的直径，∴∠ACB=90°。‎ ‎∵PD⊥CD，∴∠D=90°。∴∠D=∠ACB。‎ ‎∵∠A与∠P是所对的圆周角，∴∠A=∠P，∴△PCD∽△ABC。‎ ‎（2）当PC是⊙O的直径时，△PCD≌△ABC。理由如下：‎ ‎∵AB，PC是⊙O的半径，∴AB=PC。‎ ‎∵△PCD∽△ABC，∴△PCD≌△ABC。‎ 画图如下：‎ ‎（3）∵∠ACB=90°，AC=AB，∴∠ABC=30°。‎ ‎∵△PCD∽△ABC，∴∠PCD=∠ABC=30°。‎ ‎∵CP⊥AB，AB是⊙O的直径，∴。∴∠ACP=∠ABC=30°。‎ ‎∴∠BCD=∠AC﹣∠ACP﹣∠PCD=90°﹣30°﹣30°=30°。‎ ‎3、解：（1）∵点O是圆心，OD⊥BC，BC=1，∴BD=BC=。‎ ‎ 又∵OB=2，∴。‎ ‎（2）存在，DE是不变的。‎ 如图，连接AB，则。‎ ‎∵D和E是中点，∴DE=。‎ ‎（3）∵BD=x，∴。‎ ‎∵∠1=∠2，∠3=∠4，∠AOB=900。‎ ‎∴∠2+∠3=45°。‎ 过D作DF⊥OE，垂足为点F。∴DF=OF=。‎ 由△BOD∽△EDF，得，即 ‎，解得EF=x。‎ ‎∴OE=。‎ ‎∴。‎ ‎4、解：（1）∵四边形ABCD是菱形，且菱形ABCD的边长为2，‎ ‎∴AB=BC=2，∠BAC=∠DAB。‎ 又∵∠DAB=60°，∴∠BAC=∠BCA=30°。‎ 如图1，连接BD交AC于O。‎ ‎∵四边形ABCD是菱形，‎ ‎∴AC⊥BD，OA=AC。‎ ‎∴OB=AB=1。∴OA=，AC=2OA=2。‎ 运动ts后，AP=t，AO=t，∴。‎ 又∵∠PAQ=∠CAB，∴△PAQ∽△CAB.∴∠APQ=∠ACB.‎ ‎∴PQ∥BC.‎ ‎（2）如图2，⊙P与BC切于点M，连接PM，则PM⊥BC。‎ 在Rt△CPM中，∵∠PCM=30°，∴PM=。‎ 由PM=PQ=AQ=t，即=t，解得t=，‎ 此时⊙P与边BC有一个公共点。‎ 如图3，⊙P过点B，此时PQ=PB，‎ ‎∵∠PQB=∠PAQ+∠APQ=60°‎ ‎∴△PQB为等边三角形。∴QB=PQ=AQ=t。∴t=1。‎ ‎∴当时，⊙P与边BC有2个公共点。‎ 如图4，⊙P过点C，此时PC=PQ，即 =t ‎∴t=。‎ ‎∴当1≤t≤时，⊙P与边BC有一个公共点。‎ 当点P运动到点C，即t=2时，Q、B重合，⊙P过点B，‎ 此时，⊙P与边BC有一个公共点。‎ 综上所述，当t=或1≤t≤或t=2时，⊙P与菱形ABCD的边BC有1个公共点；当时，⊙P与边BC有2个公共点。‎ ‎5、解：（1）证明：连接DE，过点D作DN⊥BC，垂足为点N。‎ ‎ ∵四边形ABCD是菱形，∴BD平分∠ABC。‎ ‎ ∵⊙D与边AB相切于点E，∴DE⊥AB。∴DN=DE。‎ ‎ ∴⊙D与边BC也相切。‎ ‎（2）∵四边形ABCD是菱形，AB＝2，∴AD＝AB＝2。‎ 又∵∠A＝60º，∴DE＝ADsin600＝3，即⊙D的半径是3。‎ 又∵∠HDF＝∠HADC＝60º，DH＝DF，∴△HDF是等边三角形。‎ 过点H作HG⊥DF，垂足为点G，则HG＝3sin600＝。‎ ‎∴。‎ ‎∴。‎ ‎（3）假设点M运动到点M1时，满足S△HDF＝S△MDF，过点M1作M1P⊥DF，垂足为点P，则，解得。‎ ‎ ∴。∴∠M1DF＝30º。‎ 此时动点M经过的弧长为：。‎ 过点M1作M‎1M2‎∥DF交⊙D于点M2，‎ 则满足，‎ 此时∠M2DF＝150º，动点M经过的弧长为：。‎ ‎6、7．解：（1）①∵半径为‎2cm的与⊙O边长为‎2cm的正方形ABCD在水平直线l的同侧，当点A在⊙O上时，过点B作的一条切线BE，E为切点， ∴OB=4，EO=2，∠OEB=90°， ∴∠EBA的度数是：30°； ②如图2， ∵直线l与⊙O相切于点F， ∴∠OFD=90°， ∵正方形ADCB中，∠ADC=90°， ∴OF∥AD， ∵OF=AD=2， ∴四边形OFDA为平行四边形， ∵∠OFD=90°， ∴平行四边形OFDA为矩形， ∴DA⊥AO， ∵正方形ABCD中，DA⊥AB， ∴O，A，B三点在同一条直线上； ∴EA⊥OB， ∵∠OEB=∠AOE， ∴△EOA∽△BOE， ∴， ∴OE2=OA•OB， ∴OA（2+OA）=4， 解得：OA=-1±， ∵OA＞0，∴OA=-1； 方法二： 在Rt△OAE中，cos∠EOA=， 在Rt△EOB中，cos∠EOB=， ∴， 解得：OA=-1±， ∵OA＞0，∴OA=-1； 方法三： ∵OE⊥EB，EA⊥OB， ∴由射影定理，得OE2=OA•OB， ∴OA（2+OA）=4， 解得：OA=-1±， ‎ ‎∵OA＞0， ∴OA=-1； （2）如图3，设∠MON=n°，S扇形MON=×22=n（cm2）， S随n的增大而增大，∠MON取最大值时，S扇形MON最大， 当∠MON取最小值时，S扇形MON最小， 如图，过O点作OK⊥MN于K，‎ ‎ ∴∠MON=2∠NOK，MN=2NK， 在Rt△ONK中，sin∠NOK=， ∴∠NOK随NK的增大而增大，∴∠MON随MN的增大而增大， ∴当MN最大时∠MON最大，当MN最小时∠MON最小， ①当N，M，A分别与D，B，O重合时，MN最大，MN=BD， ∠MON=∠BOD=90°，S扇形MON最大=π（cm2）， ②当MN=DC=2时，MN最小， ∴ON=MN=OM， ∴∠NOM=60°， S扇形MON最小=π（cm2）， ∴π≤S扇形MON≤π． 7、（1）连接AO、DO．设⊙O的半径为r．‎ 在Rt△ABC中，由勾股定理得AC==4，则⊙O的半径r=（AC+BC﹣AB）=（4+3﹣5）=1；‎ ‎∵CE、CF是⊙O的切线，∠ACB=90°，‎ ‎∴∠CFO=∠FCE=∠CEO=90°，CF=CE，‎ ‎∴四边形CEOF是正方形，‎ ‎∴CF=OF=1；‎ 又∵AD、AF是⊙O的切线，‎ ‎∴AF=AD；‎ ‎∴AF=AC﹣CF=AC﹣OF=4﹣1=3，即AD=3；‎ ‎（2）在Rt△ABC中，AB=5，AC=4，BC=3，‎ ‎∵∠C=90°，PH⊥AB，‎ ‎∴∠C=∠PHA=90°，‎ ‎∵∠A=∠A，‎ ‎∴△AHP∽△ACB，‎ ‎∴==，‎ 即=，‎ ‎∴y=﹣x+4，即y与x的函数关系式是y=﹣x+4；‎ ‎（3）如图，P′H′与⊙O相切．‎ ‎∵∠OMH′=∠MH′D=∠H′DO=90°，OM=OD，‎ ‎∴四边形OMH′D是正方形，‎ ‎∴MH′=OM=1；‎ 由（1）知，四边形CFOE是正方形，‎ CF=OF=1，‎ ‎∴P′H′=P′M+MH′=P′F+FC=P′C，即x=y；‎ 又由（2）知，y=﹣x+4，‎ ‎∴y=﹣y+4，解得，y=．‎ ‎8、（1）证明：连接OE FE、FA是⊙O的两条切线 ‎∴∠FAO=∠FEO=90°‎ 在Rt△OAF和Rt△OEF中，‎ ‎ ‎ ‎∴Rt△FAO≌Rt△FEO（HL），‎ ‎∴∠AOF=∠EOF=∠AOE，‎ ‎∴∠AOF=∠ABE，‎ ‎∴OF∥BE，‎ ‎（2）解：过F作FQ⊥BC于Q ‎∴PQ=BP﹣BQ=x﹣y PF=EF+EP=FA+BP=x+y ‎∵在Rt△PFQ中 ‎∴FQ2+QP2=PF2‎ ‎∴22+（x﹣y）2=（x+y）2‎ 化简得：，（1＜x＜2）；‎ ‎（3）存在这样的P点，‎ 理由：∵∠EOF=∠AOF，‎ ‎∴∠EHG=∠EOA=2∠EOF，‎ 当∠EFO=∠EHG=2∠EOF时，‎ 即∠EOF=30°时，Rt△EFO∽Rt△EHG，‎ 此时Rt△AFO中，‎ y=AF=OA•tan30°=，‎ ‎∴‎ ‎∴当时，△EFO∽△EHG．‎ ‎9、（1）PN与⊙O相切．‎ 证明：连接ON，‎ 则∠ONA=∠OAN，‎ ‎∵PM=PN，∴∠PNM=∠PMN．‎ ‎∵∠AMO=∠PMN，∴∠PNM=∠AMO．‎ ‎∴∠PNO=∠PNM+∠ONA=∠AMO+∠ONA=90°．‎ 即PN与⊙O相切．‎ ‎（2）成立．‎ 证明：连接ON，‎ 则∠ONA=∠OAN，‎ ‎∵PM=PN，∴∠PNM=∠PMN．‎ 在Rt△AOM中，‎ ‎∴∠OMA+∠OAM=90°，‎ ‎∴∠PNM+∠ONA=90°．‎ ‎∴∠PNO=180°﹣90°=90°．‎ 即PN与⊙O相切．‎ ‎（3）解：连接ON，由（2）可知∠ONP=90°．‎ ‎∵∠AMO=15°，PM=PN，∴∠PNM=15°，∠OPN=30°，‎ ‎∵∠PON=60°，∠AON=30°．‎ 作NE⊥OD，垂足为点E，‎ 则NE=ON•sin60°=1×=．‎ S阴影=S△AOC+S扇形AON﹣S△CON=OC•OA+CO•NE ‎=×1×1+π﹣×1×‎ ‎=+π﹣．‎ ‎10、（1）证明：∵△BCO中，BO=CO，‎ ‎∴∠B=∠BCO，‎ 在Rt△BCE中，∠2+∠B=90°，‎ 又∵∠1=∠2，∴∠1+∠BCO=90°，即∠FCO=90°，‎ ‎∴CF是⊙O的切线；‎ ‎（2）证明：∵AB是⊙O直径，∴∠ACB=∠FCO=90°，‎ ‎∴∠ACB﹣∠BCO=∠FCO﹣∠BCO，‎ 即∠3=∠1，∴∠3=∠2，‎ ‎∵∠4=∠D，∴△ACM∽△DCN；‎ ‎（3）解：∵⊙O的半径为4，即AO=CO=BO=4，‎ 在Rt△COE中，cos∠BOC=，‎ ‎∴OE=CO•cos∠BOC=4×=1，‎ 由此可得：BE=3，AE=5，由勾股定理可得：‎ CE===，‎ AC===2，‎ BC===2，‎ ‎∵AB是⊙O直径，AB⊥CD，‎ ‎∴由垂径定理得：CD=2CE=2，‎ ‎∵△ACM∽△DCN，‎ ‎∴=，‎ ‎∵点M是CO的中点，CM=AO=×4=2，‎ ‎∴CN===，‎ ‎∴BN=BC﹣CN=2﹣=．‎ ‎11、‎ ‎12、（1）如图4，过点O作OH⊥AP，那么AP＝2AH．‎ 在Rt△OAH中，OA＝3，，设OH＝m，AH＝2m，那么m2＋(2m)2＝32．‎ 解得．所以．‎ ‎（2）如图5，联结OQ、OP，那么△QPO、△OAP是等腰三角形．‎ 又因为底角∠P公用，所以△QPO∽△OAP．‎ 因此，即．‎ 由此得到．定义域是0＜x≤6．‎ 图4 图5‎ ‎（3）如图6，联结OP，作OP的垂直平分线交AP于Q，垂足为D，那么QP、QO是⊙Q的半径．‎ 在Rt△QPD中，，，因此．‎ 如图7，设⊙M的半径为r．‎ 由⊙M与⊙O内切，，可得圆心距OM＝3－r．‎ 由⊙M与⊙Q外切，，可得圆心距．‎ 在Rt△QOM中，，OM＝3－r，，由勾股定理，得 ‎．解得．‎ 图6 图7 图8‎