中考数学模拟试题-1 8页

数学中考模拟试题 说明：本试卷分第I 卷和第II卷，第I 卷为选择题卷，答在答题卡上；第II卷为非选择题卷，答在试题卷上.本试卷共五大题,25小题,时限：120分钟, 满分：120分.‎ Ⅰ卷 （选择题、填空题 共45分）‎ 一、选择题（每小题3分，共30分）‎ 下列各小题都给出了四个选项，其中只有一项是符合题目要求的，请把符合要求的选项前面的序号填写在Ⅱ卷上指定的位置 ‎1、下列展开图中，不是正方体是 A、 B、 C、 D、-‎ 题目简单更要仔细哟！‎ ‎2、实数a、b在数轴上的位置如图，下列结论正确的是 ‎ a b ‎ -1 0 1 ‎ A、a-b>0 B、a-b=0 C、|a-b|=b-a D、a+b=|a|+|b|‎ ‎3、下列各式计算错误的是 A、a2b+a2b=2a2b B、x+2x =3x C、a2b-3ab2=-2ab D、a2•a3=a5‎ ‎4、下列根式化简后被开方数是3的是 A、 B、 C、 D、 ‎ ‎5、△ABC的内切圆和外接圆是两个同心圆，那么△ABC一定是 A、等腰三角形 B、等边三角形 C、直角三角形 D、钝角三角形 ‎6、菱形具有而矩形不具有性质是 ‎ A、对角线相等 B、对角线互相平分 ‎ C、对角线互相垂直 D、对角线平分且相等 ‎7、随着我国三农问题的解决，小明家近两年的收入发生了变化。经测算前年棉花收入占48%，粮食收入占29%，副业收入占23%；去年棉花收入占36%，粮食收入占33%，副业收入占31%（如图）。下列说法正确的是 ‎②‎ ‎③‎ ‎③‎ ‎ ①棉花 ‎①‎ ‎ 前年 ②粮食 去年 ‎②‎ ‎①‎ ‎ ③副业 A、棉花收入前年的比去年多 B、粮食收入去年的比前年多 ‎ C、副业收入去年的比前年多 D、棉花收入哪年多不能确定 ‎8、下列图形中既是轴对称图形又是中心对称图形的是 C A、平行四边形 B、五角星 C、等边三角形 D、菱形 ‎9、 如图AB为半圆的直径，C为半圆上的一点，CD⊥AB于D，‎ 连接AC，BC，则与∠ACD互余有 ‎ B A D A、1个 B、 2个 C、3个 D、4个 ‎10、众志成城，预防“禽流感”。在这场没有硝烟的战斗中，科技工作者和医务人员通过探索，把某种药液稀释在水中进行喷洒，消毒效果较好，并且发现当稀释到某一浓度a时，效果最好而不是越浓越好。有一同学把效果与浓度的关系绘成曲线（如图），你认为正确的是 效果 效果 效果 效果 ‎ ‎ a 浓度 a 浓度 a 浓度 a 浓度 ‎ ‎ ‎ A B C D ‎ 二、填空题（每小题3分，共15分）‎ ‎11、把线段AB沿某一方向平移3个单位长,该线段移动前后和对应端点连线所组成的图形是 ‎ A B ‎ ‎ ‎ ‎ ‎ 12、受国际金融危机的影响，国际原油价格下跌。我国燃油价格也不例外。如汽油由原来的每升6元下跌到4.79元，若每升汽油0.75千克，那么现在一吨汽油的售价大约是 元。（精确到1）‎ D A ‎13、已知矩形ABCD的两边分别是关于x 的一元二次方程x2+mx+3=0的二根，则矩形ABCD的面积是 C B ‎14、外切两圆的半径分别是2和r，如果两圆的圆心距是6，则r是 ‎ ‎15、）观察16+9>2×4×3 ， 9+3>2×3× 那么3+2>2× ‎ ‎ ‎ 三、解答题（16~19题每题6分，共24分）‎ ‎16、计算：‎ ‎ a-2 + ‎ ‎ ‎ ‎17、如图，已知AC=DE，AF=DB，∠A=∠D，求证：BG=FG. 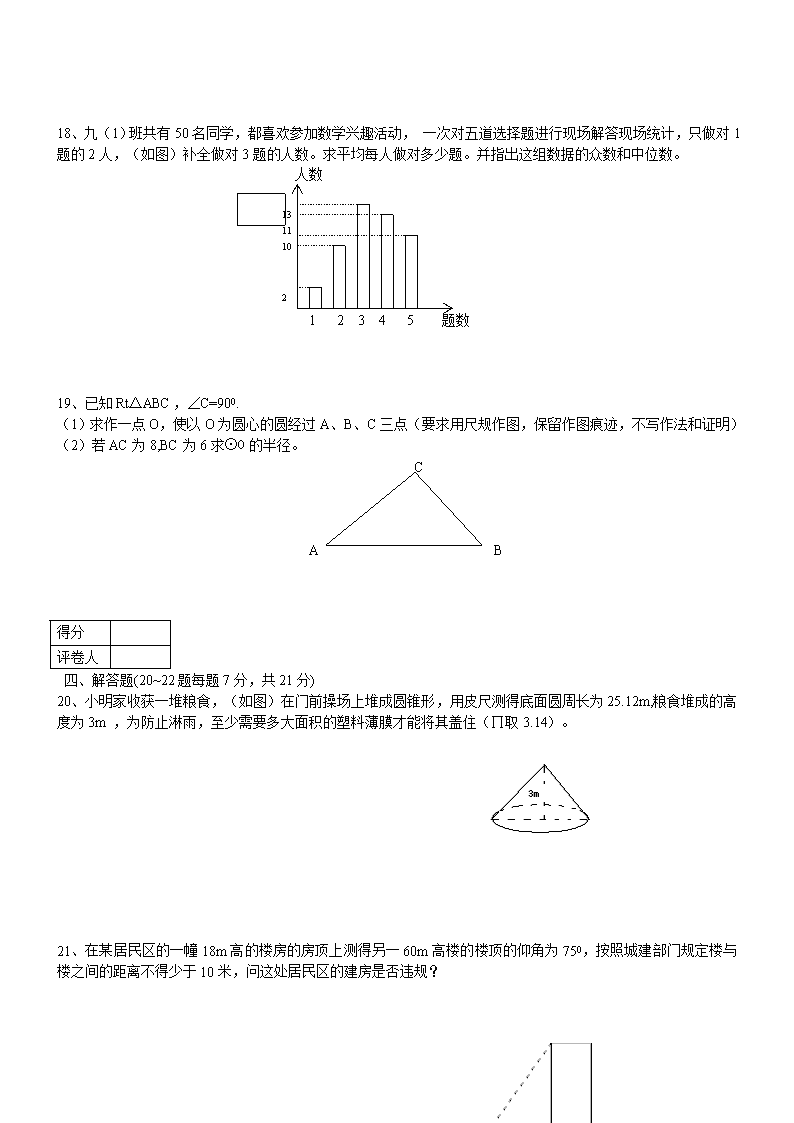‎ ‎18、九（1）班共有50名同学，都喜欢参加数学兴趣活动， 一次对五道选择题进行现场解答现场统计，只做对1题的2人，（如图）补全做对3题的人数。求平均每人做对多少题。并指出这组数据的众数和中位数。 人数 ‎13‎ ‎11‎ ‎10‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎2‎ ‎ ‎ ‎ 1 2 3 4 5 题数 ‎19、已知RtΔABC，∠C=900.‎ ‎（1）求作一点O，使以O为圆心的圆经过A、B、C三点（要求用尺规作图，保留作图痕迹，不写作法和证明）‎ ‎（2）若AC为8,BC为6求⊙O的半径。‎ ‎ C ‎ A B ‎ 得分 评卷人 ‎ 四、解答题(20~22题每题7分，共21分)‎ ‎20、小明家收获一堆粮食，（如图）在门前操场上堆成圆锥形，用皮尺测得底面圆周长为25.12m,粮食堆成的高度为3m ，为防止淋雨，至少需要多大面积的塑料薄膜才能将其盖住（∏取3.14）。 ‎ ‎21、在某居民区的一幢18m高的楼房的房顶上测得另一60m高楼的楼顶的仰角为750，按照城建部门规定楼与楼之间的距离不得少于10米，问这处居民区的建房是否违规？ ‎ ‎ ‎ ‎22、我们知道,利用两个转盘,做配紫色游戏。如图,红、蓝色区域各占一半，（1）求一个指针指向红，一个指针指向蓝配成紫色获胜的概率。（2）改变图2的红、蓝色区域比例使其扇形面积比为3﹕1 ，获胜的概率又是多少？由此，请进行猜想，写出你猜想的结果 ‎ 红 红 图2 ‎ 图1‎ ‎ ‎ ‎ ‎ 得分 评卷人 ‎ ‎ 五、解答题（23、24、25、每题各10分，共30分）‎ ‎23、把边长为1的正方形纸片沿对角线剪开，得⊿ABC和⊿DEF。‎ B F ‎（H）‎ G C D E A 然后，将⊿DEF的顶点D置于⊿ABC斜边中点处，使⊿DEF绕 点D沿顺时针旋转。‎ 图1‎ 图2‎ （1） 当⊿DEF旋转到DF过直角顶点C时（如图1）此时DF 与AC的交点H与点C重合，试判断∠DGB与∠DGH的关系，并 给以证明。‎ （2） 当⊿DEF继续旋转的角度为α（0<α<450）（如图2）‎ 时，（1）中A H G F E D C 的结论是否成立，若成立，请给以证明；若不成立，‎ 请说明理由。‎ B ‎ ‎ ‎24、随着人类对生态环境的破坏，造成近几年沙尘暴的频繁发生，引起了政府及其广大民众的警觉。就我市某县森林覆盖面从2004年到2006年通过进行调查研究，精确测算，2004年减少了5%，以后基本上每年减少的面积与前一年相同，照此计算（1）2006年森林覆盖面积是2004年的多少？（2）2006年投入了一定的劳力进行植树造林，结果只能保证该年森林覆盖面积不变，从2007年起到2008年止，共投入的劳力是上一年劳力的6.5倍，不考虑其它因素，如果每个劳力人均植树造林面积不变，问这两年森林的覆盖面积平均每年增长了百分之几？‎ ‎ ‎ ‎25、如图矩形OABC，AB=2OA=2n，分别以OA和OC为x、y轴建立平面直角坐标系，连接OB，沿OB折叠，使点A落在P处。过P作PQ⊥y轴于Q。‎ ‎（1）求OD:OA的值。‎ ‎（2）以B为顶点的抛物线：y=ax2+bx+c，经过点D，与直线 ‎ OB相交于E，过E作EF⊥y轴于F，试判断2·PQ·EF与 ‎ 矩形OABC面积的关系，并说明理由。‎ 数学中考模拟试题 参考答案 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 C C C C B C D D B B 题号 ‎11‎ ‎ 12‎ ‎ 13‎ ‎ 14‎ ‎ 15‎ 答案 平行四边形 ‎6387‎ ‎3‎ ‎4‎ ‎√6‎ ‎16、原式= 17、证△ACB≌△DEF即可 ‎18、补14，平均数3.42，众数和中位数分别是3、3；19、（1）略、（2）5‎ ‎20、r=4，l=5，s=62.8（cm2）；21、构造直角三角形，设两楼相距x 米，tan（900-750）= ，x=48tan250=11.25（米）符合要求。‎ ‎22、（1）p=0.5；（2）p=0.5。猜想：当一个转盘的红、蓝色区域各占一半时，无论怎样改变第二个转盘的红、蓝色区域所占的比例，获胜的概率都是0.5.‎ ‎23、（1）∠DGB=∠DGH ‎ 证明：在等腰Rt⊿ABC中，D是AB中点 ‎ ∴HD⊥AB，∴DH=1/2AB=DB ‎ ∵∠FDG=450=∠BDG, ∴DG⊥HB ‎ 因此∠DGB=∠DGH ‎ （2） （1）中的结论仍然成立。∠DGB=∠DGH ‎ 证明：连接DC,在BC上截取BI=CH ‎ ∵BI=CH, ∠DBI=∠DCH=450,DB=DC ‎ ∴⊿DBI≌⊿DCH, ∴DI=DH, ∠HDC=∠IDB,‎ ‎ ∴∠HDI=∠CDB=900,∵∠FDE=450=∠GDI,DG公共 ‎ ∴⊿DGH≌⊿DGI,∴∠DGB=∠DGH ‎24、（1）设2003年森林面积是m，则2004年为0.95m，2006年为0.85m，‎ ‎ 0.85m/0.95m=17/19‎ ‎ （2）2006年森林面积稳定为0.9m，投入的劳力植树造林面积为0.05m，2007年到2008年共投入的劳力植树造林面积为6.5×0.05m，设2007年到2008森林覆盖面积的增长率为x，由于2008年原有森林覆盖面积为0.9m-2×5%m则根据题意，得0.9m（1+x）2=6.5×0.05m+ 0.9m-2×5%m ‎ （1+x）2= x=± -1(负数舍去)‎ ‎ ∴x≈0.118‎ ‎25、(1)在矩形OABC中AB∥OC,∴∠ABO=∠BOC,根据题中的折叠得∠PBO=∠BOC ‎ ∴∠PBO=∠BOC, ∴BO=DO,设DO=k,则DB=k ‎ 在Rt⊿BCD中BC=n,DG=2n-k,BD=k ‎ ∴(2n-k)2+n2=k2, ∴OD=n,OD:OA=5/4‎ ‎ (2)设以B为顶点的抛物线为y=a(x-n)2+2n,把D(0, n)代入，得a=‎ ‎ ∴y=(x-n)2+2n==x2+x+n,直线OB为y=2x,二者联立，得 ‎ E(-n,- n), ∴EF=n,‎ ‎ 根据PQ⊥y轴于Q，∠BCO=900,得⊿BDC∽⊿PDQ,通过BD=OD=n,得PD=n ‎ ∴=== ∴PQ=n, ∴2·PQ·EF=2n2即矩形OABC面积