浙江宁波市2016年中考数学卷 11页

宁波市2016年初中毕业生学业考试 数 学 试 题 满分150分，考试时间120分钟 一、选择题（每小题4分，共48分，在每小题给出的四个选项中，只有一项符合题目要求）‎ ‎1. 6的相反数是 A. -6 B. C. D. 6‎ ‎2. 下列计算正确的是 A. B. C. D. ‎ ‎3. 宁波栎社国际机场三期扩建工程建设总投资84.5亿元，其中84.5亿元用科学计数法表示为 A. 0.845×1010元 B. 84.5×108元 C. 8.45×109元 D. 8.45×1010元 ‎4. 使二次根式有意义的的取值范围是 A. B. C. D. ‎ ‎5. 如图所示的几何体的主视图为 ‎6. 一个不透明布袋里装有1个白球、2个黑球、3个红球，它们除颜色外都相同。从中任意摸出一个球，是红球的概率为 A. B. C. D. ‎ ‎7. 某班10名学生校服尺寸与对应人数如下表所示：‎ 尺寸（cm）‎ ‎160‎ ‎165‎ ‎170‎ ‎175‎ ‎180‎ 学生人数（人）‎ ‎1‎ ‎3‎ ‎2‎ ‎2‎ ‎2‎ 则这10名学生校服尺寸的众数和中位数分别为 A. 165cm，165cm B. 165cm，170cm C. 170cm，165cm D. 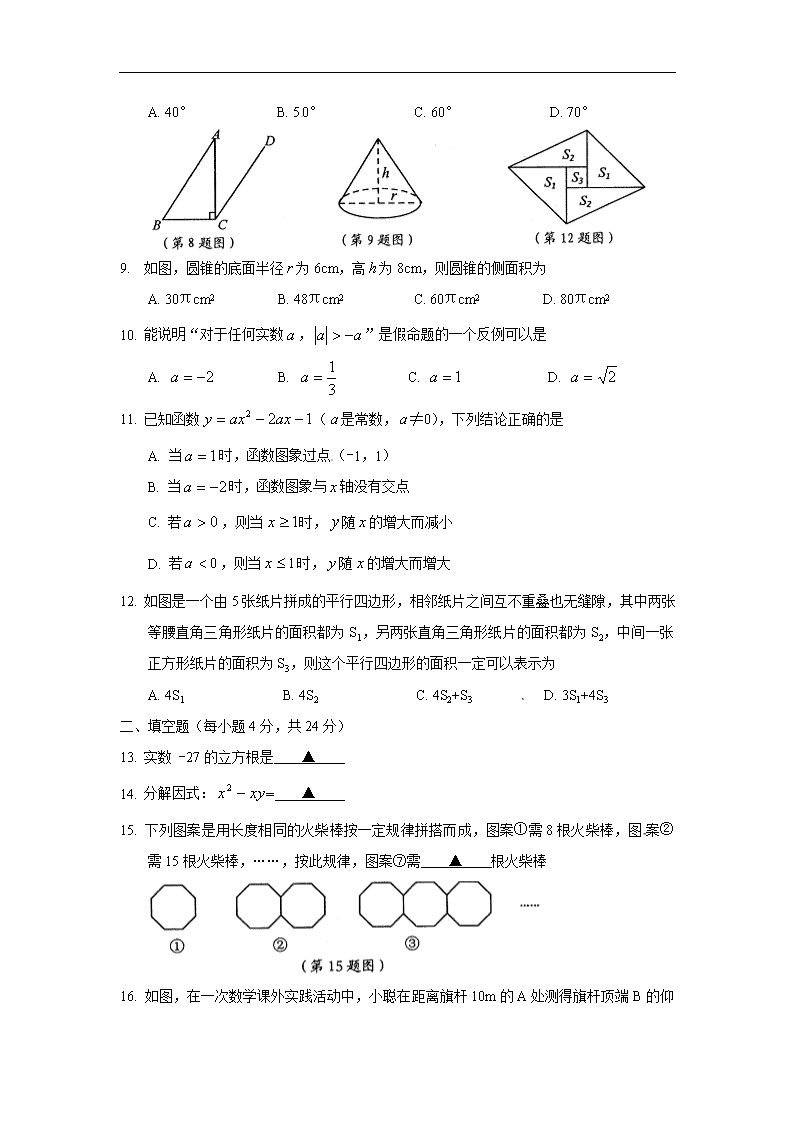170cm，170cm ‎8. 如图，在△ABC中，∠ACB=90°，CD∥AB，∠ACD=40°，则∠B的度数为 A. 40° B. 50° C. 60° D. 70°‎ ‎9. 如图，圆锥的底面半径为6cm，高为8cm，则圆锥的侧面积为 A. 30πcm2 B. 48πcm2 C. 60πcm2 D. 80πcm2‎ ‎10. 能说明“对于任何实数，”是假命题的一个反例可以是 A. B. C. D. ‎ ‎11. 已知函数（是常数，≠0），下列结论正确的是 A. 当时，函数图象过点（-1，1）‎ B. 当时，函数图象与轴没有交点 C. 若，则当时，随的增大而减小 D. 若，则当时，随的增大而增大 ‎12. 如图是一个由5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S1，另两张直角三角形纸片的面积都为S2，中间一张正方形纸片的面积为S3，则这个平行四边形的面积一定可以表示为 A. 4S1 B. 4S2 C. 4S2+S3 D. 3S1+4S3 ‎ 二、填空题（每小题4分，共24分）‎ ‎13. 实数 -27的立方根是 ▲ ‎ ‎14. 分解因式：= ▲ ‎ ‎15. 下列图案是用长度相同的火柴棒按一定规律拼搭而成，图案①需8根火柴棒，图案②需15根火柴棒，……，按此规律，图案⑦需 ▲ 根火柴棒 ‎16. ‎ 如图，在一次数学课外实践活动中，小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°，测角仪高AD为1m，则旗杆高BC为 ▲ m（结果保留根号）‎ ‎17. 如图，半圆O的直径AB=2，弦CD∥AB，∠COD=90°，则图中阴影部分面积为 ▲ ‎ ‎18. 如图，点A为函数图象上一点，连结OA，交函数的图象于点B，点C是轴上一点，且AO=AC，则△ABC的面积为 ▲ ‎ 三、解答题（本大题有8小题，共78分）‎ ‎19.（本题6分）先化简，再求值：，其中 ‎20.（本题8分）下列3×3网格都是由9个相同小正方形组成，每个网格图中有3个小正方形已涂上阴影，请在余下的6个空白小正方形中，按下列要求涂上阴影：‎ ‎（1）选取1个涂上阴影，使4个阴影小正方形组成一个轴对称图形，但不是中心对称图形；‎ ‎（2）选取1个涂上阴影，使4个阴影小正方形组成一个中心对称图形，但不是轴对称图形；‎ ‎（3）选取2个涂上阴影，使5个阴影小正方形组成一个轴对称图形。‎ ‎（请将三个小题依次作答在图1、图2、图3中，均只需画出符合条件的一种情形）‎ ‎21.（本题8分）为深化义务教育课程改革，某校 积极开展拓展性课程建设，设计开设艺术、体育、劳技、文学等多个类别的拓展性课程，要求每一位学生都自主选择一个类别的拓展性课程。为了了解学生选择拓展性课程的情况，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图（部分信息未给出）：‎ 根据统计图中的信息，解答下列问题：‎ ‎（1）求本次被调查的学生人数；‎ ‎（2）将条形图补充完整；‎ ‎（3）若该校共有1600名学生，请估计全校选择体育类的学生人数。‎ ‎22.（本题10分）如图，已知抛物线与轴交于A，B两点，与轴交于点C，点B的坐标为（3，0）。‎ ‎（1）求m的值及抛物线的顶点坐标；‎ ‎（2）点P是抛物线对称轴上的一个动点，当PA+PC的值最小时，求点P的坐标。‎ ‎23.（本题10分）如图，已知⊙O的直径AB=10，弦AC=6，‎ ‎∠BAC的平分线交⊙O于点D，过点D作DE⊥AC交AC的延长线于点E。‎ ‎（1）求证：DE是⊙O的切线；‎ ‎（2）求DE的长。‎ ‎24.（本题10分）某商场销售A，B两种品牌的教学设备，这两种教学设备的进价和售价如下表所示：‎ A B 进价（万元/套）‎ ‎1.5‎ ‎1.2‎ 售价（万元/套）‎ ‎1.65‎ ‎1.4‎ 该商场计划购进两种教学设备若干套，共需66万元，全部销售后可获毛利润9万元。‎ ‎（毛利润=（售价 - 进价）×销售量）‎ ‎（1）该商场计划购进A，B两种品牌的教学设备各多少套？‎ ‎（2）通过市场调研，该商场决定在原计划的基础上，减少A种设备的购进数量，增加B种设备的购进数量，已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元，问A种设备购进数量至多减少多少套？‎ ‎25.（本题12分）从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中有一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线。‎ ‎（1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线；‎ ‎（2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数；‎ ‎（3）如图2，△ABC中，AC=2，BC=，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长。‎ ‎26.（本题14分）如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（5‎ ‎，0），菱形OABC的顶点B，C在第一象限，tan∠AOC=，将菱形绕点A按顺时针方向旋转角α（0°<α<∠AOC）得到菱形FADE（点O的对应点为点F），EF与OC交于点G，连结AG。‎ ‎（1）求点B的坐标；‎ ‎（2）当OG=4时，求AG的长；‎ ‎（3）求证：GA平分∠OGE；‎ ‎（4）连结BD并延长交轴于点P，当点P的坐标为（12，0）时，求点G的坐标。‎ ‎ ‎