中考圆大题专题复习本人 6页

常考问题：一、证切线 ‎ 方法：連半径、证垂直。难点：证角，处理技巧一用平行线，二用互余、三用边角、弧角转换，‎ ‎ 二、考查三角函数，‎ ‎ 方法：注意转换角所在三角形，很多时候给出的三角函数没有直角三角形，要想办法转换到另 ‎ ‎ 一个直角三角形去。‎ ‎ 三、求线段长 ‎ 方法：有三角函数的题可以考虑用三角函数求边长 ‎ 没有三角函数的考虑相似三角形和勾股定理 相似三角形的模型：‎ ‎ 四、求面积 ‎ 方法：一是利用相似，二是利用割补法 ‎1、（08年20题）．如图8，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且AB＝AD＝AO．‎ ‎（1）求证：BD是⊙O的切线．‎ ‎（2）若点E是劣弧BC上一点，AE与BC相交于点F，‎ 且△BEF的面积为8，cos∠BFA＝，求△ACF的面积．‎ ‎2、（09年21题）．（本题8分）如图10，AB是⊙O的直径，AB=10，‎ 图10‎ DC切⊙O于点C，AD⊥DC，垂足为D，AD交⊙O于点E。‎ ‎（1）求证：AC平分∠BAD；（4分）‎ ‎（2）若sin∠BEC=，求DC的长。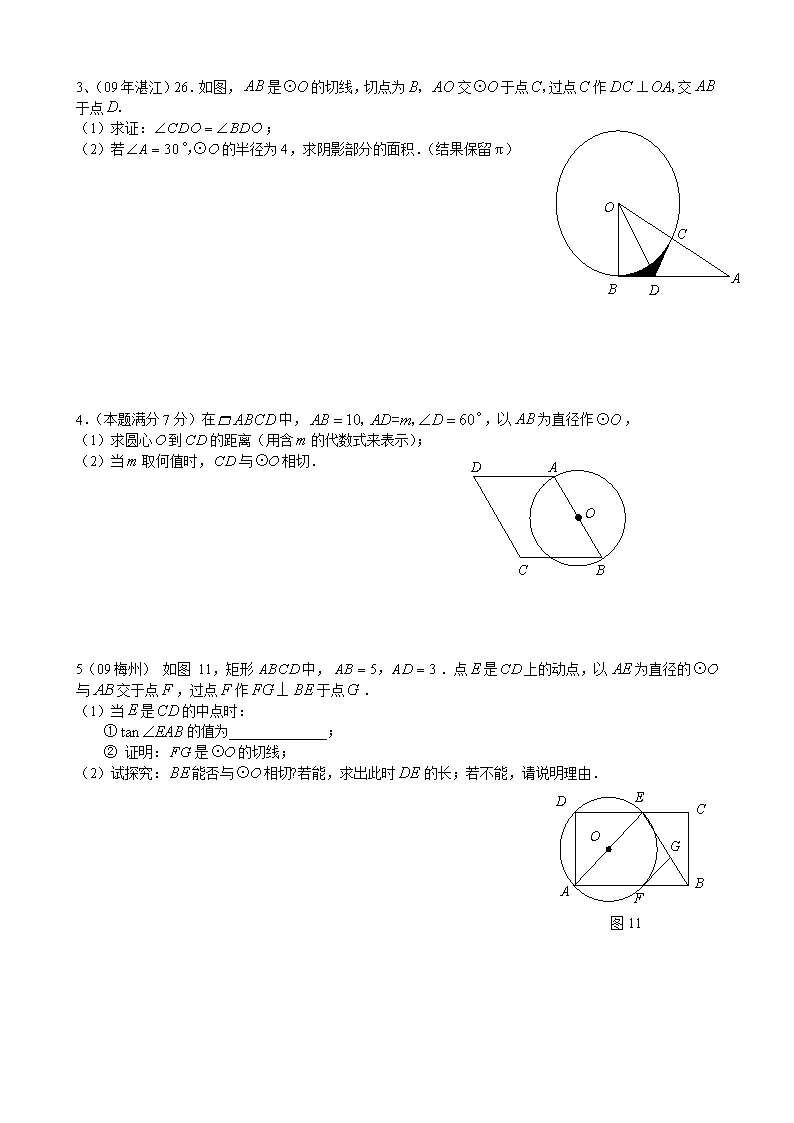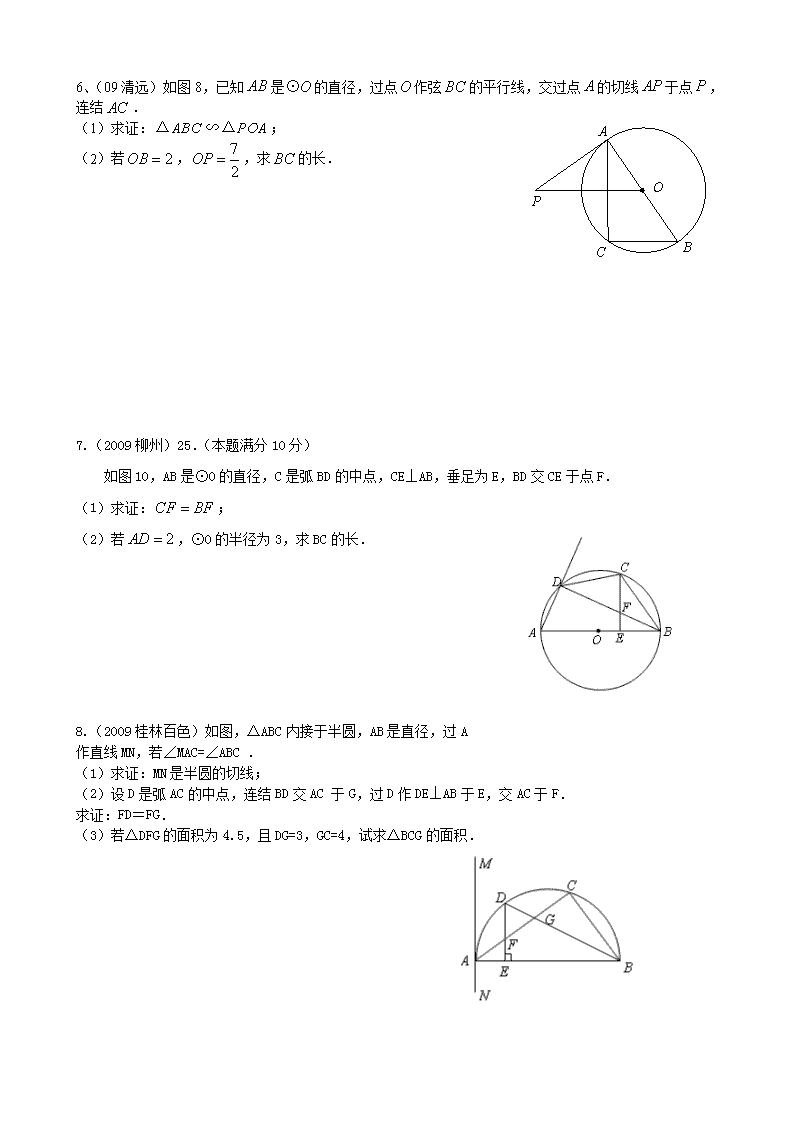（4分 ‎3、（09年湛江）26．如图，是的切线，切点为交于点过点作交于点 O A B C D ‎（1）求证：；‎ ‎（2）若的半径为4，求阴影部分的面积．（结果保留）‎ ‎4．（本题满分7分）在中，，以为直径作，‎ A D B C O ‎（1）求圆心到的距离（用含的代数式来表示）；‎ ‎（2）当取何值时，与相切．‎ ‎5（09梅州） 如图 11，矩形中，．点是上的动点，以为直径的与交于点，过点作于点． ‎ ‎（1）当是的中点时： ‎ ‎①的值为______________； ‎ ‎② 证明：是的切线； ‎ ‎（2）试探究：能否与相切?若能，求出此时的长；若不能，请说明理由．‎ D E O C B G F A 图11‎ ‎6、（09清远）如图8，已知是的直径，过点作弦的平行线，交过点的切线于点，连结．‎ P O A C B ‎（1）求证：；‎ ‎（2）若，，求的长．‎ ‎7.（2009柳州）25．（本题满分10分）‎ 如图10，AB是⊙O的直径，C是弧BD的中点，CE⊥AB，垂足为E，BD交CE于点F．‎ ‎（1）求证：；‎ ‎（2）若，⊙O的半径为3，求BC的长． ‎ ‎8.（2009桂林百色）如图，△ABC内接于半圆，AB是直径，过A 作直线MN，若∠MAC=∠ABC ．‎ ‎（1）求证：MN是半圆的切线；‎ ‎（2）设D是弧AC的中点，连结BD交AC 于G，过D作DE⊥AB于E，交AC于F． ‎ 求证：FD＝FG．‎ ‎（3）若△DFG的面积为4.5，且DG=3，GC=4，试求△BCG的面积．‎ ‎9(2009年本溪)22．如图所示，AB是直径，弦于点，且交于点，若．‎ ‎（1）判断直线和的位置关系，并给出证明；‎ ‎（2）当时，求的长．‎ ‎10．(2009年南充)如图8，半圆的直径，点C在半圆上，．‎ ‎（1）求弦的长；‎ ‎（2）若P为AB的中点，交于点E，求的长．‎ P B C E A ‎11. （2009年株洲市）（本题满分10分）如图，点、、是上的三点，.‎ ‎（1）求证：平分.‎ ‎（2）过点作于点，交于点. 若，，求的长．‎ ‎12.(2009年达州)如图10，⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E，AC∥‎ DE交BD于点H，DO及延长线分别交AC、BC于点G、F.‎ ‎(1)求证：DF垂直平分AC；‎ ‎（2）求证：FC＝CE；‎ ‎（3）若弦AD＝5㎝，AC＝8㎝，求⊙O的半径. ‎ ‎13、 （2009年广西梧州）如图（8）所示，△ABC内接于⊙O，AB是⊙O的直径，点D在⊙O 上，过点C的切线交AD的延长线于点E，且AE⊥CE，连接CD．‎ ‎（1）求证：DC=BC；‎ ‎（2）若AB=5，AC=4，求tan∠DCE的值．‎ ‎14.（2009年包头）如图，已知是的直径，点在上，过点的直线与的延长线交于点，，．‎ ‎（1）求证：是的切线；‎ ‎（2）求证：；‎ ‎（3）点是的中点，交于点，若，求的值．‎ ‎15.（2009年长沙）在中，，是边上一点，以为直径的与边相切于点，连结并延长，与的延长线交于点．‎ ‎（1）求证：；‎ ‎（2）若，求的面积．‎