中考数学真题解析一次函数与反比例函数的综合应用含答案 79页

全国中考真题解析 一次函数与反比例函数的综合应用 一、选择题 1. （2011 四川凉山，12，4 分）二次函数 的图象如图所示，反比列函数 与正比列函数 在同一坐标系内的大致图象是（ ） 2. （2011•青海）一次函数 y=﹣2x+1 和反比例函数 y= 的大致图象是（　　） A、 B、 C、 D、 3. （2011 山东青岛，8，3 分）已知一次函数 y1=kx+b 与反比例函数 y2= 在同一直角坐标 系中的图象如图所示，则当 y1＜y2 时，x 的取值范围是（　　） A．x＜﹣1 或 0＜x＜3 B．﹣1＜x＜0 或 x＞3 C．﹣1＜x＜0 D．x＞3 （2011 杭州，6，3 分）如图，函数 y 1=x-1 和函数 y2=2x 的图象相交于点 M（2，m），N （-1，n），若 y1＞y2，则 x 的取值范围是（　　） 2y ax bx c= + + ay x = y bx= 第 12 题 O x y O y x A O y x B O y x D O y x C k x A．x＜-1 或 0＜x＜2 B．x＜-1 或 x＞2 C．-1＜x＜0 或 0＜x＜2 D．-1＜x＜0 或 x＞2 4.（2011 浙江台州，9，4 分）如图，双曲线 y= 与直线 y=kx+b 交于点 M．N，并且点 M 的坐标为（1，3），点 N 的纵坐标为﹣1．根据图象信息可得关于 x 的方程 =kx+b 的解为 （　　） A．﹣3，1 B．﹣3，3 C．﹣1，1 D．﹣1，3 5. （2011•丹东，6，3 分）反比例函数 y= 的图象如图所示，则一次函数 y=kx+k 的图象大 致是（　　） A、 B、 C、 D、 6. （2011•宜昌，15，3 分）如图，直线 y=x+2 与双曲线 y= 在第二象限有两个交点， 那么 m 的取值范围在数轴上表示为（　　） 考点：反比例函数与一次函数的交点问题；在数轴上表示不等式的解集。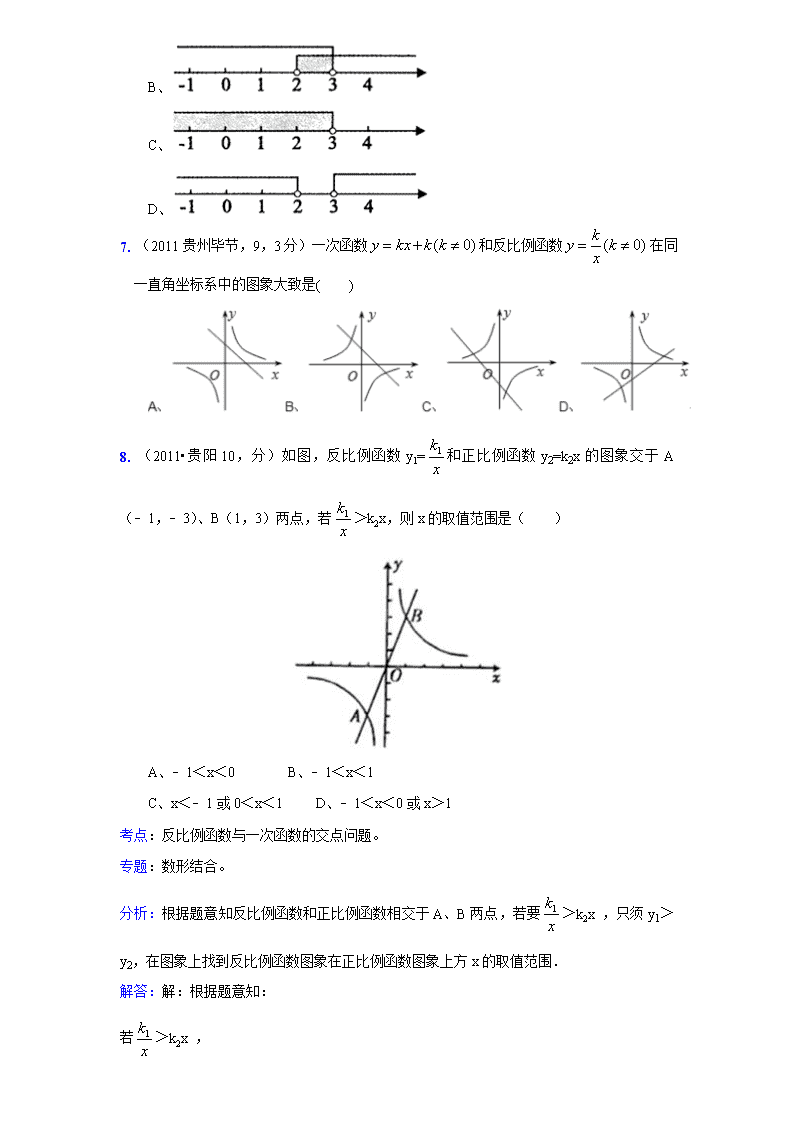 A、 m x m x x k 3m x − B、 C、 D、 7. （2011 贵州毕节，9，3 分）一次函数 和反比例函数 在同 一直角坐标系中的图象大致是( ) 8. （2011•贵阳 10，分）如图，反比例函数 y 1= 和正比例函数 y2=k2x 的图象交于 A （﹣1，﹣3）、B（1，3）两点，若 ＞k2x，则 x 的取值范围是（　　） A、﹣1＜x＜0 B、﹣1＜x＜1 C、x＜﹣1 或 0＜x＜1 D、﹣1＜x＜0 或 x＞1 考点：反比例函数与一次函数的交点问题。 专题：数形结合。 分析：根据题意知反比例函数和正比例函数相交于 A、B 两点，若要 ＞k2x ，只须 y1＞ y2，在图象上找到反比例函数图象在正比例函数图象上方 x 的取值范围． 解答：解：根据题意知： 若 ＞k2x ， )0( ≠+= kkkxy )0( ≠= kx ky x k1 x k1 x k1 x k1 则只须 y1＞y2， 又知反比例函数和正比例函数相交于 A、B 两点， 从图象上可以看出当 x＜﹣1 或 0＜x＜1 时 y1＞y2， 故选 C． 点评：本题主要考查了待定系数法求反比例函数与一次函数的解析式和反比例函数 y= 中 k 的几何意义．这里体现了数形结合的思想，做此类题一定要正确理解 k 的几何意义． 9. （2011 广东湛江,12,3 分）在同一坐标系中，正比例函数 y=x 与反比例函数 的图象 大致是（　　） A、 B、 C、 D、 考点：反比例函数的图象；一次函数的图象． 分析：根据正比例函数与反比例函数图象的性质进行选择即可． 解答：解：∵正比例函数 y=x 中，k=1＞0， ∴此图象过一、三象限； ∵反比例函数 中，k=2＞0， ∴此函数图象在一、三象限． 故选 B． 点评：此题主要考查了反比例函数的图象性质和一次函数的图象性质，要掌握它们的性质才 能灵活解题． 10.（2011 广西百色，10，4 分）二次函数的图象如图，则反比例函数 y=﹣ 与一次函数 y=bx+c 的图象在同一坐标系内的图象大致是（　　） A． B． x k 2y x = 2y x = x a C． D． 考点：二次函数的图象；一次函数的图象；反比例函数的图象． 分析：根据二次函数的图象，推出 a＜0，c＜0，顶点坐标都为正值，即可推出，b＞0，﹣a ＞0，根据反比例函数和一次函数的图形的性质推出反比例函数在第一、三象限，一次函数 经过第一、三，四象限，所以图象大致为 B 项中的图象． 解答：解：∵二次函数图象的开口向下， ∴a＜0， ∵顶点坐标都为正值， ∴ ＞0， ∴b＞0， ∴﹣a＞0， ∴反比例函数在第一、三象限，一次函数经过第一、三、四象限． 故选 B． 点评：本题主要考查反比例函数的图象的性质．二次函数图象的性质．反比例函数图象的性 质，关键在于通过二次函数图象推出 a、b 的取值范围． 11. （2011•恩施州 5,3 分）一次函数 y1=k1x+b 和反比例函数 y2= （k1∙k2≠0）的图象如图 所示，若 y1＞y2，则 x 的取值范围是（　　） A、﹣2＜x＜0 或 x＞1 B、﹣2＜x＜1 C、x＜﹣2 或 x＞1 D、x＜﹣2 或 0＜x＜1 考点：反比例函数与一次函数的交点问题。 专题：数形结合。 分析：根据图象可以知道一次函数 y1=k1x+b 和反比例函数 y2= （k1∙k2≠0）的图象的交点 的横坐标，若 y1＞y2，则根据图象可以确定 x 的取值范围． a b 2 − x k2 x k2 解答：解：如图，依题意得一次函数 y1=k1x+b 和反比例函数 y2= （k1∙k2≠0）的图象的交 点的横坐标分别为 x=﹣2 或 x=1， 若 y1＞y2，则 y1 的图象在 y2 的上面， x 的取值范围是﹣2＜x＜0 或 x＞1． 故选 A． 点评：此题主要考查了反比例函数与一次函数的图象的交点问题，解题的关键是利用数形结 合的方法解决问题． 12.（2011 年山东省东营市，10，3 分）如图，直线 l 和双曲线 交于 A、B 两点， P 是线段 AB 上的点（不与 A、B 重合），过点 A、B、P 分别向 x 轴作垂线，垂足分别为 C、D、E，连接 OA、OB、0P，设△AOC 的面积为 S1、△BOD 的面积为 S2、△POE 的面积 为 S3，则（　　） A、S1＜S2＜S3 B、S1＞S2＞S3 C、S1=S2＞S3 D、S1=S2＜S3 考点：反比例函数系数 k 的几何意义；反比例函数与一次函数的交点问题． 专题：几何图形问题． 分析：根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角 三角形面积 S 的关系即 S= |k|． 解答：解：结合题意可得：AB 都在双曲线 y= 上， 则有 S1=S2； 而 AB 之间，直线在双曲线上方； 故 S1=S2＜S3． 故选 D． 点评：本题主要考查了反比例函数 y= 中 k 的几何意义，即过双曲线上任意一点引 x 轴、y 轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此 类题一定要正确理解 k 的几何意义． 13. （2011 陕西，8，3 分）如图，过 y 轴正半轴上的任意一点 P，作 x 轴的平行线，分别与 x k2 ( 0)ky kx = ＞ 1 2 k x k x 反比例函数 的图象交于点 A 和点 B，若点 C 是 x 轴上任意一点，连接 AC、 BC，则△ABC 的面积为 （ ） A．3 B．4 C．5 D．6 考点：反比例函数综合题。 专题：计算题。 分析：先设 P（0，b），由直线 APB∥x 轴，则 A，B 两点的纵坐标都为 b，而 A，B 分别在 反比例函数 的图象上，可得到 A 点坐标为（﹣ ，b），B 点坐标为 （ ，b），从而求出 AB 的长，然后根据三角形的面积公式计算即可． 解答：解：设 P（0，b），∵直线 APB∥x 轴，∴A，B 两点的纵坐标都为 b，而点 A 在反比例 函数 y=﹣ 的图象上，∴当 y=b，x=﹣ ，即 A 点坐标为（﹣ ，b），又∵点 B 在反比例 函数 y= 的图象上，∴当 y=b，x= ，即 B 点坐标为（ ，b），∴AB= ﹣（﹣ ）= ，∴S△ABC= •AB•OP= •b=3． 故选 A． 点评：本题考查了点在函数图象上，点的横纵坐标满足函数图象的解析式．也考查了与坐标 轴平行的直线上的点的坐标特点以及三角形的面积公式． 二、填空题 1. （2011 江苏南京，15，2 分）设函数 y= 与 y=x﹣1 的图象的交点坐标为（a，B），则 的值为　﹣ ． 考点：反比例函数与一次函数的交点问题。 专题：计算题。 分析：把交点坐标代入 2 个函数后，得到 2 个方程，求得 a，B 的解，整理求得 ﹣ 的值即 可． 解答：解：∵函数 y= 与 y=x﹣1 的图象的交点坐标为（a，B）， xyxy 24 =−= 和 xyxy 24 =−= 和 2 x 1 1 a b − 1 2 2 x ∴B= ，B=a﹣1， ∴ =a﹣1， a2﹣a﹣2=0， （a﹣2）（a+1）=0， 解得 a=2 或 a=﹣1， ∴B=1 或 B=﹣2， ∴则 的值为 ． 故答案为： ． 点评：考查函数的交点问题；得到 2 个方程判断出 a，B 的值是解决本题的关键． 2. （2011 江苏苏州，18，3 分）如图，已知点 A 的坐标为（ ，3），AB 丄 x 轴，垂足为 B，连接 OA，反比例函数 （k＞0）的图象与线段 OA、AB 分别交于点 C、D．若 AB=3BD， 以点 C 为圆心，CA 的 倍的长为半径作圆，则该圆与 x 轴的位置关系是__________（填” 相离”，“相切”或“相交“）． 考点：直线与圆的位置关系；反比例函数图象上点的坐标特征． 分析：根据 D 点的坐标为（ ，1），得出反比例函数 解析式，再根据 A 点坐标得出 AO 直线解析式，进而得出两图象的交点坐标，进而得出 AC 的长度，再利用直线与圆的位 置关系得出答案． 解答：解：∵已知点 A 的坐标为（ ，3），AB=3BD， ∴AB=3，BD=1， ∴D 点的坐标为（ ，1）， ∴反比例函数 解析式为： 2 a 2 a 1 1 a b − 1 2 1 2 3 ky x = 5 4 3 ky x = 3 3 ky x = y= ， ∴AO 直线解析式为：y=kx， 3= k， ∴k= ， ∴y= x， ∴直线 y= x 与反比例函数 y= 的交点坐标为： x=±1， ∴C 点的横坐标为 1， 纵坐标为： ， CO=2， ∴AC=2 -2， ∴CA 的 倍= ， CE= ， ∵ - = ＞0， ∴该圆与 x 轴的位置关系是相交． 故答案为：相交． 点评：此题主要考查了直线与圆的位置关系以及反比例函数的性质以及直线与反比例函数交 点坐标的求法，综合性较强得出 AC 的长是解决问题的关键． 3. （2011 湖北荆州，16，3 分）如图，双曲线 y=2x （x＞0）经过四边形 OABC 的顶点 A、 C，∠ABC=90°，OC 平分 OA 与 x 轴正半轴的夹角，AB∥x 轴．将△ABC 沿 AC 翻折后得 AB′C，B′点落在 OA 上，则四边形 OABC 的面积是 2． 3 x 3 3 3 3 3 x 3 3 5 4 5 ( 3 1)2 − 5 ( 3 1)2 − 3 3 532 2 − 考点：反比例函数综合题；翻折变换（折叠问题）． 专题：计算题． 分析：延长 BC，交 x 轴于点 D，设点 C（x，y），AB=a，由角平分线的性质得，CD=CB′， 则△OCD≌△OCB′，再由翻折的性质得，BC=B′C，根据反比例函数的性质，可得出 S△OCD= 12xy， 则 S△OCB′= 12xy，由 AB∥x 轴，得点 A（x-a，2y），由题意得 2y（x-a）=2，从而得出三角 形 ABC 的面积等于 12ay，即可得出答案． 解答：解：延长 BC，交 x 轴于点 D， 设点 C（x，y），AB=a， ∵OC 平分 OA 与 x 轴正半轴的夹角， ∴CD=CB′，△OCD≌△OCB′， 再由翻折的性质得，BC=B′C， ∵双曲线 y=2x （x＞0）经过四边形 OABC 的顶点 A、C， ∴S△OCD= 12xy=1， ∴S△OCB′= 12xy=1， ∵AB∥x 轴， ∴点 A（x-a，2y）， ∴2y（x-a）=2， ∴ay=1， ∴S△ABC= 12ay= 12， ∴SOABC=S△OCB′+S△ABC+S△ABC=1+ 12+ 12=2． 故答案为：2． 点评：本题是一道反比例函数的综合题，考查了翻折的性质、反比例函数的性质以及角平分 线的性质，是中考压轴题，难度偏大． 4.（2011 广西崇左，8，2 分）若一次函数的图象经过反比例函数 图象上的两点（1， m）和（n，2），则这个一次函数的解析式是　 　． 考点：待定系数法求一次函数解析式；反比例函数图象上点的坐标特征． 分析：一次函数的图象经过反比例函数 图象上的两点（1，m）和（n，2），先 代入求出 m，n 的值，再用待定系数法可求出函数关系式． 解答：解：（1，m）和（n，2）在函数 图象上，因而满足函数解析式， 代入就得到 m=﹣4，n=﹣2， 因而点的坐标是（1，4）和（﹣2，2）， 设直线的解析式是 y=kx+b， 根据题意得到 ， 解得 ． 因而一次函数的解析式是 ． 点评：本题主要考查了函数解析式与图象的关系，函数的图象上的点满足函数解析式， 反之，满足解析式的点一定在函数的图象上． 5.（2011 湖北黄石，15,3 分）若一次函数 y=kx+1 的图象与反比例函数 的图象没有公 共点，则实数 k 的取值范围是 ． 考点：反比例函数与一次函数的交点问题。 专题：计算题；数形结合。 分析：因为反比例函数 的图象在第一、三象限，故一次函数 y=kx+b 中，k＜0，解方 程组 求出当直线与双曲线只有一个交点时，k 的值，再确定无公共点时 k 的取值 范围． 解答：解：由反比例函数的性质可知， 的图象在第一、三象限， ∴当一次函数 y=kx+1 与反比例函数图象无交点时，k＜0， 解方程组 ，得 kx2+x﹣1=0， 当两函数图象只有一个交点时，△=0，即 1+4k=0，解得 ， xy 4−= xy 4−= xy 4−=    =+− =+ 22 4 bk bk      = −= 3 14 3 2 b k 3 14 3 2 +−= xy xy 1= 04 1 <<− k xy 1=    = += xy bkxy 1 xy 1=    = += xy bkxy 1 4 1−=k ∴两函数图象无公共点时， ． 故答案为： ． 点评：本题考查了反比例函数与一次函数的交点问题．关键是根据形数结合，判断无交点时， 图象的位置与系数的关系，找出只有一个交点时 k 的值，再确定 k 的取值范围． 6.（2011 成都，25，4 分）在平面直角坐标系 xOy 中，已知反比例函数 ( )满足： 当 x＜0 时，y 随 x 的增大而减小．若该反比例函数的图象与直线 都经过点 P， 且 ，则实数 ． 考点：反比例函数与一次函数的交点问题。 专题：计算题。 分析：由反比例函数 y＝ 当 x＜0 时，y 随 x 的增大而减小，可判断 k＞0，设 P（x，y）， 则 P 点坐标满足反比例函数与一次函数解析式，即 xy＝2k，x＋y＝ k，又 OP2＝x2＋y2， 将已知条件代入，列方程求解． 解答：解：∵反比例函数 y＝ 当 x＜0 时，y 随 x 的增大而减小，∴k＞0， 设 P（x，y），则 xy＝2k，x＋y＝ k， 又∵OP2＝x2＋y2， ∴x2＋y2＝7，即（x＋y）2－2xy＝7， （ k）2－4k＝7， 解得 k＝ 或－1，而 k＞0， ∴k＝ ． 故答案为： ． 点评：本题考查了反比例函数与一次函数的交点问题．关键是根据交点坐标满足反比例函 数．一次函数解析式，列方程组求解． 7.（2011•包头，18，3 分）如图，已知 A（﹣1，m）与 B（2，m+3 ）是反比例函数 y= 的图象上的两个点，点 C 是直线 AB 与 x 轴的交点，则点 C 的坐标是　（1，0）　． 04 1 <<− k 04 1 <<− k x ky 2= 0≠k kxy 3+−= 7=OP 3 7=k x k2 3 x k2 3 3 3 7 3 7 3 7 3 考点：反比例函数与一次函数的交点问题。 专题：计算题。 分析：根据反比例函数的性质，横纵坐标的乘积为定值，可得出关于 k、m 的两个方程，即 可得出反比例函数的解析式，从而得出点 C 的坐标． 解答：解：∵A（﹣1，m）与 B（2，m+3 ）是反比例函数 y= 的图象上的两个点， ∴ ，解得 k=2 ，m=﹣2 ， ∴A（﹣1，﹣2 ）与 B（2， ） 设直线 AB 的解析式为 y=ax+b， ∴ ，∴ ， ∴直线 AB 的解析式为 y= x﹣ ， 令 y=0，解得 x=1， ∴点 C 的坐标是（1，0）． 故答案为（1，0）． 点评：本题考查了反比例函数和一次函数的交点问题，能够熟练运用待定系数法求得函数的 解析式；求一次函数和 x 轴的交点坐标． 8. （2011 浙江宁波，18，3）正方形的 A1B1P1P2 顶点 P1、P2 在反比例函数 y＝ （x＞0） 的图象上，顶点 A1、B1 分别在 x 轴、y 轴的正半轴上，再在其右侧作正方形 P2P3A2B2，顶 点 P3 在反比例函数 y＝ （x＞0）的图象上，顶点 A2 在 x 轴的正半轴上，则点 P3 的坐标 为　（ +1， －1）．　． A B CO x y 3    =+ =− km km )33(2 3 3 3 3    =+ −=+− 32 32 ba ba    −= = 3 3 b a 3 3 x 2 x 2 3 3 考点：反比例函数综合题。 专题：综合题。 分析：作 P1⊥y 轴于 C，P2⊥x 轴于 D，P3⊥x 轴于 E，P3⊥P2D 于 F，设 P1（a， ），则 CP1＝ a，OC＝ ，易得 Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D，则 OB1＝P1C＝A1D＝a，所以 OA1＝ B1C＝P2D＝ －a，则 P2 的坐标为（ ， －a），然后把 P2 的坐标代入反比例函数 y＝ ， 得 到 a 的 方 程 ， 解 方 程 求 出 a ， 得 到 P2 的 坐 标 ； 设 P3 的 坐 标 为 （ b ， ），易 得 Rt△P2P3F≌Rt△A2P3E，则 P3E＝P3F＝DE＝ ，通过 OE＝OD+DE＝2+ ＝b，这样得到关 于 b 的方程，解方程求出 b，得到 P3 的坐标． 解答：解：作 P1⊥y 轴于 C，P2⊥x 轴于 D，P3⊥x 轴于 E，P3⊥P2D 于 F，如图， 设 P1（a， ），则 CP1＝a，OC＝ ， ∵四边形 A1B1P1P2 为正方形， ∴Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D， ∴OB1＝P1C＝A1D＝a， ∴OA1＝B1C＝P2D＝ －a，∴OD＝a+ －a＝ ， ∴P2 的坐标为（ ， －a）， 把 P2 的坐标代入 y＝ （x＞0），得到（ －a）• ＝2，解得 a＝－1（舍）或 a＝1， ∴P2（2，1）， 设 P3 的坐标为（b， ）， 又∵四边形 P2P3A2B2 为正方形， ∴Rt△P2P3F≌Rt△A2P3E， a 2 a 2 a 2 a 2 a 2 x 2 b 2 b 2 b 2 a 2 a 2 a 2 a 2 a 2 a 2 a 2 x 2 a 2 a 2 b 2 ∴P3E＝P3F＝DE＝ ，∴OE＝OD+DE＝2+ ， ∴2+ ＝b，解得 b＝1－ （舍），b＝1+ ，∴ ＝ ＝ －1， ∴点 P3 的坐标为 （ +1， －1）． 故答案为：（ +1， －1）． 点评：本题考查了反比例函数图象上点的坐标特点为横纵坐标之积为定值；也考查了正方形 的性质和三角形全等的判定与性质以及解分式方程的方法． 9. （2011 浙江衢州，15，4 分）在直角坐标系中，有如图所示的 Rt△ABO，AB⊥x 轴于点 B， 斜边 AO=10，sin∠AOB= ，反比例函数 的图象经过 AO 的中点 C，且与 AB 交 于点 D，则点 D 的坐标为　（8， ）　． 考点：反比例函数综合题。 专题：综合题。 分析：由斜边 AO=10，sin∠AOB= ，根据三角函数的定义可得到 AB=6，再由勾股定理得到 OB=8，即得到 A 点坐标为（8，6），从而得到 AO 的中点 C 的坐标，代入反比例函数解析式 确定 k，然后令 x=8，即可得到 D 点的纵坐标． 解答：解：∵斜边 AO=10，sin∠AOB= ， ∴sin∠AOB= ， ∴AB=6， ∴OB= =8， ∴A 点坐标为（8，6）， 而 C 点为 OA 的中点， ∴C 点坐标为（4，3）， 又∵反比例函数 的图象经过点 C， ∴k=4×3=12，即反比例函数的解析式为 y= ， ∵D 点在反比例函数的图象上，且它的横坐标为 8， ∴当 x=8，y= = ， 所以 D 点坐标为（8， ）． b 2 b 2 b 2 3 3 b 2 31 2 + 3 3 3 3 3 3 5 ( 0)ky kx = > 3 2 3 5 3 5 3 10 5 AB AB OA = = 2 210 6− ( 0)ky kx = > 12 x 12 8 3 2 3 2 故答案为（8， ）． 点评：本题考查了用待定系数法确定反比例的解析式；也考查了正弦的定义和勾股定理以及 求线段中点坐标． 10. （2011 浙江丽水，16，4 分）如图，将一块直角三角板 OAB 放在平面直角坐标系中，B （2，0），∠AOB=60°，点 A 在第一象限，过点 A 的双曲线为 ．在 x 轴上取一点 P，过 点 P 作直线 OA 的垂线 l，以直线 l 为对称轴，线段 OB 经轴对称变换后的像是 O´B´． （1）当点 O´与点 A 重合时，点 P 的坐标是　（4，0）　； （2）设 P（t，0），当 O´B´与双曲线有交点时，t 的取值范围是　4≤t≤ 或 ≤t≤﹣4　． 考点：反比例函数综合题；解二元一次方程组；根的判别式；解一元一次不等式；待定系数 法求一次函数解析式；待定系数法求反比例函数解析式；三角形内角和定理；含 30 度角的 直角三角形；勾股定理。 专题：计算题。 分析：（1）当点 O´与点 A 重合时，即点 O 与点 A 重合，进一步解直角三角形 AOB，利用 轴对称的现在解答即可； （2）求出∠MP′O=30°，得到 OM= t，OO′=t，过 O′作 O′N⊥X 轴于 N，∠OO′N=30°，求出 O′的坐标，同法可求 B′的坐标，设直线 O′B′的解析式是 y=kx+b，代入得得到方程组 ，求出方程组的解即可得到解析式 y=（ ）x﹣ t2+ t，求出反比例函数的解析式 y= ，代入上式整理得出方程（2 t﹣8 ）x2+（﹣ t2+6 t）x﹣4 =0，求出方程的判别式 b2﹣4ac≥0，求出不等式的解集即可． 解答：解：（1）当点 O´与点 A 重合时 ∵∠AOB=60°，过点 P 作直线 OA 的垂线 l，以直线 l 为对称轴，线段 OB 经轴对称变换后的 像是 O´B´． 3 2 ky x = 2 5 2 5− 1 2 3 1 2 2 23 2 3 2 t tk b tt k b  = + + − = + 3 2 32 t − 3 4 3 3 2 4 3 x 3 3 3 3 3 AP′=OP′， ∴△AOP′是等边三角形， ∵B（2，0）， ∴BO=BP′=2， ∴点 P 的坐标是（4，0）， 故答案为：（4，0）． （2）解：∵∠AOB=60°，∠P′MO=90°， ∴∠MP′O=30°， ∴OM= t，OO′=t， 过 O′作 O′N⊥X 轴于 N， ∠OO′N=30°， ∴ON= t，NO′= t， ∴O′（ t， t）， 同法可求 B′的坐标是（ ， t﹣2 ）， 设直线 O′B′的解析式是 y=kx+b，代入得； ， 解得： ， ∴y=（ ）x﹣ t2+ t， ∵∠ABO=90°，∠AOB=60°，OB=2， ∴OA=4，AB=2 ， 1 2 1 2 3 2 1 2 3 2 3 3 3 1 2 2 23 2 3 2 t tk b tt k b  = + + − = + 2 3 2 32 3 3 3 4 2 k t b t t  = −  = − + 3 ∴A（2，2 ），代入反比例函数的解析式得：k=4 ， ∴y= ，代入上式整理得：（2 t﹣8 ）x2+（﹣ t2+6 t）x﹣4 =0， b2﹣4ac= ﹣4（2 t﹣8 ）•（﹣4 ）≥0， 解得：t≤2 t≥﹣2 ， ∵当点 O´与点 A 重合时，点 P 的坐标是（4，0） ∴4≤t≤2 错误！未找到引用源。或﹣2 错误！未找到引用源。≤t≤4， 故答案为：4≤t≤2 错误！未找到引用源。或﹣2 错误！未找到引用源。≤t≤4． 点评：本题主要考查对用待定系数法求一次函数、反比例函数的解析式，勾股定理，解二元 一次方程组，解不等式，含 30 度角的直角三角形的性质，三角形的内角和定理，根的判别 式等知识点的理解和掌握，能综合运用这些性质进行计算是解此题的关键，此题是一个拔高 的题目，有一定的难度． 三、解答题 1. （2011 内蒙古呼和浩特，21，8）在同一直角坐标系中反比例函数 的图象与一次函 数 y=kx+b 的图象相交，且其中一个交点 A 的坐标为（-2，3），若一次函数的图象又与 x 轴 相交于点 B，且△AOB 的面积为 6（点 O 为坐标原点）．求一次函数与反比例函数的解析 式． 考点：反比例函数与一次函数的交点问题． 专题：综合题． 分析：将点 A（-2，3）代入 中得，得到 m=-2×3=-6，即得到反比例函数的解析式；由 △AOB 的面积为 6，求出 OB，得到 B 点坐标为（4，0）或（-4，0），然后分类讨论： 一次函数 y=kx+b 过（-2，3）和（4，0）或一次函数 y=kx+b 过（-2，3）和（-4，0），利用 待定系数法求出一次函数的解析式． 解答：解：将点 A（-2，3）代入 中得，m=-2×3=-6，∴m=-6，∴y=- ， 又∵△AOB 的面积为 6，∴ •OB•3=6，∴OB=4，∴B 点坐标为（4，0）或（-4，0）， ①当 B（4，0）时，∵点 A（-2，3）是两函数的交点，∴ ， 解得 k=- ，b=2，∴y=- x+2； ②当 B（-4，0）时， ∵点 A（-2，3）是两函数的交点，∴ ，解得 k= ，b=6，∴y= x+6． 3 3 4 3 x 3 3 3 3 3 2 2( 3 6 3)t− + 3 3 3 5 5 my x = my x = my x = 6 x 1 2 {4 0 2 3 k b k b + = − + = 1 2 1 2 {4 0 2 3 k b k b + = − + = 3 2 3 2 所以一次函数的解析式为 y=- x+2 或 y= x+6；反比例函数的解析式为 y=- ． 点评：本题考查了利用待定系数法求函数的解析式；也考查了分类讨论思想的运用以及 三角形的面积公式． 2. （2011 四川广安，24，8 分）如图 6 所示，直线 l1 的方程为 y＝－x＋l，直线 l2 的方程为 y＝x＋5，且两直线相交于点 P，过点 P 的双曲线 与直线 l1 的另一交点为 Q（3， M）． （1）求双曲线的解析式． （2）根据图象直接写出不等式 ＞－x＋l 的解集． 考点：反比例函数的解析式，函数图象的交点，一次函数与反比例函数的综合，利用图 象解不等式 专题：一次函数与反比例函数的综合 分析：（1）要确定双曲线 的解析式，关键是确定图象上点 P 的坐标，而点 P 是 直线 与 的交点，建立方程组即可求得交点坐标； （2）要求不等式 ＞－x＋l 的解集，表现在图象上就是确定当 在何范围内取值时， 双曲线 的图象在直线 的上方． 解答：（1）依题意： 解得： ，∴P（－2，3）． 把 P（－2，3）代入 ，得 ． ∴双曲线的解析式为：y＝ （2）－2＜x＜0 或 x>3． 点评：（1）确定反比例函数 的解析式，只需确定其图象上一点 ，则 ． ky x = k x ky x = 1y x= − + 5y x= + k x x ky x = 1y x= − + 1, 5. y x y x = − +  = + 2, 3. x y = −  = ky x = 3 , 62 k k= = −− 6 x − ky x = ( )0 0,x y 0 0k x y= 1 2 3 2 6 x （2）利用图象比较反比例函数的值与一次函数的值的大小时， 要充分利用数形结合思想进 行分析判断，要注意把反比例函数图象与一次函数图象的交点作为界点进行分析，还应注意 反比例函数中自变量 的性质． 3. （2011•南通）如图，直线 l 经过点 A(1，0)，且与双曲线 y＝ （x＞0）交于点 B(2， 1)，过点 P(p，p－1)（p＞1）作 x 轴的平行线分别交曲线 y＝ （x＞0）和 y＝－ （x ＜0）于 M，N 两点. （1）求 m 的值及直线 l 的解析式； （2）若点 P 在直线 y＝2 上，求证：△PMB∽△PNA； （3）是否存在实数 p，使得 S△AMN＝4S△APM？若存在，请求出所有满足条件的 p 的值； 若不存在，请说明理由. 考点：反比例函数综合题；待定系数法求一次函数解析式；相似三角形的判定与性质。 专题：计算题。 分析：（1）将点 B 的坐标代入即可得出 m 的值，设直线 l 的解析式为 y=kx+b，再把 点 A、B 的坐标代入，解方程组求得 k 和 b 即可得出直线 l 的解析式； （2）根据点 P 在直线 y=2 上，求出点 P 的坐标，再证明△PMB∽△PNA 即可； （3）先假设存在，利用 S△AMN=4S△AMP．求得 p 的值，看是否符合要求． 【解】（1）∵点 B(2，1)在双曲线 y＝ 上，∴ ，得 m＝2. 设直线 l 的解析式为 y＝kx＋b ∵直线 l 过 A(1，0)和 B(2，1)∴ ，解得 ∴直线 l 的解析式为 y＝x－1. (2) 证明：当 x＝p 时，y＝p－1，点 P(p，p－1)（p＞1） 在直线 l 上，如右图. ∵P(p，p－1)（p＞1）在直线 y＝2 上，∴p－1＝2，解得 p＝3∴P(3，2) ∵PN∥x 轴，∴P、M、N 的纵坐标都等于 2 把 y＝2 分别代入双曲线 y＝ 和 y＝ ， 解答：得 M(1，2)，N(-1，2) ∴ ，即 M 是 PN 的中点， 同理：B 是 PA 的中点，∴BM∥AN∴△PMB∽△PNA. 0x ≠ m x m x m x m x 1 2 m= 0 2 1 k b k b + =  + = 1 1 k b =  = − 2 x 2 x − 3 1 11 ( 1) PM MN −= =− − （3）由于 PN∥x 轴，P(p，p－1)（p＞1）， ∴M、N、P 的纵坐标都是 p－1（p＞1） 把 y＝p－1 分别代入双曲线 y＝ （x＞0）和 y＝－ （x＜0）， 得 M 的横坐标 x＝ 和 N 的横坐标 x＝－ （其中 p＞1） ∵S△AMN＝4S△APM 且 P、M、N 在同一直线上，∴ ，得 MN=4PM 即 ＝4 （见（3）两幅图）整理得：p2－p－3＝0 或 p2－p －1＝0 解得：p＝ 或 p＝ 由于 p＞1，∴负值舍去∴p＝ 或 经检验 p＝ 和 是原题的解，∴存在实数 p，使得 S△AMN＝4S△APM， p 的值为 或 . 点评：本题考查的知识点是反比例函数的综合题，以及用待定系数法求反比例函数和一次函 数的解析式，相似三角形的判定和性质 4. （2011•宁夏，24，8 分）在 Rt△ABC 中，∠C=90°，∠A=30°，BC=2．若将此直角三角形 的一条直角边 BC 或 AC 与 x 轴重合，使点 A 或点 B 刚好在反比例函数 （x＞0）的图 象上时，设△ABC 在第一象限部分的面积分别记做 S1、S2（如图 1、图 2 所示）D 是斜边与 y 轴的交点，通过计算比较 S1、S2 的大小． 2 x 2 x 2 1p − 2 1p − 4AMN APM S MN S PM ∆ ∆ = = 4 1p − 2 1p p − − 1 13 2 ± 1 5 2 ± 1 13 2 + 1 5 2 + 1 13 2 + 1 5 2 + 1 13 2 + 1 5 2 + xy 6= 考点：反比例函数综合题。 专题：计算题。 分析：根据反比例函数的性质，可以得到点 A 和点 B 的坐标，分别计算出 S1，S2 的值，然 后比较它们的大小． 解答：解：如图 1：∵∠C=90°，∠A=30°，BC=2， ∴AC=2 ， ∵点 A 在 上， ∴A（ ，2 ）， 即 OC= ， OB=2﹣ ， OD=2 ﹣3， ∴S1= （OD+AC）•OC， = （2 ﹣3+2 ）× ， =6﹣ ． 如图 2：BC=2，AC=2 ， B（3，2）， ∴AO=2 ﹣3， OD=2﹣ ， S2= （OD+BC）•OC， = （2﹣ +2）×3， 3 xy 6= 3 3 3 3 3 2 1 2 1 3 3 3 2 33 3 3 3 2 1 2 1 3 =6﹣ ． 所以 S1=S2． 点评：本题考查的是反比例函数的综合题，根据反比例函数的性质，结合图形计算面积． 5. （2011 山西，20，7 分）如图，在平面直角坐标系中，一次函数 y＝k x＋b 的图象分别交 x 轴、y 轴于 A、B 两点，与反比例函数 的图象交于 C、D 两点，DE⊥x 轴于点 E，已知 C 点的坐标是（6，－1），DE＝3． （1）求反比例函数与一次函数的解析式． （2）根据图象直接回答：当 x 为何值时，一次函数的值大于反比例函数的值？ 考点：一次函数，反比例函数 专题：一次函数，反比例函数 分析：（1）∵点 C（6，－1）在反比例函数 的图象上，代入，计算得 m＝－ 6． ∴反比例函数的解析式为 ．∵点 D 也在反比例函数 的图象上，且 DE＝ 3，∴代入得 ，计算得 x＝－2，∴点 D 的坐标为（－2，3），然后用待定系数法可得 一次函数的解析式为 ． ⑵用图像法得，当 x＜－2 或 0＜x＜6 时，一次函数的值大于反比例函数的值． 解答：（1）∵点 C（6，－1）在反比例函数 的图象上，所以 ， ∴m＝－6，∴反比例函数的解析式为 ， ∵点 D 在反比例函数 的图象上，且 DE＝3， ∴ ，∴x＝－2，∴点 D 的坐标为（－2，3）， ∵C、D 两点在直线 y＝k x＋b 上，所以 ， x my = my x = 6y x = − xy 6−= x 63 −= 1 22y x= − + x my = 1 6 m− = xy 6−= xy 6−= x 63 −=  =+− −=+ 32 16 bk bk 2 33 解得 ，所以一次函数的解析式为 ． （2）当 x＜－2 或 0 ＜x＜ 6 时，一次函数的值大于反比例函数的值． 点评：用待定系数法求反比例函数的解析式的条件是有一个已知点在此函数图像上； 用待 定系数法求一次函数的解析式的条件中有两个已知点在此函数图像上．用数形结合思想，直 接观察图象，就可以得到一次函数的值大于反比例函数的值的自变量 x 的取值范围，这是用 图像法解决问题的常规考题之一． 6.（2011 天津，20， 分）已知一次函数 y 1=x+b（b 为常数）的图象与反比例函数 （k 为常数，且 k≠0 ）的图象相交于点 P（3，1）． （I ）求这两个函数的解析式： （II）当 x＞3 时，试判断 y1 与 y2 的大小，并说明理由． 考点：反比例函数与一次函数的交点问题。 专题：代数综合题；待定系数法。 分析：（I）利用待定系数法，将 P（3，1）代入一次函数解析式与反比例函数解析式，即 可得到答案； （II）当 x=3 时，y1=y2=1，再利用函数的性质一次函数 y1 随 x 的增大而增大，反比例函数 y2 随 x 的增大而减小，可以判断出大小关系． 解答：解：（1）∵点 P（3，1）在一次函数 y1=x+b（b 为常数）的图象上， ∴1=3+b， 解得：b=﹣2， ∴一次函数解析式为：y1=x﹣2． ∵点 P（3，1）在反比例函数 （k 为常数，且 k≠0 ）的图象上， ∴k=3×1=3， ∴反比例函数解析式为： ， （II）y1＞y2．理由如下： 当 x=3 时，y1=y2=1， 又当 x=3 时，y1 随 x 的增大而增大，反比例函数 y2 随 x 的增大而减小， ∴当 x=3 时，y1＞y2． 点评：此题主要考查了待定系数法求函数解析式和函数的性质，凡是图象上的点，都能使函 数解析式左右相等． 7. （2011 重庆綦江，23，10 分）如图，已知 A （4，a），B （－2，－4）是一次函数 y＝kx    = −= 2 2 1 b k 22 1 +−= xy 2 ky x = 2 ky x = 2 3y x = ＋b 的图象和反比例函数 y＝－ 的图象的交点． （1）求反比例函数和一次函数的解祈式； （2）求△A0B 的面积． 考点：反比例函数与一次函数的交点问题。 专题：几何图形问题；数形结合。 分析：（1）A（4，a），B（－2，－4）两点在反比例函数 y＝－ 的图象上，则由 m＝xy， 得 4a＝（－2）×（－4）＝m，可求 a、m 的值，再将 A、B 两点坐标代入 y＝kx＋b 中求 k、 b 的值即可； （2）设直线 AB 交 y 轴于 C 点，由直线 AB 的解析式求 C 点坐标，根据 S△AOB＝S△AOC＋ S△BOC 求面积． 解答：解：（1）将 A（4，a），B（－2，－4）两点坐标代入 y＝－ 中， 得 4a＝（－2）×（－4）＝m， 解得 a＝2，m＝8， 将 A（4，a），B（－2，－4）代入 y＝kx＋b 中， 得 ，解得 ， ∴反比例函数解析式为 y＝ ，一次函数的解祈式为 y＝x－2； （2）设直线 AB 交 y 轴于 C 点， 由直线 AB 的解析式 y＝x－2 得 C（0，－2）， ∴S△AOB＝S△AOC＋S△BOC＝ ×2×4＋ ×2×2＝6． x m x m x m    −=+− =+ 42 24 bk bk    −= = 2 1 b k x 8 2 1 2 1 点评：本题主要考查了待定系数法求反比例函数与一次函数的解析式．运用数形结合的方法 求图形的面积，做此类题要根据图形的特点，将所求三角形的面积问题划分为两个三角形求 解． 8. （2011 重庆市，23，10 分）如图, 在平面直角坐标系中，一次函数 (k≠0)的图 象与反比例函数 (m≠0)的图象相交于 A、B 两点． 求：（1）根据图象写出 A、B 两点的坐标并分别求出反比例函数和一次函数的解析式； （2）根据图象写出：当 x 为何值时，一次 函数值大于反比例函数值. 考点：反比例函数与一次函数的交点问题． 分析：（1）根据题意，可得出 A、B 两点的坐标，再将 A、B 两点的坐标代入 y=kx+b （k≠0）与 ，即可得出解析式； （2）即求出一次函数图象在反比例函数图象的上方时，x 的取值范围即可． 答案：23.解：（1）由图象可知：点 A 的坐标为（2， ） 点 B 的坐标为（-1，-1） ∵反比例函数 (m≠0)的图像经过点（2， ） ∴ m=1 y kx b= + x my = A O x B y 1− 1− 2 1 2 23题图 1 2 x my = 1 2 ∴反比例函数的解析式为: ∵一次函数 y=kx+b(k≠0)的图象经过点（2， ）点 B（-1，-1） ∴ 解得：k= b=- ∴一次函数的解析式为 (2)由图象可知：当 x＞2 或 -1＜x＜0 时一次函数值大于反比例函数值 . 点评：本题考查了一次函数和反比例函数的交点问题，是基础知识要熟练掌握． 9.（2010 重庆，22，10 分）如图，在平面直角坐标系 x0y 中，一次函数 y=kx+b（k≠0）的图 象与反比例函数 （m≠0）的图象交于二、四象限内的 A、B 两点，与 x 轴交于 C 点， 点 B 的坐标为（6，n）．线段 OA=5，E 为 x 轴上一点，且 sin∠AOE= ． （1）求该反比例函数和一次函数的解析式； （2）求△AOC 的面积． 考点：反比例函数综合题 分析：（1）过点 A 作 AD⊥x 轴于 D 点，由 sin∠AOE= ，OA=5，根据正弦的定义可求出 AD，再根据勾股定理得到 DO，即得到 A 点坐标（﹣3，4），把 A（﹣3，4）代入 y= ， 确定反比例函数的解析式为 y=﹣ ；将 B（6，n）代入，确定点 B 点坐标，然后把 A 点和 B 点坐标代入 y=kx+b（k≠0），求出 k 和 b． （2）先令 y=0，求出 C 点坐标，得到 OC 的长，然后根据三角形的面积公式计算△AOC 的 面积即可． 解答：解：（1）过点 A 作 AD⊥x 轴于 D 点，如图， 1y x = 1 2 12 2 1 k b k b  + = − + = − 1 2 2 1 1 1 2 2y x= − my x = 4 5 A E O C B x y 22 题 图 4 5 m x 12 x A O x B y 1− 1− 2 1 2 23题图 ∵sin∠AOE= ，OA=5， ∴sin∠AOE= = = ， ∴AD=4， ∴DO= =3， 而点 A 在第二象限， ∴点 A 的坐标为（﹣3，4）， 将 A（﹣3，4）代入 y= ，得 m=﹣12， ∴反比例函数的解析式为 y=﹣ ； 将 B（6，n）代入 y=﹣ ，得 n=﹣2； 将 A（﹣3，4）和 B（6，﹣2）分别代入 y=kx+b（k≠0），得 ， 解得 ， ∴所求的一次函数的解析式为 y=﹣ x+2； （2）在 y=﹣ x+2 中，令 y=0， 即﹣ x+2=0， 解得 x=3， ∴C 点坐标为（0，3），即 OC=3， ∴S△AOC= •AD•OC= •4•3=6． 点评：本题考查了点的坐标的求法和点在图象上，点的横纵坐标满足图象的解析式；也考查 了正弦的定义、勾股定理以及三角形面积公式． 10. （2011 湖北潜江，21，8 分）如图，已知直线 AB 与 x 轴交于点 C，与双曲线 y＝ 交 4 5 AD OA 5 AD 4 5 2 25 4− m x 12 x 12 x 3 4 6 2 k b k b − + =  + = − ， ． 2 3 2 k b  = −  = ， ． 2 3 2 3 2 3 1 2 1 2 x k 于 A（3， ）、B（—5，a）两点．AD⊥x 轴于点 D，BE∥x 轴且与 y 轴交于点 E． （1）求点 B 的坐标及直线 AB 的解析式； （2）判断四边形 CBED 的形状，并说明理由． 考点：反比例函数综合题。 专题：计算题；几何图形问题。 分析：（1）根据反比例函数图象上点的坐标特征，将点 A 代入双曲线方程求得 k 值，即利 用待定系数法求得双曲线方程；然后将 B 点代入其中，从而求得 a 值；设直线 AB 的解析式 为 y＝mx＋n，将 A、B 两点的坐标代入，利用待定系数法解答； （2）由点 C、D 的坐标、已知条件“BE∥x 轴”及两点间的距离公式求得，CD＝5，BE＝5， 且 BE∥CD，从而可以证明四边形 CBED 是平行四边形；然后在 Rt△OED 中根据勾股定理求 得 ED＝5，所以 ED＝CD，从而证明四边形 CBED 是菱形． 解答：解：（1）∵双曲线 y＝ 过 A（3， ）， ∴k＝20． 把 B（—5，a）代入 y＝ ，得 a＝—4． ∴点 B 的坐标是（—5，—4）．（2 分） 设直线 AB 的解析式为 y＝mx＋n， 将 A（3， ）、B（—5，—4）代入，得 ，解得： ． ∴直线 AB 的解析式为：y＝ x＋ ；（4 分） （2）四边形 CBED 是菱形．理由如下：（5 分） 点 D 的坐标是（3，0），点 C 的坐标是（—2，0）． ∵BE∥x 轴， 3 20 x k 3 20 x 20 3 20    +−=− += nm nm 54 33 20      = = 3 8 3 4 n m 3 4 3 8 ∴点 E 的坐标是（0，—4）． 而 CD＝5，BE＝5，且 BE∥CD． ∴四边形 CBED 是平行四边形．（6 分） 在 Rt△OED 中，ED2＝OE2＋OD2， ∴ED＝ ＝5， ∴ED＝CD． ∴四边形 CBED 是菱形．（8 分） 点评：本题考查了反比例函数综合题．解答此题时，利用了反比例函数图象上点的坐标特 征． 11. （2011•贵港）如图所示，反比例函数 y= 的图象与一次函数 y=kx﹣3 的图象在第一象限 内相交于点 A （4，m）． （1）求 m 的值及一次函数的解析式； （2）若直线 x=2 与反比例和一次函数的图象分别交于点 B、C，求线段 BC 的长． 考点：反比例函数综合题。 专题：函数思想。 分析：（1）由已知先求出 m，得出点 A 的坐标，再把 A 的坐标代入一次函数 y=kx﹣3 求出 k 的值即可求出一次函数的解析式． （2）把 x=2 代入 y= 和 y=x﹣3，得出点 B 和点 C 的纵坐标，即可求出线段 BC 的长． 解答：解：（1）∵点 A （4，m）在反比例函数 y= 的图象上， ∴m= =1， ∴A （4，1）， 把 A （4，1）代入一次函数 y=kx﹣3，得 4k﹣3=1， ∴k=1， ∴一次函数的解析式为 y=x﹣3， 22 43 + （2）∵直线 x=2 与反比例和一次函数的图象分别交于点 B、C， ∴当 x=2 时，yB= =2， yC=2﹣3=﹣1， ∴线段 BC 的长为|yB﹣yC|=2﹣（﹣1）=3． 点评：此题考查的知识点是反比例函数综合应用，解决本题的关键是利用反比例函数求得关 键点点 A 的坐标，然后利用待定系数法即可求出函数的解析式． 12. （2011•柳州）如图，直线 y=kx+k（k≠0）与双曲线 y= 在第一象限内相交于点 M， 与 x 轴交于点 A． （1）求 m 的取值范围和点 A 的坐标； （2）若点 B 的坐标为（3，0），AM=5，S△ABM=8，求双曲线的函数表达式． 考点：反比例函数综合题。 专题：综合题。 分析：（1）根据反比例函数图象的性质，当比例系数大于 0 时，函数图象位于第一三象限， 列出不等式求解即可；令纵坐标 y 等于 0 求出 x 的值，也就可以得到点 A 的坐标； （2）过点 M 作 MC⊥AB 于 C，根据点 A、B 的坐标求出 AB 的长度，再根据 S△ABM=8 求 出 MC 的长度，然后在 Rt△ACM 中利用勾股定理求出 AC 的长度，从而得到 OC 的长度， 也就得到点 M 的坐标，然后代入反比例函数解析式求出 m 的值，解析式可得． 解答：解：（1）∵y= 在第一象限内， ∴m﹣5＞0， 解得 m＞5， ∵直线 y=kx+k 与 x 轴相交于点 A， ∴令 y=0， 则 kx+k=0， 即 k（x+1）=0， ∵k≠0， ∴x+1=0， 解得 x=﹣1， ∴点 A 的坐标（﹣1，0）； （2）过点 M 作 MC⊥AB 于 C， ∵点 A 的坐标（﹣1，0）点 B 的坐标为（3，0）， ∴AB=4，AO=1， S△ABM= ×AB×MC= ×4×MC=8， ∴MC=4， 又∵AM=5， ∴AC=3，OA=1， ∴OC=2， ∴点 M 的坐标（2，4）， 把 M（2，4）代入 y= 得 4= ， 解得 m=13， ∴y= ． 点评：本题考查了反比例函数图象的性质，一次函数图象的性质，以及勾股定理，待定系数 法求函数解析式，综合性较强，但难度不大，审清题意是解题的关键． 13. （2011•安顺）如图，已知反比例函数 的图象经过第二象限内的点 A（﹣1，m）， AB⊥x 轴于点 B，△AOB 的面积为 2．若直线 y=ax+b 经过点 A，并且经过反比例函数 的图象上另一点 C（n，一 2）． （1）求直线 y=ax+b 的解析式； （2）设直线 y=ax+b 与 x 轴交于点 M，求 AM 的长． 考点：反比例函数综合题。 专题：综合题。 分析：（1）根据点 A 的横坐标与△AOB 的面积求出 AB 的长度，从而得到点 A 的坐标，然 后利用待定系数法求出反比例函数解析式，再利用反比例函数解析式求出点 C 的坐标，根 据点 A 与点 C 的坐标利用待定系数法即可求出直线 y=ax+b 的解析式； （2）根据直线 y=ax+b 的解析式，取 y=0，求出对应的 x 的值，得到点 M 的坐标，然后求 出 BM 的长度，在△ABM 中利用勾股定理即可求出 AM 的长度． 解答：解：（1）∵点 A（﹣1，m）在第二象限内， ∴AB=m，OB=1， ∴S△ABO= AB•BO=2， 即： ×m×1=2， 解得 m=4， ∴A （﹣1，4）， ∵点 A （﹣1，4），在反比例函数 的图象上， ∴4= ， 解得 k=﹣4， ∵反比例函数为 y=﹣ ， 又∵反比例函数 y=﹣ 的图象经过 C（n，﹣2） ∴﹣2= ， 解得 n=2， ∴C （2，﹣2）， ∵直线 y=ax+b 过点 A （﹣1，4），C （2，﹣2） ∴ ， 解方程组得 ， ∴直线 y=ax+b 的解析式为 y=﹣2x+2； （2）当 y=0 时，即﹣2x+2=0， 解得 x=1， ∴点 M 的坐标是 M（1，0）， 在 Rt△ABM 中， ∵AB=4，BM=BO+OM=1+1=2， 由勾股定理得 AM= = = ． 点评：本题主要考查了反比例函数，待定系数法求函数解析式，勾股定理，综合性较强，但 只要细心分析题目难度不大． 14. （2011 黑龙江大庆，23，7 分）如图所示，制作一种产品的同时，需将原材料加热，设 该材料温度为 y℃，从加热开始计算的时间为 x 分钟．据了解，该材料在加热过程中温 度 y 与时间 x 成一次函数关系，已知该材料在加热前的温度为 l5℃，加热 5 分钟使材料 温度达到 60℃时停止加热，停止加热后，材料温度逐渐下降，这时温度 y 与时问 x 成 反比例函数关系． （1）分别求出该材料加热和停止加热过程中 y 与 x 的函数关系（要写出 x 的取值范）； （2）根据工艺要求，在材料温度不低于 30℃的这段时间内，需要对该材料进行特殊处理， 那么对该材料进行特殊处理所用的时间为多少分钟？ 考点：反比例函数的应用；一次函数的应用。 分析：（1）确定两个函数后，找到函数图象经过的点的坐标，用待定系数法求得函数 的解析式即可； （2）分别令两个函数的函数值为 30，解得两个 x 的值相减即可得到答案． 解答：解：（1）设加热过程中一次函数表达式为 y=kx+b 该函数图象经过点（0，15），（5，60） 即 ∴一次函数的表达式为 y=9x+15（0≤x≤5） 设加热停止后反比例函数表达式为 y= ，该函数图象经过点（5，60） 即 =60 解得：a=300 所以反比例函数表达式为 y= （x＞5） （2）由题意得： 解得 x1= 解得 x2=10 则 x2﹣x1=10﹣ = 所以对该材料进行特殊处理所用的时间为 分钟． 点评：本题考查了反比例函数的应用，解题的关键是从实际问题中整理出函数模型，利用函 数的知识解决实际问题． 15. 2011 山东菏泽，17，10 分）（1）已知一次函数 y=x+2 与反比例函数 ，其中一次函 数 y=x+2 的图象经过点 P（k，5）． ①试确定反比例函数的表达式； ②若点 Q 是上述一次函数与反比例函数图象在第三象限的交点，求点 Q 的坐标． 考点：反比例函数与一次函数的交点问题； 专题：数形结合；待定系数法．    = += 30 159 y xy    = = 30 300 y xy ky= x 分析：（1）①由一次函数 y=x+2 的图象经过点 P（k，5）可以得到 5=k+2，可以求出 k，也 就求出了反比例函数的表达式； ②由于点 Q 是上述一次函数与反比例函数图象在第三象限的交点，联立得方程组 ，解方程组即可求解； 解答：解：（1）①因一次函数 y=x+2 的图象经过点 P（k，5），所以得 5=k+2，解得 k=3， 所以反比例函数的表达式为 ； ②联立得方程组 ，解得 或 ，故第三象限的交点 Q 的坐标为 （﹣3，﹣1）． 点评：此题考查了待定系数法确定函数的解析式和函数图象的交点坐标与解析式的关系，有 一定的综合性，难度不大． 16. （2011•临沂，24，10 分）如图，一次函数 y=kx+b 与反比例函数 y= 的图象相较于 A （2，3），B（﹣3，n）两点． （1）求一次函数与反比例函数的解析式； （2）根据所给条件，请直接写出不等式 kx+b＞ 的解集； （3）过点 B 作 BC⊥x 轴，垂足为 C，求 S△ABC． 考点：反比例函数与一次函数的交点问题。 分析：（1）由一次函数 y=kx+b 与反比例函数 y= 的图象相较于 A（2，3），B（﹣3，n） 两点，首先求得反比例函数的解析式，则可求得 B 点的坐标，然后利用待定系数 法即可求得一次函数的解析式； 2 3 y x y x = + = 3y x = 2 3 y x y x = + = 1 3 x y =  = 3 1 x y = −  = − m x m x m x （2）根据图象，观察即可求得答案； （3）因为以 BC 为底，则 BC 边上的高为 3+2=5，所以利用三角形面积的求解方法即 可求得答案． 解答：解：（1）∵点 A（2，3）在 y= 的图象上， ∴m=6， ∴反比例函数的解析式为：y= ， ∴n= =﹣2， ∵A（2，3），B（﹣3，﹣2）两点在 y=kx+b 上， ∴ ， 解得： ， ∴一次函数的解析式为：y=x+1； （2）﹣3＜x＜0 或 x＞2； （3）以 BC 为底，则 BC 边上的高为 3+2=5， ∴S△ABC= ×2×5=5． 点评：此题考查了反比例函数与一次函数的交点问题．注意待定系数法的应用是解题的关 键． 17. （2011 泰安，26，10 分）如图，一次函数 y＝k1x＋b 的图象经过 A（0，－2），B（1， 0）两点，与反比例函数 的图象在第一象限内的交点为 M，若△OBM 的面积为 2． （1）求一次函数和反比例函数的表达式； （2）在 x 轴上是否存在点 P，使 AM⊥MP？若存在，求出点 P 的坐标；若不存在，说明理 m x 6 x 6 3− 3 2 2 3 k b k b = + − = − + 1 1 k b =  = 1 2 x ky 2= 由． 考点：反比例函数与一次函数的交点问题。 专题：探究型。 分析：（1）根据一次函数 y＝k1x＋b 的图象经过 A（0，－2），B（1，0）可得到关于 b．k1 的方程组，进而可得到一次函数的解析式，设 M（m，n）作 MD⊥x 轴于点 D，由△OBM 的 面积为 2 可求出 n 的值，将 M（m，4）代入 y＝2x－2 求出 m 的值，由 M（3，4）在双曲线 上即可求出 k2 的值，进而求出其反比例函数的解析式； （2）过点 M（3，4）作 MP⊥AM 交 x 轴于点 P，由 MD⊥BP 可求出∠PMD＝∠MBD＝ ∠ABO，再由锐角三角函数的定义可得出 OP 的值，进而可得出结论． 解答：（1）∵直线 y＝k1x＋b 过 A（0，－2），B（1，0）两点 ∴， ∴ ∴已知函数的表达式为 y＝2x－2．（3 分） ∴设 M（m，n）作 MD⊥x 轴于点 D ∵S△OBM＝2， ∴， ∴ ∴n＝4（5 分） ∴将 M（m，4）代入 y＝2x－2 得 4＝2m－2， ∴m＝3 ∵M（3，4）在双曲线 上， ∴， ∴k2＝12 x ky 2=    =+ −= 0 2 1 bk b    = −= 2 2 1k b 22 1 =⋅ MDOB 22 1 =n x ky 2= 34 2k= ∴反比例函数的表达式为 （2）过点 M（3，4）作 MP⊥AM 交 x 轴于点 P， ∵MD⊥BP， ∴∠PMD＝∠MBD＝∠ABO ∴tan∠PMD＝tan∠MBD＝tan∠ABO＝ ＝2（8 分） ∴在 Rt△PDM 中， ， ∴PD＝2MD＝8， ∴OP＝OD＋PD＝11 ∴在 x 轴上存在点 P，使 PM⊥AM，此时点 P 的坐标为（11，0）（10 分） 点评：本题考查的是反比例函数与一次函数的交点问题，涉及到的知识点为用待定系数法求 一次函数与反比例函数的解析式．锐角三角函数的定义，熟知以上知识是解答此题的关 键． 18. （2011 山东烟台，22，8 分） 如图，已知反比例函数 （k1＞0）与一次函数 相交于 A、B 两 点，AC⊥x 轴于点 C. 若△OAC 的面积为 1，且 tan∠AOC＝2 . （1）求出反比例函数与一次函数的解析式； （2）请直接写出 B 点的坐标，并指出当 x 为何值时，反比例函数 y1 的值大于一次函数 y2 的 值？ 考点：反比例函数与一次函数的交点问题。 xy 12= 1 2= OB OA 2= MD PD 1 1 ky x = 2 2 21( 0)y k x k= + ≠ 分析：（1）设 OC=m．根据已知条件得，AC=2，则得出 A 点的坐标，从而得出反比例 函数的解析式和一次函数的表达式； （2）易得出点 B 的坐标，反比例函数 y1 的图象在一次函数 y2 的图象的上方时，即 y1 大于 y2． 解答：（1）在 Rt△OAC 中，设 OC＝m. ∵tan∠AOC＝ ＝2，∴AC＝2×OC＝2m. ∵S△OAC＝ ×OC×AC＝ ×m×2m＝1，∴m2＝1. ∴m＝1（负值舍去）. ∴A 点的坐标为（1，2）. 把 A 点的坐标代入 中，得 k1＝2. ∴反比例函数的表达式为 . 把 A 点的坐标代入 中，得 k2＋1＝2，∴k2＝1. ∴一次函数的表达式 . （2）B 点的坐标为（－2，－1）. 当 0＜x＜1 和 x＜－2 时，y1＞y2. 点评：本题考查了一次函数和反比例函数的交点问题，以及用待定系数法求二次函数的解析 式，是基础知识要熟练掌握． 19. （2011•山西）如图，在平面直角坐标系中，一次函数 y=kx+b 的图象分别交 x 轴、y 轴 于 A、B 两点，与反比例函数 的图象交于 C、D 两点，DE⊥x 轴于点 E．已知 C 点的 坐标是（6，﹣1），DE=3． （1）求反比例函数与一次函数的解析式． （2）根据图象直接回答：当 x 为何值时，一次函数的值大于反比例函数的值？ AC OC 1 2 1 2 1 1 ky x = 1 2y x = 2 2 1y k x= + 2 1y x= + my x = 考点：反比例函数与一次函数的交点问题。 专题：计算题。 分析：（1）根据题意，可得出 A 、B 两点的坐标，再将 A、B 两点的坐标代入 y=kx+b （k≠0）与 ，即可得出解析式； （2）即求出一次函数图象在反比例函数图象的上方时，x 的取值范围即可． 解答：解：（1）点 C（6，﹣1）在反比例函数 的图象上， ∴m=﹣6， ∴反比例函数的解析式 y=﹣ ； ∵点 D 在反比例函数 y=﹣ 上，且 DE=3， ∴x=﹣2， ∴点 D 的坐标为（﹣2，3）． ∵CD 两点在直线 y=kx+b 上， ∴ ， 解得 ， ∴一次函数的解析式为 y=﹣ x+2． （2）当 x＜﹣2 或 0＜x＜6 时，一次函数的值大于反比例函数的值． 点评：本题考查了一次函数和反比例函数的交点问题，是基础知识要熟练掌握． 20.（2011 四川达州，18，6 分）给出下列命题： 命题 1：直线 y=x 与双曲线 有一个交点是（1，1）； 命题 2：直线 y=8x 与双曲线 有一个交点是（ ，4）； 命题 3：直线 y=27x 与双曲线 有一个交点是（ ，9）； my x = my x = 6 x 6 x 6 1 2 3 k b k b + = −  + = 1 2 2 k b  = −  = 1 2 1y x = 2y x = 1 2 3y x = 1 3 命题 4：直线 y=64x 与双曲线 有一个交点是（ ，16）； … （1）请你阅读、观察上面命题，猜想出命题 n（n 为正整数）； （2）请验证你猜想的命题 n 是真命题． 考点：反比例函数与一次函数的交点问题。 专题：规律型。 分析：（1）根据题意给的数据可得到命题 n：直线 y=n 3x 与双曲线 有一个交点是 （ ，n2）； （2）把（ ，n2）分别代入直线 y=n3x 和双曲线 中，即可判断命题 n 是真命题． 解答：解：（1）命题 n：直线 y=n3x 与双曲线 有一个交点是（ ，n2）； （2）验证如下： 将（ ，n2）代入直线 y=n3x 得：右边= ，左边=n2， ∴左边=右边， ∴点（ ，n2）在直线 y=n3x 上， 同理可证：点（ ，n2）在双曲线 上， ∴直线 y=n3x 与双曲线 有一个交点是（ ，n2）． 点评：本题考查了点在图象上，点的横纵坐标满足图象的解析式；也考查了探究规律的方法： 从特殊到一般． 21. （2011 四川广安，24，8 分）如图 6 所示，直线 l1 的方程为 y＝－x＋l，直线 l2 的方程 为 y＝x＋5，且两直线相交于点 P，过点 P 的双曲线 与直线 l 1 的另一交点为 Q （3，M）． （1）求双曲线的解析式． （2）根据图象直接写出不等式 ＞－x＋l 的解集． ky x = k x 4y x = 1 4 ny x = 1 n 1 n ny x = ny x = 1 n 1 n 3 21n nn × = 1 n 1 n ny x = ny x = 1 n 考点：反比例函数的解析式，函数图象的交点，一次函数与反比例函数的综合，利用图 象解不等式 专题：一次函数与反比例函数的综合 分析：（1）要确定双曲线 的解析式，关键是确定图象上点 P 的坐标，而点 P 是 直线 与 的交点，建立方程组即可求得交点坐标； （2）要求不等式 ＞－x＋l 的解集，表现在图象上就是确定当 在何范围内取值时， 双曲线 的图象在直线 的上方． 解答：（1）依题意： 解得： ，∴P（－2，3）． 把 P（－2，3）代入 ，得 ． ∴双曲线的解析式为：y＝ （2）－2＜x＜0 或 x>3． 点评：（1）确定反比例函数 的解析式，只需确定其图象上一点 ，则 ． （2）利用图象比较反比例函数的值与一次函数的值的大小时， 要充分利用数形结合思 想进行分析判断，要注意把反比例函数图象与一次函数图象的交点作为界点进行分析，还应 注意反比例函数中自变量 的性质． 22. （2011 四川泸州，24，7 分）如图，已知函数 y= (x＞0)的图象与一次函数 y=kx+b 的 图象交于点 A（1，m），B（n，2）两点． （1）求一次函数的解析式； （2）将一次函数 y=kx+b 的图象沿 x 轴负方向平移 a（a＞0）个单位长度得到新图象，求这 个新图象与函数 y= (x＞0)的图象只有一个交点 M 时 a 的值及交点 M 的坐标． ky x = 1y x= − + 5y x= + k x x ky x = 1y x= − + 1, 5. y x y x = − +  = + 2, 3. x y = −  = ky x = 3 , 62 k k= = −− 6 x − ky x = ( )0 0,x y 0 0k x y= 0x ≠ x 6 x 6 考点：反比例函数与一次函数的交点问题． 分析：（1）将点 A（1，m），B（n，2）代入反比例函数的解析式，求得 m、n 的值， 然后将其代入一次函数解析式，即用待定系数法求一次函数解析式； （2）根据题意，写出一次函数变化后的新的图象的解析式，然后根据根的判别式求得 a 值．最后将 a 值代入其中，求得 M 的坐标即可． 解答：解：（1）∵点 A（1，m），B（n，2）在反比例函数的图象上，∴ m=6，2 n =6， 解得， m=6，n=3；∴一次函数 y=kx+b 的图象交于点 A（1，6），B（3，2）两点． ∴ 6=k+b 2=3k+b，解得， k=－2，b=8， ∴一次函数的解析式是 y=－2x+8； （2）一次函数 y=kx+b 的图象沿 x 轴负方向平移 a（a＞0）个单位长度得到新图象的解析式 是：y=－2（x+a）+8．根据题意，得 y=－2(x-a)+8 y= ，∴x2+（a+4）x+3=0； ∴这个新图象与函数 y= (x＞0)的图象只有一个交点，∴△=（a+4）2-12=0，解得，a=-4±2 ； ①当 a=-4－2 时，解方程组，得:x=3 y=2 ，∴M（ 3，2 ）； ②当 a=－4+2 时，解方程组，得 x=－3 y=－2 ∴M（－3，－2 ）． 综上所述，a=-4±2 ，M（ 3，2 ）或 M（－3，－2 ）． 点评：本题主要考查了反比例函数与一次函数交点问题．用待定系数法确定函数的解析 式，是常用的一种解题方法．同学们要熟练掌握这种方法． 23. 如图，正比例函数 y1=k1x 与反比例函数 相交于 A、B 点．已知点 A 的坐标为 A （4，n），BD⊥x 轴于点 D，且 S△BDO=4．过点 A 的一次函数 y3=k3x+b 与反比例函数的图象 交于另一点 C，与 x 轴交于点 E（5，0）． （1）求正比例函数 y1、反比例函数 y2 和一次函数 y3 的解析式； （2）结合图象，求出当 k3x+b＞ ＞k1x 时 x 的取值范围． 【考点】反比例函数与一次函数的交点问题． 【分析】（1）首先根据△BOD 的面积求出反比例函数解析式；再利用反比例函数图象上的 点的特征求出 A 点坐标，由于正比例函数经过 A 点；再利用代定系数法求出正比例函数解 析式；一次函数 y3=k3x+b 过点 A（4，2），E（5，0），再次利用代定系数法求出一次函数 解析式； x 6 x 6 3 3 3 3 3 3 3 3 3 3 2 2 ky x = 2k x （2）点 C 是一次函数 y3=-2x+10 与反比例函数解析式 y2= 的交点，用方程-2x+10= 先求 出 C 的坐标，再求出 D 点坐标，最后结合图象可以看出答案． 【解答】解：（1）∵S△BDO=4．∴k2=2×4=8，∴反比例函数解析式；y2= ， ∵点 A（4，n）在反比例函数图象上， ∴4n=8，n=2，∴A 点坐标是（4，2）， ∵A 点（4，2）在正比例函数 y1=k1x 图象上，∴2=k1•4，k1= ， ∴正比例函数解析式是：y1= x， ∵一次函数 y3=k3x+b 过点 A（4，2），E（5，0）， ∴ ，解得： ， ∴一次函数解析式为：y3=-2x+10； （2）由-2x+10= 解得另一交点 C 的坐标是（1，8）， 点 A（4，2）和点 D 关于原点中心对称，∴D（-4，-2）， ∴由观察可得 x 的取值范围是：x＜-4，或 1＜x＜4． 【点评】此题主要考查了待定系数法求函数解析式和图象上点的坐标，并结合图象看不等式 的解，关键掌握凡是图象经过的点都能满足解析式，利用代入法即可求出解析式或点的坐 标． 24. （2011 四川攀枝花，20）如图，已知反比例函数 y= （m 是常数，m≠0），一次函数 y=ax+b（a、b 为常数，a≠0），其中一次函数与 x 轴，y 轴的交点分别是 A（﹣4，0），B （0，2）．（1）求一次函数的关系式； （2）反比例函数图象上有一点 P 满足：①PA⊥x 轴；②PO= （O 为坐标原点），求反比 例函数的关系式； （3）求点 P 关于原点的对称点 Q 的坐标，判断点 Q 是否在该反比例函数的图象上． 考点：反比例函数综合题。 专题：计算题。 分析：（1）用待定系数法求解函数解析式即可得出答案；（2）先求出 P 点的坐标，然后用 8 x 8 x 8 x 1 2 1 2 3 3 4 2 5 0 k b k b + =  + = 3 2 10 k b = −  = 8 x x m 17 待定系数法即可求出函数解析式；（3）先求出 P 关于原点对称的点 Q 的坐标，然后 代入反比例函数验证即可． 解答：解：（1）∵一次函数 y=ax+b 与 x 轴，y 轴的交点分别是 A（﹣4，0），B（0，2）， ∴﹣4a+b=0，b=2， ∴a= ， ∴一次函数的关系式为：y= x+2； （2）设 P（﹣4，n）， ∴ ，解得：n=±1， 由题意知 n=﹣1，n=1（舍去）， ∴把 P（﹣4，﹣1）代入反比例函数 y= ， ∴m=4， 反比例函数的关系式为：y= ； （3）∵P（﹣4，﹣1），∴关于原点的对称点 Q 的坐标为 Q（4，1），把 Q（4，1）代入 反比例函数关系式符合题意，∴Q 在该反比例函数的图象上． 点评：本题考查了反比例函数的综合题，难度适中，关键是掌握用待定系数法求解函数解析 式． 25.（2011 四川雅安，23,10 分）如图，过 y 轴上点 A 的一次函数与反比例函数相交于 B、D 两点，B（﹣2，3），BC⊥x 轴于 C，四边形 OABC 面积为 4． （1）求反比例函数和一次函数的解析式； （2）求点 D 的坐标； （3）当 x 在什么取值范围内，一次函数的值大于反比例函数的值．（直接写出结果） 考点：反比例函数与一次函数的交点问题。 专题：计算题。 分析：（1）先设出反比例函数和一次函数的解析式：y= 和 y=ax+b，把点 B 的坐标 代入反比例函数的解析式求出 k 即可； （2）两个解析式联立，求得点 D 的坐标即可； （3）利用函数图象求出分别得出使一次函数的值大于反比例函数的值的 x 的取值范围． 2 1 2 1 ( ) 174 22 =+− n x m x 4 k x 解答：解：（1）设反比例函数的解析式 y= 和一次函数的解析式 y=ax+b，图象经过 点 B， ∴k=﹣6， ∴反比例函数解析式为 y=﹣ ， 又四边形 OABC 面积为 4． ∴（OA+BC）OC=8， ∵BC=3，OC=2， ∴OA=1， ∴A（0，1） 将 A、B 两点代入 y=ax+b 有 解得 ∴一次函数的解析式为 y=﹣x+1， （2）联立组成方程组得 ， 解得 x=﹣2 或 3， ∴点 D（3，﹣2） （3）x＜﹣2 或 0＜x＜3． 点评：此题主要考查了待定系数法求反比例函数解析式以及待定系数法求一次函数解 析式，利用图象判定函数的大小关系是中学的难点同学们应重点掌握． 26. (2011 四川雅安 23，10 分)如图，过 轴上点 A 的一次函数与反比例函数相交于 B．D 两 点， ， 于 C，四边形 OABC 面积为 4。 （1）求反比例函数和一次函数的解析式； （2）求点 D 的坐标； （3）当 在什么取值范围内，一次函数的值大于反比例函数的值。（直接写出结果） k x 6 x 1 2 3 b a b = − + = 1 1 a b = −  = 6 1 y x y x  = −  = − + y )3,2(−B 轴xBC ⊥ x 考点：反比例函数与一次函数的交点问题。 专题：计算题。 分析：（1）先设出反比例函数和一次函数的解析式：y= 和 y=ax+b，把点 B 的坐标代入反 比例函数的解析式求出 k 即可； （2）两个解析式联立，求得点 D 的坐标即可； （3）利用函数图象求出分别得出使一次函数的值大于反比例函数的值的 x 的取值范围． 解答：（1）设反比例函数解析式为 y= ,将 代入得 3= k=-6 所以反比例函数解析式为 y=－ ; 设 A（0，a）,由 四边形 OABC 面积为 4 得 =4，解得 a=1 设一次函数的解析式 y=mx+b,将 ，A（0，1）代入得 解得 所以一次函数的解析式为 y=－x+1 （2）由 得 ∴y=－x+1 所以点 D 的坐 标为（3，-2） （3）x＜-2 或 0＜x＜3 点评：此题主要考查了待定系数法求反比例函数解析式以及待定系数法求一次函数解析式， 利用图象判定函数的大小关系是中学的难点同学们应重点掌握． 27. 如图函数 y1=k1x+b 的图象与函数 （x＞0）的图象交于 A、B 两点，与 y 轴交于 C 点．已知 A 点的坐标为（2，1），C 点坐标为（0，3）． （1）求函数 y1 的表达式和 B 点坐标； （2）观察图象，比较当 x＞0 时，y1 和 y2 的大小． 【考点】反比例函数与一次函数的交点问题． 【专题】综合题．． x k )3,2(−B 2− k x 6 2 )3(2 +a )3,2(−B 3 2 1 0 m b b = +  = + － 1 1 m b = −  = 6 1 y x y x  =  = − + － 1 1 x 2 y 3 =  = － 2 2 x 3 y -2 =  = 2ky x = 【分析】（1）把 A（2，1），C（0，3）代入 y1=k1x+b 可求出 k1 和 b；把 A（2，1）代入 （x＞0）求出 k2，然后把两个解析式联立起来解方程组即可求出 B 点坐标；（2）观察 函数图象，当 x＞0，两图象被 A，B 分成三段，然后分段判断大小以及对应的 x 的值． 【解答】解：（1）由题意，得 ，解得 ， ∴y1=-x+3 又∵A 点在函数 上， ∴ ，解得 k2=2，∴ ， 解方程组 ，得 ， 所以点 B 的坐标为（1，2） （2）当 0＜x＜1 或 x＞2 时，y1＜y2； 当 1＜x＜2 时，y1＞y2； 当 x=1 或 x=2 时，y1=y2． 【点评】本题考查了点在图象上，点的横纵坐标满足图象的解析式；也考查了两个函数的函 数值的大小比较． 28. （2011 北京，17，5 分）如图，在平面直角坐标系 xOy 中，一次函数 y=﹣2x 的图象与 反比例函数 y= 的图象的一个交点为 A（﹣1，n）． （1）求反比例函数 y= 的解析式； （2）若 P 是坐标轴上一点，且满足 PA=OA，直接写出点 P 的坐标． 考点：反比例函数与一次函数的交点问题。 专题：代数综合题。 分析：（1）把 A 的坐标代入函数解析式即可求得 k 的值，即可得到函数解析式； （2）以 A 为圆心，以 OA 为半径的圆与坐标轴的交点就是 P． 解答：解：（1）∵点 A（﹣1，n）在一次函数 y=﹣2x 的图象上． 2ky x = 12 1 3 k b b + =  = 1 1 3 k b = −  = 2 2 ky x = 21 2 k= 2 2y x = 3 2 y x y x = − + = 1 1 1 2 x y =  = 2 2 2 1 x y =  = x k x k ∴n=﹣2×（﹣1）=2 ∴点 A 的坐标为（﹣1，2） ∵点 A 在反比例函数的图象上． ∴k=﹣2 ∴反比例函数的解析式是 y=﹣ ． （2）点 P 的坐标为（﹣2，0）或（0，4）． 点评：本题主要考查了待定系数法求反比例函数的解析式，用待定系数法确定函数的解 析式，是常用的一种解题方法．同学们要熟练掌握这种方法． 29. （2010 福建泉州，23，9 分）如图，在方格纸中建立直角坐标系，已知一次函数 y1=﹣x+b 的图象与反比例函数 的图象相交于点 A（5，1）和 A1． （1）求这两个函数的关系式； （2）由反比例函数 的图象特征可知：点 A 和 A1 关于直线 y=x 对称．请你根据图象， 填写点 A1 的坐标及 y1＜y2 时 x 的取值范围． 考点反比例函数与一次函数的交点问题 分析（1）将点 A（5，1）分别代入一次函数 y1=﹣x+b 与反比例函数 中，可求 b、k 的值，确定两个函数解析式； （2）抛物线关于直线 y=x 轴对称，可证直线 y1=﹣x+6 与直线 y=x 互相垂直，根据轴对 称性可求点 A1 的坐标，再根据 y1 与 y2 的图象的位置关系，求 x 的取值范围． x 2 2 ky x = 2 ky x = 2 ky x = 解答解：（1）∵点 A（5，1）是一次函数 y1=﹣x+b 图象与反比例函数 图象的交 点， ∴﹣5+b=1， =1，解得 b=6，k=5， ∴y1=﹣x+6，y2= ； （2）由函数图象可知 A1（1，5）， 当 0＜x＜1 或 x＞5 时，y1＜y2． 点评本题考查了反比例函数与一次函数的交点问题．关键是利用待定系数法求两个函数解析 式，结合图象的位置，对称性求解． 30. （2011 福建厦门，22）已知一次函数 y=kx+b 与反比例函数 y= 的图象相交于点 A（﹣1， m）、B（﹣4，n）． （1）求一次函数的关系式； （2）在给定的直角坐标系中画出这两个函数的图象，并根据图象回答：当 x 为何值时，一 次函数的值大于反比例函数的值？ 考点：反比例函数与一次函数的交点问题。 专题：探究型。 分析：（1）先把 A、B 两点坐标代入反比例函数解析式即可求出 m、n 的值，进而可得出 A、B 两点的坐标，再把 A、B 两点的坐标代入一次函数的关系式即可求出 k、b 的值，进而 可得出其关系式； （2）利用描点法在坐标系内画出两函数的图象，再利用数形结合进行解答即可． 解答：解：（1）把 A 点坐标代入反比例函数解析式得，m= =﹣4； 把 B 点坐标代入反比例函数解析式得，n= =﹣1； 故 A（﹣1，﹣4）、B（﹣4，﹣1）， 代入一次函数 y=kx+b 得， ，解得 ， 故一次函数的关系式为：y=﹣x﹣5； 2 ky x = 5 k 5 x 4 x 4 1− 4 1− 4 1 4 k b k b − = − + − = − + 1 5 k b = −  = − （2）如图所示： ∵由函数图象可知，当 x＜﹣4 或﹣1＜x＜0 时，一次函数的图象在反比例函数图象的上方， ∴当 x＜﹣4 或﹣1＜x＜0 时，一次函数的值大于反比例函数的值． 点评：本题考查的是反比例函数与一次函数的交点问题、利用描点法画一次函数及反比例函 数的图象及用待定系数法求一次函数的解析式，熟知以上知识是解答此题的关键． 31. （2011 甘肃兰州，24，7 分）如图，一次函数 的图象与反比例函数 （x>0） 的图象交于点 P，PA⊥x 轴于点 A，PB⊥y 轴于点 B，一次函数的图象分别交 x 轴、y 轴于点 C、点 D，且 S△DBP=27， . （1）求点 D 的坐标； （2）求一次函数与反比例函数的表达式； （3）根据图象写出当 x 取何值时，一次函数的值小于反比例函数的值？ 考点：反比例函数与一次函数的交点问题. 分析：（1）本题需先根据题意一次函数与 y 轴的交点，从而得出 D 点的坐标． （2）本题需先根据在 Rt△COD 和 Rt△CAP 中， ，OD=3，再根据 S△DBP=27，从而 得出 BP 得长和 P 点的坐标，即可求出结果． （3）根据图形从而得出 x 的取值范围即可． 3y kx= + my x = 1 2 OC CA = x y A O PB C D 解答：解：（1）∵一次函数 y=kx+3 与 y 轴相交 ∴根据题意，得：D（0，3） （2）在 Rt△COD 和 Rt△CAP 中， ，OD=3 ∴AP=6，OB=6∴DB=9Rt△DBP 中，∴ ，∴BP=6，P（6，﹣6） 一次函数的解析式为： 反比例函数解析式为： . （3）根据图象可得：当 x＞6 时，一次函数的值小于反比例函数的值． 点评：本题主要考查了反比例函数和一次函数的交点问题，在解题时要注意知识的综合 运用与图形相结合是解题的关键． 32.（2011 浙江嘉兴，19，6 分）如图，已知直线 y=﹣2x 经过点 P（﹣2，a），点 P 关于 y 轴的对称点 P′在反比例函数 （k≠0）的图象上． （1）求 a 的值； （2）直接写出点 P′的坐标； （3）求反比例函数的解析式． 考点：待定系数法求反比例函数解析式；一次函数图象上点的坐标特征；关于 x 轴．y 轴对 称的点的坐标． 专题：计算题． 分析：（1）把（﹣2，a）代入 y=﹣2x 中即可求 a； （2）坐标系中任一点关于 y 轴对称的点的坐标，其中横坐标等于原来点横坐标的相反数， 纵坐标不变； （3）把 P′代入 中，求出 k，即可得出反比例函数的解析式． 解答：解： 272 DB BP× = 3 32y x= − + 36y x = − ky x = ky x = （1）把（﹣2，a）代入 y=﹣2x 中，得 a=﹣2×（﹣2）=4， ∴a=4； （2）∵P 点的坐标是（﹣2，4），∴点 P 关于 y 轴的对称点 P′的坐标是（2，4）； （3）把 P′（2，4）代入函数式 ，得 4= ，∴k=8，∴反比例函数的解析式是 y= ． 点评：本题考查了待定系数法球反比例函数解析式，一次函数图象上点的坐标特征，关于 x 轴．y 轴对称点的坐标．知道经过函数的某点一定在函数的图象上，坐标系中任一点关于 x 轴．y 轴的点的特征． 33. （2011 浙江舟山，19，6 分）如图，已知直线 y＝－2x 经过点 P（－2，a），点 P 关于 y 轴的对称点 P′在反比例函数 y＝ （k≠0）的图象上． （1）求 a 的值； （2）直接写出点 P′的坐标； （3）求反比例函数的解析式． 考点：待定系数法求反比例函数解析式；一次函数图象上点的坐标特征；关于 x 轴、y 轴对 称的点的坐标。 专题：计算题。 分析：（1）把（－2，a）代入 y＝－2x 中即可求 a； （2）坐标系中任一点关于 y 轴对称的点的坐标，其中横坐标等于原来点横坐标的相反数， 纵坐标不变； （3）把 P′代入 y＝ 中，求出 k，即可得出反比例函数的解析式． 解答：解：（1）把（－2，a）代入 y＝－2x 中，得 a＝－2×（－2）＝4， ∴a＝4； （2）∵P 点的坐标是（－2，4）， ky x = 2 k 8 x x k x k ∴点 P 关于 y 轴的对称点 P′的坐标是（2，4）； （3）把 P′（2，4）代入函数式 y＝ ，得 4＝ ， ∴k＝8， ∴反比例函数的解析式是 y＝ ． 点评：本题考查了待定系数法球反比例函数解析式，一次函数图象上点的坐标特征，关于 x 轴、y 轴对称点的坐标．知道经过函数的某点一定在函数的图象上，坐标系中任一点关于 x 轴、y 轴的点的特征． 34. （2011 湖北武汉，16，3 分）如图，□ABCD 的顶点 A．B 的坐标分别是 A（﹣1，0），B （0，﹣2），顶点 C．D 在双曲线 y= 上，边 AD 交 y 轴于点 E，且四边形 BCDE 的面积是 △ABE 面积的 5 倍，则 k=　12　． 考点：反比例函数综合题。 专题：综合题。 分析：分别过 C．D 作 x 轴的垂线，垂足为 F．G，过 C 点作 CH⊥DG，垂足为 H，根据 CD∥AB，CD=AB 可证△CDH≌△ABO，则 CH=AO=1，DH=OB=2，由此设 C（m+1，n），D （m，n+2），C．D 两点在双曲线 y= 上，则（m+1）n=m（n+2），解得 n=2m，设直线 AD 解析式为 y=ax+b，将 A．D 两点坐标代入求解析式，确定 E 点坐标，求 S△ABE，根据 S 四边 形 BCDE=5S△ABE，列方程求 m．n 的值，根据 k=（m+1）n 求解． 解答：解：如图，过 C．D 两点作 x 轴的垂线，垂足为 F．G，DG 交 BC 于 M 点，过 C 点 作 CH⊥DG，垂足为 H， ∵CD∥AB，CD=AB， ∴△CDH≌△ABO， ∴CH=AO=1，DH=OB=2，设 C（m+1，n），D（m，n+2）， 则（m+1）n=m（n+2）=k， 解得 n=2m， 设直线 AD 解析式为 y=ax+b，将 A．D 两点坐标代入得 x k 2 k x 8 k x k x ， 解得 ， ∴y=2x+2，E（0，2），BE=4， ∴S△ABE= ×BE×AO=2， ∵S 四边形 BCDE=5S△ABE， ∴S△ABE+S 四边形 BEDM=10， 即 2+4×m=10， 解得 m=2， ∴n=2m=4， ∴k=（m+1）n=3×4=12． 故答案为：12． 点评：本题考查了反比例函数的综合运用．关键是通过作辅助线，将图形分割，寻找全等三 角形，利用边的关系设双曲线上点的坐标，根据面积关系，列方程求解． 35. （2011 湖南衡阳，25，10 分）如图．已知 A、B 两点的坐标分别为 A（0，2 ），B （2，0）．直线 AB 与反比例函数 的图象交于点 C 和点 D（﹣1，a）． （1）求直线 AB 和反比例函数的解析式． （2）求∠ACO 的度数． （3）将△OBC 绕点 O 逆时针方向旋转 α 角（α 为锐角），得到△OB′C′，当 α 为多少时， OC′⊥AB，并求此时线段 AB’的长． 考点：反比例函数综合题。 0 2 2 a b ma b m − + =  + = + 2 2 a b =  = 1 2 3 my x = 专题：综合题。 分析：（1）设直线 AB 的解析式为：y=kx+b，把 A（0， ），B（2，0）分别代入，得 到 a，b 方程组，解出 a，b，得到直线 AB 的解析式；把 D 点坐标代入直线 AB 的解析式， 确定 D 点坐标，再代入反比例函数解析式确定 m 的值； （2）由由 得 ， ，求出 C 点坐标（3， ），利用勾 股定理计算出 OC 的长，得到 OA=OC；在 Rt△OAB 中，利用勾股定理计算 AB，得到 ∠OAB=30°，从而得到∠ACO 的度数； （3）由∠ACO=30°，要 OC′⊥AB，则∠COC′=90°﹣30°=60°，即 α=60°，得到∠BOB′=60°，而 ∠OBA=60°，得到△OBB′为等边三角形，于是有 B′在 AB 上，BB′=2，即可求出 AB′． 解答：（1）设直线 AB 的解析式为 y=kx+b，则有 ，解得 ， ∴直线 AB 的解析式为 ． 把点 D（-1，a）代入 得 a = ， ∴点 D（-1， ） 把点 D（-1， ）代入 中得 m=－ ， ∴反比例函数的解析式为： ． （2）由 得 ， ， ∴C 的坐标为（3， ）， 过 C 作 CE⊥x 轴于点 E，则 OE=3，CE= ，所以 OC=2 ， ∵A（0， ） ∴OA= OC= ， ∴∠ACO=∠OAB． 在 Rt△AOB 中，∵tan∠OAB= ， ∴∠OAB=300． ∴∠ACO=∠OAB=300． （3）设 OC′与 AB 相交于点 N，∵OC′⊥AB，∴∠ONC=900， 2 3 3 2 3 3 3 y x y x  = − + = − 1 1 1 3 3 x y = − = 2 2 3 3 x y = = − 3− 2 3 2 0 b k b  = + = 3 2 3 k b  = − = 3 2 3y x= − + 3 2 3y x= − + 3 3 3 3 3 3 my x = 3 3 3 3y x = − 3 2 3 3 3 y x y x  = − + = − 1 1 1 3 3 x y = − = 2 2 3 3 x y = = − 3− 3 3 2 3 2 3 3 3 OB OA = ∵∠ACO=300，∴∠COC′=600． 故当 a 为 60 度时，OC′⊥AB． 在 Rt△AOB 中，∵∠OAB=300，∴∠CBM=∠ABO=600． 在 Rt△BCE 中，∵CE= ，∠CBE=600，∴BC=2． ∵OB=2 ∴OB=BC ∴∠BOC=300， ∵∠AOB=900，∠BOB′=600，∴∠AOB′=300， 在△AO B′和△COB 中， ∴△AO B′≌△COB ∴AB′=BC=2． 点评：本题考查了利用待定系数法求图象的解析式．也考查了点在函数图象上，点的横纵坐 标满足函数图象的解析式和旋转的性质以及含 30 度的直角三角形三边的关系． 36. （2010 河南，20，9 分）如图，一次函数 y1=k1x+2 与反比例函数 的图象交于点 A（4，m）和 B（﹣8，﹣2），与 y 轴交于点 C． （1）k1= ，k2=　16　； （2）根据函数图象可知，当 y1＞y2 时，x 的取值范围是　﹣8＜x＜0 或 x＞4　； （3）过点 A 作 AD⊥x 轴于点 D，点 P 是反比例函数在第一象限的图象上一点．设直线 OP 与线段 AD 交于点 E，当 S 四边形 ODAC：S△ODE=3：1 时，求点 P 的坐标． 考点：反比例函数综合题 3 OA OC AOB COB OB OB =  ′∠ = ∠  ′ = 2 2 ky x = 1 2 分析：（1）本题须把 B 点的坐标分别代入一次函数 y1=k1x+2 与反比例函数 的解析 式即可求出 k2、k1 的值． （2）本题须先求出一次函数 y1=k1x+2 与反比例函数 的图象的交点坐标，即可求出 当 y1＞y2 时，x 的取值范围． （3）本题须先求出四边形 OADC 的面积，从而求出 DE 的长，然后得出点 E 的坐标，最后 求出直线 OP 的解析式即可得出点 P 的坐标． 解答：（1）∵一次函数 y1=k1x+2 与反比例函数 的图象交于点 A（4，m）和 B（﹣8， ﹣2）， ∴k2=（﹣8）×（﹣2）=16， ﹣2=﹣8k1+2 ∴k1= （2）∵一次函数 y 1=k1x+2 与反比例函数 的图象交于点 A（4，﹣4）和 B（﹣8， ﹣2）， ∴当 y1＞y2 时，x 的取值范围是﹣8＜x＜0 或 x＞4； （3）由（1）知， ． ∴m=4，点 C 的坐标是（0，2）点 A 的坐标是（4，4）． ∴CO=2，AD=OD=4． ∴ ． ∵S 梯形 ODAC：S△ODE=3：1， ∴ 即 OD•DE=4， ∴DE=2． ∴点 E 的坐标为（4，2）． 又点 E 在直线 OP 上， ∴直线 OP 的解析式是 ． ∴直线 OP 与 的图象在第一象限内的交点 P 的坐标为（ ）． 故答案为： ，16，﹣8＜x＜0 或 x＞4 点评：本题主要考查了反比例函数的综合问题，在解题时要综合应用反比例函数的图象和性 质以及求一次函数与反比例函数交点坐标是本题的关键． 2 2 ky x = 2 2 ky x = 2 2 ky x = 1 2 2 2 ky x = 1 2 1 1622y x y x = + =， 2 4 4 122 2ODAC CO AOS OD + +∴ = × = × =梯形 1 1 12 43 3ODE ODACS S∴ = × = × =△ 梯形 1 2 1 2y x= 2 16y x = 4 2 2 2， 1 2 37. （2011 广东肇庆，23， 分）如图．一次函数 y=x+b 的图象经过点 B（﹣1，0），且与 反比例函数 （k 为不等于 0 的常数）的图象在第一象限交于点 A（1，n）．求： （1）一次函数和反比例函数的解析式； （2）当 1≤x≤6 时，反比例函数 y 的取值范围． 考点：反比例函数与一次函数的交点问题。 分析：（1）根据题意首先把点 B（﹣1，0）代入一次函数 y=x+b 求出一次函数解析式， 又点 A（1，n）在一次函数 y=x+b 的图象上，再利用一次函数解析式求出点 A 的坐标，然 后利用代入系数法求出反比例函数解析式， （2）根据反比例函数的性质分别求出当 x=1，x=6 时的 y 值，即可得到答案． 解答：解：（1）把点 B（﹣1，0）代入一次函数 y=x+b 得： 0=﹣1+b， ∴b=1， ∴一次函数解析式为：y=x+1， ∵点 A（1，n）在一次函数 y=x+b 的图象上， ∴n=1+1， ∴n=2， ∴点 A 的坐标是（1，2）． ∵反比例函数 的图象过点 A（1，2）． ∴k=1×2=2， ∴反比例函数关系式是：y= ，； （2）反比例函数 y= ，当 x＞0 时，y 随 x 的增大而减少， 而当 x=1 时，y=2，当 x=6 时，y= ， ∴当 1≤x≤6 时，反比例函数 y 的值： ≤y≤2． 点评：此题主要考查了一次函数与反比例函数的交点问题，解题的关键是利用待定系数 法求出解析式，再再利用性质求反比例函数 y 的取值范围． 38.（2011 广西百色，24，分）直线 y=﹣x﹣2 与反比例函数 y= 的图象交于 A、B 两点，且 与 x、y 轴交于 C、D 两点，A 点的坐标为（﹣3，k+4）． ky x = ky x = 2 x 2 x 1 3 1 3 x k （1）求反比例函数的解析式； （2）把直线 AB 绕着点 M（﹣1，﹣1）顺时针旋转到 MN，使直线 MN⊥x 轴，且与反比例 函数的图象交于点 N，求旋转角大小及线段 MN 的长． 考点：反比例函数综合题． 专题：综合题． 分析：（1）把 A（﹣3，k+4）代入直线 y=﹣x﹣2 得，可得到 k 的值，即确定反比例函数的 解析式； （2）由 C．D 两点的坐标得到∠OCD=45°；当直线 MN⊥x 轴，即可得到∠CMN=45°，得到旋 转角的度数；把 x=﹣1 代入 y=﹣ 可确定 N 点坐标，易得 MN 的长． 解答：解：（1）将 A（﹣3，k+4）代入直线 y=﹣x﹣2 得，k+4=﹣（﹣3）﹣2，解得 k=﹣3， ∴点 A 坐标为（﹣3，1）， 所以反比例函数的解析式为 y=﹣ ； （2）如图， ∵C、D 两点的坐标为（﹣2，0）、（0，﹣2）， ∴在△OCD 中，∠OCD=45°； ∵直线 MN⊥x 轴， ∴∠CMN=45°， ∴旋转角为 45°． 把 x=﹣1 代入 y=﹣ 得，y=3， ∴N 的坐标为（﹣1，3）， ∴MN 的长度=3﹣（﹣1）=4． 点评：本题考查了点在反比例函数图象上，点的横纵坐标满足其解析式．也考查了等腰直角 x 3 x 3 x 3 三角形的性质以及旋转的性质． 39.（2011 广西来宾，23，10 分）已知反比例函数 的图像与一次函数 的 图像交于点 A（1，4）和 B（m, -2）. (1)求这两个函数的关系式. （2）观察图像，写出使得 ＞ 成立的自变量 x 的取值范围。 （3）如果点 C 与点 A 关于 x 轴对称，求△ABC 的面积。 考点：反比例函数与一次函数的交点问题。 专题：计算题。 分析：（1）先根据点 A 的坐标求出反比例函数的解析式为 ，再求出 B 的坐标是 （1，﹣2），利用待定系数法求一次函数的解析式； （2）在一次函数的解析式中，令 x=0，得出对应的 y2 的值，即得出直线 y2=﹣x﹣1 与 y 轴 交点 C 的坐标，从而求出△AOC 的面积； （3）当一次函数的值小于反比例函数的值时，直线在双曲线的下方，直接根据图象写出一 次函数的值小于反比例函数的值 x 的取值范围﹣2＜x＜0 或 x＞1． 【答案】解：（1）把 A（1，4）代入 得 1= ，则 k=4 ∴ 把 B（m, -2）代入 得 m=-2 ∴B（-2, -2） 1 ky x = 2y ax b= + 1y 2y 1 4y x = 1 ky x = 4 k 1 4y x = 1 4y x = 把 A（1，4），B（-2, -2）代入 得 ∴ ∴ （2）当 x＜-2 或 0＜x＜1 时， ＞ （3）解:由对称性知 C（1，-4） ∴AC=8 过 B 做 BD⊥AC 于点 D ∴ ×AC×BD= ×8×3=12 40. （2011 湖北潜江、天门、仙桃、江汉油田，21，8 分）如图，已知直线 AB 与 轴交于点 C，与双曲线 交于 A（3， ）、B（-5， ）两点.AD⊥ 轴于点 D，BE∥ 轴且 与 轴交于点 E. （1）求点 B 的坐标及直线 AB 的解析式； （2）判断四边形 CBED 的形状，并说明理由. 考点：反比例函数综合题． 分析：（1）根据反比例函数图象上点的坐标特征，将点 A 代入双曲线方程求得 k 值，即 2y ax b= + 4 2 2 a b a b + = − + = − 2 2 a b =  = 2 2 2y x= + 1y 2y 1 2ABCS =  1 2 x x ky = 3 20 a x x y 利用待定系数法求得双曲线方程；然后将 B 点代入其中，从而求得 a 值；设直线 AB 的解析 式为 y=mx+n，将 A、B 两点的坐标代入，利用待定系数法解答； （2）由点 C、D 的坐标、已知条件“BE∥x 轴”及两点间的距离公式求得，CD=5，BE=5，且 BE∥CD，从而可以证明四边形 CBED 是平行四边形；然后在 Rt△OED 中根据勾股定理求得 ED=5，所以 ED=CD，从而证明四边形 CBED 是菱形． 答案：21．解：（1）∵双曲线 过 A（3， ），∴ .把 B（-5， ）代入 , 得 . ∴点 B 的坐标是（-5，-4）. 设直线 AB 的解析式为 ， 将 A（3， ）、B（-5，-4）代入得， ， 解得： . ∴直线 AB 的解析式为： . （2）四边形 CBED 是菱形.理由如下: 点 D 的坐标是（3,0），点 C 的坐标是（-2,0）. ∵ BE∥ 轴， ∴点 E 的坐标是（0,-4）. 而 CD =5， BE=5， 且 BE∥CD. ∴四边形 CBED 是平行四边形. 在 Rt△OED 中，ED2＝OE2＋OD2， ∴ ED＝ ＝5，∴ED＝CD. ∴□CBED 是菱形. 点评：本题考查了反比例函数综合题．解答此题时，利用了反比例函数图象上点的坐标特 征． 41. （2011 梧州，20，6 分）已知 B（2，n）是正比例函数 y=2x 图象上的点． （1）求点 B 的坐标； （2）若某个反比例函数图象经过点 B，求这个反比例函数的解析式． 考点：反比例函数与一次函数的交点问题。 专题：待定系数法。 分析：（1）把 B（2，n）代入正比例函数 y=2x 即可求出 n 的值，进而可求出 B 点坐标； （2）把 B（2，n）代入反比例函数 求出 k 的值，即可求出这个反比例函数的解析 式． 解答：解：（1）把 B（2，n）代入 y=2x 得：n=2×2=4， x ky = 3 20 20=k a xy 20= 4−=a nmxy += 3 20    +−=− += nm nm 54 33 20 3 8,3 4 == nm 3 8 3 4 += xy x 22 43 + ∴B 点坐标为（2，4）； （2）设过 B 点的反比例函数解析式为 y= ， 把 B（2，4）代入有 4= ，k=8． ∴所求的反比例函数解析式为 y= ． 点评：本题考查的是正比例函数及反比例函数图形上点的坐标特点、用待定系数法求反比例 函数的解析式，难度适中． 42. （2011•安顺，23，9 分）如图，已知反比例函数 的图象经过第二象限内的点 A （﹣1，m），AB⊥x 轴于点 B，△AOB 的面积为 2．若直线 y=ax+b 经过点 A，并且经过反比 例函数 的图象上另一点 C（n，一 2）． （1）求直线 y=ax+b 的解析式； （2）设直线 y=ax+b 与 x 轴交于点 M，求 AM 的长． 考点：反比例函数综合题。 专题：综合题。 分析：（1）根据点 A 的横坐标与△AOB 的面积求出 AB 的长度，从而得到点 A 的坐标， 然后利用待定系数法求出反比例函数解析式，再利用反比例函数解析式求出点 C 的坐标， 根据点 A 与点 C 的坐标利用待定系数法即可求出直线 y=ax+b 的解析式； （2）根据直线 y=ax+b 的解析式，取 y=0，求出对应的 x 的值，得到点 M 的坐标，然后求 出 BM 的长度，在△ABM 中利用勾股定理即可求出 AM 的长度． 解答：解：（1）∵点 A（﹣1，m）在第二象限内， ∴AB=m，OB=1， ∴S△ABO= AB•BO=2， x ky = x ky = 2 1 即： ×m×1=2， 解得 m=4， ∴A （﹣1，4）， ∵点 A （﹣1，4），在反比例函数 的图象上， ∴4= ， 解得 k=﹣4， ∵反比例函数为 y=﹣ ， 又∵反比例函数 y=﹣ 的图象经过 C（n，﹣2） ∴﹣2= ， 解得 n=2， ∴C （2，﹣2）， ∵直线 y=ax+b 过点 A （﹣1，4），C （2，﹣2） ∴ ， 解方程组得 ， ∴直线 y=ax+b 的解析式为 y=﹣2x+2； （2）当 y=0 时，即﹣2x+2=0， 解得 x=1， ∴点 M 的坐标是 M（1，0）， 在 Rt△ABM 中， ∵AB=4，BM=BO+OM=1+1=2， 由勾股定理得 AM= ． 点评：本题主要考查了反比例函数，待定系数法求函数解析式，勾股定理，综合性较强， 但只要细心分析题目难度不大． 43. 如图，一次函数图象与 x 轴相交于点 B，与反比例函数图象相交于点 A（1，-6）；△AOB 的面积为 6．求一次函数和反比例函数的解析式． 2 1 x ky = 1− k x 4 x 4 n 4−    +=− +−= ba ba 22 4    = −= 2 2 b a 5224 2222 =+=+ BMAB 【考点】反比例函数与一次函数的交点问题． 【分析】根据待定系数法就可以求出函数的解析式；再利用△BOA 的面积就是求 B 点的坐 标，然后再利用待定系数法求出一次函数解析式． 【解答】解：∵点 A（1，-6）在反比例函数图象上 ∴k=1×（-6）=-6，即反比例函数关系式为 ， ∵△AOB 的面积为 6．∴ ×OB×6=6，∴OB=2， ∴B（-2，0）， 设一次函数解析式为：y=kx+b，∵图象经过 A（1，-6），B（-2，0）， ∴ ，解得： ，∴一次函数解析式为：y=-2x-4， 【点评】此题主要考查了待定系数法求一次函数解析式与反比例函数解析式，关键把握住凡 是图象经过的点都能满足解析式． 44.（2011 湖南湘潭市，23，8 分）如图，已知一次函数 y=kx+b（k≠0）的图象与 x 轴，y 轴 分别交于 A（1，0）、B（0，-1）两点，且又与反比例函数 的图象在第一象 限交于 C 点，C 点的横坐标为 2． （1）求一次函数的解析式； （2）求 C 点坐标及反比例函数的解析式． 考点：反比例函数与一次函数的交点问题． 专题：计算题． 分析：（1）将 A（1，0）、B（0，-1）两点，代入 y=kx+b，求得 k，b，即可得出一次函 数的解析式； （2）将 x=2 代入一次函数的解析式，求得点 C 的纵坐标，再代入 y= ，求得 m，即可得 出反比例函数的解析式． 解答：解：（1）∵一次函数 y=kx+b（k≠0）的图象与 x 轴，y 轴分别交于 A（1，0）、B （0，-1）两点， 6y x = − 1 2 6 2 0 k b k b + = − − + = 2 4 k b = −  = − ( 0)my mx = ≠ ∴ ， 解得 k=1，b=-1， ∴一次函数的解析式为 y=x-1； （2）∵C 点的横坐标为 2， ∴y=2-1=1； 则 C（2，1）， ∴m=2， ∴反比例函数的解析式为 y= ． 点评：本题考查了一次函数和反比例函数的交点问题，以及用待定系数法求一次函数和反比 例的解析式． 45.（2011 吉林长春，19，6 分）如图，平面直角坐标系中，直线 与 x 轴交于点 A，与双曲线 在第一象限内交于点 B，BC 丄 x 轴于点 C，OC=2AO．求双曲线的解析 式． 考点：反比例函数综合题． 专题：综合题． 分析：先利用一次函数与图象的交点，再利用 OC=2AO 求得 C 点的坐标，然后代入一次函 数求得点 B 的坐标，进一步求得反比例函数的解析式即可． 解答：解：由直线 与 x 轴交于点 A 的坐标为（﹣1，0），∴OA=1．又∵OC=2OA， ∴OC=2， ∴点 B 的横坐标为 2，代入直线 ，得 y= ，∴B（2， ）．∵点 B 在双曲线上， ∴k=xy=2× =3，∴双曲线的解析式为 y= ． 点评：本题考查了反比例函数的综合知识，解题的关键是根据一次函数求出反比例函数与直 线的交点坐标． 46.（2011 巴彦淖尔，20，9 分）如图，点 D 双曲线上，AD 垂直 x 轴，垂足为 A，点 C 在 AD 0 1 k b b + =  = − 2 x 1 1 2 2y x= + ky x = 1 1 2 2y x= + 1 1 2 2y x= + 3 2 3 2 3 2 3 x 上，CB 平行于 x 轴交曲线于点 B，直线 AB 与 y 轴交于点 F，已知 AC：AD=1：3，点 C 的 坐标为（2，2）． （1）求该双曲线的解析式； （2）求△OFA 的面积． 考点：反比例函数综合题。 专题：反比例函数。 分析：（1）由点 C 的坐标为（2，2）得 AC=2，而 AC：AD=1：3，得到 AD=6，则 D 点坐 标为（2，6），然后利用待定系数法确定双曲线的解析式； （2）已知 A（2，0）和 B（6，2），利用待定系数法确定直线 AB 的解析式，得到 F 点的坐 标，然后利用三角形的面积公式计算即可. 解答 ：解：（1）∵点 C 的坐标为（2，2），AD 垂直 x 轴， ∴AC=2， 又∵AC：AD=1：3， ∴AD=6， ∴D 点坐标为（2，6）， 设双曲线的解析式为 y= ， 把 D（2，6）代入 y= 得，k=2×6=12， 所以双曲线解析式为 y= ； （3）设直线 AB 的解析式为 y=kx+b， 把 A（2，0）和 B（6，2）代入 y=kx+b 得，2k+b=0，6k+b=2，解得 k= ，b=﹣1， ∴线 AB 的解析式为 y= x﹣1， 令 x=0，得 y=﹣1， ∴F 点的坐标为（0，﹣1）， ∴S△OFC= ×OA×OF= ×2×1=1 点评：本题考查了利用待定系数法确定反比例函数和一次函数函数解析式的方法：把求解析 式的问题转化为解方程或方程组．也考查了坐标与线段之间的关系以及三角形面积公式． 47. （2011 四川省宜宾市，21，7 分）如图，一次函数的图象与反比例函数 y1= – 3 x ( x<0） 的图象相交于 A 点，与 y 轴、x 轴分别相交于 B、C 两点，且 C（2，0).当 x<–1 时，一次函 数值大于反比例函数的值，当 x>–1 时，一次函数值小于反比例函数值. (1) 求一次函数的解析式； (2) 设函数 y2= a x (x>0)的图象与 y1= – 3 x (x<0)的图象关于 y 轴对称.在 y2= a x (x>0)的图象上 取一点 P（P 点的横坐标大于 2)，过 P 作 PQ⊥x 轴，垂足是 Q，若四边形 BCQP 的面积 等于 2，求 P 点的坐标. 考点：反比例函数综合题． 分析：（1）根据 x＜-1 时，一次函数值大于反比例函数值，当 x＞-1 时候，一次函数值小 于反比例函数值得到点 A 的坐标，利用待定系数法求函数的解析式即可； （2）求得 B 点的坐标后设出 P 点的坐标，利用告诉的四边形的面积得到函数关系式求得点 P 的坐标即可． 答案：解：（1）∵x< –1 时，一次函数值大于反比例函数值，当 x>–1 时，一次函数值小于 反比例函数值. ∴A 点的横坐标是–1，∴A（–1，3） 设一次函数解析式为 y= kx+b，因直线过 A、C 则{–k + b = 3 2k + b = 0 ，解之得：{k = –1 b = 1 ， ∴一次函数解析式为 y= –x+2 （2）∵y2 = a x (x>0)的图象与 y1= – 3 x (x<0)的图象 y 轴对称， Q P O C B A y2y1 y x (21 题图) ∴y2 = 3 x (x>0) ∵B 点是直线 y= –x+2 与 y 轴的交点，∴B (0，2) 设 P（n，3 n )，n>2 S 四边形 BCQP –S△BOC =2 ∴1 2( 2+ 3 n )n– 1 2 ×2×2 = 2，n = 5 2， ∴P（5 2，6 5） 点评：此题主要考查反比例函数的性质，注意通过解方程组求出交点坐标．同时要注意运用 数形结合的思想． 48. 如图函数 y1=k1x+b 的图象与函数 （x＞0）的图象交于 A、B 两点，与 y 轴交于 C 点．已知 A 点的坐标为（2，1），C 点坐标为（0，3）． （1）求函数 y1 的表达式和 B 点坐标； （2）观察图象，比较当 x＞0 时，y1 和 y2 的大小． 【考点】反比例函数与一次函数的交点问题． 【专题】综合题．． 【分析】（1）把 A（2，1），C（0，3）代入 y1=k1x+b 可求出 k1 和 b；把 A（2，1）代入 （x＞0）求出 k2，然后把两个解析式联立起来解方程组即可求出 B 点坐标；（2）观察函数 图象，当 x＞0，两图象被 A，B 分成三段，然后分段判断大小以及对应的 x 的值． 【解答】解：（1）由题意，得 ，解得 ， ∴y1=-x+3 又∵A 点在函数 上， ∴ ，解得 k2=2，∴ ， 解方程组 ，得 ， 所以点 B 的坐标为（1，2） （2）当 0＜x＜1 或 x＞2 时，y1＜y2； 当 1＜x＜2 时，y1＞y2； 当 x=1 或 x=2 时，y1=y2． 【点评】本题考查了点在图象上，点的横纵坐标满足图象的解析式；也考查了两个函数的函 数值的大小比较． 49. （2011 浙江义乌，22，10 分）如图，在直角坐标系中，O 为坐标原点．已知反比例函 2ky x = 2ky x = 12 1 3 k b b + =  = 1 1 3 k b = −  = 2 2 ky x = 21 2 k= 2 2y x = 3 2 y x y x = − + = 1 1 1 2 x y =  = 2 2 2 1 x y =  = 数 y＝ （k＞0）的图象经过点 A（2，m），过点 A 作 AB⊥x 轴于点 B，且△AOB 的面积为 ． （1）求 k 和 m 的值； （2）点 C（x，y）在反比例函数 y＝ 的图象上，求当 1≤x≤3 时函数值 y 的取值范围； （3）过原点 O 的直线 l 与反比例函数 y＝ 的图象交于 P、Q 两点，试根据图象直接写出 线段 PQ 长度的最小值． 考点：反比例函数综合题。 专题：综合题。 分析：（1）根据三角形的面积公式先得到 m 的值，然后把点 A 的坐标代入 y＝ ，可求出 k 的值； （2）P，Q 关于原点对称，则 PQ＝2OP，设 P（a， ），根据勾股定理得到 OP= ，从而得到 OP 最小值为 ，于是可得到线段 PQ 长度的最 小值． 解答：解：（1）∵A（2，m）， ∴OB＝2，AB＝m， ∴S△AOB＝ •OB•AB＝ ×2×m＝ ， ∴m＝ ； ∴点 A 的坐标为（2， ）， 把 A（2， ）代入 y＝ ，得 ＝ ∴k＝1； （2）∵当 x＝1 时，y＝1；当 x＝3 时，y＝ ， 又∵反比例函数 y＝ ，在 x＞0 时，y 随 x 的增大而减小， x k 2 1 x k x k x k a 1 2)1()1( 222 +−=+ aaaa 2 2 1 2 1 2 1 2 1 2 1 2 1 x k 2 1 2 k 3 1 x 1 ∴当 1≤x≤3 时，y 的取值范围为 ≤y≤1； （3）由图象可得，线段 PQ 长度的最小值为 2 ． 点评：本题考查了点在图象上，点的横纵坐标满足图象的解析式；也考查了三角形的面积公 式以及代数式的变形能力． 50. （2011 四川眉山，12，3 分）如图，直线 y=﹣x+b（b＞0）与双曲线 y= （x＞0）交 于 A、B 两点，连接 OA、OB，AM⊥y 轴于 M，BN⊥x 轴于 N；有以下结论： ①OA=OB，②△AOM≌△BON，③若∠AOB=45°，则 S△AOB=k， ④当 AB= 时，ON﹣BN=1；其中结论正确的个数为（　　） A．1 B．2 C．3 D．4 考点：反比例函数综合题。 专题：计算题。 分析：①②设 A（x 1，y1），B（x 2，y2），联立 y=﹣x+b 与 y= ，得 x2﹣bx+k=0，则 x1•x2=k，又 x1•y1=k，比较可知 x2=y1，同理可得 x1=y2，即 ON=OM，AM=BN，可证结论； ③ 作 OH⊥AB ， 垂 足 为 H ， 根 据 对 称 性 可 证 △OAM≌△OAH≌△OBH≌△OBN ， 可 证 S△AOB=k； ④延长 MA，NB 交于 G 点，可证△ABG 为等腰直角三角形，当 AB= 时，GA=GB=1， 则 ON﹣BN=GN﹣BN=GB=1； 解答：解：设 A（x1，y1），B（x2，y2），代入 y= 中，得 x1•y1=x2•y2=k， 联立 ，得 x2﹣bx+k=0， 则 x1•x2=k，又 x1•y1=k， ∴x2=y1， 同理可得 x1=y2， ∴ON=OM，AM=BN， ∴①OA=OB，②△AOM≌△BON，正确； 3 1 2 x k 2 x k 2 x k    = +−= x ky bxy ③作 OH⊥AB，垂足为 H， ∵OA=OB，∠AOB=45°， ∴△OAM≌△OAH≌△OBH≌△OBN， ∴S△AOB=S△AOH+S△BOH=S△AOM+S△BON= k+ k=k，正确； ④延长 MA，NB 交于 G 点， ∵NG=OM=ON=MG，BN=AM， ∴GB=GA， ∴△ABG 为等腰直角三角形， 当 AB= 时，GA=GB=1， ∴ON﹣BN=GN﹣BN=GB=1，正确． 正确的结论有 4 个． 故选 D． 点评：本题考查了反比例函数的综合运用．关键是明确反比例函数图象上点的坐标特点，反 比例函数图象的对称性．. 51. （2011，四川乐山，,10,3 分）如图，直线 y=6﹣x 交 x 轴、y 轴于 A、B 两点，P 是反比 例函数 图象上位于直线下方的一点，过点 P 作 x 轴的垂线，垂足为点 M，交 AB 于点 E，过点 P 作 y 轴的垂线，垂足为点 N，交 AB 于点 F．则 AF•BE=（　　） 2 1 2 1 2 4 ( 0)y xx = 〉 A.8 B.6 C.4 D. 考点：反比例函数综合题。 专题：代数综合题；数形结合。 分析：首先作辅助线：过点 E 作 EC⊥OB 于 C，过点 F 作 FD⊥OA 于 D，然后由直线 y=6﹣x 交 x 轴、y 轴于 A、B 两点，求得点 A 与 B 的坐标，则可得 OA=OB，即可得 △AOB，△BCE，△ADF 是等腰直角三角形，则可得 AF•BE= CE• DF=2CE•DF，又由 四边形 CEPN 与 MDFP 是矩形，可得 CE=PN，DF=PM，根据反比例函数的性质即可求得答 案． 解答：解：过点 E 作 EC⊥OB 于 C，过点 F 作 FD⊥OA 于 D， ∵直线 y=6﹣x 交 x 轴、y 轴于 A、B 两点， ∴A（6，0），B（0，6）， ∴OA=OB， ∴∠ABO=∠BAO=45°， ∴BC=CE，AD=DF， ∵PM⊥OA，PN⊥OB， ∴四边形 CEPN 与 MDFP 是矩形， ∴CE=PN，DF=PM， ∵P 是反比例函数 图象上的一点， ∴PN•PM=4， ∴CE•DF=4， 在 Rt△BCE 中，BE= ， 在 Rt△ADE 中，AF= ， ∴AF•BE= CE• DF=2CE•DF=8． 6 2 2 2 4 ( 0)y xx = 〉 2sin 45 CE CE=° 2sin 45 DF DF=° 2 2 故选 A． 点评：此题考查了反比例函数的性质，以及矩形、等腰直角三角形的性质．解题的关键是注 意数形结合与转化思想的应用． 52. （2011 年四川省绵阳市，21，12 分）右图中曲线是反比例函数 x= 的图象的一 支． （1）这个反比例函数图象的另一支位于哪个象限？常数 n 的取值范围是什么？ （2）若一次函数 x= 的图象与反比例函数的图象交于点 A，与 x 轴交于点 B， △AOB 的面积为 2，求 n 的值． 考点：反比例函数综合题． 分析：（1）根据反比例函数的性质可求得反比例函数的图象分布在第二、第四象限，所以 n+7 ＜0 即可求解； （2）图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积 S= |k|，可利用△AOB 的面积求出 n 值． 解答：解：（1）这个反比例函数图象的另一支位于第四象限． 由 n+7＜0， 解得 n＜-7， 即常数 n 的取值范围是 n＜-7； （2）在 中令 y=0，得 x=2， 即 OB=2． 过 A 作 x 轴的垂线，垂足为 C，如图． 7ny x += 2 4 3 3y x= − + 1 2 2 4 3 3y x= − + ∵S△AOB=2，即 OB•AC=2， ∴ ×2×AC=2，解得 AC=2，即 A 点的纵坐标为 2． 把 y=2 代入 中，得 x=-1，即 A（-1，2）． 所以 ， 解得 n=-9． 点评：本题主要考查了反比例函数的性质和反比例函数 中 k 的几何意义．图象上的 点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积 S 的关系即 S= |k|． 53. （2011 成都，19，10 分）如图，已知反比例函数 （ ）的图象经过点（ ， 8），直线 y＝－x＋b 经过该反比例函数图象上的点 Q（4，m）． （1）求上述反比例函数和直线的函数表达式； （2）设该直线与 x 轴，y 轴分别相交于 A，B 两点，与反比例函数图象的另一个交点为 P， 连接 OP、OQ，求△OPQ 的面积． 考点：反比例函数综合题。 专题：综合题。 分析：（1）把点（ ，8）代入反比例函数 （ ），确定反比例函数的解析式为 y ＝ ；再把点 Q（4，m）代入反比例函数的解析式得到 Q 的坐标，然后把 Q 的坐标代入直 线 y＝－x＋b，即可确定 b 的值； （2）把反比例函数和直线的解析式联立起来，解方程组得到 P 点坐标；对于 y＝－x＋5， 1 2 1 2 2 4 3 3y x= − + 72 1 n += − 1 2 x ky = 0≠k 2 1 2 1 x ky = 0≠k x 4 令 y＝0，求出 A 点坐标，然后根据 S△OPQ＝S△AOB－S△OBP－S△OAQ 进行计算即可． 解答：解：（1）把点（ ，8）代入反比例函数 （ ），得 k＝ •8＝4， ∴反比例函数的解析式为 y＝ ； 又∵点 Q（4，m）在该反比例函数图象上， ∴4•m＝4， 解得 m＝1，即 Q 点的坐标为（4，1）， 而直线 y＝－x＋b 经过点 Q（4，1）， ∴1＝－4＋b， 解得 b＝5， ∴直线的函数表达式为 y＝－x＋5； （2）联立 ， 解得 或 ， ∴P 点坐标为（1，4）， 对于 y＝－x＋5，令 y＝0，得 x＝5， ∴A 点坐标为（0，5）， ∴S△OPQ＝S△AOB－S△OBP－S△OAQ ＝ ×5×5－ ×5×1－ ×5×1 ＝ ． 点评：本题考查了点在图象上，点的横纵坐标满足图象的解析式以及求两个图象交点的方法 （转化为解方程组）；也考查了利用面积的和差求图形面积的方法． 54. （2011 四川遂宁，23，9 分）平面直角坐标系中，直线 AB 交 x 轴于点 A，交 y 轴于点 B 且与反比例函数图象分别交于 C、D 两点，过点 C 作 CM⊥x 轴于 M，AO=6，BO=3， CM=5．求直线 AB 的解析式和反比例函数解析式． 2 1 x ky = 0≠k 2 1 x 4    = +−= xy xy 4 5    = = 1 4 y x    = = 4 1 y x 2 1 2 1 2 1 2 15 考点：反比例函数综合题。 专题：函数思想。 分析：首先由过点 C 作 CM⊥x 轴于 M，得 CM∥OB，所以△AOB∽△AMC，可求出 AM，继 而得出点 A、B、C 的坐标，然后设解析式，代入坐标即可求出直线 AB 的解析式和反 比例函数解析式． 解答：解：由题意得 CM∥OB ∴ △AOB∽△AMC ∴ 即 ∴ AM=10 ∵ AO=6 ∴ MO=4 ∴点 C（4，5） A（－6，0） B（0，3） 设直线解析式 ∵过点 A（－6，0）和点 B（0，3） ∴ ，b=3 ∴ 设反比例解析 ∵过点 C（4，5） ∴ ∴ 点评：此题考查的知识点是反比例函数综合应用，关键是运用相似三角形求出点的坐标，用 待定系数法确定函数的解析式． CM BO AM AO = 5 3 AM 6 = bxky += 11 2 1=k 32 1 1 += xy x ky 2 2 = 202=k xy 20 2 =