挑战中考数学压轴题——几何综合题素质训练之正方形 16页

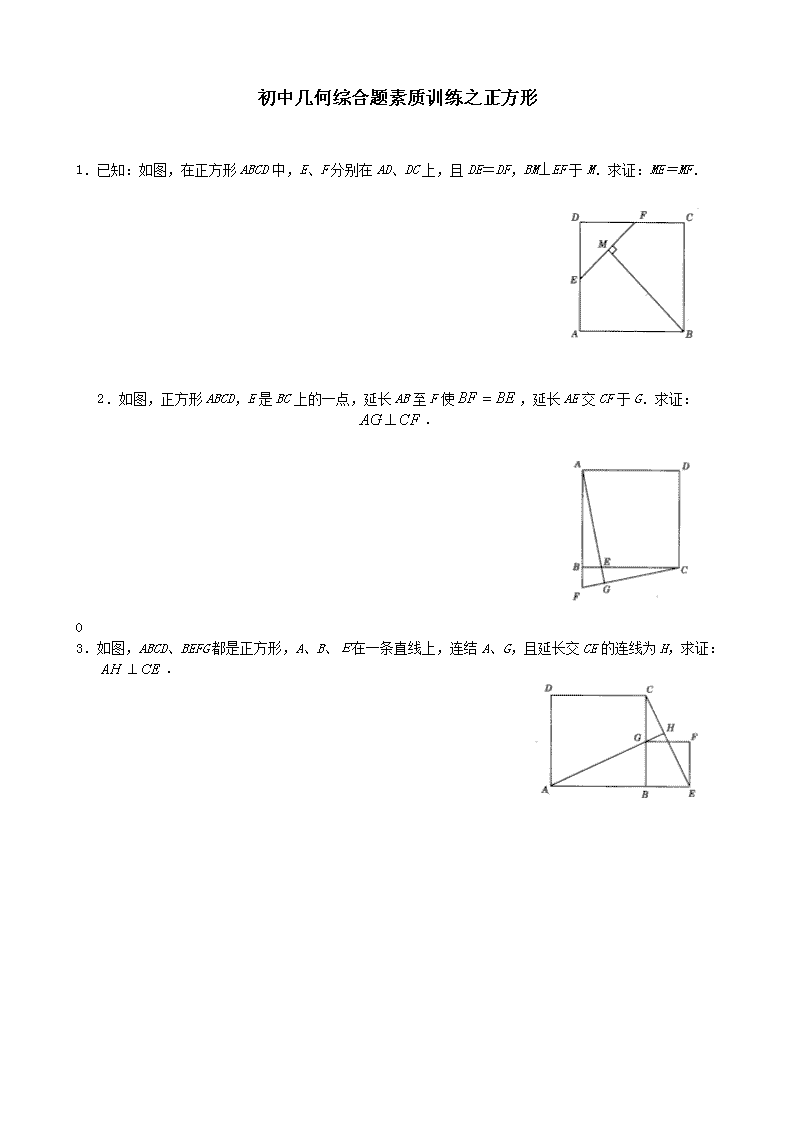
初中几何综合题素质训练之正方形 ‎1．已知：如图，在正方形ABCD中，E、F分别在AD、DC上，且DE＝DF，BM⊥EF于M．求证：ME＝MF．‎ ‎ ‎ ‎2．如图，正方形ABCD，E是BC上的一点，延长AB至F使，延长AE交CF于G．求证：．‎ ‎ 　　‎ ‎　‎ ‎　‎ ‎0‎ ‎3．如图，ABCD、BEFG都是正方形，A、B、Ｅ在一条直线上，连结A、G，且延长交CE的连线为H，求证：．‎ ‎ 　‎ ‎　‎ ‎4．如图，某同学参加数学兴趣小组活动，提供了下面3个有联系的问题，请你帮助解决：‎ ‎（1） 如图1，正方形中，作交于，交于，求证：；‎ ‎（2） 如图2，正方形中，点分别在上，点分别在上，且 ‎，求的值；‎ ‎（3） 如图3，矩形中，，，点分别在上，且，求 的值．‎ ‎ ‎ ‎5．已知：如图，正方形ABCD，P是BO上任意一点，DQ⊥AP，垂足是Q，交AC于R，‎ 求证：⑴、DP=CR．‎ ‎⑵、若P为OB延长线上一点，其它条件不变，那么上述的结论是否仍然成立，画图并证明.‎ ‎ ‎ ‎6．如图，已知ABCD是正方形，对角线AC与BD相交于O，，且分别与AO、BO交于M、N．求证：．‎ ‎ ‎ ‎　‎ ‎7．如图，已知正方形ABCD中，F为CD延长线上一点，于E，交AD于M．求：∠MFD的度数．‎ ‎ ‎ ‎8．已知：如图，正方形ABCD中，M为DC中点，交AC于E，交BC于F．求证：∠DMA=∠EMC．‎ ‎ ‎ ‎9．已知：如图，AM为△ABC的中线，四边形、ACFG均为正方形．求证：．‎ ‎ ‎ ‎10．已知：如图，正方形ABCD中，CE垂直于的平分线于E，AE交DC于F．求证：．‎ ‎ ‎ ‎11．已知：如图，正方形ABCD中，M是CD中点，E是CD上一点，且．‎ 求证：AE＝BC＋CE．‎ ‎ ‎ ‎12．已知：如图，正方形ABCD中，E、F分别为AB、BC的中点，CE、DF交于M．求证：AM=AD．‎ ‎ ‎ ‎13、如图正方形ABCD，以CD为边长向正方形内作等边△CDE,连BE交AC于F，连DF，‎ 求证：⑴ △ADF≌△ABF ⑵ 求∠AFD的大小 ⑶ 求证AF+DF=CF ‎14．（利用旋转处理正方形问题）‎ ‎△ABC是等腰直角三角形，∠C＝90°，M、N为斜边AB上两点，如果∠MCN＝45求证 AM2＋BN2 =MN2 ‎ ‎15、已知M、N分别在正方形ABCD的边BC、CD上，且∠MAN=45°‎ ‎⑴ 如图1求证：MN=DN+BN ‎⑵ 如图2，若点M、N分别在CB、DC的延长线上，∠MAN=45°，请探究：MN、BM、DN之间的关系 如果改∠MAN=45°顶点不在A点，而在正方形的中心O点处，其它的条件不变，请问MC、MB与MN之间的关系 ‎16、已知M、N分别在正方形ABCD的边BC、CD上，且MN=DN+BN ‎⑴ 如图1求∠MAN的度数 ‎⑵ 如图2，若AM、AN分别和BD交于E、F点，请探究：DE、EF、FB之间的关系 ‎⑶ 若点M、N分别在CB、DC的延长线上，∠MAN=45°MN、DN、BN之间的关系；请探究：DE、EF、‎ FB之间的关系画图证明 17、 如图正方形ABCD中，点O为对角线AC的中点，点P为正方形ABCD外的一点，且BP⊥CP ‎⑴ 如图1，求证BP+CP=OP ‎⑵ 如图2，当点P在正方形的内部时，问BP、CP、OP三者又存在什么样的关系？请证明 17、 正方形ABCD中，点O是对角线AC的中点，P是对角线AC上一动点，过点P作PF⊥CD于点F。如图1，当点P与点O重合时，显然有DF＝CF．‎ ‎⑴如图2，若点P在线段AO上（不与点A、O重合），PE⊥PB且PE交CD于点E。‎ a) ‎①求证：DF＝EF； ‎ b) ‎②写出线段PC、PA、CE之间的一个等量关系，并证明你的结论；‎ ‎⑵若点P在线段OC上（不与点O、C重合），PE⊥PB且PE交直线CD于点E。请完成图3并判断⑴中 的结论①、②是否分别成立？若不成立，写出相应的结论（所写结论均不必证明）‎ ‎19、如图，在边长为4的正方形ABCD中，点P在AB上从A向B运动，连接DP交AC于点Q．‎ ‎（1）试证明：无论点P运动到AB上何处时，都有△ADQ≌△ABQ；‎ ‎（2）当点在上运动到什么位置时，△ADQ的面积是正方形ABCD面积的；‎ ‎（3）若点P从点A运动到点B，再继续在BC上运动到点C，在整个运动过程中，当点P 运动到什么位置时，△ADQ恰为等腰三角形．‎ 20、 操作：如图1，把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上（CG＞BC），取线段AE的中点M。探究：线段MD、MF的关系，并加以证明。‎ 说明：‎ ‎（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求 至少写3步）；‎ ‎（2）在你经历说明（1）的过程之后，可以从下列①、②、③中选取一个补充或更换已知条件，完成 你的证明。‎ ‎①、DM的延长线交CE于点N，且AD＝NE；‎ ‎②、将正方形CGEF绕点C逆时针旋转45°（如图2），其他条件不变；‎ ‎③、在②的条件下且CF＝2AD。‎ 附加题：将正方形CGEF绕点C旋转任意角度后（如图3），其他条件不变。探究：线段MD、MF的关系，并加以证明。‎ ‎ ‎ 正方形，点为直线上一点，连，以为腰作等腰,连交于.‎ ‎⑴ 如图1，当点在线段上时，求的值，并证明 ‎⑵ 如图2若点在线段的延长线上，求的值，并证明 20、 如图，P为正方形ABCD边BC上一点，BG⊥AP于点G，在AP的延长线上取点E，使AG=GE，连接BE、CE.⑴求证 ： ‎ ‎⑵ ∠CBE的平分线交AE于N点，连接DN，求证：‎ ‎23、如图正方形ABCD中，P为CD上一动点，E为CB延长线上一点，且BE=DP，连接PE交AB、AC分 别于Q、N，∠CPE的平分线分别交AC、BC于M、F。‎ ‎（1）求证：AP=AM；‎ ‎（2）若AP=NE，求证：‎ ‎24、如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.‎ ‎⑴ 求证：△AMB≌△ENB；‎ ‎⑵ ①当M点在何处时，AM＋CM的值最小；‎ ‎②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；‎ ‎⑶ 当AM＋BM＋CM的最小值为时，求正方形的边长.‎ ‎ ‎ ‎25、M、N是正方形ABCD的边BC上的点，且BM=CN，CH⊥DN于H，CH的延长线交BD于Q，交AB于K，QM 与DN的延长线交于点P.‎ ‎⑴求证：AK=BN；‎ ‎⑵当H是DP的中点时，试探究线段CQ+BQ与PD的数量关系并证明，‎ ‎⑶在⑵的条件下，若正方形的边长为，请直接写出MN的长 ‎26、如图，四边形ABDM中，AB=BD，AB⊥BD，∠AMD=60°，以AB为边作等边△ABC，BE平分∠ABD交CD 于E，连ME.‎ ‎⑴ 求∠BEC的度数。‎ ‎⑵ 探究于之间的关系，并加以证明 ‎⑶若，则线段的长为 ‎ ‎ ‎