中考物理试题分类汇编之力学压轴题 33页

‎2015年中考物理试题分类汇编 ‎1、（2015内江）2014年4月14日，为寻找失联的MH370航班，启用了“蓝鳍金枪鱼﹣21”（简称“金枪鱼”）自主水下航行器进行深海搜寻。其外形与潜艇相似（如图16甲所示），其相关参数为：体积1m3、重量7500N，最大潜水深度4500m，最大航速7.4km/h（为简化计算，不考虑海水密度变化，海水密度ρ取1.0×103kg/m3，g取10N/kg）。‎ （1） 假设“金枪鱼”上有面积为2×10-3m2的探测窗口，当它下潜至4000m深度处时，该探测 窗口承受海水的压力是多少？‎ ‎（2）“金枪鱼”搜寻任务完成后，变为自重时，能静止漂浮在海面上，求此时“金枪鱼”露出海面的体积为多大？‎ ‎（3）若上述漂浮在海面的“金枪鱼”，由起重装置将其匀速竖直吊离海面。从某时刻计时起，起重装置拉力的功率随时间变化的图象如图16乙所示，图中P3=3P1。请分析出t3时刻起重装置对“金枪鱼”拉力，并求出t1时刻起重装置对“金枪鱼”拉力（不考虑水的阻力）。‎ 图16‎ ‎【解答】‎ ‎（1）当它下潜至4000m深度处受到海水的压强：‎ P=ρgh=1.0×103kg/m3×10N/kg×4000m=4×107Pa 探测窗口承受海水的压力：‎ 由P=F/S得F=PS=4×107Pa×2×10-3m2=8×104N ‎ （2）解：“金枪鱼”搜寻任务完成后，静止漂浮在海面上，所以有F浮=G=7500N。‎ ‎ 由F浮=ρ液gV排得V排=F浮/（ρ液g）=7500N/（1.0×103kg/m3×10N/kg）=0.75m3‎ ‎ 露出海面体积为：V露=V﹣V排=1m3﹣0.75m3=0.25m3‎ ‎ （3）解：由图象分析知，在t3时刻“金枪鱼”离开水面，此时起重装置对“金枪鱼”的拉力等于“金枪鱼”的重力，即F3 =G=7500N ‎ 由于起重装置吊起“金枪鱼”是匀速竖直离海面，所以速度保持不变即v1=v3，由P=Fv， ‎ ‎ 得P1=F1v1，P3=F3v3，又P3=3P1，所以有F3=3F1‎ ‎ 所以F1=F3=×7500N=2500N ‎2．（2015绵阳）我国南宋远洋商贸船“南海一号”于2007年成功打捞出水，为复原我国 海上丝绸之路历史提供了极其珍贵的实物资料，采用沉井包裹沉船的整体打捞方式，在世界水下考古也是一大创新。某同学为了体验“南海一号”的打捞过程，特利用滑轮组从水下打捞一重物。‎ 如图所示，用一个底面积S=0.05m2、高h=0.2m的长方体形状的重物模拟“南海一号”，该同学站在岸边拉动绳子自由端，使重物从水底开始向上运动。假定重物一直做竖直向上的匀速直线运动，并经历三个运动阶段：第一阶段，从重物在水度开始运动到重物的上表面刚露出水面，绳对重物的拉力 F1=140 N，用时t1=40s；第二阶段，从重物上表面刚露出水面到其下表面刚离开水面，用时t2=4s；第三阶段，从重物下表面离开水面后在空中上升。已知动滑轮所受重力G0=60 N，ρ水=1.0×103kg/m3， g=10N/g，不计绳重、轮与轴之间的摩擦及水的阻力，不考虑重物出水前后质量的变化。求：‎ ‎①在第一阶段运动中，水对重物的浮力F浮为多大?‎ ‎②在第一阶段运动中，绳对重物做功W1为多大?‎ ‎③滑轮组在第一阶段运动中的机械效率η1和第三阶段运动中的机械效率η3分別为多大?‎ ‎【解答】‎ ① 在第一阶段中V排=V物=Sh=0.05m2×0.2m=0.01m3， 则水对重物的浮力：F浮=ρ水gV排=1.0×103kg/m3×10N/kg×0.01 m3=100N；‎ ② 在第二阶段，从重物上表面刚露出水面到其下表面刚离开水面，用时t2=4s，上升高度为物体的高h，‎ 物体上升的速度 在第一阶段中，重物上升的高度h1=vt1=0.05m/s×40s=2m 绳对重物做功W1=F1 h1=140 N×2m=280J ‎③ 由于不计绳重、轮与轴之间的摩擦及水的阻力，以动滑轮为研究对象，受3段绳子向上的拉力、动滑轮的重力、下方绳子对动滑轮向下的拉力。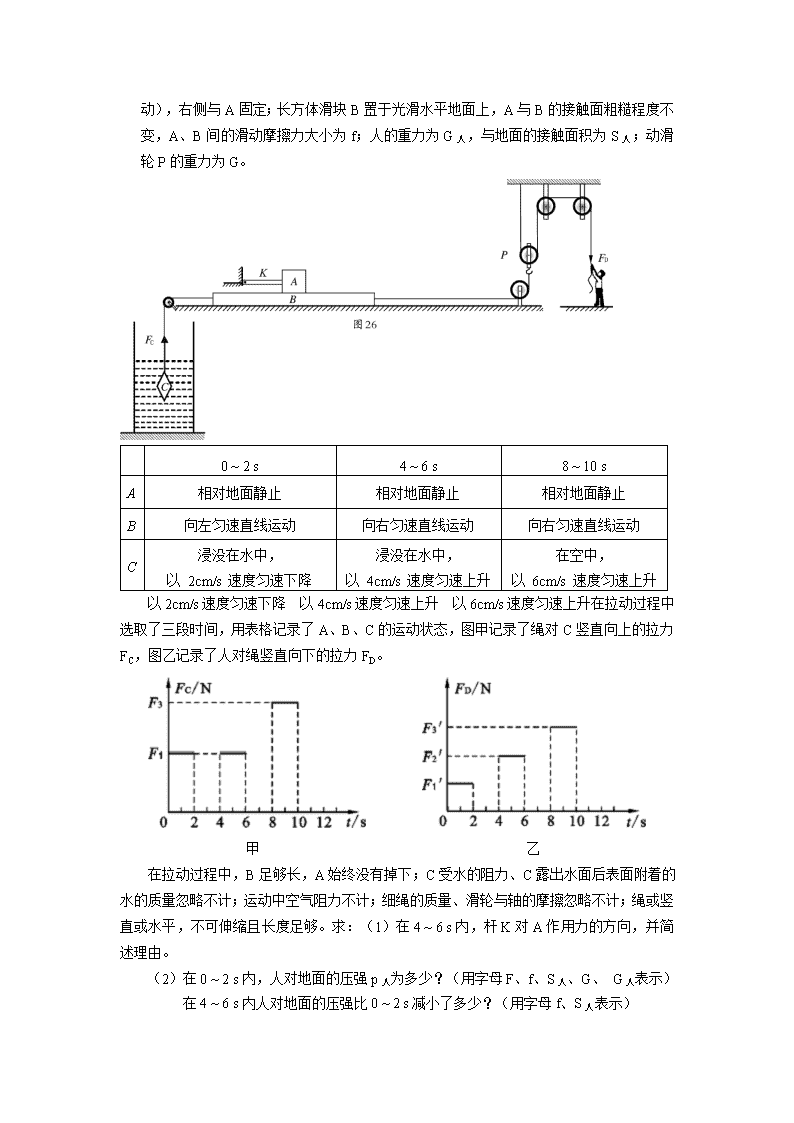‎ 在第一阶段中，人对绳子自由端的拉力 机械效率 在第一阶段中，以重物为研究对象，受向下的重力G物、向上的拉力F1、向上的浮力F浮，‎ 由平衡条件有：G物=F1+F浮= 140N+100N=240N，‎ 在第三阶段中，设重物上升高度为h3，由于不计绳重、轮与轴之间的摩擦及水的阻力，‎ 此时机械效率 答：①在第一阶段运动中，水对重物的浮力F浮为100N； ②在第一阶段运动中，绳对重物做功W1为280J． ③在第一阶段运动中的机械效率η1和在第三阶段运动中的机械效率η3分别为70%、80% .‎ ‎3．（2015成都B卷）如图所示，轻质硬杆K左侧与墙体相连（可自由转动，不能水平移 动），右侧与A固定；长方体滑块B置于光滑水平地面上，A与B的接触面粗糙程度不变，A、B间的滑动摩擦力大小为f；人的重力为G人，与地面的接触面积为S人；动滑轮P的重力为G。‎ ‎0 ~ 2 s ‎4 ~ 6 s ‎8 ~ 10 s A 相对地面静止 相对地面静止 相对地面静止 B 向左匀速直线运动 向右匀速直线运动 向右匀速直线运动 C 浸没在水中，‎ 以 2cm/s 速度匀速下降 浸没在水中，‎ 以 4cm/s 速度匀速上升 在空中，‎ 以 6cm/s 速度匀速上升 以2cm/s速度匀速下降 以4cm/s速度匀速上升 以6cm/s速度匀速上升在拉动过程中选取了三段时间，用表格记录了A、B、C的运动状态，图甲记录了绳对C竖直向上的拉力FC，图乙记录了人对绳竖直向下的拉力FD。‎ ‎ ‎ 甲 乙 ‎ 在拉动过程中，B足够长，A始终没有掉下；C受水的阻力、C露出水面后表面附着的水的质量忽略不计；运动中空气阻力不计；细绳的质量、滑轮与轴的摩擦忽略不计；绳或竖直或水平，不可伸缩且长度足够。求：（1）在4 ~ 6 s内，杆K对A作用力的方向，并简述理由。扬州大学附属中学东部分校姜雪峰编制 ‎ （2）在0 ~ 2 s内，人对地面的压强p人为多少？（用字母F、f、S人、G、 G人表示）‎ ‎ 在4 ~ 6 s内人对地面的压强比0 ~ 2 s减小了多少？（用字母f、S人表示）‎ ‎ （3）若C的重力GC=40N， F3= 2 F1， 且 F3′∶F2′∶F1′= 3∶2∶1，则C在0 ~ 2 s内所受的浮力为多少？人在8 ~ 10 s内做功的功率为多少？‎ ‎【解答】（1）A受到杆 K 的作用力FK向左．因为在4～6s内，A相对地面静止，B向右匀速直线运动，A相对于B向左运动，可知B对A摩擦力f′向右，A处于静止状态，水平方向必定受平衡力作用，所以杆K对A作用力向左．‎ ‎（2）在0～2s内：B向左匀速直线运动，在水平方向受C的向左的拉力，A向右的摩擦力及P向右的摩擦力，则FP+f=F1，可得FP=F1﹣f；‎ 由图知，滑轮组由2段绳子承担物重，所以FD=（FP+GP）=×（F1﹣f+GP），‎ 则人对地面的压力F=G人﹣FD=G人﹣×（F1﹣f+GP），‎ 人对地面的压强：p==；‎ 在4～6s内：B向右右匀速直线运动，受到A的摩擦力向左，则F1+f=FP′；‎ 则FD′=（FP′+GP）=×（F1+f+GP）；‎ 人对地面的压力F′=G人﹣FD′=G人﹣（F1+f+GP）；‎ 则△F=F﹣F′=G人﹣×（F1﹣f+GP）﹣[G人﹣（F1+f+GP）]=f 则△p==；‎ ‎（3）以C为研究对象：由图2知，在8～10s内，物体在空气中，则F3=GC=40N 由题意知，F1=F3=×40N=20N 在0～2s内有，物体C受浮力、绳的拉力、和重力作用，则 F1+F浮=GC 所以F浮=GC﹣F1=40N﹣20N=20N 以B为研究对象：‎ 在4～6s内有 F1+f=2 F2′﹣GP 在8～10s内有 F3+f=2 F3′﹣GP F3﹣F1=2（F3′﹣F2′）‎ 又因为F3′：F2′=3：2；‎ 所以F3﹣F1=2×F3′=F3′‎ F3′=×（F3﹣F1）=×（40N﹣20N）=30N 在8～10s 内，人做功的功率：‎ P===F3′v=30N×0.12m/s=3.6W．‎ 答：（1）K对A作用力向左；理由如上所述；‎ ‎（2）在0～2s内，；在4～6s内人对地面的压强比0～2s减小了；‎ ‎（3）C在 0～2s内所受的浮力为20N；人在8～10s内做功的功率为3.6W．‎ ‎4．（2015泸州）图甲是建造长江大桥是使用起吊装置（图中未画出）的钢缆绳拉着实心圆柱体A距江面某一高度处沿竖直方向匀速下降，在下降到江底之前，始终保持0.2m/s的速度不变。图乙是A下降到江底之前钢缆绳对A的拉力F的随时间t变化的图像。‎ ‎（取江水的密度为ρ =1.0×103kg/m3 ，g取10N/kg）求： ‎ ‎（1）圆柱体A下降过程中，重力的功率？ ‎ ‎（2）圆柱体A的密度？ ‎ ‎（3）当圆柱体A下降到江底（江底视为水平），卸下钢缆绳后，圆柱体A对江底的压强？‎ ‎【解答】‎ ‎（1）圆柱体在江面上匀速下降时，重力G=F1=3×104N .‎ 重力的功率P=Gv=3×104N×0.2m/s=6×103W （1） 当A完全浸入水中时，拉力F2=1×104N A受到的浮力：F浮=G-F2=3×104N-1×104N=2×104N，‎ A的体积V=V排=‎ A的密度 （2） A从刚接触江面到浸没用的时间t=15s-10s=5s ‎ A的高度h=vt=0.2m/s×5s=1m ‎ A的底面积 圆柱体A沉底且卸下钢缆绳后，A对江底的压力F=G-F浮=3×104N-2×104N=1×104N 圆柱体A对江底的压强 ‎5．（2015德阳）如图甲所示底面积为0.2m2，高0.2m的质量均匀的长方体物体A，放置在水平地面上，对地面的压强为6×103Pa；一质量为80kg的工人站在水平地面上，用如图乙所示的滑轮组把A运到高处，工人用大小为F1的竖直拉力拉绳使A以10cm/s的速度匀速上升，这时地面对工人的支持力为N1，工人匀速拉绳的功率为P，滑轮组的机械效率为η1．若工人以相同的功率用大小为F2的竖直拉力拉绳使另一物体B以12.5cm/s的速度匀速上升，这时地面对工人的支持力为N2，滑轮组的机械效率为η2．已知N1：N2=3：4，η1：η2=16：15．（g取10N/kg）求：‎ ‎（1）物体A的密度；‎ ‎（2）工人拉绳的功率P；‎ ‎（3）用滑轮组提升B时滑轮组的机械效率η2．‎ ‎【解答】‎ ‎（1）由p==可知，G=pS=6×103Pa×0.2m2=1200N，‎ 由G=mg可知，A的质量：mA===120kg，‎ A的密度：ρ= = =3000kg/m3；‎ ‎（2）对工人，由平衡条件得：F拉+N=m人g=80kg×10N/kg=800N，‎ 则：N1=800N﹣F1，N2=800N﹣N2，‎ 由题意可知：N1：N2=3：4，则：4F1﹣3F2=800N﹣﹣﹣①‎ 提升物体时的功率相等，P=F1v1=F2v2，解得：F1：F2=5：4﹣﹣﹣②‎ 由①②解得：F1=500N，F2=400N，‎ 工人拉绳子的功率：P=F1v1=500N×0.1m/s×3=150W；‎ ‎（3）滑轮组效率：η==，由题意可知：η1：η2=16：15，‎ η2=η1=×=×=75%；‎ 答：（1）物体A的密度为3000kg/m3；‎ ‎（2）工人拉绳的功率P为150W；‎ ‎（3）用滑轮组提升B时滑轮组的机械效率η2为75%．‎ ‎6．（2015广安）新农村建设让农村面貌焕然一新。许多楼房顶部装有自动供水水箱，箱体重1250N ‎，与水平楼顶接触面积为1.5m2。为了控制进水量，在水箱顶部安装压力传感器，如图（14）所示，A物体通过细线与压力传感器相连接，压力传感器相等于拉线开关，A的密度是2.5×103kg/m3，A重为25N。当压力传感器受到竖直向下的拉力等于25N时闭合，电动水泵向水箱注水；当拉力等于15N时断开，电动水泵停止向水箱注水。‎ ‎（1）求未装水时整个水箱对楼顶的压强是多少？（压力传感器及连接线质量不计，g取10N/kg）‎ ‎（2）通过计算说明当水面与A上表面相平时，电动水泵能否停止注水？（g取10N/kg，连接线体积不计）‎ ‎【解答】‎ ‎7．（2015凉山州）如图所示，水平桌面的正中央放着三个底面积均为500cm2的薄壁容器，容器内装有适当的水，在圆柱形的乙容器中放入一个密度为0.6×103kg/m3，体积为1dm3的木块漂浮在水面，现用力F将木块刚好压没于水中静止，水未溢出。求：‎ ‎（1）静止时所施加的压力F的大小；‎ ‎（2）乙容器中木块被压没后和没有放入木块时相比水对容器底部的压强增加了多少？‎ ‎（3）若也将木块压没于甲、丙两容器中（木块未触底、水未溢出），静止时判断三容器中水对容器底部的压强增加量的大小关系。‎ ‎【解答】（1）木块重力G木=mg=ρ木Vg=0.6×103kg/m3×1×10﹣3m3×10N/kg=6N．‎ 由于木块完全浸没，则V排=V=1dm3=1×10-3m3，‎ F浮=ρ水gV排=1000kg/m3×10N/kg×1×10﹣3m3=10N；‎ 由于F浮=F+G，所以，所施加的压力：F=F浮﹣G=10N﹣6N=4N；‎ ‎（2）由于乙容器是柱状容器，则木块被压没后和没有放入木块时水对容器底部的增加的压力即为木块浸没时所受浮力，即△F乙=F浮=10N，‎ 所以水对容器底面增加的压强为△p乙===200Pa；‎ ‎（3）若也将木块压没于甲、丙两容器中（木块未触底、水未溢出），由于甲的形状是上大下小，故水面升高的高度最小；而丙的形状是上小下大，故水面升高的高度最高；‎ 所以根据可知：△p甲＜△p乙＜△p丙．‎ 说明：第2、3两小题的解法不止一种，用其它方法也行。‎ ‎8．（2015遂宁）某兴趣小组用如图甲所示的滑轮组（物体与动滑轮用绳子a连接）匀速拉动放在同一水平面上的不同物体，物体受到的摩擦力从200N开始逐渐增加，直到组装滑轮组的绳子b被拉断，每次物体拉动的距离均为2m。 通过实验绘出了该滑轮组机械效率随物体受到摩擦力大小变化的关系图像如图乙。（不计绳重和绳与滑轮间的摩擦）求：‎ ‎（1）动滑轮重力；‎ ‎（2）当滑轮组的机械效率为80%，物体以0.2m/s的速度匀速运动时，该滑轮组的 有用功率；‎ （1） 一个重500N的同学利用该滑轮组，想独自用竖直向下的力拉断绳子b，请你通过计算分析他能否实现？‎ ‎【解答】（1）由图乙可知，当f1=200N时， ﹪‎ ‎ W有用1 = fs ‎ 由于不计绳重及绳与滑轮间的摩擦， W额外 = G动s ‎ ∴ W总1 = fs+ G动s ‎ ∵ ‎ ‎ ∴ ﹪‎ ‎ ∴ G动 = 200N ‎ ‎ （2）当﹪时，﹪‎ ‎∴ f2 = 800N ‎ ‎∴ W有用2 = f2s = 800N×2m = 1600J ‎ ‎ ∵ ‎ ‎∴ ‎ ‎∵ ‎ ‎∴ ‎ ‎ 另解：当﹪时，‎ ‎∴ f2 = 800N ‎ ‎∵ ‎ ‎∴ ‎ ‎ （3）由图乙可知，当f3=1600N时，绳子刚好被拉断，由于不计绳重及绳与滑轮间的摩擦，且物体做匀速直线运动 ‎ ∴ 绳b承受的最大拉力 ‎ ‎∴ ‎ 因为人的重力为500N，竖直匀速拉动，所以绳子对人的最大拉力为人的重力，根据力的作用是相互的，故人给绳子的最大拉力为500N，由于绳子b承受的最大拉力大于人给绳子的最大拉力，所以该同学不能拉断绳子b 。‎ ‎9．（2015玉林）如图是利用电子秤显示水库水位装置的模型图。该装置主要由两个重力均为20N的动滑轮、长方体物块A和B以及轻质杠杆MN组成，物块A通过细绳与滑轮相连，物块B通过细绳与杠杆相连。杠杆可以绕支点O在竖直平面内转动，杠杆始终在水平位置平衡，且OM：ON=1：4。已知物块A的重力GA=1500N，底面积S=0.01m2，高H=10m，物块B的重力GB=100N。一切摩擦均忽略不计，g取10N/kg。当物块A有五分之一露出水面时，水库水位刚好达到警戒水位。求：‎ ‎（1）当达到警戒水位时，物块A底部受到水的压强；‎ ‎（2）当达到警戒水位时，物块A所受的浮力大小；‎ ‎（3）当水位上涨超出警戒水位2.5m时，电子秤的示数。‎ ‎【解答】（1）当达到警戒水位时，物块A有五分之一露出水面，则底部所处的深度：‎ h=（1﹣）H=×10m=8m，‎ 底部受到水的压强：p=ρgh=1×103kg/m3×10N/kg×8m=8×104pa．‎ ‎（2）当达到警戒水位时，物块A排开水的体积V排=Sh=0.01m2×8m=0.08m3，‎ 物块A所受的浮力：F浮=ρ水V排g=1×103kg/m3×0.08m3×10N/kg=800N；‎ ‎（3）由于水库水位刚好达到警戒水位物块A露出水面的长度为H=h=10m﹣8m=2m，‎ 所以当水位上涨超出警戒水位2.5m时，物块A已经浸没，则根据阿基米德原理可知：‎ 此时物块A所受的浮力F浮=ρ水Vg=ρ水SHg=1×103kg/m3×0.01m2×10m×10N/kg=1000N；‎ 滑轮与转轴的摩擦、杠杆与轴的摩擦均忽略不计，‎ 物块A对滑轮C的拉力FA拉=GA﹣F浮=1500N﹣1000N=500N；‎ 根据受力平衡可知：2FC=G动+FA拉，‎ 所以，FC=（G动+FA拉）=（20N+500N）=260N，‎ 滑轮D根据受力平衡可知：2FD=G动+FC，‎ 所以，FD=（G动+FC）=（20N+260N）=140N；‎ 由于力的作用是相互的，则FM=FD=140N；‎ 根据杠杆平衡条件可知：FMLOM=FNLON，‎ 所以，FN===35N；‎ 对于物块B，根据力的平衡条件可知：GB=FN+F支，‎ 所以F支=GB﹣FN=100N﹣35N=65N．‎ 电子秤的示数=F压= F支=100N﹣35N=65N.‎ ‎10．（2015来宾）如图所示为一种蓄水箱的人工放水装置，AOB是以O点为转轴的轻质杠杆，AO呈水平状态，A、O两点间的距离为40cm，B、O两点间的水平距离为10cm，竖直距离为7cm。K是一轻质、横截面积为100cm2的盖板（恰好堵住出水口），它通过细绳与杠杆的A端相连。在水箱右侧的水平地面上，重为600N的人通过滑轮组拉动系在B点呈竖直状态的绳子，可以控制出水口上的盖板。若水箱中水深为50cm，当盖板恰好要被拉起时，水平地面对人的支持力为490N，人对绳子的拉力为F1，绳子对B点的拉力为F2，滑轮组的机械效率为η。盖板的厚度、绳重及绳与滑轮间的摩擦均可忽略不计，人对绳的拉力与人所受重力在同一直线上（g取10N/kg）。求：‎ ‎（1）水箱中水深为50cm时，盖板上表面所受水的压强和压力；‎ ‎（2）人对绳子的拉力F1和绳子对B点的拉力F2；‎ ‎（3）滑轮组的机械效率η；‎ ‎（4）若与杠杆A、B两端连接的细绳足够结实，当水位至少达到多高时，人将无法拉起盖板。‎ ‎【解答】‎ ‎（3）动滑轮C上的绳子对杠杆及盖板所做的功为有用功，动滑轮上绳子的段数n=2.‎ ‎∴滑轮组的机械效率 ‎11．（2015贵港）一带阀门的圆柱形容器，底面积是200cm2，装有12cm深的水，正方体M边长为10cm，重20N，用细绳悬挂放入水中，有的体积露出水面，如图所示，试求：‎ ‎（1）正方体M的密度；‎ ‎（2）正方体M受到的浮力以及此时水对容器底部的压强；‎ ‎（3）若从图示状态开始，通过阀门K缓慢放水，当容器中水面下降了2cm时，细绳刚好被拉断，则细绳能承受的最大拉力是多少？（g取10N/Kg，水的密度为1.0×103kg/m3）．‎ 解：（1）正方体M的质量mM===2kg，‎ 体积为VA=L3=（10cm）3=1000cm3=1×10﹣3m3，‎ 所以，密度ρA===2×103kg/m3；‎ ‎（2）由于用细绳悬挂放入水中，有的体积露出水面，则：‎ V排1=（1﹣）VA=×1×10﹣3m3=8×10﹣4m3，‎ 受到的浮力为：F浮1=ρ水gV排1=1.0×103kg/m3×10N/kg×8×10﹣4m3=8N；‎ 设正方体悬挂放入水中后水深为h′，则有Sh′=Sh+V排1，‎ 则h′=h+=0.12m+=0.16m．‎ 此时水对容器底部的压强：p=ρ水gh′=1.0×103kg/m3×10N/kg×0.16m=1.6×103Pa．‎ ‎（3）原来正方体M浸入水中深度为h1=（1﹣）L=×10cm=8cm，‎ 水面下降2cm时正方体M浸入水中深度为h2=h1﹣2cm=8cm﹣2cm=6cm，‎ 则V排2=h2L2=6cm×（10cm）2=600cm3=6×10-4m3，‎ F浮2=ρ水gV排2=1.0×103kg/m3×10N/kg×6×10-4m3=6N；‎ 当绳子刚被拉断时有：Fm+F浮2=G，‎ 所以细绳能承受的最大拉力Fm=G﹣F浮2 =20N﹣6N=14N．‎ 答：（1）正方体M的密度为2×103kg/m3；‎ ‎（2）正方体M受到的浮力为8N；此时水对容器底部的压强为1.6×103Pa；‎ ‎（3）当容器中水面下降了2cm时，细绳刚好被拉断，细绳能承受的最大拉力是14N．‎ ‎12．（2015南宁）体重为600N的小聪用如图19所示的滑轮组来竖直提升物体A。当A以0.1m/s的速度匀速上升时，小聪对绳子的拉力F为400N，滑轮组的机械效率为80%（不计摩擦及绳重）。求： （1）拉力F的功率； （2）物体A受到的重力； （3）小聪拉动绳子前后对地面的压强之比； （4）小聪使用该滑轮组能提起物体的最大重力。‎ ‎【解答】‎ ‎（1）由图通过动滑轮绳子的段数n=3，物体A匀速上升，‎ 拉力F的功率：P=Fv=Fnv物=400N×3×0.1m/s=120W；‎ ‎（2）根据η===，‎ 物体A受到的重力：G=ηnF=80%×3×400N=960N；‎ ‎（3）小聪拉动绳子前对地面压力F=G人=600N，‎ 小聪拉动绳子后对地面压力F′=G人﹣F=600N﹣400N﹣200N，‎ 小聪拉动绳子前后对地面的压强之比：====；‎ ‎（4）不计摩擦及绳重，F=（G物+G动），‎ 提起A时，G动=3F﹣GA=3×400N﹣960N=240N，‎ 小聪对绳子自由端拉力最大等于他的重力，即F最大=G人=600N，‎ 此时提起物体的重力最大：G最大=3F﹣G动=3×600N﹣240N=1560N．‎ 答：（1）拉力F的功率为120W；‎ ‎（2）物体A受到的重力为960N；‎ ‎（3）小聪拉动绳子前后对地面的压强之比3：1；‎ ‎（4）小聪使用该滑轮组能提起物体的最大重力为1560N。‎ ‎14．（2015达州）某工人用如图所示的装置把一重1200N的箱子从斜面底端匀速拉到顶端用时10s，已知斜面长6m，高2m，此装置的机械效率为80%（滑轮重、绳重、滑轮与绳之间的摩擦均不计）。求：‎ ‎（1）拉力F；‎ ‎（2）拉力F做功的功率；‎ ‎（3）箱子与斜面间的摩擦力。‎ 说明：本题的装置为斜面与动滑轮的组合机械，难点是第3问求摩擦力。‎ ‎【解答】（1）物体从底端到顶端的路程为L，则绳子自由端移动的距离为2L。‎ 此装置的机械效率 ‎∴拉力F=‎ ‎（2）拉力F做的功W总=Fs绳=250N×2×6m=3000J 拉力F做功的功率 ‎（3）有用功W有=Gh=1200N× 2m=2400J 额外功W额= W总- W有=3000J-2400J=600J ‎∵滑轮重、绳重、滑轮与绳之间的摩擦均不计，‎ ‎∴W额= G动L 则动滑轮的重 ‎15、（2015上海）如图11 所示，薄壁圆柱形容器甲和圆柱体乙置于水平地面上。容器甲足够高、底面积为5×10-2m2，盛有质量为5 千克的水。圆柱体乙的重力为160 牛，底面积为8×10-2m2。‎ ‎①求容器甲内水的体积V水；‎ ‎②求圆柱体乙对水平地面的压强 p乙； ‎ ‎③若将一物块A 分别浸没在容器甲的水中、放在圆柱体乙上表面的中央时，水对容器甲底部压强的变化量与圆柱体乙对水平地面压强的变化量相等。求物块A的密度 ρA。‎ ‎【解答】‎ ‎17、（2015天津）底面积为S0的圆柱形薄壁容器内装有密度为ρ0的液体，横截面积为S1的圆柱形木块由一段非弹性细线与容器底部相连，且部分浸入液体中，此时细线刚好伸直，如图19所示，已知细线所能承受的最大拉力为T，现往容器中再缓慢注入密度为ρ0的液体，直到细线刚好被拉断为止，请解答下列问题：‎ ‎（1）画出细线刚好伸直时，木块在竖直方向上的受力示意图；‎ ‎（2）导出细线未拉断前，细线对木块拉力F与注入液体质量m之间的关系式；‎ ‎（3）求出细线刚好被拉断时与细线断后容器中液面恢复稳定时，容器底部所受液体压强的变化量。‎ ‎【解答】‎ ‎2015年中考物理试题分类汇编—力学压轴题（二）‎ ‎1、（2015郴州）如图是一厕所自动冲水装置，圆柱体浮筒A与阀门C通过杆B连接，浮筒A的质量为 1kg，高为 0.22m，B杆长为 0.2m，阀门C的上表面积为 25 cm2 ，B和C的质量、厚度、体积及摩擦均忽略不计，当 A露出 0.02m 时，C恰好被A拉开，实现了自动冲水（g 取 10N/kg）。求： ‎ ‎（1）刚拉开阀门C 时，C 受到水的压强和压力； ‎ ‎（2 ）此时浮筒A 受到的浮力； ‎ ‎（3 ）浮筒A 的密度。 ‎ ‎【解析】（1）阀门C处水的深度h=h浸+L=(0.22m-0.02m)+0.2m=0.4m 水对阀门C的压强 水对阀门C的压力 ‎（2）∵C恰好被A拉开，∴浮筒A对阀门C的拉力 浮筒A的重 此时浮筒受向上的浮力、向下的重力和向下的拉力，‎ ‎∴浮筒A受到的浮力 ‎（3）浮筒A排开水的体积 浮筒A的底面积 浮筒A的体积 浮筒A的密度 ‎2、（2015株洲）一根金属棒AB置于水平地面上，今通过弹簧测力计竖直地将棒的右端B缓慢拉起，如图甲所示。在此过程中，弹簧测力计对棒所做的功W与B端离开地面的高度x的关系如图乙所示。请根据图象解答下列问题。‎ ‎（1）该金属棒的长度l = m。‎ ‎（2）在B端拉起的过程中，当x1=0.6m时，测力计的示数为F1= N；当x2=1.6m时，测力计的示数为F2= N。‎ ‎（3）求金属棒的重心到A端的距离d。‎ ‎【解析】本题的难点是看懂图像，从图像中获取有用信息。‎ ‎（1）由图乙可知，两段图线均为倾斜直线，说明做功与移动的竖直距离成正比；而第2段图线更陡一些，说明拉力更大，原因是此时金属棒已经离开地面，拉力等于金属棒的重了。‎ 由此可知，B端离开地面的高度为1.2m时，金属棒即将离开地面，所以金属棒长1.2米；‎ ‎（2）图乙中x为0～1.2m过程中，金属棒被提起的高度h1=1.2m， ‎ 对金属棒所做的功W1=3.6J，‎ ‎∵W1=F1h1，∴拉力F1===3N；‎ 图乙中x为1.2m～1.6m过程中，金属棒被提起的高度h2=1.6m -1.2m=0.4m， ‎ 对金属棒所做的功W2=5.6J -3.6J=2J ‎∵W2=Gh2，∴金属棒的重G==5N，则F2=G=5N；‎ ‎（3）金属棒未提离地面时，根据相似三角形知识可知，力臂之比 根据杠杆平衡条件有F1l1=Gl2，即F1l棒=Gd；‎ 则重心到A端的距离d===0.72m．‎ 答：（1）1.2；‎ ‎（2）3；5；‎ ‎（3）金属棒的重心到A端的距离d为0.72m．‎ ‎3、（2015襄阳）如图所示，用滑轮组匀速提起1200N的重物，拉力做功的功率为1500W， 绳子的自由端向下拉的速度为3m/s，地面对人的支持力为N1，不计绳重和摩擦。‎ ‎（1）滑轮组中有几股绳子承担重物？作用在绳自由端的拉力是多少？‎ ‎（2）滑轮组的机械效率是多少？‎ ‎（3）若用此滑轮组匀速提起2400N的重物时，地面对人的支持力为N2，作用在绳自由端的拉力是多少？若N1:N2=5:1时，人的重力是多少？‎ ‎【解析】‎ 由图可知，n=3，‎ ‎∵，‎ ‎∴F拉===500N；‎ ‎（2）机械效率：η=×100%=×100%=×100%=×100%=80%；‎ ‎（3）不计绳重和摩擦，则F拉=（G动+G）‎ G动=3F拉﹣G=3×500N﹣1200N=300N 提起2400N的重物时，F拉′=（G动+G′）=（300N+2400N）=900N 人拉绳子的力与绳子拉人的力是相等的，‎ 人受3个力即向下的重力、向上的拉力、向上的支持力，‎ 因此有支持力N=G人﹣F拉 N1=G人﹣500N ①‎ N2=G人﹣900N ②‎ N1：N2=5：1 ③‎ 所以（G人﹣500N）：（G人﹣900N）=5：1‎ 解得：G人=1000N．‎ 答：（1）滑轮组中有3股绳子承担重物，作用在绳自由端的拉力是500N；‎ ‎（2）滑轮组的机械效率是80%；‎ ‎（3）若用此滑轮组匀速提起2400N的重物时，地面对人的支持力为N2，作用在绳 自由端的拉力是900N，若N1：N2=5：1时，人的重力是1000N．‎ ‎4、（2015武汉）在建的杨泗港长江大桥是武汉市第十座长江大桥，大桥的两个桥塔均为钢沉井基础，其中2号桥塔的钢沉井在距桥位上游20公里的工厂拼装完成后，采用气囊法整体下水，是世界上同类方法下水质量最大的钢沉井．（ρ江水=1.0×103kg/m3 ρ钢=7.9×103kg/m3）‎ ‎（1）如图1所示，在钢沉井的底部两侧塞满气囊，松开固定的钢沉井的钢索后，钢沉井便顺着倾斜的江滩滑入水中．钢沉井入水后能自己滑行数百米，这是由于　 　．托在钢沉井底部的气囊充气成圆筒状是为了　 　．‎ ‎（2）钢沉井下水后，依靠拖船将其拖行至指定位置．当拖船对钢沉井输出的总功率为5000kW时，1min内将钢沉井匀速拖行了120m，试估算这段时间内江水对钢沉井的阻力．‎ ‎（3）工人们将钢板焊接成有18个大小相同的方形孔的钢沉井，其俯视图如图2所示．钢沉井的长、宽和高分别为77m、40m和23m，质量为6225t．经测算，这样的钢沉井自行滑入江中稳定后，水面下的高度会达到7.5m．为了让钢沉井在江中被拖行时能顺利通过一些浅滩，下水前用质量为31t的钢板在钢沉井底部将一些方形孔密封起来，使钢沉井水面下的高度降到了3.2m．请求出钢沉井底部被密封的方形孔的个数．‎ ‎【解析】‎ ‎（1）钢沉井便顺着倾斜的江滩滑入水中后，由于具有惯性，会继续向前运动；‎ 托在钢沉井底部的气囊充气成圆筒状，用利用滚动代替滑动以减小摩擦；‎ ‎（2）拖船将钢沉井匀速拖行，受到的拉力与阻力是一对平衡力，即F=f，‎ 拖行速度：v===2m/s，‎ ‎∵P===Fv=fv，∴水对钢沉井的阻力f===2.5×106N；‎ ‎（3）设每一个方形孔的面积为S，‎ 钢沉井自行滑入江中稳定后，第一次钢沉井平衡时，F浮=G钢井，且F浮=ρ水gV排，‎ 所以：ρ水g（S整﹣18S）h=mg，‎ ‎1.0×103kg/m3 ×10N/kg×（77m×40m﹣18S）×7.5m=6225×103kg×10N/kg，‎ 解得：S=125m2；‎ 钢板在钢沉井底部将一些方形孔密封起来，设密封的孔有n个，则未堵住的孔有18-n 个。‎ 第二次平衡时，F浮′=G钢井+G板，‎ 即：ρ水g（S整﹣S未堵）h′=mg+m板g，‎ ‎1.0×103kg/m3 ×10N/kg×[77m×40m﹣（18﹣n）×125m2]×3.2m=（6225+31）×103kg×10N/kg，‎ 解得：n=9．‎ 故答案为：（1）惯性；减小摩擦；‎ ‎（2）江水对钢沉井的阻力为2.5×106N；‎ ‎（3）钢沉井底部被密封的方形孔的个数为9个．‎ 第3问另解： ‎ ‎5、（2015黄石）2014年10月为黄石市“中小学科技体育艺术月”，某中学九年级兴趣小组进行了三项物理实践，请根据所给的条件进行计算。‎ ‎（1）小红同学想估测自己站立时对地面的压强。她双脚站立在一张方格纸上，整个脚印范围都与纸面接触，其中一只鞋底的轮廓如图甲所示，已知图中方格的边长为2cm，小红同学的质量为40kg，g取10N/kg。请估算小红同学站立时对地面的压强。‎ ‎（2）小明同学想测量自己快速上楼时克服重力做功的功率。他快速的从一楼跑到五楼，共用时21s，已知小明同学的质量为50kg，每层楼高为3cm，g取9.8N/kg。请计算小明同学快速上楼过程中克服重力做功的功率。‎ ‎（3）大鹏同学想研究浮力问题。如图乙，一支粗细均匀的圆柱体蜡烛，长度L为17cm，底部粘有小石块，将它竖直放入水中静止，露出水面的长度h为1cm，现点燃蜡烛。问：蜡烛是否能够烧完，若能请说明理由；若不能，请求出最后剩余的长度。‎ ‎（已知：ρ蜡=0.9×103kg/m3，ρ水=1.0×103kg/m3）‎ ‎【解析】‎ ‎（1）由图可知，一只脚印所占格数为34格，每小格的面积为2cm×2cm=4cm2=4×10﹣4m2，‎ 双脚接触地面的总面积S=2×34×4×10﹣4m2=2.72×10﹣2m2，‎ G=mg=40kg×10N/kg=400N，‎ 站立时对地面的压力等于其重力F=G=400N，‎ 对地面的压强p==≈1.47×104Pa，‎ ‎（2）小明同学的重力G=mg=50kg×9.8N/kg=490N，‎ 上升高度为h=4×3m=12m，‎ W=Gh=490N×12m=5880J，‎ 克服重力做功的功率P===280W，‎ ‎（3）设小石块重力为G石，体积为V，蜡烛的横截面积为S，‎ 刚点燃时蜡烛整体处于漂浮状态，所以F浮= G蜡+G石，‎ 即ρ水g S（L﹣h）+ρ水gV=ρ蜡g SL +G石 ①‎ 设蜡烛熄灭时，最后剩余的长度为x，此时悬浮，所以F浮′= G蜡′+G石 即ρ水g Sx+ρ水gV=ρ蜡g Sx +G石 ②‎ ‎①- ②得ρ水g S（L﹣h﹣x）=ρ蜡g S（L﹣x） ③，‎ 代入数据解得x=0.07m=7cm．‎ 答：（1）小红同学站立时对地面的压强为1.47×104Pa．‎ ‎（2）上楼过程中克服重力做功的功率为280W；‎ ‎（3）最后剩余的长度为7cm．‎ ‎6、（2015荆门）如图是公厕里间歇式自动冲水箱的原理图，进水管口以Q1=200cm3/s的流量24h不间断地向底面积为1800cm2的长方体水箱注水，当水位上升至h2=45cm时，水箱中的水开始以Q2=2000cm3/s的平均流量从出水管口流出冲洗厕所，当水位下降至h1=5cm处时停止冲水．（不计中水箱中水管的体积）求： （1）水位在h2时水箱底部受到水的压强。 （2）冲洗一次厕所所用的时间。 （3）为节约用水，在图示进水管A处安装一个由微电脑控制的电磁阀。当有人进入洗手间时，门内侧红外探头通过微电脑开启电磁阀，向水箱注水，当水位升至h2时，电磁阀自动关闭停止注水，同时开始冲洗厕所。假设电磁阀平均每天开启100次，则安装电磁阀后一天可节约多少千克水？‎ ‎【解析】‎ ‎（1）h2=45cm=0.45m，‎ 则水箱底部受到水的压强p=ρ水gh2=1.0×103kg/m3×10N/kg×0.45m=4500Pa；‎ ‎（2）当水位从h1上升至h2需要注入的水的体积：‎ V=S△h=S（h2﹣h1）=1800cm2×（45cm﹣5cm）=72000cm3；‎ 冲洗一次厕所所用的时间：‎ t===40s．‎ ‎（3）安装电磁阀前，一天消耗水的体积：‎ V1=Q1t′=200cm3/s×24×3600s=1.728×107cm3=17.28m3‎ 安装电磁阀后，一天消耗水的体积（开启100次）：‎ V2= 100V=100×72000cm3=7.2×106cm3=7.2 m3‎ 则节约的水△V=V1﹣V2=17.28m3﹣7.2m3=10.08m3．‎ 安装电磁阀后，一天节约水的质量：△m=ρ△V=1.0×103kg/m3×10.08m3=1.008×104kg．‎ 答：（1）水位在h2时水箱底部受到水的压强为4500Pa．‎ ‎（2）冲洗一次厕所所用的时间为40s．‎ ‎（3）安装电磁阀后一天可节约1.008×104kg的水．‎ ‎7、（2015孝感）如下图所示，是一辆汽车通过滑轮组将深井中的物体拉至井口的装置图。已知井深12m，物体重G=6×103N，汽车重G车=3×104N，汽车匀速拉绳子时的拉力F= 2.2×103N，汽车受到的阻力为车重的0.1倍。求：‎ ‎（1）将物体从井底拉至井口的过程中，汽车拉绳子的拉力对滑轮组做了多少功？‎ ‎（2）滑轮组的机械效率为多少？（保留一位小数）‎ ‎（3）若汽车运动的速度为3m/s，则将物体由井底拉至井口需要多长时间？‎ ‎（4）汽车牵引力为多少？牵引力的功率为多少？‎ ‎【解析】‎ ‎（1）n=3，s=3h=3×12m=36m，‎ 汽车拉绳子的拉力对滑轮组做的功：W=Fs=2.2×103N×36m=7.92×104J；‎ ‎（2）滑轮组的机械效率：‎ η=×100%=×100%=×100%=×100%=×100%≈90.9%；‎ ‎（3）v物=v=×3m/s=1m/s，‎ 由v=s/t得，将物体由井底拉至井口需要的时间：t物===12s；‎ ‎（4）牵引力：F牵=F′+f=F′+0.1G车=2.2×103N+0.1×3×104N=5.2×103N，‎ 拉力做功功率：P== =F牵v汽=5.2×103N×3 m/s=1.56×104W．‎ 答：（1）汽车拉绳子的拉力对滑轮组做了7.92×104J的功；‎ ‎（2）滑轮组的机械效率为90.9%；‎ ‎（3）若汽车运动的速度为3m/s，则将物体由井底拉至井口需要12s；‎ ‎（4）汽车牵引力为5.2×103N，牵引力的功率为1.56×104W．‎ ‎8、（2015咸宁）一个圆柱形容器放在水平桌面上，如图甲所示，容器中立放着一个均匀实心圆柱体M。现慢慢向容器中加水，加入的水对容器底的压强p水与所加水的质量m的关系如图丙所示，在整个过程中无水溢出，M的底面始终与容器中的水面平行。当加入的水等于3kg时，物体M刚好漂浮且露出水面的高度为4cm，如图乙所示（已知 ρ水=1.0×10kg/m3）。求：‎ ‎（1）圆柱体M刚好漂浮时容器中水的深度h；‎ ‎（2）圆柱体M的密度ρ；‎ ‎（3）圆柱形容器的内底面积S。‎ ‎　【解析】‎ ‎（1）当加入的水m水=3kg时，p水=0.6×103Pa，‎ 由p=ρgh可得，水的深度h= = =0.06m=6cm ‎（2）由于物体M刚好漂浮且露出水面的高度为4cm，‎ 则物体M的高度H=h+h露=6cm+4cm=10cm；‎ 由漂浮条件可知：F浮=G，‎ 即：ρ水V排g=ρ物V物g，‎ 则ρ水Sh浸g=ρ物SHg，‎ 所以ρ物= ρ水 = ×1×103 kg/m3=0.6×103 kg/m3；‎ ‎（3）由于加入的水等于7kg与3kg时压强分别为1.0×103Pa、0.6×103Pa，‎ 由p==得：‎ ‎∴S= = = =0.1m2．‎ ‎　‎ ‎9、（2015随州）一根粗细均匀，长度为1m的木棒AB，将其浸没在水中，并使其可绕B端的水平轴自由转动．为使A端不上浮且维持木棒AB始终水平静止．在A端对其施加一个（方向待求的）力FA=25N，已知木棒重G=100N，木棒的密度和水的密度关系为：‎ ρ木=0.8ρ水，ρ水=1×103kg/m3．求：‎ ‎（1）木棒所受浮力的大小；‎ ‎ （2）力FA的力臂大小；‎ ‎ （3）力FA的可能方向（推导后将相关角度标在图中）‎ ‎【解析】‎ ‎（1）木棒的质量m===10kg，已知ρ木=0.8ρ水=0.8×1×103kg/m3=0.8×103kg/m3，‎ 由ρ=得：木棒的体积V===0.0125m3，‎ 由于木棒AB浸没在水中，则V排=V=0.0125m3，‎ 所以所受浮力F浮=ρ水gV排=V=1×103kg/m3×10N/kg×0.0125m3=125N；‎ ‎（2）由于木棒AB浸没在水中，木棒受浮力和重力的作用，F浮＞G，‎ 则浮力与重力的合力为F=F浮﹣G=125N﹣100N=25N；作用点在重心，方向是：竖直向上；‎ 木棒AB始终水平静止，根据杠杆平衡条件得：FA×=F×L2，‎ 即FA×L1=F×AB，‎ 所以，L1===0.5m；‎ ‎（3）由于使A端不上浮且维持木棒AB始终水平静止，所以在杠杆A端施加阻碍木棒向上转动，则力的方向是向下，由于L1=0.5m；而AB=1m，‎ 所以力FA的可能方向是与AB成30°的角方向是向右下方．‎ 如图：‎ 答：（1）木棒所受浮力的大小为125N；‎ ‎（2）力FA的力臂大小为0.5m；‎ ‎（3）力FA的可能方向是与AB成30°的角，方向是向右下方，如上图．‎ ‎10、（2015黄冈）电动蛙式打夯机（图甲）是利用冲击和冲击振动来夯实、平整场地的机械，由电动机、皮带轮、偏心块、夯架、夯锤等组成（图乙）。启动电动机，在旋转着的偏心块离心力作用下，夯架绕后轴上下摆动，当夯架向下摆动时夯锤就夯击土层，向上摆动时使打夯机前移，故每夯击一次，机身即向前移动一次。右表是某型号电动蛙式打夯机的部分参数（设夯锤夯击土层的能量全部用于夯实土层）。 ‎ ‎（1）若打夯机以10m/min 的平均速度沿直线前进，则10min 前进了多少米？‎ ‎（2）为了估算某次夯锤夯击土层时的冲击力，小明将重为4N、底面积为1cm2的圆柱体竖直平放在被夯击土层上，土层被压下的深度与夯锤夯击的深度相同，则此次夯击时的平均冲击力为多少牛？‎ ‎（3）施工时，若打夯机前移消耗的能量为200J/次，则打夯机的机械效率是多少？‎ ‎【解析】‎ ‎（1）前进的距离s=vt=10m/min×10min=100m；‎ ‎（2）夯锤夯击时对土层的压强；‎ 由题意知，夯锤夯击时对土层的压强等于圆柱体对土层的压强，‎ 故夯击时的平均冲击力F′=pS′=4×104Pa×6×10﹣2=2.4×103N，‎ ‎（3）打夯机工作1min时的有用功W有用=（400+200）J/次×120次=7.2×104J，‎ 由P=可得，W总=W电=Pt=3000W×60s=1.8×105J，‎ 机械效率 答：（1）10min前进了100m；‎ ‎（2）此次夯击时的平均冲击力为2.4×103N，‎ ‎（3）施工时，若打夯机前移消耗的能量为200J/次，则打夯机的机械效率是40%．‎ ‎11、（2015鄂州）为了模拟水中物体被打捞的情境，同学们课外作如下探究：如图，用滑轮组将重200N的物体从底面积为400cm2的圆柱形容器中提起，容器中水面由90cm降到70cm。已知每个滑轮重均为20N（不计绳重、水的阻力及滑轮与中心轴间的摩擦）。‎ 求：（1）所提起物体的密度；‎ ‎ （2）物体完全出水后继续上升的过程中，滑轮组的机械效率。‎ ‎【解析】‎ ‎（1）物体的质量m===20kg=2×104g ‎ ‎ 物体的体积 V=Sh=400×(90-70)cm3=8000cm3‎ ‎ 物体的密度 ρ= ==2.5g/cm3 =2.5×103 kg/m3 ‎ ‎ ‎ 答：所提升物体的密度为2.5×103 kg/m3；滑轮组的机械效率为 90.9％ .‎ ‎12、（2015怀化）如图甲所示，水平桌面上放置底面积为100 cm2、质量为500 g的圆筒，筒内装有20 cm深的某液体。弹簧测力计下悬挂底面积60 cm2、高为10cm的圆柱体，从液面逐渐浸入直至完全浸没，弹簧测力计示数F随圆柱体浸入液体的深度h的变化关系如图乙所示（可以忽略圆筒的厚度，过程中液体始终没有从筒中溢出），g取10N/kg，求：‎ ‎（1）圆柱体完全浸没时受到液体的浮力是多少？‎ ‎（2）筒内液体的密度是多少？‎ ‎（3）当圆柱体完全浸没时，圆筒对桌面的压强是多少？‎ ‎【解析】‎ ‎（1）由图象知，当h=0时，此时测力计的示数等于圆柱体的重力，所以G=18N；‎ 当h≥10cm时，测力计的示数不变，说明此时浮力不变，圆柱体完全浸没，此时F=13.2N；‎ 所以F浮=G﹣F=18N﹣13.2N=4.8N；‎ ‎（2）物体排开液体的体积V排=V物=60×10×10﹣6m3=6×10﹣4m3‎ 由F浮=ρ液gV排得：‎ ρ液===0.8×103kg/m3‎ ‎（3）液体的质量m液=ρ液V液=0.8×103kg/m3×100×20×10﹣6m3=1.6kg 将圆柱体、圆筒、液体看做一个整体，则其对地面的压力：‎ F′=（m液+m筒）g+G物﹣F拉=（1.6kg+0.5kg）×10N/kg+18N﹣13.2N=25.8N 圆筒对桌面的压强：p== =2.58×103Pa．‎ ‎13、（2015仙桃）如图所示，不计外壁厚度且足够高的柱形容器置于水平桌面上，容器的底面积为150cm2．现将一边长为0.1m、质地均匀的正方体物块放在容器底部，当缓慢持续地向容器中注入400cm3的水时，物块对容器底部的压力恰好为零。求：‎ ‎（1）水对容器底部的压强是多少？‎ ‎（2）物块受到水的浮力是多少？‎ ‎（3）再次向容器中缓慢注水，当容器中水的深度达到12cm时停止注水，第二次注入水的质量是多少？‎ ‎　【解析】‎ ‎（1）正方体物块的底面积为S1=10cm×10cm=100 cm2‎ 容器中水的深度是h===8cm 水对容器底部的压强是p=ρ水gh=1.0×103kg/m3×10N/kg×0.08m=8×102Pa；‎ ‎（2）物块排开水的体积V排=S1 h=100cm2×8cm=800cm3‎ 物块受到水的浮力F浮=ρ水V排g=1.0×103kg/m3×10N/kg×8×10﹣4m3=8N ‎ ‎（3）再次注入水的体积V水=S容（h1﹣h）=150cm2×（12cm﹣8cm）=600cm3‎ 再次注入水的质量m=ρ水V水=1.0×103kg/m3×600×10﹣6m3=0.6 kg．‎ 答：（1）水对容器底部的压强是=8×102Pa；‎ ‎（2）物块受到水的浮力是8N；‎ ‎（3）再次向容器中缓慢注水，当容器中水的深度达到12cm时停止注水，第二次注入水的质量是0.6kg．‎ ‎14、（2015包头）有一质量m=0.1kg，容积V＝1×10-3m3，横截面积S＝2.5×10-3m2的圆筒形薄壁容器B（壁厚忽略不计），现注入体积为V的某种液体A后，将其封闭放入水中，且保持竖直漂浮状态，如图9甲所示，此时水对容器底部的压强p＝2.8×103Pa，（容器B内空气质量不计，g取10N/kg）求：‎ ‎ ⑴ 液体A的密度；‎ ‎⑵ 若要使容器B恰好竖直悬浮在水中（如图9乙所示）注入液体A的体积是多少？‎ ‎【解析】‎ ‎（1）F浮＝F向上＝P向上S＝2.8×103pa×2.5×10-3m2＝7N ‎∵整体漂浮 ∴G总=F浮=7N m总=‎ ‎ 液体的质量 m液＝m总－m容＝0.7kg－0.1kg＝0.6kg ‎ ∴液体密度 ρA＝＝=1.8×103kg/m3‎ ‎（2）F浮′ =ρ水gV排=1×103 kg/m3×10N/kg×1×10-3m3=10N ‎∵整体悬浮 ∴G总′=F浮′=10N m总′=‎ ‎ 此时液体的质量 m液′＝m总′－m容＝1kg－0.1kg＝0.9kg ‎ V液′= m液′/ρ液=0.9kg÷1.8×103 kg/m3=5×10-4m3‎ 故答案为 （1）1.8×103kg/m3 （2）5×10－4m3‎ ‎15、（2015宁夏）在青铜峡市“中华黄河坛”文化长廊中，有一尊高大的人物雕像栩栩如生，如图14所示。这引起了小华的兴趣，他想测算雕像的质量以及它对莲花底座的压强有多大。为此，小华从黄河坛文化馆获取了以下的资料：①一枚用同样材质的做成的按比例缩小的雕像样品；②雕像的实际高度H；③从数学知识角度获知，雕像与样品的体积比等于它们高度比的立方。在此基础上，小华又找到了天平、刻度尺、一个能够放入雕像样品的大号量筒、细线、清水等器材进行测算。‎ ‎（1）要测算雕像的质量M ‎，你认为小华至少需要进行哪些操作测量，并用字母表示这些测量的物理量； ‎ ‎（2）请你用已知量、测得量，推导出测算雕像质量M的表达式。 ‎ ‎（3）若莲花底座的受力面积为S，请你写出雕像对莲花底座压强的表达式。‎ ‎ p=  （用已知量、测得量表示）‎ ‎【解析】‎ ‎（1）样品的密度等于雕像的密度，根据m=ρV可知，ρ相同时，质量与体积成正比；‎ 即，而根据题意可知雕像与样品的体积比等于它们高度比的立方，‎ ‎∴= ，H是已知的。‎ 故要测雕像质量的操作是：‎ ‎①用天平测出雕像样品的质量m；‎ ‎②用刻度尺测出样品的高度h；‎ ‎（2）设样品的体积为V0，‎ 由题知，雕像与样品的体积比等于它们高度比的立方，‎ 已知雕像的高度H，已经测出雕像样品的高度h，‎ 则有：=，‎ 所以雕像体积：V雕像=×V0‎ 雕像质量：M=ρV雕像=××V0=．‎ ‎（3）莲花底座的受力面积为S，‎ 雕像对莲花底座压强：p====．‎ 答：（1）测雕像质量的操作：‎ ‎①用天平测出雕像样品的质量m；‎ ‎②用刻度尺测出样品的高度h；‎ ‎（2）雕像质量的表达式M=；‎ ‎（3）．‎ ‎16、（2015青海）如图24所示，小明用滑轮组将重为500N的物体在l0s内匀速提升了1.5m。每个滑轮的重相等，均为20N，不计绳重及摩擦。求：‎ ‎（1）小明受到地面的摩擦力。‎ ‎（2）小明做功的功率。‎ ‎（3）滑轮组的机械效率。‎ ‎【解析】‎ ‎（1）以下面动滑轮为研究对象，∴‎ 以上面动滑轮为研究对象，受向下的重力、向下的绳子拉力F1和向上的2段绳子拉力2F2 。‎ ‎∵匀速提升物体，∴ ，即20N+260N=2F2.‎ 解得F2=140N.‎ ‎∵小明受向左的绳子拉力F2和地面的摩擦力f而处于静止状态，‎ ‎∴f=F2=140N .‎ ‎（2）物体提升高度为h，则上面的动滑轮提升的高度为2h 。‎ 以上面动滑轮为研究对象，则绳子自由端移动的距离s=2×2h=4×1.5m=6m。‎ 小明做功的功率 ‎（3）滑轮组的机械效率 答：（1）小明受到地面的摩擦力为140N； （2）小明做功的功率为84W； （3）滑轮组的机械效率为89.29% 。‎ ‎17、（2015乌鲁木齐）如图，将含有一空心铝球的冰块投入平底水槽中，冰块内空心铝球的体积V铝=10cm3，当冰块（含空心铝球）悬浮时，排开水的体积V排=45cm3．冰全部熔化后，浸没在水中的空心铝球沉入水底，已知冰的密度ρ冰=0.9×103kg/m3，求：‎ ‎（1）冰块（含空心铝球）在水中悬浮时的重力；‎ ‎（2）空心铝球最终对水槽底部的压力大小．‎ ‎【解析】‎ ‎（1）冰块（含空心铝球）完全浸没时受到的浮力：‎ F浮=ρ水gV排=1.0×103kg/m3×10N/kg×45×10﹣6m3=0.45N；‎ 由于冰块（含空心铝球）处于悬浮，则冰块（含空心铝球）重力G=F浮=0.45N；‎ ‎（2）冰的体积V=V排﹣V铝=45cm3﹣10cm3=35cm3=35×10﹣6m3，‎ 由ρ=和G=mg得冰的重力：‎ G=mg=ρ冰Vg=0.9×103kg/m3×10N/kg×35×10﹣6m3=0.315N；‎ 空心铝球的重力：G球=G﹣G冰=0.45N﹣0.315N=0.135N；‎ 由于空心铝球沉在底部，则受到的浮力：‎ F浮=ρ水gV排=ρ水gV铝=1.0×103kg/m3×10N/kg×10×10﹣6m3=0.1N；‎ 对水槽底部的压力：F=G﹣F浮=0.135N﹣0.1N=0.035N．‎ 答：（1）冰块（含空心铝球）在水中悬浮时的重力为0.45N；‎ ‎（2）空心铝球最终对水槽底部的压力大小为0.035N．‎