中考数学压轴题一及解答 26页

2010 年中考数学压轴题（一）及解答 1、（2010 年北京市）24. 在平面直角坐标系 xOy 中，抛物线 y= − x2+ x+m2−3m+2 与 x 轴的交点分别为原点 O 和点 A，点 B(2，n)在这条抛物线上。 (1) 求点 B 的坐标； (2) 点 P 在线段 OA 上，从 O 点出发向点运动，过 P 点作 x 轴的 垂线，与直线 OB 交于点 E。延长 PE 到点 D。使得 ED=PE。 以 PD 为斜边在 PD 右侧作等腰直角三角形 PCD(当 P 点运动 时，C 点、D 点也随之运动)  当等腰直角三角形 PCD 的顶点 C 落在此抛物线上时，求 OP 的长；  若 P 点从 O 点出发向 A 点作匀速运动，速度为每秒 1 个单位，同时线段 OA 上另一 点 Q 从 A 点出发向 O 点作匀速运动，速度为每秒 2 个单位(当 Q 点到达 O 点时停止 运动，P 点也同时停止运动)。过 Q 点作 x 轴的垂线，与直线 AB 交于点 F。延长 QF 到点 M，使得 FM=QF，以 QM 为斜边，在 QM 的左侧作等腰直角三角形 QMN(当 Q 点运动时，M 点，N 点也随之运动)。若 P 点运动到 t 秒时，两个等腰直角三角形分 别有一条直角边恰好落在同一条直线上，求此刻 t 的值。 【解答】 24. 解：(1) ∵拋物线 y= − x2+ x+m2−3m+2 经过原点，∴m2−3m+2=0，解得 m1=1，m2=2， 由题意知 m≠1，∴m=2，∴拋物线的解析式为 y= − x2+ x，∵点 B(2，n)在拋物线 y= − x2+ x 上，∴n=4，∴B 点的坐标为(2，4)。 (2)  设直线 OB 的解析式为 y=k1x，求得直线 OB 的解析式为 y=2x，∵A 点是拋物线与 x 轴的一个交点，可求得 A 点的 坐标为(10，0)，设 P 点的坐标为(a，0)，则 E 点的坐标为 (a，2a)，根据题意作等腰直角三角形 PCD，如图 1。可求 得点 C 的坐标为(3a，2a)，由 C 点在拋物线上，得 2a= − ×(3a)2+ ×3a，即 a2− a=0，解得 a1= ，a2=0 (舍去)，∴OP= 。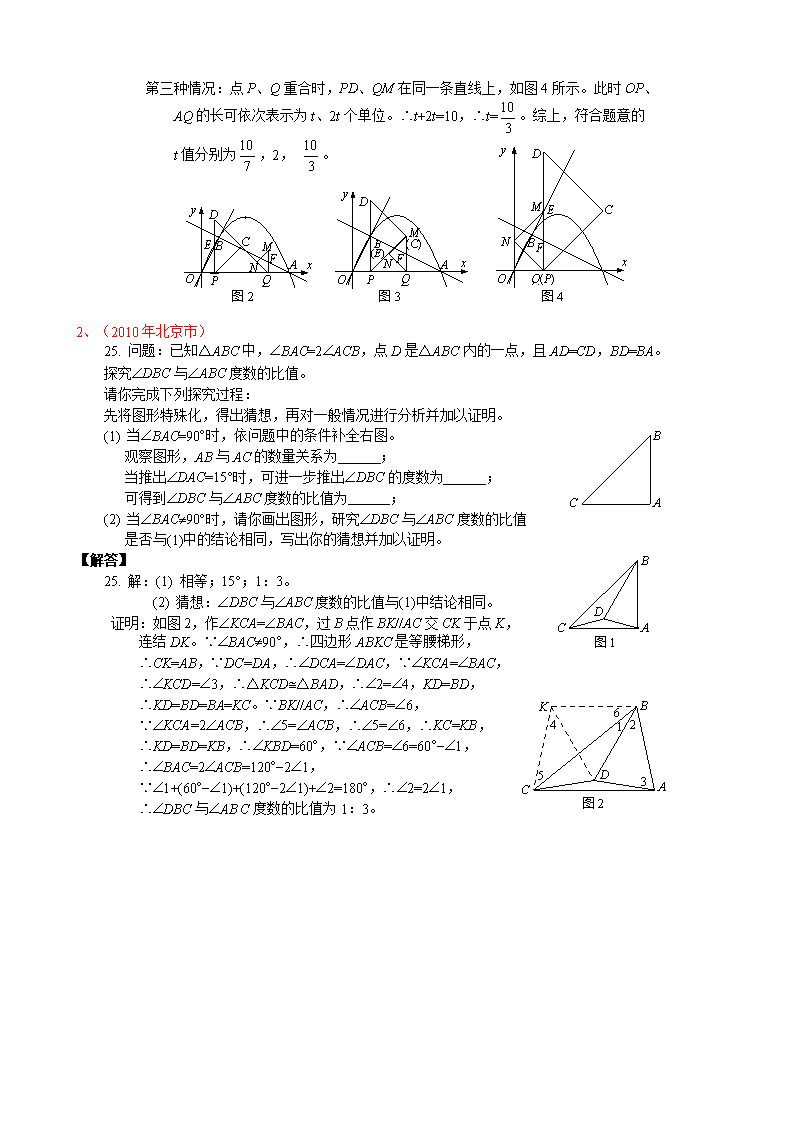  依题意作等腰直角三角形 QMN，设直线 AB 的解析式为 y=k2x+b，由点 A(10，0)， 点 B(2，4)，求得直线 AB 的解析式为 y= − x+5，当 P 点运动到 t 秒时，两个等腰 直角三角形分别有一条边恰好落在同一条直线上，有以下三种情况： 第一种情况：CD 与 NQ 在同一条直线上。如图 2 所示。可证△DPQ 为等腰直角三 角形。此时 OP、DP、AQ 的长可依次表示为 t、4t、2t 个单位。∴PQ=DP=4t， ∴t+4t+2t=10，∴t= 。 第二种情况：PC 与 MN 在同一条直线上。如图 3 所示。可证△PQM 为等腰直角三 角形。此时 OP、AQ 的长可依次表示为 t、2t 个单位。∴OQ=10−2t，∵F 点在 直线 AB 上，∴FQ=t，∴MQ=2t，∴PQ=MQ=CQ=2t，∴t+2t+2t=10，∴t=2。 4 1−m 4 5m 4 1−m 4 5m 4 1 2 5 4 1 2 5 4 1 2 5 4 9 2 11 9 22 9 22 2 1 7 10 x y O 1 1 O A B C D E P y x 图 1 第三种情况：点 P、Q 重合时，PD、QM 在同一条直线上，如图 4 所示。此时 OP、 AQ 的长可依次表示为 t、2t 个单位。∴t+2t=10，∴t= 。综上，符合题意的 t 值分别为 ，2， 。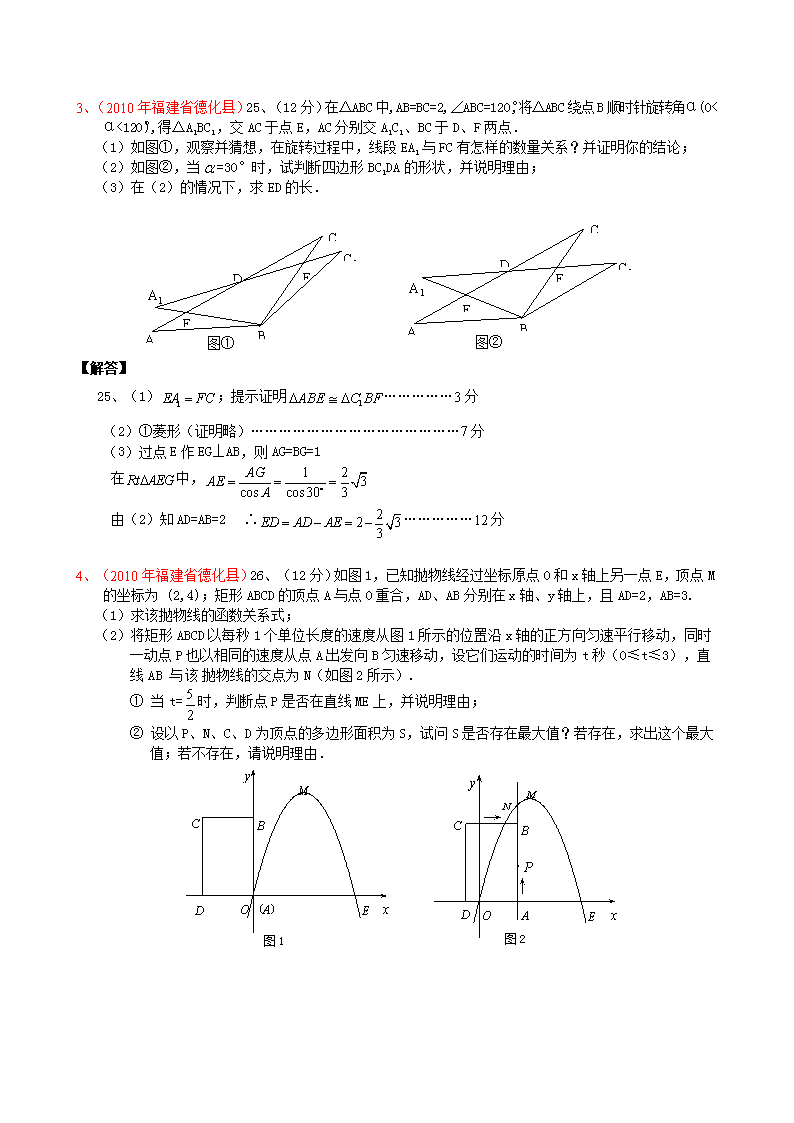 2、（2010 年北京市） 25. 问题：已知△ABC 中，∠BAC=2∠ACB，点 D 是△ABC 内的一点，且 AD=CD，BD=BA。 探究∠DBC 与∠ABC 度数的比值。 请你完成下列探究过程： 先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明。 (1) 当∠BAC=90°时，依问题中的条件补全右图。 观察图形，AB 与 AC 的数量关系为 ； 当推出∠DAC=15°时，可进一步推出∠DBC 的度数为 ； 可得到∠DBC 与∠ABC 度数的比值为 ； (2) 当∠BAC≠90°时，请你画出图形，研究∠DBC 与∠ABC 度数的比值 是否与(1)中的结论相同，写出你的猜想并加以证明。 【解答】 25. 解：(1) 相等；15°；1：3。 (2) 猜想：∠DBC 与∠ABC 度数的比值与(1)中结论相同。 证明：如图 2，作∠KCA=∠BAC，过 B 点作 BK//AC 交 CK 于点 K， 连结 DK。∵∠BAC≠90°，∴四边形 ABKC 是等腰梯形， ∴CK=AB，∵DC=DA，∴∠DCA=∠DAC，∵∠KCA=∠BAC， ∴∠KCD=∠3，∴△KCD≅△BAD，∴∠2=∠4，KD=BD， ∴KD=BD=BA=KC。∵BK//AC，∴∠ACB=∠6， ∵∠KCA=2∠ACB，∴∠5=∠ACB，∴∠5=∠6，∴KC=KB， ∴KD=BD=KB，∴∠KBD=60°，∵∠ACB=∠6=60°−∠1， ∴∠BAC=2∠ACB=120°−2∠1， ∵∠1+(60°−∠1)+(120°−2∠1)+∠2=180°，∴∠2=2∠1， ∴∠DBC 与∠AB C 度数的比值为 1：3。 3 10 7 10 3 10 AC B E x O A B C y P M Q N F D 图 2 x y O A M (C)B (E) D P Q FN 图 3 图 4 y x B O Q(P) N C D M E F D AC B 图 1 B AC D K 1 2 3 4 5 6 图 2 3、（2010 年福建省德化县）25、（12 分）在△ABC 中,AB=BC=2,∠ABC=120°,将△ABC 绕点 B 顺时针旋转角α(0< α<120°),得△A1BC1，交 AC 于点 E，AC 分别交 A1C1、BC 于 D、F 两点． （1）如图①，观察并猜想，在旋转过程中，线段 EA1 与 FC 有怎样的数量关系？并证明你的结论； （2）如图②，当 =30°时，试判断四边形 BC1DA 的形状，并说明理由； （3）在（2）的情况下，求 ED 的长． 【解答】 25、（1） ；提示证明 ……………3 分 （2）①菱形（证明略）………………………………………7 分 （3）过点 E 作 EG⊥AB，则 AG=BG=1 在 中， 由（2）知 AD=AB=2 ∴ ……………12 分 4、（2010 年福建省德化县）26、（12 分）如图 1，已知抛物线经过坐标原点 O 和 x 轴上另一点 E，顶点 M 的坐标为 (2,4)；矩形 ABCD 的顶点 A 与点 O 重合，AD、AB 分别在 x 轴、y 轴上，且 AD=2，AB=3. （1）求该抛物线的函数关系式； （2）将矩形 ABCD 以每秒 1 个单位长度的速度从图 1 所示的位置沿 x 轴的正方向匀速平行移动，同时 一动点 P 也以相同的速度从点 A 出发向 B 匀速移动，设它们运动的时间为 t 秒（0≤t≤3），直 线 AB 与 该 抛物线的交点为 N（如图 2 所示）. ① 当 t= 时，判断点 P 是否在直线 ME 上，并说明理由； ② 设以 P、N、C、D 为顶点的多边形面积为 S，试问 S 是否存在最大值？若存在，求出这个最大 值；若不存在，请说明理由． α 1EA FC= 1ABE C BF∆ ≅ ∆ Rt AEG∆ 1 2 3cos cos30 3 AGAE A = = =  22 33ED AD AE= − = − 2 5 C1 A1 F E D C BA 图① C1 A1 F E D C BA 图② 图 2 BC O AD E M y x P N · 图 1 BC O (A)D E M y x 【解答】 26、解：（1） ……………3 分 （2）①点 P 不在直线 ME 上…………………7 分 ②依题意可知：P（ , ），N（ ， ） 当 时，以 P、N、C、D 为顶点的多边形是四边形 PNCD，依题意可得： = + = + = = ∵抛物线的开口方向：向下，∴当 = ，且 时， = 当 时,点 P、N 都重合，此时以 P、N、C、D 为顶点的多边形是三角形 依题意可得， = =3 综上所述，以 P、N、C、D 为顶点的多边形面积 S 存在最大值 ．………12 分 5、（2010 年福建省福州市）22.（满分 14 分） 如图 1，在平面直角坐标系中，点 B 在直线 上，过点 B 作 轴的垂线，垂足为 A，OA=5。 若抛物线 过点 O、A 两点。 （1）求该抛物线的解析式； （2）若 A 点关于直线 的对称点为 C，判断点 C 是否在该抛物线上，并说明理由； （3）如图 2，在（2）的条件下，⊙O1 是以 BC 为直径的圆。过原点 O 作 O1 的切线 OP，P 为切点（P 与点 C 不重合），抛物线上是否存在点 Q，使得以 PQ 为直径的圆与 O1 相切？若存在，求出点 Q 的横坐标；若不存在，请说明理由。 xxy 42 +−= t t t tt 42 +− 30  t PNCPCD SSS  += ODCD ⋅ 2 1 BCPN ⋅ 2 1 232 1 ×× ( ) 242 1 2 ⋅−+− ttt 332 ++− tt 4 21)2 3( 2 +−− t t 2 3 32 30  =t 最大S 4 21 03或=t ABCDSS 矩形2 1= 322 1 ×× 4 21 2y x= x 21 6y x bx c= + + 2y x= 【解答】 6、（2010 年福建省晋江市）25.（13 分）已知：如图，把矩形 放置于直角坐标系中， ， ，取 的中点 ，连结 ，把 沿 轴的负方向平移 的长度后得到 . (1)试直接写出点 的坐标； (2)已知点 与点 在经过原点的抛物线上，点 在第一象限内的该抛物线上移动，过点 作 轴于点 ，连结 . ①若以 、 、 为顶点的三角形与 相似，试求出点 的坐标； ②试问在抛物线的对称轴上是否存在一点 ，使得 的值最大. OCBA 3=OC 2=BC AB M MC MBC∆ x OC DAO∆ D B D P P xPQ ⊥ Q OP O P Q DAO∆ P T TBTO − A O x B C M y 【解答】 25.（本小题 13 分） 解：(1)依题意得： ；………（3 分） (2) ① ∵ ， ，∴ . ∵抛物线经过原点， ∴设抛物线的解析式为 又抛物线经过点 与点 ∴ 解得： ∴抛物线的解析式为 .…………………（5 分） ∵点 在抛物线上， ∴设点 . 1)若 ∽ ，则 ， ，解得： (舍去)或 ， ∴点 .………………………………………………………………（7 分） 2)若 ∽ ，则 ， ，解得： (舍去)或 ， ∴点 .……………………………………………………………………（9 分） ②存在点 ，使得 的值最大. 抛 物 线 的 对 称 轴 为 直 线 ， 设 抛 物 线 与 轴 的 另 一 个 交 点 为 ， 则 点     − 2,2 3D 3=OC 2=BC ( )2,3B bxaxy += 2 ( )0≠a ( )2,3B     − 2,2 3D    =− =+ 22 3 4 9 ,239 ba ba      −= = 3 2 ,9 4 b a xxy 3 2 9 4 2 −= P      − xxxP 3 2 9 4, 2 PQO∆ DAO∆ AO QO DA PQ = 2 2 3 3 2 9 4 2 xxx = − 01 =x 16 51 2 =x      64 153,16 51P OQP∆ DAO∆ AO PQ DA OQ = 2 3 2 9 4 2 3 2 xxx − = 01 =x 2 9 2 =x      6,2 9P T TO TB− xxy 3 2 9 4 2 −= 4 3=x x E A O x D B C M y E P T Q .………………………………………………………………………（10 分） ∵点 、点 关于直线 对称， ∴ ……………………………………………………………………（11 分） 要使得 的值最大，即是使得 的值最大， 根 据 三 角 形 两 边 之 差 小 于 第 三 边 可 知 ， 当 、 、 三 点 在 同 一 直 线 上 时 ， 的 值 最 大. ……………………………………………………………………………（12 分） 设过 、 两点的直线解析式为 ， ∴ 解得： ∴直线 的解析式为 . 当 时， . ∴存在一点 使得 最大.………………………（13 分） 7、（2010 年福建省晋江市）26.（13 分）如图，在等边 中，线段 为 边上的中线. 动点 在直线 上时，以 为一边且在 的下方作等边 ，连结 . (1) 填空： 度； (2) 当点 在线段 上(点 不运动到点 )时，试求出 的值； (3)若 ，以点 为圆心，以 5 为半径作⊙ 与直线 相交于点 、 两点，在点 运动的过 程中(点 与点 重合除外)，试求 的长.      0,2 3E O E 4 3=x TETO = TBTO − TBTE − T E B TBTE − B E bkxy += ( )0≠k    =+ =+ 02 3 ,23 bk bk    −= = 2 ,3 4 b k BE 23 4 −= xy 4 3=x 124 3 3 4 −=−×=y      −1,4 3T TO TB− ABC∆ AM BC D AM CD CD CDE∆ BE ______ACB∠ = D AM D A BE AD 8=AB C C BE P Q D D A PQ E B M A C D A B C 备用图(1) A B C 备用图(2) 【解答】 26.（本小题 13 分） (1)60；…………………………………………（3 分） (2)∵ 与 都是等边三角形 ∴ ， ， ∴ ∴ ……………………………（5 分） ∴ ≌ ∴ ，∴ .………………………（7 分） (3) ①当点 在线段 上（不与点 重合）时，由(2) 可知 ≌ ，则 ，作 于点 ，则 ，连结 ，则 . 在 中 ， ， ， 则 . 在 中，由勾股定理得： ，则 .………………………（9 分） ② 当 点 在 线 段 的 延 长 线 上 时 ， ∵ 与 都是等边三角形 ∴ ， ， ∴ ∴ ∴ ≌ ∴ ，同理可得： .…………………………（11 分） ③当点 在线段 的延长线上时， ∵ 与 都是等边三角形 ∴ ， ， ∴ ∴ ∴ ≌ ∴ ∵ ∴ ∴ . ABC∆ DEC∆ BCAC = CECD = °=∠=∠ 60DCEACB BCEDCBDCBACD ∠+∠=∠+∠ BCEACD ∠=∠ ACD∆ BCE∆ ( )SAS BEAD = 1= BE AD D AM A ACD∆ BCE∆ °=∠=∠ 30CADCBE BECH ⊥ H HQPQ 2= CQ 5=CQ CBHRt∆ °=∠ 30CBH 8== ABBC 42 1830sin =×=°⋅= BCCH CHQRt∆ 345 2222 =−=−= CHCQHQ 62 == HQPQ D AM ABC∆ DEC∆ BCAC = CECD = °=∠=∠ 60DCEACB DCEDCBDCBACB ∠+∠=∠+∠ BCEACD ∠=∠ ACD∆ BCE∆ ( )SAS °=∠=∠ 30CADCBE 6=PQ D MA ABC∆ DEC∆ BCAC = CECD = °=∠=∠ 60DCEACB °=∠+∠=∠+∠ 60ACEBCEACEACD BCEACD ∠=∠ ACD∆ BCE∆ ( )SAS CADCBE ∠=∠ °=∠ 30CAM °=∠=∠ 150CADCBE °=∠ 30CBQ P Q E B M A D C P Q E B M A D C H Q P E B M A D C 同理可得： . 综上， 的长是 6. ………………………（13 分） 8、（2010 年福建省龙岩市）24.（13 分） 在平面直角坐标系中，点 A、B 的坐标分别为（ 10，0），（2，4）. （1）若点 C 是点 B 关于 x 轴的对称点，求经过 O、C、A 三点的抛物线的解析式； （2）若 P 为抛物线上异于 C 的点，且△OAP 是直角三角形，请直接写出点 P 的坐标； （3）若抛物线顶点为 D，对称轴交 x 轴于点 M,探究：抛物线对称轴上是否存在异于 D 的 点 Q，使△AQD 是等腰三角形，若存在，请求出点 Q 的坐标；若不存在，请说明理由. 【解答】 则结合图形，可求得满足条件的 Q 点坐标为(5, )，(5, ) 记为 Q2(5, ),Q3(5, )； …………11 分 若 则设 Q（5,y），由 解得 y= , 所以满足条件的 Q 点坐标为（5， ），记为 Q4(5, )…12 分 所以，满足条件的点 Q 有 Q1(5, ), , , ……13 分 6=PQ PQ 5 41 25 4 − 5 41 25 4 +− 5 41 25 4 − 5 41 25 4 +− QD QA= 225 25 4 y y+ = + 252 8 − 252 8 − 252 8 − 25 4 2 5 41-25Q (5, )4 3 5 41+25Q (5,- )4 4 25Q (5,2- )8 9、（2010 年福建省龙岩市）25.（14 分） 如图，将含 30°角的直角三角板 ABC（∠A=30°）绕其直角顶点 C 逆时针旋转 角（ ）， 得到 Rt△ ， 与 AB 交于点 D，过点 D 作 DE∥ 交 于 点 E，连结 BE.易知，在 旋转过程中，△BDE 为直角三角形. 设 BC=1，AD=x，△BDE 的 面积为 S. （1）当 时，求 x 的值. （2）求 S 与 x 的函数关系式，并写出 x 的取值范围； （3）以点 E 为圆心，BE 为半径作⊙E，当 S= 时，判断⊙E 与 的位置关 系，并求相应的 值. 【解答】 过 D 作 于 ，则 ， α 0 90α° < < ° ' 'A B C 'A C ' 'A B 'CB 30α = ° 1 4 ABCS∆ 'A C tanα DF AC⊥ F 1 1 2 4DF x= = 33 4AF DF= = ∴ ∴ . ………12 分 ② 当 时 ， ， ∴ ∴ ∴此时 与 相交. ……13 分 同理可求出 . ………14 分 10、(2010 年福建省南安市)25．(13 分) 某公园有一个抛物线形状的观景拱桥 ABC，其横截面如图所示， 在图中建立的直角坐标系中，抛物线的解析式为 且过顶点 C（0，5）（长度单位：m） （1）直接写出 c 的值； （2）现因搞庆典活动，计划沿拱桥的台阶表面铺设一条宽度为 1.5 m 的地毯，地毯的价格为 20 元 / , 求购买地毯需多少元？ （3）在拱桥加固维修时，搭建的“脚手架”为矩形 EFGH（H、G 分别在抛物线的左右侧上），并铺设斜面 EG.已知矩形 EFGH 的周长为 27.5 m，求斜面 EG 的倾斜角∠GEF 的度数.（精确到 0.1°） 【解答】 25．（本小题 13 分） 解(1)c=5．……………………………3 分 （2）由（1）知，OC=5，…………………………4 分 令 ，即 ，解得 ．…………5 分 ∴地毯的总长度为： ，………………6 分 ∴ （元）． 答：购买地毯需要 900 元．……………………7 分 (3)可设 G 的坐标为 ,其中 ， 则 ． ………………………………………8 分 由已知得： ， 即 ，………………………………………9 分 解得： （不合题意，舍去）．………………………10 分 3 33 34 4CF = − = 3tan 9 DF CF α = =3 2x = 3 12 2 2BD = − = 3 2BE = 2 2 1DE BD BE= + = 1 1 2 2EC DE BE= = < E A C′ 3 4tan 31 34 α = = cxy +−= 2 20 1 2m 0=y 0520 1 2 =+− x 10,10 21 −== xx 3052202 =×+=+ OCAB 900205.130 =×× )520 1,( 2 +− mm 0>m 520 1,2 2 +−== mGFmEF 5.27)(2 =+ GFEF 5.27)520 12(2 2 =+− mm 35,5 21 == mm 把 代入 ． ∴点 G 的坐标是（5，3.75）．…………………………………… ……11 分 ∴ ． 在 Rt△EFG 中， ，……………12 分 ∴ ．…………………13 分 11 、 （ 2010 年 福 建 省 南 安 市 ） 26. （ 13 分 ） 如 图 1 ， 在 中 ， ， ， ，另有一等腰梯形 （ ）的底边 与 重合，两腰分别落在 AB、AC 上，且 G、F 分别是 AB、AC 的中点． （1）直接写出△AGF 与△ABC 的面积的比值； （2）操作：固定 ，将等腰梯形 以每秒 1 个单位的速度沿 方向向右运动，直到点 与点 重合时停止．设运动时间为 秒，运动后的等腰梯形为 （如图 2）． ①探究 1：在运动过程中，四边形 能否是菱形？若能，请求出此时 的值；若不能，请说 明理由． ②探究 2：设在运动过程中 与等腰梯形 重叠部分的面积为 ，求 与 的函数关 系式． 【解答】 26．（本小题 13 分） 解：（1）△AGF 与△ABC 的面积比是 1：４．………………………3 分 （2）①能为菱形．……………………4 分 由于 FC∥ ，CE∥ ， 四边形 是平行四边形．…………………………5 分 当 时，四边形 为菱形，………………… 6 分 此时可求得 ． 当 秒时，四边形 为………… 7 分 ②分两种情况： ①当 时， 如图 3 过点 作 于 ． Rt ABC△ 90A∠ =  AB AC= 4 2BC = DEFG GF DE∥ DE BC ABC△ DEFG BC D C x DEF G′ ′ x ABC△ DEFG y y x ∴ 2x = ∴ 2x = 0 2 2x <≤ G GM BC⊥ M 51 =m 520 1 2 +− m 75.35520 1 2 =+×−= 75.3,10 == GFEF 375.010 75.3tan ===∠ EF GFGEF 06.20≈∠GEF FFCE ′ FE ′ FF ′ FFCE ′ 22 1 === ACCFCE FFCE ′ FFCE ′ A FG (D)B C(E) 图 1 FG A F′G′ B D C E 图 2 A FG (D)B C(E) 图 3M ， ， ， 为 中点， ． 又 分别为 的中点， ．…………………… 8 分 方法一： 等腰梯形 的面积为 6． ， ．…………… …………… 9 分 重叠部分的面积为： ． 当 时， 与 的函数关系式为 ．………………10 分 方法二： ， ， ，………… ……… 9 分 重叠部分的面积为： ． 当 时， 与 的函数关系式为 ．………………10 分 ②当 时， 设 与 交于点 ， 则 ． ， ， 作 于 ，则． ……………11 分 重叠部分的面积为： ． 综上，当 时， 与 的函数关系式为 ；当 时， …………………13 分 AB AC= 90BAC∠ =  4 2BC = G AB 2GM∴ = G F ， AB AC， 1 2 22GF BC∴ = = 1 (2 2 4 2) 2 62DEFGS∴ = + × =梯形 ∴ DEFG 2GM = 2BDG GS x′∴ =  ∴ 6 2y x= − ∴ 0 2 2x <≤ y x 6 2y x= − 2 2FG x′ = − 4 2DC x= − 2GM = ∴ (2 2 ) (4 2 ) 2 6 22 x xy x − + −= × = − ∴ 0 2 2x <≤ y x 6 2y x= − 2 2 4 2x≤ ≤ FC DG′ P 45PDC PCD∠ = ∠ =  90CPD∴∠ =  PC PD= PQ DC⊥ Q 1 (4 2 )2PQ DQ QC x= = = − ∴ 2 21 1 1 1(4 2 ) (4 2 ) (4 2 ) 2 2 82 2 4 4y x x x x x= − × − = − = − + 0 2 2x <≤ y x 6 2y x= − 2 2 4 2x≤ ≤ 8224 1 2 +−= xxy FG A F′G′ B C E 图 4 QD P 12、（2010 年福建省南平市）25．（14 分）如图 1，在△ABC 中，AB=BC，P 为 AB 边上一点，连接 CP，以 PA、PC 为邻边作□APCD，AC 与 PD 相交于点 E，已知∠ABC=∠AEP=α（0°<α<90°）. （1）求证：∠EAP=∠EPA； （2）□APCD 是否为矩形？请说明理由； （3）如图 2，F 为 BC 中点，连接 FP，将∠AEP 绕点 E 顺时针旋转适当的角度，得到∠MEN（点 M、N 分别是∠MEN 的两边与 BA、FP 延长线的交点）.猜想线段 EM 与 EN 之间的数量关系，并证明你的结论. 【解答】 25、(1)证明：在 ΔABC 和 ΔAEP 中 ∵∠ABC=∠AEP，∠BAC=∠EAP ∴ ∠ACB=∠APE 在 ΔABC 中，AB=BC ∴∠ACB=∠BAC ∴ ∠EPA=∠EAP (2)答：□ APCD 是矩形 ∵四边形 APCD 是平行四边形 ∴ AC=2EA, PD=2EP ∵ 由（1）知 ∠EPA=∠EAP ∴ EA=EP 则 AC=PD ∴□APCD 是矩形 (3)答： EM=EN ∵EA=EP ∴ ∠EPA=90°－ 1 2α ∴∠EAM=180°-∠EPA=180°-(90°- 1 2α)=90°+ 1 2α 由（2）知∠CPB=90°,F 是 BC 的中点，∴ FP=FB ∴∠FPB=∠ABC=α ∴ ∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°- 1 2α+α=90°+ 1 2α ∴ ∠EAM=∠EPN ∵ ∠AEP 绕点 E 顺时针旋转适当的角度，得到∠MEN ∴ ∠AEP=∠MEN ∴∠AEP- ∠AEN=∠MEN-∠AEN 即 ∠MEA=∠NEP ∴ ΔEAM≌ΔEPN ∴ EM=EN 13、（2010 年福建省南平市）26.(14 分)如图 1，已知点 B（1，3）、C（1，0），直线 y=x+k 经过点 B， 且与 x 轴交于点 A，将△ABC 沿直线 AB 折叠得到△ABD. 图 1 A B D C E P 图 2 A B D C E PM N F （1）填空：A 点坐标为（____，____），D 点坐标为（____，____）； （2）若抛物线 y= 1 3x2+bx+c 经过 C、D 两点，求抛物线的解析式； （3）将（2）中的抛物线沿 y 轴向上平移，设平移后所得抛物线与 y 轴交点为 E，点 M 是平移后的抛物线 与直线 AB 的公共点，在抛物线平移过程中是否存在某一位置使得直线 EM∥x 轴.若存在，此时抛物线向上 平移了几个单位？若不存在，请说明理由. （提示：抛物线 y=ax2+bx+c(a≠0)的对称轴是 x=－ b 2a，顶点坐标是（－ b 2a， 4a c－b2 4a ） 【解答】 26.解：（1） A(-2,0) ,D(-2,3) (2)∵抛物线 y= 1 3x2+bx+c 经过 C(1,0), D(-2,3) 代入，解得：b=- 2 3,c= 1 3 ∴ 所求抛物线解析式为：y= 1 3x2 － 2 3 x+1 3 （3）答：存在 解法一： 设抛物线向上平移 H 个单位能使 EM∥x 轴， 则平移后的解析式为：y= 1 3x2 － 2 3 x+1 3+h = (x -1)² + h 此时抛物线与 y 轴交点 E(0, +h) 当点 M 在直线 y=x+2 上，且满足直线 EM∥x 轴时 则点 M 的坐标为（ ） 又 ∵M 在平移后的抛物线上，则有 +h= (h- -1)²+h 解得： h= 或 h= （і）当 h= 时，点 E（0，2），点 M 的坐标为（0，2）此时，点 E,M 重合，不合题意舍去。 （ii）当 h= 时，E（0，4）点 M 的坐标为（2，4）符合题意 综合（i）（ii）可知，抛物线向上平移 个单位能使 EM∥x 轴。 3 1 3 1 hh +− 3 1,3 5 3 1 3 1 3 5 3 5 3 11 3 5 3 11 3 11 O y xA D B C 图 1 O y xA B C 备用图 · 解法二：∵当点 M 在抛物线对称轴的左侧或在抛物线的顶点时，仅当 M,E 重合时，它们的纵坐标相等。 ∴EM 不会与 x 轴平行 当点 M 在抛物线的右侧时，设抛物线向上平移 H 个单位能使 EM∥x 轴 则平移后的抛物线的解析式为∵y= x² + +h = (x - 1)² + h ∴ 抛物线与 Y 轴交点 E(0, +h) ∵抛物线的对称轴为：x=1 根据抛物线的对称性，可知点 M 的坐标为（2， +h)时，直线 EM∥x 轴 将（2， +h)代入 y=x+2 得， +h=2+2 解得：h= ∴ 抛物线向上平移 个单位能使 EM∥x 轴 14、（2010 年福建省宁德市）25．（本题满分 13 分）如图，四边形 ABCD 是正方形，△ABE 是等边三角形， M 为对角线 BD（不含 B 点）上任意一点，将 BM 绕点 B 逆时针旋转 60°得到 BN，连接 EN、AM、CM. ⑴ 求证：△AMB≌△ENB； ⑵ ①当 M 点在何处时，AM＋CM 的值最小； ②当 M 点在何处时，AM＋BM＋CM 的值最小，并说明理由； ⑶ 当 AM＋BM＋CM 的最小值为 时，求正方形的边长. 【解答】 25．（满分 13 分）解：⑴∵△ABE 是等边三角形， ∴BA＝BE，∠ABE＝60°. ∵∠MBN＝60°， ∴∠MBN－∠ABN＝∠ABE－∠ABN. 即∠BMA＝∠NBE. 又∵MB＝NB， ∴△AMB≌△ENB（SAS）. ………………5 分 ⑵①当 M 点落在 BD 的中点时，AM＋CM 的值最小. ………………7 分 ②如图，连接 CE，当 M 点位于 BD 与 CE 的交点处时， AM＋BM＋CM 的值最小. ………………9 分 理由如下：连接 MN.由⑴知，△AMB≌△ENB， ∴AM＝EN. ∵∠MBN＝60°，MB＝NB， ∴△BMN 是等边三角形. ∴BM＝MN. ∴AM＋BM＋CM＝EN＋MN＋CM. ………………10 分 3 1 x3 2− 3 1 3 1 3 1 3 1 3 1 3 1 3 11 3 11 13 + E A D B C N M F E A D B C N M 根据“两点之间线段最短”，得 EN＋MN＋CM＝EC 最短 ∴当 M 点位于 BD 与 CE 的交点处时，AM＋BM＋CM 的值最小，即等于 EC 的长.……11 分 ⑶过 E 点作 EF⊥BC 交 CB 的延长线于 F， ∴∠EBF＝90°－60°＝30°. 设正方形的边长为 x，则 BF＝ x，EF＝ . 在 Rt△EFC 中， ∵EF2＋FC2＝EC2， ∴（ ）2＋（ x＋x）2＝ . ………………12 分 解得，x＝ （舍去负值）. ∴正方形的边长为 . ………………13 分 15、（2010 年福建省宁德市）26.（本题满分 13 分）如图，在梯形 ABCD 中，AD∥BC，∠B＝90°，BC＝6， AD＝3，∠DCB＝30°.点 E、F 同时从 B 点出发，沿射线 BC 向右匀速移动.已知 F 点移动速度是 E 点移动速 度的 2 倍，以 EF 为一边在 CB 的上方作等边△EFG．设 E 点移动距离为 x（x＞0）. ⑴△EFG 的边长是____（用含有 x 的代数式表示），当 x＝2 时，点 G 的位置在_______； ⑵若△EFG 与梯形 ABCD 重叠部分面积是 y，求 ①当 0＜x≤2 时，y 与 x 之间的函数关系式； ②当 2＜x≤6 时，y 与 x 之间的函数关系式； ⑶探求⑵中得到的函数 y 在 x 取含何值时，存在最大值，并求出最大值. 【解答】 26．（满分 13 分）解：⑴ x，D 点；………………3 分 ⑵ ①当 0＜x≤2 时，△EFG 在梯形 ABCD 内部，所以 y＝ x2；………………6 分 ②分两种情况： Ⅰ.当 2＜x＜3 时，如图 1，点 E、点 F 在线段 BC 上， △EFG 与梯形 ABCD 重叠部分为四边形 EFNM， 2 3 2 x 2 x 2 3 ( )2 13 + 2 2 4 3 B E→ F→ C A D G ∵∠FNC＝∠FCN＝30°,∴FN＝FC＝6－2x.∴GN＝3x－6. 由于在 Rt△NMG 中，∠G＝60°， 所以，此时 y＝ x2－ （3x－6）2＝ .………………9 分 Ⅱ.当 3≤x≤6 时，如图 2，点 E 在线段 BC 上，点 F 在射线 CH 上， △EFG 与梯形 ABCD 重叠部分为△ECP， ∵EC＝6－x, ∴y＝ （6－x）2＝ .………………11 分 ⑶当 0＜x≤2 时，∵y＝ x2 在 x＞0 时，y 随 x 增大而增大， ∴x＝2 时，y 最大＝ ； 当 2＜x＜3 时，∵y＝ 在 x＝ 时，y 最大＝ ； 当 3≤x≤6 时，∵y＝ 在 x＜6 时，y 随 x 增大而减小， ∴x＝3 时，y 最大＝ .………………12 分 综上所述：当 x＝ 时，y 最大＝ .………………13 分 16、（2010 年福建省莆田市）24.（本小题满分 12 分） 如图 1，在 Rt 中， 点 D 在边 AB 上运动，DE 平分 交边 BC 于点 E， 垂足为 ，垂足为 N. 4 3 8 3 2 39 2 39 8 37 2 −+− xx 8 3 2 39 2 33 8 3 2 +− xx 4 3 3 2 39 2 39 8 37 2 −+− xx 7 18 7 39 2 39 2 33 8 3 2 +− xx 8 39 7 18 7 39 ABC△ 90 6 8ACB AC BC∠ = = =°， ， ， CDB∠ CM BD⊥ M EN CD⊥， B E F C A D G N M 图 1 B E C F A D G P H 图 2 第 24 题 （1）当 AD=CD 时，求证： ； （2）探究：AD 为何值时， 与 相似？ （3）探究：AD 为何值时，四边形 MEND 与 的面积相等？ 24．（本小题满分 12 分） （1）证明： ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 又∵DE 是∠BDC 的平分线 ∴∠BDC=2∠BDE ∴∠DAC=∠BDE∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 ∴DE∥AC ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 （2）解：（Ⅰ）当 时，得 ∴BD=DC ∵DE 平分∠BDC ∴DE⊥BC，BE=EC. 又∠ACB=90° ∴DE∥AC. ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 ∴ 即 ∴AD=5∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 （Ⅱ）当 时，得 ∴EN∥BD 又∵EN⊥CD ∴BD⊥CD 即 CD 是△ABC 斜边上的高∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 由三角形面积公式得 AB·CD=AC·BC ∴CD= ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 综上，当 AD=5 或 时，△BME 与△CNE 相似. （3）由角平分线性质易得 即 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 ∴EM 是 BD 的垂直平分线. ∴∠EDB=∠DBE ∵∠EDB=∠CDE ∴∠DBE=∠CDE 又∵∠DCE=∠BCD ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9 分 ∙∙∙∙∙∙∙∙∙∙∙∙∙10 分 DE AC∥ BME△ CNE△ BDE△ AD CD DAC DCA= ∴∠ = ∠ 2BDC DAC∴∠ = ∠ BME CNE△ ∽△ MBE NCE∠ = ∠ BE BD BC AB = 2 21 1 52 2BD AB AC BC= = + = BME ENC△ ∽△ EBM CEN∠ = ∠ 24 5 2 2 18 5AD AC CD= − = 18 5 1 2MDE DENS S DM ME= =△ △ · BDEMENDS S= △四边形 1 2 BD EM DM EM∴ =· · 1 2DM BD= CDE CBD△ ∽△ CD CE DE BC CD BD ∴ = = ① 2 CD BE BE BC BD BM ∴ = = 第 24 题 第 24 题 即 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11 分 由 式得 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12 分 17、（2010 年福建省莆田市）25．（本小题满分 14 分） 如图 1，在平面直角坐标系 xOy 中，矩形 OABC 的边 OA 在 y 轴的正半轴上，OC 在 x 轴的正半轴上， OA=1，OC=2，点 D 在边 OC 上且 . （1）求直线 AC 的解析式； （2）在 y 轴上是否存在点 P，直线 PD 与矩形对角线 AC 交于点 M，使得 为等腰三角形？若 存在，直接写出所有符合条件的点 P 的坐标；若不存在，请说明理由. （3）抛物线 经过怎样平移，才能使得平移后的抛物线过点 D 和点 E（点 E 在 y 轴正半轴 上），且 沿 DE 折叠后点 O 落在边 AB 上 处？ 【解答】 25．（本小题满分 14 分） 解：（1）OA=1，OC=2 则 A 点坐标为（0，1），C 点坐标为（2，0） 设直线 AC 的解析式为 y=kx+b 解得 4BECD BM = 4 5cos 4 55 4 BMB CDBE = = ∴ = × = ① 2 25 8 CDCE BC = = 39 4 39 39cos8 5 8 10BE BM BE B∴ = ∴ = = × = 39 112 10 2 10 5AD AB BM∴ = − = − × = 5 4OD = DMC△ 2y x= − ODE△ O′ 0 1 2 0 b k b + =∴ + = 1 2 1 k b  = −  = 第 25 题 直线 AC 的解析式为 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 （2） 或 （正确一个得 2 分）∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 （3）如图，设 过 点作 于 F 由折叠知 或 2 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10 分 18、（2010 年福建省泉州市）25．（12 分）我们容易发现：反比例函数的图象是一个中心对称图形.你 可以利用这一结论解决问题. 如图，在同一直角坐标系中，正比例函数的图象可以看作是：将 轴所在的直线绕着原点 逆时针旋 转α度角后的图形.若它与反比例函数 的图象分别交于第一、三象限的点 、 ，已知点 、 . （1）直接判断并填写：不论α取何值，四边形 的形状一定是 ; （2）①当点 为 时，四边形 是矩形，试求 、α、和 有值； ②观察猜想：对①中的 值，能使四边形 为矩形的点 共有几个？(不必说理) （3）试探究：四边形 能不能是菱形？若能, 直接写出 B 点的坐标, 若不能, 说明理由. 【解答】 25.（本小题 12 分） 解：（1）平行四边形 …………（3 分） （2）①∵点 在 的图象上，∴ ∴ ………………………………（4 分） 过 作 ，则 ∴ 1 12y x= − + 1 2 3 5 5 5(0 ) (0 ) (0 ( 5 2))3 8 4P P P− − +， ， ， ， ， 3 5(0 ) 4( 5 2) P − −， ( 1)O x′， O′ O F OC⊥′ 2 2 2 251 ( )4O D O F DF x= ′ + = + −′ OD O D= ′ 2 25 51 ( ) ( )4 4x∴ + − = 1 2x∴ = x O xy 3= B D )0,( mA − )0,(mC ABCD B )1,( p ABCD p m m ABCD B ABCD )1,( pB xy 3= p 31 = 3=p B ExBE 轴于⊥ 13 == ，BEOE 第 25 题 在 中， α=30° ……………………………………………………………（5 分） ∴ 又∵点 B、D 是正比例函数与反比例函数图象的交点， ∴点 B、D 关于原点 O 成中心对称 ………………………………………（6 分） ∴OB=OD= ∵四边形 为矩形，且 ∴ ………………………………………………………（7 分） ∴ ； ……………………………………………………………（8 分） ②能使四边形 为矩形的点 B 共有 2 个；………………………………（9 分） （3）四边形 不能是菱形. ……………………………………………（10 分） 法一：∵点 、 的坐标分别为 、 ∴四边形 的对角线 在 轴上. 又∵点 、 分别是正比例函数与反比例函数在第一、三象限的交点. ∴对角线 与 不可能垂直. ∴四边形 不能是菱形 法二：若四边形 ABCD 为菱形，则对角线 AC⊥BD，且 AC 与 BD 互相平分， 因为点 A、C 的坐标分别为（-m，0）、（m，0） 所以点 A、C 关于原点 O 对称，且 AC 在 x 轴上. ……………………………………（11 分） 所以 BD 应在 y 轴上，这与“点 B、D 分别在第一、三象限”矛盾， 所以四边形 ABCD 不可能为菱形. ……………………………………………………（12 分） 19 、 （ 2010 年 福 建 省 泉 州 市 ）26. （ 14 分 ）如 图 所 示 ， 已 知 抛 物 线 的图象与 轴相交于点 ，点 在该抛物线图象上，且以 为直径的⊙ 恰 好经过顶点 . （1）求 的值; （2）求点 的坐标； （3）若点 的纵坐标为 ，且点 在该抛物线的对称轴 上运动，试探 索： ①当 时，求 的取值范围（其中： 为△ 的面积， 为△ 的面积， 为四边 形 OACB 的面积）； ②当 取何值时，点 在⊙ 上.（写出 的值即可） 【解答】 26.（本小题 14 分） BOERt∆ 3 3 3 1tan === OE BEα 2=OB 2 ABCD )0,( mA − )0,(mC 2==== ODOCOBOA 2=m ABCD ABCD A C )0,( m− )0,(m ABCD AC x B D AC BD ABCD kxxy +−= 2 4 1 y )1,0(B ( , )C m n BC M A k C P t P l 1 2S S S< < t S PAB 1S OAB 2S t P M t 解：（1）∵点 B（0，1）在 的图象上，∴ ………………（2 分） ∴k=1………………（3 分） （2）由（1）知抛物线为： ∴顶点 A 为（2，0） …………（4 分） ∴OA=2，OB=1 过 C（m，n）作 CD⊥x 轴于 D，则 CD=n，OD=m，∴AD=m-2 由已知得∠BAC=90° …………………（5 分） ∴∠CAD+∠BAO=90°，又∠BAO+∠OBA=90°∴∠OBA=∠CAD ∴Rt△OAB∽Rt△DCA ∴ (或 tan∠OBA= tan∠CAD )…（6 分） ∴n=2(m-2)； 又点 C（m,n）在 上，∴ ∴ ，即 ∴m=2 或 m=10；当 m=2 时，n=0, 当 m=10 时，n=16；…………………（7 分） ∴符合条件的点 C 的坐标为（2，0）或（10，16）…（8 分） （3）①依题意得，点 C（2，0）不符合条件，∴点 C 为（10，16） 此时 ……………………………… （9 分） 又点 P 在函数 图象的对称轴 x=2 上，∴P（2,t），AP= ∴ = ……………………………（10 分） ∵ ∴当 t≥0 时，S=t，∴1﹤t﹤21. ………………（11 分） ∴当 t﹤0 时，S=-t，∴-21﹤t﹤-1 ∴t 的取值范围是：1﹤t﹤21 或-21﹤t﹤-1 …………（12 分） ②t=0，1，17. ……………………………………（14 分） 20、（2010 年福建省漳州市）25．（满分 13 分）如图，在△ABC 中，∠C=90°，AC=4cm，BC=5cm， 点 D 在 BC 上，且 CD=3cm．动点 P、Q 分别从 A、C 两点同时出发，其中点 P 以 1cm/s 的速度沿 AC 向 终点 C 移动；点 Q 以 cm/s 的速度沿 CB 向终点 B 移动．过 P 作 PE∥CB 交 AD 于点 E，设动点的运动 时间为 x 秒． （1）用含 x 的代数式表示 EP； （2）当 Q 在线段 CD 上运动几秒时，四边形 PEDQ 是平行四边形； （3）当 Q 在线段 BD（不包括点 B、点 D）上运动时，求四边形 EPDQ 面积的最大值． kxxy +−= 2 4 1 k+−×= 004 11 2 22 )2(4 114 1 −=+−= xyxxy 即 21 2 nm， OA CD OB AD =−= 即 21 2 −== m n， AD CD OB OA 即 2)2(4 1 −= xy 2)2(4 1 −= mn 2)2(4 1)2(2 −=− mm 0)10)(2(8 =−− mm 12 1 1 =×= OBOAS 212 =−= ∆ACDBODC SSS 2)2(4 1 −== xy APAPOAS =×= 2 1 21 SSS ≤≤ 5 4 t t 【解答】 25．解：（1）∵PE∥CB，∴∠AEP=∠ADC 又∵∠EAP=∠DAC，∴△AEP∽△ADC ……………………………………2 分 ∴ ，∴ …………3 分 ∴ ．…………………………4 分 （2）由四边形 PEDQ1 是平行四边形， 可得 EP=DQ1.………………………5 分 即 ， 所以 ．…………………………6 分 ∵0 < x < 2.4……………………………7 分 ∴当 Q 在线段 CD 上运动 1.5 秒时，四边形 PEDQ 是平行四边形.……8 分 （3） ……………………9 分 ………………………………10 分 又∵2.4 < x < 4，………………………………………………12 分 ∴当 时，S 取得最大值，最大值为 .………………13 分 26、（2010 年福建省漳州市）26．（满分 14 分）如图，直线 分别交 x 轴、y 轴于 A、B 两点，△ AOB 绕点 O 按逆时针方向旋转 90°后得到△DOC，抛物线 经过 A、B、C 三点． （1）填空：A（ ， ）、B（ ， ）、C（ ， ）； （2）求抛物线的函数关系式； （3）E 为抛物线的顶点，在线段 DE 上是否存在点 P，使得以 C、D、P 为顶点的三角形与△DOC 相似？ 若存在，请求出点 P 的坐标；若不存在，请说明理由. AP EP AC DC = 3 4 EP x= 3 4EP x= 3 534 4x x= − 1.5x = 2 1 3 5( 3) (4 )2 4 4S x x x= + − ⋅ −四边形EPDQ 2 11 62x x= − + − 11 4x = 25 16 3 3y x= − − 2y ax bx c= + + 【解答】 26.（满分 14 分） （1）A（－1，0），B（0，－3），C（3，0）……………………………………3 分 （2）∵抛物线 经过 B 点，∴c=－3. 又∵抛物线经过 A，C 两点，∴ 解得 ………………5 分 ∴ ……………………………………………………………………6 分 （3）解：过点 E 作 EF⊥y 轴垂足为点 F. 由（2）得 ∴E（1，—4）。 ∵tan∠EDF= ，tan∠DCO= . ∴∠EDF=∠DCO………………………7 分 ∵∠DCO+∠ODC=90°， ∴∠EDF+∠ODC=90°. ∴∠EDC=90°， ∴∠EDC=∠DOC.……………………8 分 ① 当 时，△ODC∽△DPC， 则 ，∴DP= …………………9 分 过点 P 作 PG⊥y 轴，垂足为点 G. ∵tan∠EDF= ，∴设 PG=x，则 DG=3x 在 Rt△DGP 中，DG2+PG2=DP2. ∴ ，∴ （不合题意，舍去）………………10 分 2y ax bx c= + + 3 0, 9 3 3 0. a b a b − − =  + − = 1, 2. a b =  = − 2 2 3y x x= − − 2 22 3 ( 1) 4y x x x= − − = − − 1 3 1 3 OC OD CD DP = 3 1 10 DP = 10 3 1 3 PG DG = 2 2 109 9x x+ = 1 2 1 1,3 3x x= = − 又∵OG=DO+DG=1+1=2，∴P（ ， ）．…………………………………11 分 ② 当 时，△ODC∽△DCP，则 ∴DP= . ∵DE= ，∴DP= （不合题意，舍去）…………13 分 综上所述，存在点 P，使得以 C、D、P 为顶点的三角形与△DOC 相似，此时点 P 的坐标为 P（ ， ）．……………………………………………………14 分 1 3 2− OC OD DP CD = 3 1 10DP = 3 10 21 3 10+ = 3 10 1 3 2−