中考数学综合题型专题复习卷新定义和阅读理解型问题 19页

新定义和阅读理解型问题 一、单选题 1 ． 已 知 : 表 示 不 超 过 的 最 大 整 数 ， 例 : ， 令 关 于 的 函 数 ( 是正整数)，例： =1，则下列结论错误的是（ ） A． B． C． D． 或 1 【答案】C 2．设 a，b 是实数，定义@的一种运算如下： ，则下列结论： ①若 ，则 a=0 或 b=0； ② ； ③不存在实数 a，b，满足 ； ④设 a，b 是矩形的长和宽，若矩形的周长固定，则当 a=b 时， 最大． 其中正确的是（　　） A．②③④　　　　B．①③④　　　　C．①②④　　　　D．①②③ 【答案】C． 3．在△ABC 中，若 O 为 BC 边的中点，则必有：AB2+AC2=2AO2+2BO2 成立．依据以上结论， 解决如下问题：如图，在矩形 DEFG 中，已知 DE=4，EF=3，点 P 在以 DE 为直径的半圆 上运动，则 PF2+PG2 的最小值为（　　） A． B． C．34 D．10 ( ) ( )2 2@a b a b a b= + − − @ 0a b = ( )@ @ @a b c a b a c+ = + 2 2@ 5a b a b= + @a b 【答案】D 4．我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正 方形和两对全等的直角三角形，得到一个恒等式．后人借助这种分割方法所得的图形 证明了勾股定理，如图所示的矩形由两个这样的图形拼成，若 a=3，b=4，则该矩形的 面积为（ ） A．20 B．24 C． D． 【答案】B 5．阅读理解： ， ， ， 是实数，我们把符号 称为 阶行列式，并且规定： ， 例 如 ： . 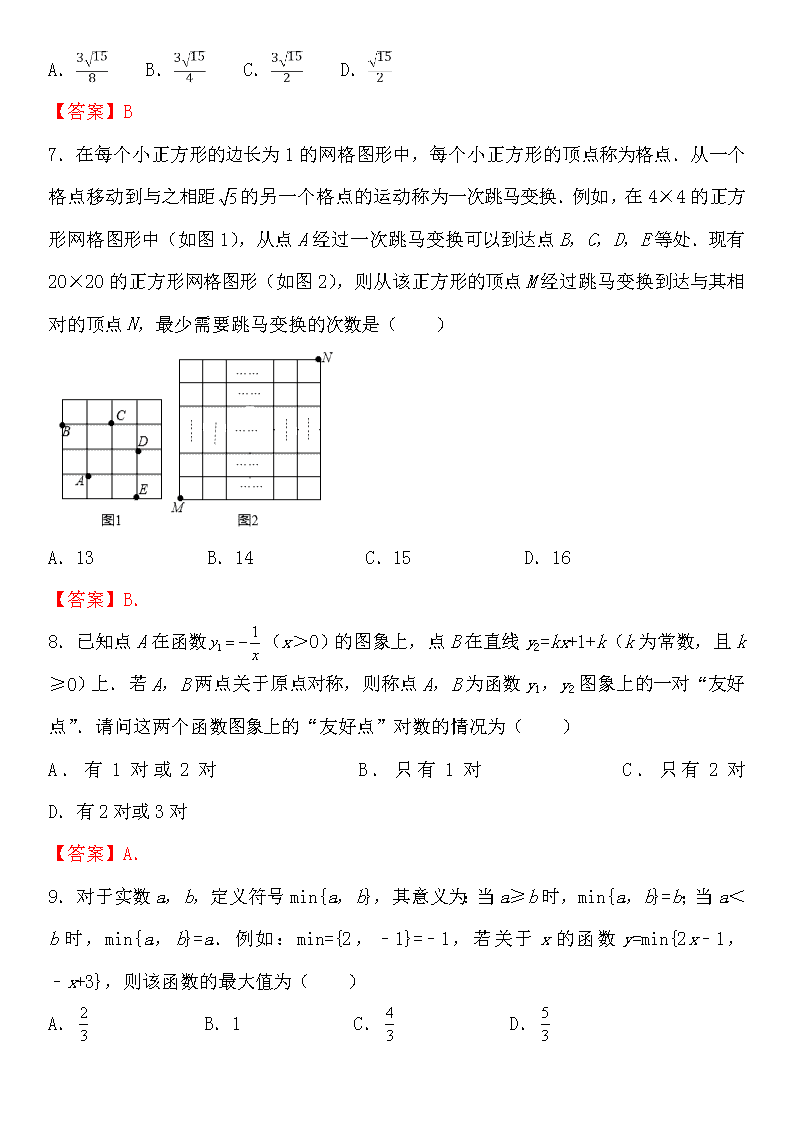二 元 一 次 方 程 组 的解可以利用 阶行列式表示为： ；其中 ， ， .问题：对于用上面的方法解二元一次方程组 时，下面说法错误的 是（ ） A． B． C． D．方程组的解为 【答案】C 6．已知三角形的三边长分别为 a、b、c，求其面积问题，中外数学家曾经进行过深入 研究，古希腊的几何学家海伦（Heron，约公元 50 年）给出求其面积的海伦公式 S= ，其中 p= ；我国南宋时期数学家秦九韶（约 1202-1261）曾提 出利用三角形的三边求其面积的秦九韶公式 S= ，若一个三角形的三 边长分别为 2，3，4，则其面积是（ ） A． B． C． D． 【答案】B 7．在每个小正方形的边长为 1 的网格图形中，每个小正方形的顶点称为格点．从一个 格点移动到与之相距 的另一个格点的运动称为一次跳马变换．例如，在 4×4 的正方 形网格图形中（如图 1），从点 A 经过一次跳马变换可以到达点 B，C，D，E 等处．现有 20×20 的正方形网格图形（如图 2），则从该正方形的顶点 M 经过跳马变换到达与其相 对的顶点 N，最少需要跳马变换的次数是（　　） A．13　　　　　　B．14　　　　　　C．15　　　　　　D．16 【答案】B． 8．已知点 A 在函数 （x＞0）的图象上，点 B 在直线 y2=kx+1+k（k 为常数，且 k ≥0）上．若 A，B 两点关于原点对称，则称点 A，B 为函数 y1，y2 图象上的一对“友好 点”．请问这两个函数图象上的“友好点”对数的情况为（　　） A ． 有 1 对 或 2 对 　 　 　 　 　 　 B ． 只 有 1 对 　 　 　 　 　 　 C ． 只 有 2 对　　　　　　 D．有 2 对或 3 对 【答案】A． 9．对于实数 a，b，定义符号 min{a，b}，其意义为：当 a≥b 时，min{a，b}=b；当 a＜ b 时，min{a，b}=a．例如：min={2，﹣1}=﹣1，若关于 x 的函数 y=min{2x﹣1， ﹣x+3}，则该函数的最大值为（　　） A． 　　　　　　B．1　　　　　　C． 　　　　　　D． 5 1 1y x = − 2 3 4 3 5 3 【答案】D． 10．根据如图所示的程序计算函数 y 的值，若输入的 x 值是 4 或 7 时，输出的 y 值相 等，则 b 等于（　　） A．9 B．7 C．﹣9 D．﹣7 【答案】C 11．已知二次函数 y=﹣x2+x+6 及一次函数 y=﹣x+m，将该二次函数在 x 轴上方的图象 沿 x 轴翻折到 x 轴下方，图象的其余部分不变，得到一个新函数（如图所示），请你在 图中画出这个新图象，当直线 y=﹣x+m 与新图象有 4 个交点时，m 的取值范围是（　　） A．﹣ ＜m＜3 B．﹣ ＜m＜2 C．﹣2＜m＜3 D．﹣6＜m＜﹣2 【答案】D 12．如图，一段抛物线 y=﹣x2+4（﹣2≤x≤2）为 C1，与 x 轴交于 A0，A1 两点，顶点为 D1；将 C1 绕点 A1 旋转 180°得到 C2，顶点为 D2；C1 与 C2 组成一个新的图象，垂直于 y 轴的直线 l 与新图象交于点 P1（x1，y1），P2（x2，y2），与线段 D1D2 交于点 P3（x3， y3），设 x1，x2，x3 均为正数，t=x1+x2+x3，则 t 的取值范围是（　　） A．6＜t≤8 B．6≤t≤8 C．10＜t≤12 D．10≤t≤12 【答案】D 13．如图，抛物线 与 x 轴交于点 A、B，把抛物线在 x 轴及其下方的部分记 作 ，将 向左平移得到 ， 与 x 轴交于点 B、D，若直线 与 、 共有 3 个不 同的交点，则 m 的取值范围是 　　 A． B． C． D． 【答案】C 14．定义一种对正整数 n 的“F”运算：①当 n 为奇数时，F（n）=3n+1；②当 n 为偶 数时，F（n）= （其中 k 是使 F（n）为奇数的正整数）……，两种运算交替重复进行， 例如，取 n=24，则： 若 n=13，则第 2018 次“F”运算的结果是（　　） A．1 B．4 C．2018 D．42018 【答案】A 15．在求 1+6+62+63+64+65+66+67+68+69 的值时，小林发现：从第二个加数起每一个加数 都是前一个加数的 6 倍，于是她设： S=1+6+62+63+64+65+66+67+68+69① 然后在①式的两边都乘以 6，得： 6S=6+62+63+64+65+66+67+68+69+610② ②﹣①得 6S﹣S=610﹣1，即 5S=610﹣1，所以 S= ，得出答案后，爱动脑筋的小林想： 如果把“6”换成字母“a”（a≠0 且 a≠1），能否求出 1+a+a2+a3+a4+…+a2014 的值？你 的答案是（　　） A． B． C． D．a2014﹣1 【答案】B 二、填空题 16．对于实数 a，b，定义运算“◆”：a◆b= ，例如 4◆3，因为 4＞3．所 以 4◆3= =5．若 x，y 满足方程组 ，则 x◆y=_____________. 【答案】60 17．观察下列运算过程：S=1+3+32+33+…+32017+32018 ①， ①×3 得 3S=3+32+33+…+32018+32019 ②， ②﹣①得 2S=32019﹣1，S= ． 运用上面计算方法计算：1+5+52+53+…+52018=____． 【答案】 18．对于任意实数 a、b，定义：a◆b=a2+ab+b2．若方程（x◆2）﹣5=0 的两根记为 m、 n，则 m2+n2=　 　． 【答案】6． 19．规定： ，如： ，若 ，则 ＝__. 【答案】1 或-3 20 ． 对 于 实 数 a ， b ， 定 义 运 算 “※” 如 下 ： a※b=a2﹣ab ， 例 如 ， 5※3=52 ﹣ 5×3=10．若（x+1）※（x﹣2）=6，则 x 的值为_____． 【答案】1 21．我国南宋著名数学家秦九韶在他的著作《数书九章》一书中，给出了著名的秦九 韶公式，也叫三斜求积公式，即如果一个三角形的三边长分别为 a，b，c，则该三角形 的面积为 S= ．现已知△ABC 的三边长分别为 1，2， ，则△ABC 的 面积为______． 【答案】1 22．对于一个位置确定的图形，如果它的所有点都在一个水平放置的矩形内部或边上， 且该图形与矩形的每条边都至少有一个公共点（如图 1），那么这个矩形水平方向的边 长称为该图形的宽，铅锤方向的边长称为该矩形的高．如图 2，菱形 ABCD 的边长为 1， 边 AB 水平放置．如果该菱形的高是宽的 ，那么它的宽的值是_____． 【答案】 23．对于任意实数 a、b，定义一种运算：a※b=ab﹣a+b﹣2．例如，2※5=2×5﹣2+5﹣ 2=ll．请根据上述的定义解决问题：若不等式 3※x＜2，则不等式的正整数解是 _____． 【答案】1 24．如图，把平面内一条数轴 x 绕原点 O 逆时针旋转角 θ（0°＜θ＜90°）得到另一 条数轴 y，x 轴和 y 轴构成一个平面斜坐标系．规定：过点 P 作 y 轴的平行线，交 x 轴 于点 A，过点 P 作 x 轴的平行线，交 y 轴于点 B，若点 A 在 x 轴上对应的实数为 a，点 B 在 y 轴上对应的实数为 b，则称有序实数对（a，b）为点 P 的斜坐标，在某平面斜坐标 系中，已知 θ=60°，点 M′的斜坐标为（3，2），点 N 与点 M 关于 y 轴对称，则点 N 的 斜坐标为_____． 【答案】（﹣2，5） 25．如图 1，作∠BPC 平分线的反向延长线 PA，现要分别以∠APB，∠APC，∠BPC 为内 角作正多边形，且边长均为 1，将作出的三个正多边形填充不同花纹后成为一个图 案．例如，若以∠BPC 为内角，可作出一个边长为 1 的正方形，此时∠BPC=90°，而 =45 是 360°（多边形外角和）的 ，这样就恰好可作出两个边长均为 1 的正八边形， 填充花纹后得到一个符合要求的图案，如图 2 所示． 图 2 中的图案外轮廓周长是_____； 在所有符合要求的图案中选一个外轮廓周长最大的定为会标，则会标的外轮廓周长是 _____． 【答案】 14 21 26．若 为实数，则 表示不大于 的最大整数，例如 ， ， 等. 是大于 的最小整数，对任意的实数 都满足不等式 . ①，利用这个不等式 ①，求出满足 的所有解，其所有解为__________． 【答案】 或 1. 27．《九章算术》是我国古代数学名著，书中有下列问题：“今有勾五步，股十二步， 问勾中容方几何？”其意思为：“今有直角三角形，勾（短直角边）长为 5 步，股（长 直角边）长为 12 步，问该直角三角形能容纳的正方形边长最大是多少步？”该问题的 答案是______步． 【答案】 ． 28．在每个小正方形的边长为 1 的网格图形中，每个小正方形的顶点称为格点．以顶 点都是格点的正方形 ABCD 的边为斜边，向内作四个全等的直角三角形，使四个直角顶 点 E，F，G，H 都是格点，且四边形 EFGH 为正方形，我们把这样的图形称为格点弦 图．例如，在如图 1 所示的格点弦图中，正方形 ABCD 的边长为 ，此时正方形 EFGH 的而积为 5．问：当格点弦图中的正方形 ABCD 的边长为 时，正方形 EFGH 的面积的 所有可能值是_____（不包括 5）． 【答案】9 或 13 或 49. 29．刘徽是中国古代卓越的数学家之一，他在《九章算术》中提出了“割圆术”，即用 内接或外切正多边形逐步逼近圆来近似计算圆的面积，设圆 O 的半径为 1，若用圆 O 的 外切正六边形的面积来近似估计圆 O 的面积，则 S=_____．（结果保留根号） 【答案】 30．定义新运算：a※b=a2+b，例如 3※2=32+2=11，已知 4※x=20，则 x=_____． 【答案】4 31．设双曲线 与直线 交于 ， 两点（点 在第三象限），将双曲线在第一象 限的一支沿射线 的方向平移，使其经过点 ，将双曲线在第三象限的一支沿射线 的 方向平移，使其经过点 ，平移后的两条曲线相交于点 ， 两点，此时我们称平移后的 两条曲线所围部分（如图中阴影部分）为双曲线的“眸”， 为双曲线的“眸径”.当 双曲线 的眸径为 6 时， 的值为__________. 【答案】 32．如图，若△ABC 内一点 P 满足∠PAC=∠PCB=∠PBA，则称点 P 为△ABC 的布罗卡尔 点，三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现，后来被数学爱 好者法国军官布罗卡尔重新发现，并用他的名字命名，布罗卡尔点的再次发现，引发 了研究“三角形几何”的热潮．已知△ABC 中，CA=CB，∠ACB=120°，P 为△ABC 的布 罗卡尔点，若 PA= ，则 PB+PC=_____． 【答案】1+ ． 三、解答题 33．综合与实践 折纸是一项有趣的活动，同学们小时候都玩过折纸，可能折过小动物、小花、飞机、 小船等，折纸活动也伴随着我们初中数学的学习． 在折纸过程中，我们可以通过研究图形的性质和运动、确定图形位置等，进一步发展 空间观念，在经历借助图形思考问题的过程中，我们会初步建立几何直观，折纸往往 从矩形纸片开始，今天，就让我们带着数学的眼光来玩一玩折纸，看看折叠矩形的对 角线之后能得到哪些数学结论． 实践操作 如图 1，将矩形纸片 ABCD 沿对角线 AC 翻折，使点B′落在矩形 ABCD 所在平面内，B′C 和 AD 相交于点 E，连接 B′D． 解决问题 (1)在图 1 中， ①B′D 和 AC 的位置关系为　　； ②将△AEC 剪下后展开，得到的图形是　　； (2)若图 1 中的矩形变为平行四边形时(AB≠BC)，如图 2 所示，结论①和结论②是否成 立，若成立，请挑选其中的一个结论加以证明，若不成立，请说明理由； (3)小红沿对角线折叠一张矩形纸片，发现所得图形是轴对称图形，沿对称轴再次折叠 后，得到的仍是轴对称图形，则小红折叠的矩形纸片的长宽之比为　　； 拓展应用 (4)在图 2 中，若∠B=30°，AB=4 ，当△AB′D 恰好为直角三角形时，BC 的长度 为　　． 【答案】(1)①BD′//AC，菱形；(2)见解析；(3)1：1 或 ：1；(4)4 或 6 或 8 或 12. 34．如图①，在 Rt△ABC 中，以下是小亮探究 与 之间关系的方法： ∵sinA= ，sinB= ， ∴c= ，c= ， ∴ = ， 根据你掌握的三角函数知识．在图②的锐角△ABC 中，探究 、 、 之间的关系， 并写出探究过程． 【答案】 = = ，理由见解析. 35．如图，在平面直角坐标系中，矩形 ABCD 的对称中心为坐标原点 O，AD⊥y 轴于点 E （点 A 在点 D 的左侧），经过 E、D 两点的函数 y=﹣ x2+mx+1（x≥0）的图象记为 G1， 函数 y=﹣ x2﹣mx﹣1（x＜0）的图象记为 G2，其中 m 是常数，图象 G1、G2 合起来得到 的图象记为 G．设矩形 ABCD 的周长为 L． （1）当点 A 的横坐标为﹣1 时，求 m 的值； （2）求 L 与 m 之间的函数关系式； （3）当 G2 与矩形 ABCD 恰好有两个公共点时，求 L 的值； （4）设 G 在﹣4≤x≤2 上最高点的纵坐标为 y0，当 ≤y0≤9 时，直接写出 L 的取值范 围． 【答案】（1） ；（2）L=8m+4．（3）20；（4）12≤L≤44． 36．我们不妨约定：对角线互相垂直的凸四边形叫做“十字形”． （1）①在“平行四边形，矩形，菱形，正方形”中，一定是“十字形”的有　 　； ②在凸四边形 ABCD 中，AB=AD 且 CB≠CD，则该四边形　 　“十字形”．（填“是” 或“不是”） （2）如图 1，A，B，C，D 是半径为 1 的⊙O 上按逆时针方向排列的四个动点，AC 与 BD 交于点 E，∠ADB﹣∠CDB=∠ABD﹣∠CBD，当 6≤AC2+BD2≤7 时，求 OE 的取值范围； （3）如图 2，在平面直角坐标系 xOy 中，抛物线 y=ax2+bx+c（a，b，c 为常数，a＞0， c＜0）与 x 轴交于 A，C 两点（点 A 在点 C 的左侧），B 是抛物线与 y 轴的交点，点 D 的 坐标为（0，﹣ac），记“十字形”ABCD 的面积为 S，记△AOB，△COD，△AOD，△BOC 的面积分别为 S1，S2，S3，S4．求同时满足下列三个条件的抛物线的解析式； ① = ；② = ；③“十字形”ABCD 的周长为 12 ． 【答案】（1）①菱形，正方形；②不是；（2） （OE＞0）；（3）y=x2﹣9． 37．若一个三角形一条边的平方等于另两条边的乘积，我们把这个三角形叫做比例三 角形． 已知 是比例三角形， ， ，请直接写出所有满足条件的 AC 的长； 如图 1，在四边形 ABCD 中， ，对角线 BD 平分 ， 求证： 是比例三角形． 如图 2，在 的条件下，当 时，求 的值． 【答案】 当 或 或 时， 是比例三角形； 证明见解析； ． 38．定义： 我们知道，四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形 相似（不全等），我们就把这条对角线叫做这个四边形的“相似对角线”． 理解： （1）如图 1，已知 Rt△ABC 在正方形网格中，请你只用无刻度的直尺在网格中找到一 点 D，使四边形 ABCD 是以 AC 为“相似对角线”的四边形（保留画图痕迹，找出 3 个即 可）； （2）如图 2，在四边形 ABCD 中，∠ABC=80°，∠ADC=140°，对角线 BD 平分∠ABC． 求证：BD 是四边形 ABCD 的“相似对角线”； （3）如图 3，已知 FH 是四边形 EFCH 的“相似对角线”，∠EFH=∠HFG=30°，连接 EG， 若△EFG 的面积为 2 ，求 FH 的长． 【答案】（1）见解析；（2）证明见解析；（3）FH=2 ． 39．对于三个数 a，b，c，用 M{a，b，c}表示这三个数的中位数，用 max{a，b，c}表 示这三个数中最大数，例如：M{﹣2，﹣1，0}=﹣1，max{﹣2，﹣1，0}=0，max{﹣2，﹣ 1，a}= 解决问题： （1）填空：M{sin45°，cos60°，tan60°}=__________，如果 max{3，5﹣3x，2x﹣ 6}=3，则 x 的取值范围为__________； （2）如果 2•M{2，x+2，x+4}=max{2，x+2，x+4}，求 x 的值； （3）如果 M{9，x2，3x﹣2}=max{9，x2，3x﹣2}，求 x 的值． 40．阅读短文，解决问题 如果一个三角形和一个菱形满足条件：三角形的一个角与菱形的一个角重合，且菱形 的这个角的对角顶点在三角形的这个角的对边上，则称这个菱形为该三角形的“亲密 菱形”.如图 1，菱形 AEFD 为△ABC 的“亲密菱形”. 如图 2，在△ABC 中，以点 A 为圆心，以任意长为半径作弧，交 AB、AC 于点 M、N，再 分别以 M、N 为圆心，以大于 MN 的长为半径作弧，两弧交于点 P，作射线 AP，交 BC 于 点 F，过点 F 作 FD//AC，FE//AB. (1)求证：四边形 AEFD 是△ABC 的“亲密菱形”； (2)当 AB=6，AC=12，∠BAC=45°时，求菱形 AEFD 的面积. 【答案】(1)证明见解析；(2) 四边形 的面积为 . 41．小贤与小杰在探究某类二次函数问题时，经历了如下过程： 求解体验 (1)已知抛物线 经过点(-1,0),则 = ，顶点坐标为 ， 该抛物线关于点(0,1）成中心对称的抛物线的表达式是 . 抽象感悟 我们定义：对于抛物线 ,以 轴上的点 为中心，作该抛物线 关于 点 对称的抛物线 ,则我们又称抛物线 为抛物线 的“衍生抛物线”，点 为“衍生中 心”. (2)已知抛物线 关于点 的衍生抛物线为 ，若这两条抛物线有交点， 求 的取值范围. 问题解决 (3) 已知抛物线 ①若抛物线 的衍生抛物线为 ,两抛物线有两个交点，且恰 好是它们的顶点，求 的值及衍生中心的坐标； ②若抛物线 关于点 的衍生抛物线为 ,其顶点为 ；关于点 的 衍生抛物线为 ，其顶点为 ；…；关于点 的衍生抛物线为 ，其顶点为 ；…( 为 正整数).求 的长(用含 的式子表示). 【答案】求解体验： ；顶点坐标是(-2,1)； ；抽象感悟： ；问题 解决：① ；（0，6）；② 42．结果如此巧合！ 下面是小颖对一道题目的解答. 题目：如图， 的内切圆与斜边 相切于点 ， ， ，求 的面积. 解：设 的内切圆分别与 、 相切于点 、 ， 的长为 . 根据切线长定理，得 ， ， . 根据勾股定理，得 . 整理，得 . 所以 . 小颖发现 恰好就是 ，即 的面积等于 与 的积.这仅仅是巧合吗? 请你帮她完成下面的探索. 已知： 的内切圆与 相切于点 ， ， . 可以一般化吗？ （1）若 ，求证： 的面积等于 . 倒过来思考呢？ （2）若 ，求证 .改变一下条件…… （3）若 ，用 、 表示 的面积. 【答案】（1）证明见解析；（2）证明见解析.（3） . 43．我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高 底”三角形,这条边叫做这个三角形的“等底”。 （1）概念理解: 如图 1,在 中, , . ,试判断 是否是“等高底”三角形，请说明 理由. （2）问题探究: 如图 2, 是“等高底”三角形, 是“等底”，作 关于 所在直线的对称图形得 到 ,连结 交直线 于点 .若点 是 的重心,求 的值. （3）应用拓展: 如图 3,已知 , 与 之间的距离为 2.“等高底” 的“等底” 在直线 上,点 在直线 上,有一边的长是 的 倍.将 绕点 按顺时针方向旋转 得到 , 所 在直线交 于点 .求 的值. 【答案】（1）证明见解析；（2） （3） 的值为 , ,2 44．阅读下面材料： 小明遇到这样一个问题： 如图 1，△ABC 中，∠ACB=90°，点 D 在 AB 上，且∠BAC=2∠DCB，求证：AC=AD． 小明发现，除了直接用角度计算的方法外，还可以用下面两种方法： 方法 1：如图 2，作 AE 平分∠CAB，与 CD 相交于点 E． 方法 2：如图 3，作∠DCF=∠DCB，与 AB 相交于点 F． （1）根据阅读材料，任选一种方法，证明 AC=AD． 用学过的知识或参考小明的方法，解决下面的问题： （2）如图 4，△ABC 中，点 D 在 AB 上，点 E 在 BC 上，且∠BDE=2∠ABC，点 F 在 BD 上， 且∠AFE=∠BAC，延长 DC、FE，相交于点 G，且∠DGF=∠BDE． ①在图中找出与∠DEF 相等的角，并加以证明； ②若 AB=kDF，猜想线段 DE 与 DB 的数量关系，并证明你的猜想． 【答案】（1）证明见解析；（2）∠DEF=∠FDG，证明见解析；②结论：BD=k•DE．理由见 解析.