山东省临沂市中考数学试题 真题word版 8页

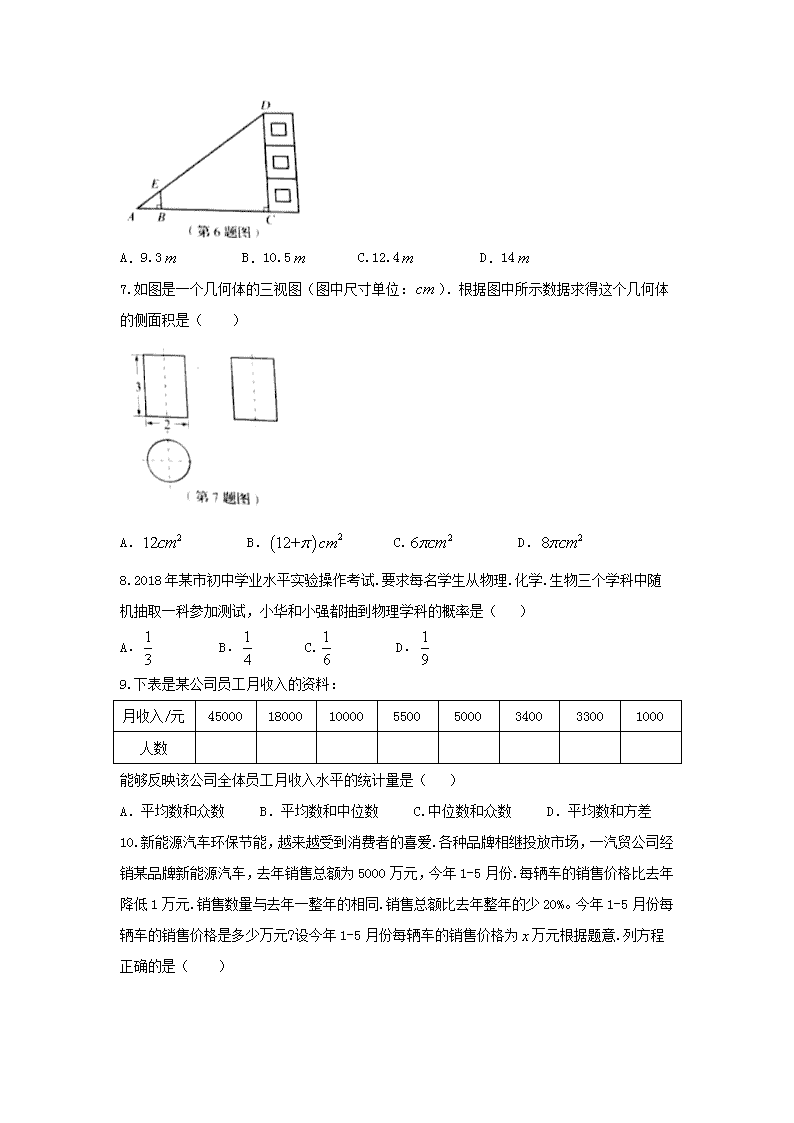
‎2018年临沂市初中学业水平考试试题 数学 第Ⅰ卷（共60分）‎ 一、选择题：本大题共14个小题,每小题3分,共42分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.在实数-3. -1. 0. 1中，最小的数是（ ）‎ A．-3 B．-1 C．0 D．1‎ ‎2.自2013年10月习近平总书记提出“精准扶贫”的重要思想以来，各地积极推进精准扶贫.‎ 加大帮扶力度，全国脱贫人口数不断增加，仅2017年我国减少的贫困人口就接近1100万 人， 将1100万人用科学记数法表示为 A． 人 B．人 C． 人 D．人 ‎3.如图，、,,则的度数是（ ）‎ A．42° B．64° C．74° D．106° ‎ ‎4.一元二次方程配方后可化为（ ）‎ A． B． C. D．‎ ‎5.不等式组的正整数解的个数是（ ）‎ A．5 B．4 C.3 D．2‎ ‎6.如图，利用标杆测量建筑物的高度．已知标杆高1.2，测得，．则建筑物的高是（ ）‎ A．9.3 B．10.5 C.12.4 D．14‎ ‎7.如图是一个几何体的三视图（图中尺寸单位：）．根据图中所示数据求得这个几何体的侧面积是（ ）‎ A． B． C. D．‎ ‎8.2018年某市初中学业水平实验操作考试.要求每名学生从物理.化学.生物三个学科中随机抽取一科参加测试，小华和小强都抽到物理学科的概率是（ ）‎ A． B． C. D．‎ ‎9.下表是某公司员工月收入的资料：‎ 月收入/元 ‎45000‎ ‎18000‎ ‎10000‎ ‎5500‎ ‎5000‎ ‎3400‎ ‎3300‎ ‎1000‎ 人数 能够反映该公司全体员工月收入水平的统计量是（ ）‎ A．平均数和众数 B．平均数和中位数 C.中位数和众数 D．平均数和方差 ‎10.新能源汽车环保节能，越来越受到消费者的喜爱.各种品牌相继投放市场，一汽贸公司经销某品牌新能源汽车，去年销售总额为5000万元，今年1-5月份.每辆车的销售价格比去年 降低1万元.销售数量与去年一整年的相同.销售总额比去年整年的少20%。今年1-5月份每辆车的销售价格是多少万元?设今年1-5月份每辆车的销售价格为万元根据题意.列方程正确的是（ ）‎ A． B． ‎ ‎ C. 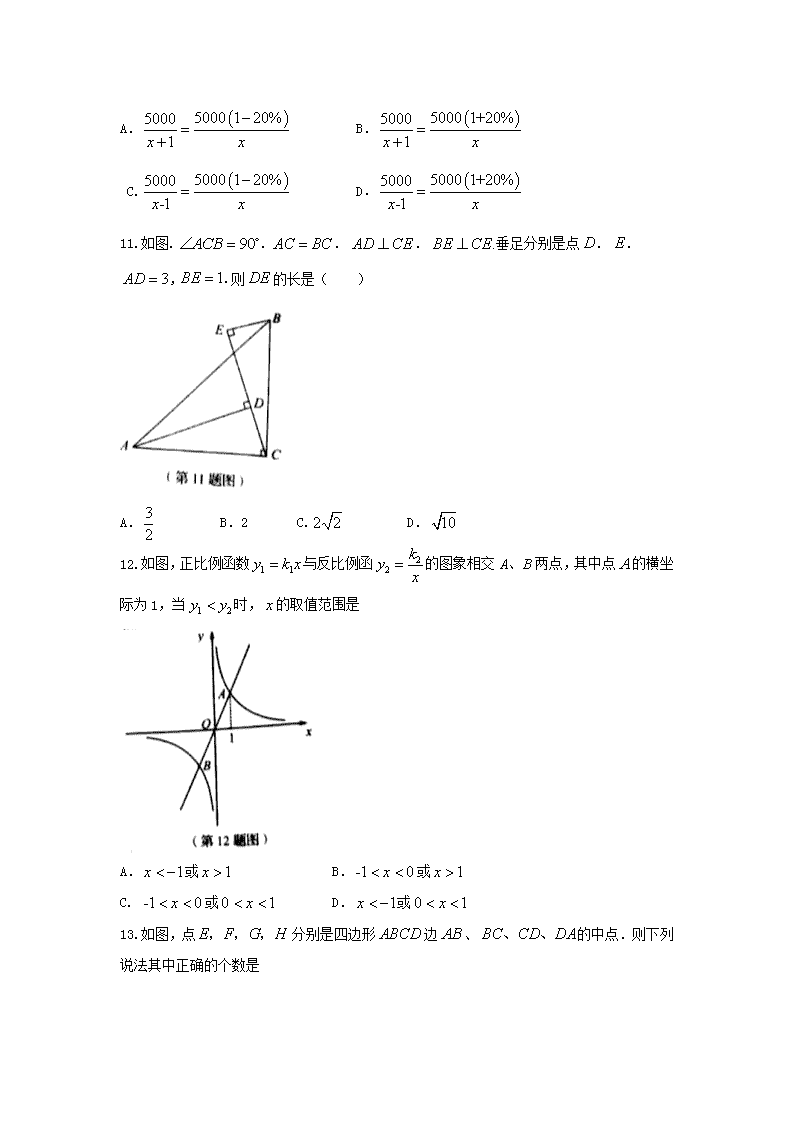D．‎ ‎11.如图... . 垂足分别是点. . ,.则的长是（ ）‎ A． B．2 C. D．‎ ‎12.如图，正比例函数与反比例函的图象相交两点，其中点的横坐际为1，当时，的取值范围是 A．或 B．或 ‎ C. 或 D．或 ‎13.如图，点分别是四边形边、的中点．则下列说法其中正确的个数是 ‎①若则四边形为矩形 ‎②若，四边形为菱形；‎ ‎③若边形是平行四边形，则与互相平分 ‎④若四边形是正方形，与互相垂直且相等 A.1 B.2 C.3 D.4‎ ‎14.一列自然数0，1，2，3，…，100．依次将该列数中的每一个数平方后除以100，得到 一列新数．则下列结论正确的是 A.原数与对应新数的差不可能等于零．‎ B.原数与对应新数的差，随着原数的增大而增大 C.当原数与对应新数的差等于21时，原数等于30‎ D.当原数取50时，原数与对应新数的差最大 第Ⅱ卷（共90分）‎ 二、填空题（每题3分，满分15分，将答案填在答题纸上）‎ ‎15.计算：= ．‎ ‎16.已知，则= ．‎ ‎17.如图、在中.， 、 .则= ．‎ ‎18.如图，在△中，. . 能够将△完全覆盖的最小圆形片的直径是 ．‎ ‎19.任何一个无限循环小数都可以写成分数的形式，应该怎样写呢?我们以无限循环小数，为例进行说明:设.由...可知，.... 所以方程.得，于是，得.‎ 将写成分数的形式是______________.‎ 三、解答题 （本大题共7小题，共63分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎20.计算： ‎ ‎21. 某地某月1-20日中午12时的气温（单位：℃）如下：‎ ‎（1）将下列频数分布表补充完整：‎ 气温分组 划记 频数 ‎3‎ ‎2‎ ‎(2)补全频数分布直方图:‎ ‎(3)根据频数分布表或频数分布直方图,分析数据的分布情况.‎ ‎22.如图，有一个三角形的钢架. . . .请计算说明，工人师傅搬运此钢架能否通过一个直径为2.1的圆形门?‎ ‎23.如图. 为等腰三角形，是底边的中点，腰与相切于点. 与相交于点 ‎(1)求证: 是的切线;‎ ‎(2)若，，求阴影部分的面积.‎ ‎24.甲、乙两人分别从A．B两地同时出发，匀速相向而行．甲的速度大于乙的速度，甲到 达地后．乙继续前行．设出发后，两人相距．图中折线表示从两人出发至乙到达地的过程中与之间的函数关系 根据图中信息，求：‎ ‎（1）点的坐标，并说明它的实际意义；‎ ‎（2）甲、乙两个的速度.‎ ‎25.将矩形 绕点时针旋转，得到矩形；‎ ‎（1）如图．当点在上时．求证：‎ ‎（2）当为何值时，？画出图形，并说明理由.‎ ‎26.如图，在平面直角坐杯系中．．．．点的坐标为，抛物线经过，两点 ‎（1）求抛线的解析式 ‎（2）点是直线上方抛物线上的一点．过点作垂直轴于点，交线段于 点，使．‎ ‎①求点的坐标 ‎②在直线上是否存在点，使△为直角三角形？若存在，求出符合条件的所有 点的坐标；若不存在．请说明理由.‎