2019届中考数学一轮复习 第34课时 动态几何导学案（无答案） 7页

第34课时 动态几何 班级： 姓名： ‎ 学习目标：1.用运动与变化的眼光去观察和研究图形，把握动点运动与变化的全过程。‎ ‎2.抓住其中的等量关系和变量关系，特别关注一些不变量、不变关系或特殊关系。‎ 重难点：抓住其中的等量关系和变量关系，特别关注一些不变量、不变关系或特殊关系。‎ 学习过程 一．基础演练：‎ ‎1.（2016荆门）如图，正方形的边长为，动点从点出发，在正方形的边上沿的方向运动到点停止，设点的运动路程为，在下列图象中，能表示△的面积关于的函数关系的图象是（　　）‎ A． B． C． D．‎ ‎2.（2017桂林）如图，在菱形中，，，点是边上的动点，过点作直线的垂线，垂足为，当点从点运动到点时，点的运动路径长为（　　）‎ A. B‎.2 ‎C. D. 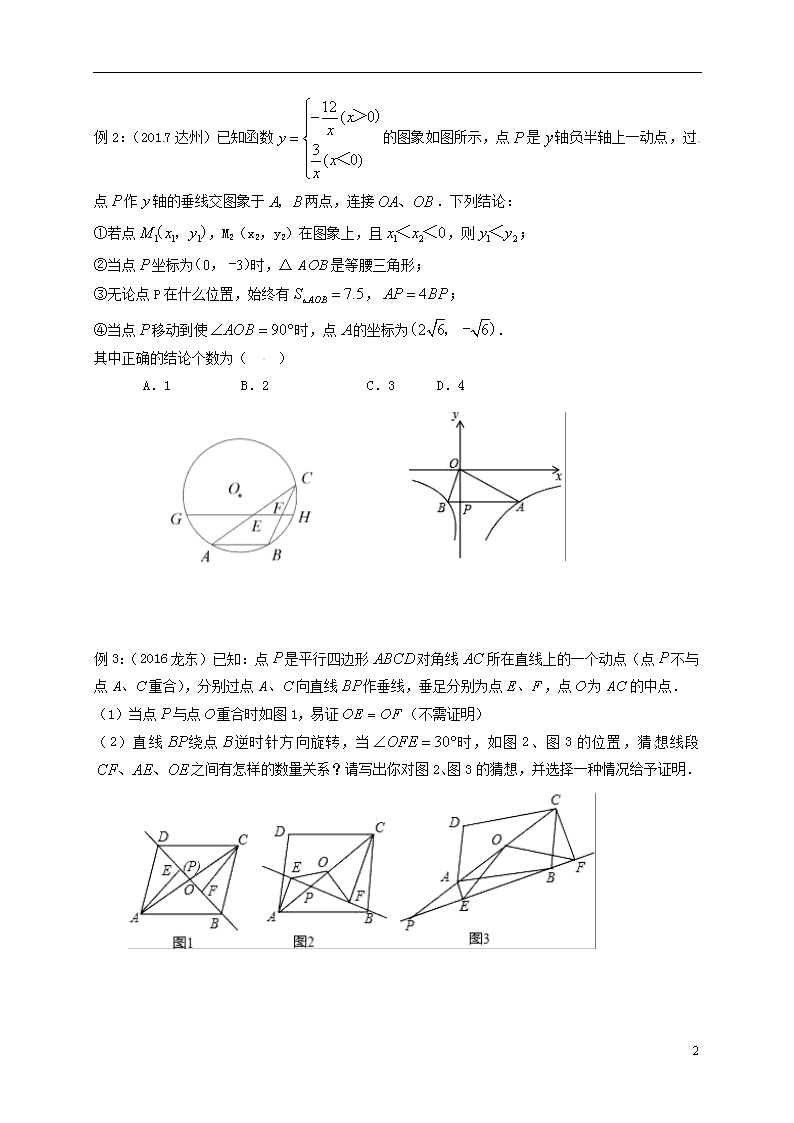‎ ‎3.（2017贵阳）如图，在矩形纸片中，，，点是的中点，点是边上的一个动点，将△沿所在直线翻折，得到△，则的长的最小值是 ．‎ ‎4.（2015鄂州）如图，在矩形中，，，点是的中点，连接，将△沿折叠，点落在点处，连接，则（ ）‎ A． B． F D A E C B C． D．‎ 二、典型例题 例1：（2013陕西）如图，AB是⊙的一条弦，点是⊙上一动点，且，点分别是的中点，直线与⊙交于两点.若⊙的半径为7，则的最大值为 . ‎ 6‎ 例2：（2017达州）已知函数的图象如图所示，点是轴负半轴上一动点，过点作轴的垂线交图象于两点，连接．下列结论：‎ ‎①若点，M2（x2，y2）在图象上，且，则；‎ ‎②当点坐标为时，△是等腰三角形；‎ ‎③无论点P在什么位置，始终有，；‎ ‎④当点移动到使时，点的坐标为．‎ 其中正确的结论个数为（　　）‎ A．1 B．‎2 ‎C．3 D．4‎ 例3：（2016龙东）已知：点是平行四边形对角线所在直线上的一个动点（点不与点重合），分别过点向直线作垂线，垂足分别为点，点为的中点．‎ ‎（1）当点与点重合时如图1，易证（不需证明）‎ ‎（2）直线绕点逆时针方向旋转，当时，如图2、图3的位置，猜想线段之间有怎样的数量关系？请写出你对图2、图3的猜想，并选择一种情况给予证明．‎ 6‎ 例4;（2016攀枝花）如图，抛物线与轴交于两点，点坐标为，与轴交于点 ‎（1）求抛物线的解析式；‎ ‎（2）点在抛物线位于第四象限的部分上运动，当四边形的面积最大时，求点的坐标和四边形的最大面积．‎ ‎（3）直线经过两点，点在抛物线位于轴左侧的部分上运动，直线经过点和点，是否存在直线，使得直线与轴围成的三角形和直线与轴围成的三角形相似？若存在，求出直线的解析式，若不存在，请说明理由．‎ 6‎ 三、中考预测 ‎（2017扬州）如图，已知正方形的边长为4，点是边上的一个动点，连接，过点作的垂线交于点，以 为边作正方形，顶点在线段上，对角线相交于点．‎ ‎（1）若，则　　；‎ ‎（2）①求证：点一定在△的外接圆上；‎ ‎②当点从点运动到点时，点也随之运动，求点经过的路径长；‎ ‎（3）在点从点到点的运动过程中，△的外接圆的圆心也随之运动，求该圆心到边的距离的最大值．‎ 四、反思总结 ‎1.本节课你复习了哪些内容？‎ ‎2.通过本节课的学习，你还有哪些困难？‎ 五、达标检测 6‎ ‎1.（2008辽宁）直线与轴、轴分别相交于两点，圆心的坐标为，与轴相切于点．若将沿轴向左移动，当与该直线相交时，横坐标为整数的点有 个．‎ ‎2.（2017•葫芦岛）如图，点，点，连接，点分别是的中点，在射线上有一动点．若△是直角三角形，则点的坐标是　 　．‎ ‎3.（2015滨州）如图,在轴的上方，直角绕原点按顺时针方向旋转.‎ 若的两边分别与函数、的图象交于两点，则大小的变化趋势为（ ）‎ O x y B A P A.逐渐变小 B.逐渐变大 C.时大时小 D.保持不变 ‎4.（2017•葫芦岛）如图，抛物线与轴、轴分别交于点三点，已知点，点，点是抛物线的顶点．‎ ‎（1）求抛物线的解析式及顶点的坐标；‎ ‎（2）如图1，抛物线的对称轴与轴交于点，第四象限的抛物线上有一点，将△沿直线折叠，使点的对应点落在抛物线的对称轴上，求点的坐标；‎ ‎（3）如图2，设交抛物线的对称轴于点，作直线，点是直线上的动点，点是平面内一点，当以点为顶点的四边形是菱形时，请直接写出点的坐标．‎ 6‎ ‎5.（2016苏州）如图，在矩形中，，，点从点出发，沿对角线向点匀速运动，速度为，过点作交于点，以为一边作正方形，使得点落在射线上，点从点出发，沿向点匀速运动，速度为，以为圆心，为半径作⊙，点与点同时出发，设它们的运动时间为（单位：）（）．‎ ‎（1）如图1，连接平分时，的值为　　　　　　；‎ ‎（2）如图2，连接，若△是以为底的等腰三角形，求的值；‎ ‎（3）请你继续进行探究，并解答下列问题：‎ ‎①证明：在运动过程中，点始终在所在直线的左侧；‎ ‎②如图3，在运动过程中，当与⊙相切时，求的值；并判断此时与⊙是否也相切？说明理由．‎ 6‎ 6‎