中考数学分类汇编动点问题含答案 7页

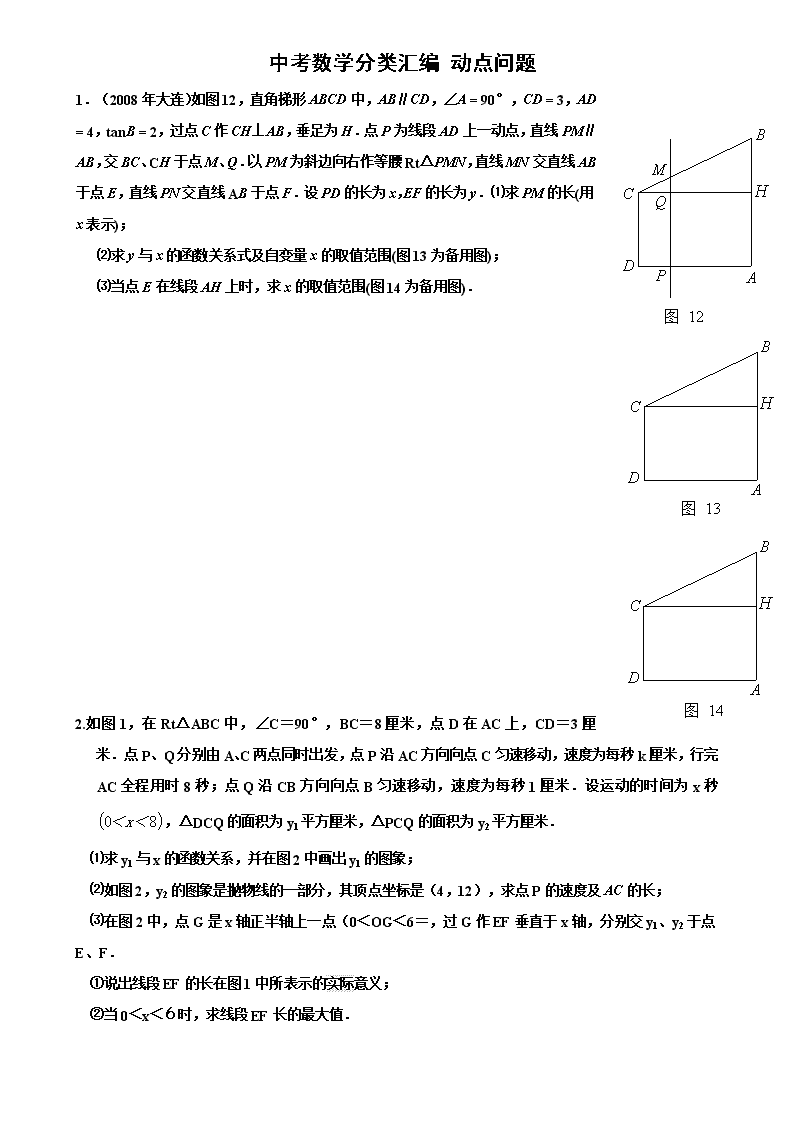
‎ 中考数学分类汇编 动点问题 ‎1．（2008年大连）如图12，直角梯形ABCD中，AB∥CD，∠A = 90°，CD = 3，AD = 4，tanB = 2，过点C作CH⊥AB，垂足为H．点P为线段AD上一动点，直线PM∥AB，交BC、CH于点M、Q．以PM为斜边向右作等腰Rt△PMN，直线MN交直线AB于点E，直线PN交直线AB于点F．设PD的长为x，EF的长为y．⑴求PM的长(用x表示)；‎ ‎⑵求y与x的函数关系式及自变量x的取值范围(图13为备用图)；‎ ‎⑶当点E在线段AH上时，求x的取值范围(图14为备用图)． ‎ ‎2.如图1，在Rt△ABC中，∠C＝90°，BC＝8厘米，点D在AC上，CD＝3厘米．点P、Q分别由A、C两点同时出发，点P沿AC方向向点C匀速移动，速度为每秒k厘米，行完AC全程用时8秒；点Q沿CB方向向点B匀速移动，速度为每秒1厘米．设运动的时间为x秒，△DCQ的面积为y1平方厘米，△PCQ的面积为y2平方厘米．‎ ‎⑴求y1与x的函数关系，并在图2中画出y1的图象；‎ ‎⑵如图2，y2的图象是抛物线的一部分，其顶点坐标是（4，12），求点P的速度及AC的长；‎ ‎⑶在图2中，点G是x轴正半轴上一点（0＜OG＜6＝，过G作EF垂直于x轴，分别交y1、y2于点E、F．‎ ‎①说出线段EF的长在图1中所表示的实际意义；‎ ‎②当0＜x＜６时，求线段EF长的最大值．‎ 图1‎ C Q→ B D A P↓‎ 图2‎ G ‎2 4 6 8 10 ‎ ‎1210‎ ‎8‎ ‎6‎ ‎4‎ ‎2‎ y O x ‎3.如图，在平面直角坐标系中，四边形OABC是矩形，点B的坐标为（4，3）．平行于对角线AC的直线m从原点O出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线m与矩形OABC的两边分别交于点M、N，直线m运动的时间为t（秒）．‎ ‎(1) 点A的坐标是__________，点C的坐标是__________；‎ ‎ (2) 当t= 秒或 秒时，MN=AC；‎ ‎(3) 设△OMN的面积为S，求S与t的函数关系式；‎ ‎(4) 探求(3)中得到的函数S有没有最大值？若有，求出最大值；若没有，要说明理由．‎ 针对练习 一、选择题：‎ ‎1. 如图，在矩形ABCD中，动点P从点B出发，沿BC、CD、DA运动至点A停止，设点P运动的路程为x，△ABP的面积为y，如果y关于x的函数图象如图2所示，则△ABC的面积是（ ）‎ ‎ ‎ ‎ A、10 B、16 C、18 D、20‎ 二、填空题：‎ ‎1. 如上右图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ.以下五个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°.‎ 恒成立的结论有_______________________（把你认为正确的序号都填上）。‎ 参考答案 一、选择 A 二、填空：（1）（2）（3）（5）‎ 三、解答：‎ ‎2、解：⑴∵，CD＝3，CQ＝x，‎ ‎∴．‎ 图象如图所示．‎ ‎⑵方法一：，CP＝8k－xk，CQ＝x，‎ E G ‎2 4 6 8 10 ‎ ‎1210‎ ‎8‎ ‎6‎ ‎4‎ ‎2‎ y O x F ‎∴．‎ ‎∵抛物线顶点坐标是（4，12），‎ ‎∴．‎ 解得．‎ 则点P的速度每秒厘米，AC＝12厘米．‎ 方法二：观察图象知，当x=4时，△PCQ面积为12．‎ 此时PC＝AC－AP＝8k－4k＝4k，CQ＝4．‎ ‎∴由，得 ．解得．‎ 则点P的速度每秒厘米，AC＝12厘米．‎ 方法三：设y2的图象所在抛物线的解析式是．‎ ‎∵图象过（0，0），（4，12），（8，0），‎ ‎∴ 解得 ‎ ‎∴． ①‎ ‎∵，CP＝8k－xk，CQ＝x，‎ ‎∴． ②‎ 比较①②得.‎ 则点P的速度每秒厘米，AC＝12厘米．‎ ‎⑶①观察图象，知 线段的长EF＝y2－y1，表示△PCQ与△DCQ的面积差（或△PDQ面积）．‎ ‎②由⑵得 .（方法二，）‎ ‎∵EF＝y2－y1，‎ ‎∴EF＝，‎ ‎∵二次项系数小于０，‎ ‎∴在范围，当时，最大．‎ ‎3、解：(1)（4，0），（0，3）； 2分 ‎(2) 2，6； 4分 ‎(3) 当0＜t≤4时，OM=t．‎ 由△OMN∽△OAC，得，‎ ‎∴ ON=，S=． 6分 当4＜t＜8时，‎ 如图，∵ OD=t，∴ AD= t-4． ‎ 方法一：‎ 由△DAM∽△AOC，可得AM=，∴ BM=6-． 7分 由△BMN∽△BAC，可得BN==8-t，∴ CN=t-4． 8分 S=矩形OABC的面积-Rt△OAM的面积- Rt△MBN的面积- Rt△NCO的面积 ‎=12--（8-t）（6-）-‎ ‎=． 10分 方法二：‎ 易知四边形ADNC是平行四边形，∴ CN=AD=t-4，BN=8-t． 7分 由△BMN∽△BAC，可得BM==6-，∴ AM=． 8分 以下同方法一．‎ ‎ (4) 有最大值．‎ 方法一：‎ 当0＜t≤4时，‎ ‎∵ 抛物线S=的开口向上，在对称轴t=0的右边， S随t的增大而增大，‎ ‎∴ 当t=4时，S可取到最大值=6； 11分 当4＜t＜8时，‎ ‎∵ 抛物线S=的开口向下，它的顶点是（4，6），∴ S＜6． ‎ 综上，当t=4时，S有最大值6． 12分 方法二：‎ ‎∵ S= ‎ ‎∴ 当0＜t＜8时，画出S与t的函数关系图像，如图所示． 11分 显然，当t=4时，S有最大值6． 12分 说明：只有当第（3）问解答正确时，第（4）问只回答“有最大值”无其它步骤，可给1分；否则，不给分．‎