深圳市历年中考数学试题及答案排好版 56页

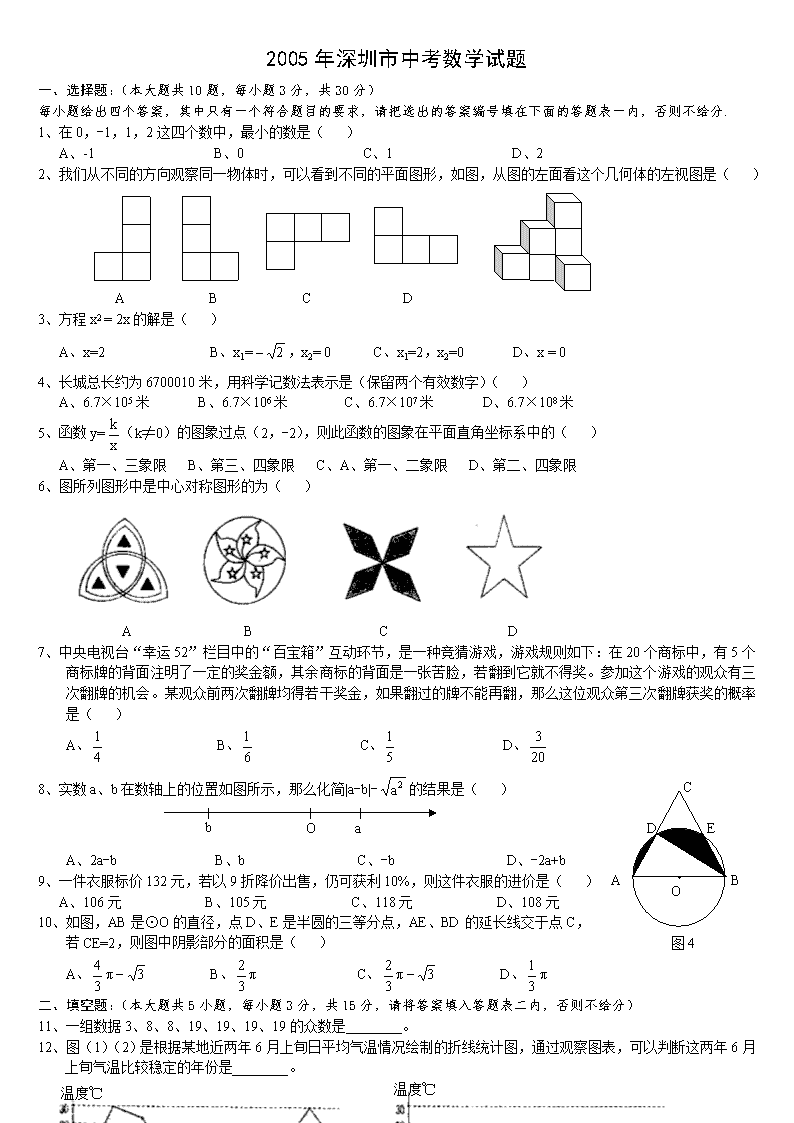
2005 年深圳市中考数学试题 一、选择题：（本大题共 10 题，每小题 3 分，共 30 分） 每小题给出四个答案，其中只有一个符合题目的要求，请把选出的答案编号填在下面的答题表一内，否则不给分. 1、在 0，-1，1，2 这四个数中，最小的数是（ ） A、-1 B、0 C、1 D、2 2、我们从不同的方向观察同一物体时，可以看到不同的平面图形，如图，从图的左面看这个几何体的左视图是（ ） A B C D 3、方程 x2 = 2x 的解是（ ） A、x=2 B、x1= ，x2= 0 C、x1=2，x2=0 D、x = 0 4、长城总长约为 6700010 米，用科学记数法表示是（保留两个有效数字）（ ） A、6.7×105 米 B、6.7×106 米 C、6.7×107 米 D、6.7×108 米 5、函数 y= （k≠0）的图象过点（2，-2），则此函数的图象在平面直角坐标系中的（ ） A、第一、三象限 B、第三、四象限 C、A、第一、二象限 D、第二、四象限 6、图所列图形中是中心对称图形的为（ ） A B C D 7、中央电视台“幸运 52”栏目中的“百宝箱”互动环节，是一种竞猜游戏，游戏规则如下：在 20 个商标中，有 5 个 商标牌的背面注明了一定的奖金额，其余商标的背面是一张苦脸，若翻到它就不得奖。参加这个游戏的观众有三 次翻牌的机会。某观众前两次翻牌均得若干奖金，如果翻过的牌不能再翻，那么这位观众第三次翻牌获奖的概率 是（ ） A、 B、 C、 D、 8、实数 a、b 在数轴上的位置如图所示，那么化简|a-b|- 的结果是（ ） A、2a-b B、b C、-b D、-2a+b 9、一件衣服标价 132 元，若以 9 折降价出售，仍可获利 10%，则这件衣服的进价是（ ） A、106 元 B、105 元 C、118 元 D、108 元 10、如图，AB 是⊙O 的直径，点 D、E 是半圆的三等分点，AE、BD 的延长线交于点 C， 若 CE=2，则图中阴影部分的面积是（ ） A、 B、 C、 D、 二、填空题：（本大题共 5 小题，每小题 3 分，共 15 分，请将答案填入答题表二内，否则不给分） 11、一组数据 3、8、8、19、19、19、19 的众数是________。 12、图（1）（2）是根据某地近两年 6 月上旬日平均气温情况绘制的折线统计图，通过观察图表，可以判断这两年 6 月 上旬气温比较稳定的年份是________。 2− x k 4 1 6 1 5 1 20 3 2a 33 4 −π π 3 2 33 2 −π π 3 1 b O a 温度℃ 温度℃ （1）2004 年 6 月上旬 （2）2005 年 6 月上旬 C ED O BA 图 4 13、如图，已知，在△ABC 和△DCB 中，AC=DB，若不增加任何字母与辅助线，要使△ABC≌△DCB，则还需增加 一个条件是________。 14、已知： ， ， ，……，若 （a、b 都是正整数），则 a+b 的最小 值是________。 （13） （15） 15、如图，口 ABCD 中，点 E 在边 AD 上，以 BE 为折痕，将△ABE 向上翻折，点 A 正好落在 CD 上的点 F，若△FDE 的周长为 8，△FCB 的周长为 22，则 FC 的长为________。 三、解答题：（共 7 题，共 55 分） 16、（6 分）计算：( )0+( )-1- -|-1| 17、（6 分）先化简，再求值：（ ）÷ ，其中 x=2005 18、（8 分）大楼 AD 的高为 10 米，远处有一塔 BC，某人在楼底 A 处测得踏顶 B 处的仰角 为 60º，爬到楼顶 D 点测得塔顶 B 点的仰角为 30º，求塔 BC 的高度。 19、（8 分）右图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图。 （1）求该班有多少名学生？ （2）补上步行分布直方图的空缺部分； （3）在扇形统计图中，求骑车人数所占的圆心角度数。 （4）若全年级有 500 人，估计该年级步行人数。 21 221 2 +=× 32 332 3 +=× 43 443 4 +=× 10b a10b a +=× 13 − 3 1 2)5(− 2x x 2x x +−− 2x x4 − A D B C D A B C E F 20 12 8 乘车 步行 骑车 步行 50% 步行 20% 骑车 30% D A C B 20、某工程，甲工程队单独做 40 天完成，若乙工程队单独做 30 天后，甲、乙两工程队再合作 20 天完成。 （1）（5 分）求乙工程队单独做需要多少天完成？ （2）（4 分）将工程分两部分，甲做其中一部分用了 x 天，乙做另一部分用了 y 天，其中 x、y 均为正整数，且 x<15，y<70，求 x、y. 21、已知△ABC 是边长为 4 的等边三角形，BC 在 x 轴上，点 D 为 BC 的中点，点 A 在第一象限内，AB 与 y 轴的正 半轴相交于点 E，点 B（-1，0），P 是 AC 上的一个动点（P 与点 A、C 不重合） （1）（2 分）求点 A、E 的坐标； （2）（2 分）若 y= 过点 A、E，求抛物线的解析式。 （3）（5 分）连结 PB、PD，设 L 为△PBD 的周长，当 L 取最小值时，求点 P 的坐标及 L 的最小值，并判断此时 点 P 是否在（2）中所求的抛物线上，请充分说明你的判断理由。 cbxx7 36 2 ++− A B CO D E y x 22、（9 分）AB 是⊙O 的直径，点 E 是半圆上一动点（点 E 与点 A、B 都不重合），点 C 是 BE 延长线上的一点，且 CD ⊥AB，垂足为 D，CD 与 AE 交于点 H，点 H 与点 A 不重合。 （1）（5 分）求证：△AHD∽△CBD （2）（4 分）连 HB，若 CD=AB=2，求 HD+HO 的值。 参考答案 一、选择题： ABCBD CBCDA 二、填空题： 11、19 12、2005 年 13、AB=DC 14、19 15、7 三、解答题： 16、解: 原式=1+3-5-1= -2 A O D B H E C 17、解：原式= · = = 18、解：作 BE⊥AD 的延长线于点 E 设 ED= x 在 Rt△BDE 中，BE= DE= 在 Rt△ABE 中，AE= BE=3x 由 AE-ED=AD 得：3x-x=10 解之得：x=5 所以 BC=5+10=15 答：塔 BC 的高度为 15 米。 19、解：（1）40 人 （2）见直方图 （3）圆心角度数= =108º （4）估计该年级步行人数=500×20%=100 20、解：（1）设乙工程队单独做需要 x 天完成。 则 30× +20( )=1，解之得：x=100 经检验得 x=100 是所列方程的解，所以求乙工程队单独做需要 100 天完成。 （2）甲做其中一部分用了 x 天，乙做另一部分用了 y 天 所以 ，即：y=100 - ，又 x<15，y<70 所以 ，解之得：12  + ≤ 1 0 2 0 x x − ≤  + < 1 0 2 0 x x + ≥  − < 1 0 2 0 x x + >  − ≤ ( 0)ky kx = ≠ y kx k= − 3 6 6 − 3 2 2 6 + 3 6 6 ± 3 2 2 6 ± 2 2 1 9 3 m m m − =− + AB=BC=CD=DA A B C DO A B CD A B C D E F 三、解答题（本大题有 7 题，其中第 16、17 题各 6 分；第 18 题７分；第 19、20 题各８分；第 21、22 题各 10 分， 共 55 分） 16．（6 分）计算： 解：原式＝ 17．（6 分）解方程： 解： 18．（７分）如图 7，在梯形 ABCD 中，AD∥BC, ， ．（1）（３分）求证： 证明： （2）（４分）若 ，求梯形 ABCD 的面积． 解： 19．（8 分）某中学图书馆将图书分为自然科学、文学艺术、社会百科、数学四类.在“深圳读书月” 活动期间，为了解图书的借阅情况，图书管理员对本月各类图书的借阅量进行了统计，图 8-1 和图 8-2 是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图．请你根据 图表中提供的信息,解答以下问题: （1）(2 分)填充图 8-1 频率分布表中的空格． （2）(2 分)在图 8-2 中，将表示“自然科学”的部分补充完整． 得分 阅卷人 得分 阅卷人 得分 阅卷人 得分 阅卷人 频率分布表 图书种类 频数 频率 自然科学 400 0.20 文学艺术 1000 0.50 社会百科 500 0.25 数学 2 1 02 8 sin 45 2 (3.14 )π−− + − + − 2 113 3 x x x − = −− − ADDCAB == 120ADC∠ =  DCBD ⊥ 4AB = A D B C 800 600 1000 图 8-2 自然科学 文学艺术 社会百科　数学 借阅量/册 400 200 0 图书 图 8-1 别忘了 验根哦! （3）(2 分)若该学校打算采购一万册图书,请你估算“数学”类图书应采购多少册较合适？ （4）(2 分) 根据图表提供的信息，请你提出一条合理化的建议． 20．(8 分)工艺商场按标价销售某种工艺品时，每件可获利 45 元；按标价的八五折销售该工艺品 8 件与将标价降低 35 元销售该工艺品 12 件所获利润相等. （1）(4 分)该工艺品每件的进价、标价分别是多少元？ （2）(4 分)若每件工艺品按（1）中求得的进价进货，标价售出，工艺商场每天可售出该工艺品 100 件．若每件工艺品降价 1 元，则每天可多售出该工艺品 4 件．问每件工艺品降价多少元出售， 每天获得的利润最大？获得的最大利润是多少元? 21．(10 分)如图 9，抛物线 与 轴交于 、 两点（点 在点 的左 侧），抛物线上另有一点 在第一象限，满足∠ 为直角,且恰使△ ∽△ . (1)(3 分)求线段 的长. 解： (2)(3 分)求该抛物线的函数关系式． 解： (3)(4 分)在 轴上是否存在点 ，使△ 为等腰三角形？若存在，求 出所有符合条件的 点的坐标；若不存在，请说明理由. 解： 22．(10 分)如图 10-1，在平面直角坐标系 中，点 在 轴的正半轴上， ⊙ 交 轴于 两点，交 轴于 两点，且 为 的中点， 交 轴于 点，若点 的坐标为 （－2，0）， (1)(3 分)求点 的坐标. 解： (2)(3 分)连结 ，求证： ∥ 证明： 得分 阅卷人 得分 阅卷人 得分 阅卷人 2 8 12 ( 0)y ax ax a a= − + < x A B A B C ACB OCA OBC OC x P BCP P xoy M x M x A B、 y C D、 C AE AE y G A AE 8= C MG BC、 MG BC (3)(４分) 如图 10-2，过点 作⊙ 的切线，交 轴于点 .动点 在⊙ 的圆周上运动时， 的比值是否发生变 化，若不变，求出比值；若变化，说明变化规律. 解： 深圳市 2006 年初中毕业生学业考试数学试题 答案及评分意见 一、选择题（本大题共 10 小题，每小题 3 分，共 30 分） 题号 １ ２ ３ ４ ５ ６ ７ ８ ９ 10 答案 B C C D D A C B B A 二、填空题(本大题共 5 小题，每小题 3 分，共 15 分) 三、解答题（本大题有 7 题，其中第 16、17 题各 6 分；第 18 题７分；第 19、20 题各８分；第 21、22 题各 10 分， 共 55 分） 16.解:原式= 　　　　　……１＋１＋１＋１分 = 　　　　　　　　　　　……５分 = 　　　　　　　　　　　　　　　……６分 17.解:去分母: 　　　　　　　　……２分 化简得: 　　　　　　　　　　　　　……４分 经检验，原分式方程的根是： .　　　　……６分 18. （1） 证明： AD∥BC， ， 　　　　　　……1 分 又 答题表一 题号 11 12 13 14 15 答案 或 或 ……等等 55 7 D M x P F M PF OF 2 14 2 2 12 2 − + ⋅ − + 14 2 12 − + − + 3 2 − (2 ) 3 1x x− = − + 2 4x = 2x = 2x =  120=∠ADC ∴ 60=∠C  ADDCAB == 1 3 1 3m − AC BD= AB BC⊥ oABD=45∠ A D B C E ， ……2 分 ， 　 …… 3 分 （2）解：过 D 作 于 E, 在 Rt 中， , , （１分） 在 Rt 中， （２分） （４分） 19. （1）（频数）100，（频率）0.05　　　　　　　 ……２分 （2）补全频率分布直方图（略）　　　　　　　 ……４分 (3) 10000×0.05=500 册　 　　　　　　　 ……6 分 (4) 符合要求即可. ……8 分 20. (1) 解.设该工艺品每件的进价是 元,标价是 元.依题意得方程组: 　　 　 　……2 分 解得：　 　……3 分 答：该工艺品每件的进价是 155 元，标价是 200 元. 　……4 分 (2) 解: 设每件应降价 元出售,每天获得的利润为 元. 依题意可得 W 与 的函数关系式: 　……2 分 配方得: 当 时, =4900 　……3 分 答:每件应降价 10 元出售,每天获得的利润最大,最大利润是 4900 元. 　……4 分 21．（１）解：由 ax －8ax+12a＝０（a＜0）得 　　　 ｘ ＝２，ｘ ＝６ 　　　即：ＯＡ＝２，ＯＢ＝６ 　……1 分 　　　∵△OCA∽△OBC 　　　∴ＯＣ ＝ＯＡ·ＯＢ＝２×６ 　……2 分 ∴ 60=∠=∠ CABC 30=∠=∠=∠ DBCADBABD ∴ 90=∠BDC DCBD ⊥ BCDE ⊥ DEC∆  60=∠C 4AB DC= = ∴ 60sin= DC DE 2 3DE = BDC∆ 30sin= BC DC 2 8BC DC= = 1 ) 12 32S AD BC DE= + ⋅ =梯形 （ x y 45 8 0.85 8 ( 35) 12 12 y x y x y x − =  ⋅ − = − ⋅ − 155 200 x y =  = a W a (45 )(100 4 )W a a= − + 24 80 4500W a a= − + + 24( 10) 4900W a= − − + 10a = W最大 2 1 2 2 　　　∴ＯＣ＝２ （－２ 舍去） 　　　∴线段ＯＣ的长为２ 　　……3 分 （２）解：∵△OCA∽△OBC 　　　∴ 设ＡＣ＝ｋ，则ＢＣ＝ ｋ 由ＡＣ ＋ＢＣ ＝ＡＢ 得 ｋ ＋（ ｋ） ＝（６－２） 解得ｋ＝２（－２舍去） ∴ＡＣ＝２，ＢＣ＝２ ＝ＯＣ 　 ……1 分 过点Ｃ作ＣＤ⊥ＡＢ于点Ｄ ∴ＯＤ＝ ＯＢ＝３ ∴ＣＤ＝ ∴Ｃ的坐标为（３， ） 　 ……2 分 将 C 点的坐标代入抛物线的解析式得 ＝ａ（３－２）（３－６） ∴ａ＝－ ∴抛物线的函数关系式为： ｙ＝－ ｘ ＋ ｘ－４ 　　　　　　　　 ……3 分 （３）解：①当Ｐ 与Ｏ重合时，△ＢＣＰ 为等腰三角形 　　　　　　∴Ｐ 的坐标为（０，０） ……1 分 ②当Ｐ Ｂ＝ＢＣ时(Ｐ 在 B 点的左侧)，△ＢＣＰ 为等腰三角形 ∴Ｐ 的坐标为（６－２ ，０） ……2 分 ③当Ｐ 为ＡＢ的中点时，Ｐ Ｂ＝Ｐ Ｃ，△ＢＣＰ 为等腰三角形 ∴Ｐ 的坐标为（４，０） ……3 分 ④ 当ＢＰ ＝ＢＣ时(Ｐ 在 B 点的右侧)，△ＢＣＰ 为等腰三角形 ∴Ｐ 的坐标为（６＋２ ，０） 3 3 3 2 1 2 3 3 AC OA BC OC = = = 3 2 2 2 2 3 2 2 3 1 2 2 2 3OC OD− = 3 3 3 3 3 3 2 8 3 3 3 1 1 1 2 2 2 2 3 3 3 3 3 3 4 4 4 4 3 ∴在ｘ轴上存在点Ｐ，使△ＢＣＰ为等腰三角形，符合条件的点Ｐ的坐标为： （０，０），（６－２ ，０），（４，０），（６＋２ ，０） ……4 分 ２２．解（１）方法（一）∵直径ＡＢ⊥ＣＤ 　　　　　　　　∴ＣＯ＝ ＣＤ 　　……1 分 ＝ 　　　　　　　　∵Ｃ为 的中点 　　　　　　　　∴ ＝ 　　　　　　　　∴ ＝ 　　　　　　　　∴ＣＤ＝ＡＥ 　　　　……2 分 　　　　　　　　∴ＣＯ＝ ＣＤ＝４ 　　　　　　　　∴Ｃ点的坐标为（０，４） 　　　……3 分 　　　　　　方法（二）连接ＣＭ，交ＡＥ于点Ｎ 　　　　　　　　∵Ｃ为 的中点，Ｍ为圆心 　　　　　　　　∴ＡＮ＝ ＡＥ＝４ ……1 分 　　　　　　　　　ＣＭ⊥ＡＥ 　　　　　　　　∴∠ＡＮＭ＝∠ＣＯＭ＝９０° 　　　　　　　　在△ＡＮＭ和△ＣＯＭ中： ∴△ＡＮＭ≌△ＣＯＭ ……2 分 ∴ＣＯ＝ＡＮ＝４ ∴Ｃ点的坐标为（０，４） ……3 分 　　　　解（２）设半径ＡＭ＝ＣＭ＝ｒ，则ＯＭ＝ｒ－２ 　　　　　　　　由ＯＣ ＋ＯＭ ＝ＭＣ 得： 　　　　　　　　４ ＋（ｒ－２） ＝ｒ 　　　　　　　　解得：ｒ＝５ ……1 分 　　　　　　　　∵∠ＡＯＣ＝∠ＡＮＭ＝９０° 　　　　　　　　　∠ＥＡＭ＝∠ＭＡＥ 　　　　　　　　∴△ＡＯＧ∽△ＡＮＭ 　　　　　　　　∴ ∵ＭＮ＝ＯＭ＝３ 　　　　　　　　即 　　　　　　　　∴ＯＧ＝ 　　　　　　　　　　　　　　……２分 3 3 1 2 AD AC AE AC CE AE CD 1 2 AC 1 2 CMO AMN ANM COM AM CM ∠ = ∠ ∠ = ∠  = 2 2 2 2 2 2 OG AO MN AN = 2 3 4 OG = 3 2 　　　　　　　　∵ 　　　　　　　　　 　　　　　　　　∴ 　　　　　　　　∵∠ＢＯＣ＝∠ＢＯＣ 　　　　　　　　∴△ＧＯＭ∽△ＣＯＢ 　　　　　　　　∴∠ＧＭＯ＝∠ＣＢＯ 　　　　　　　　∴ＭＧ∥ＢＣ　　　　　　　　　　　　　……3 分 　　　　　　　　（说明：直接用平行线分线段成比例定理的逆定理不扣分） 　　　　　解（３）连结ＤＭ，则ＤＭ⊥ＰＤ，ＤＯ⊥ＰＭ 　　　　　　　　∴△ＭＯＤ∽△ＭＤＰ，△ＭＯＤ∽△ＤＯＰ 　　　　　　　　∴ＤＭ ＝ＭＯ·ＭＰ； 　　　　　　　　　ＤＯ ＝ＯＭ·ＯＰ（说明：直接使用射影定理不扣分） 　　　　　　　　即４ ＝３·ＯＰ 　　　　　　　　∴ＯＰ＝ 　　　　　　　　　　　 ……１分 　　　　　　　　当点Ｆ与点Ａ重合时： 　　　　　　　　当点Ｆ与点Ｂ重合时： 　　　……２分 　　　　　　　　当点Ｆ不与点Ａ、Ｂ重合时：连接ＯＦ、ＰＦ、ＭＦ 　　　　　　　　∵ＤＭ ＝ＭＯ·ＭＰ 　　　　　　　　∴ＦＭ ＝ＭＯ·ＭＰ 　　　　　　　　∴ 　　　　　　　　∵∠ＡＭＦ＝∠ＦＭＡ 　　　　　　　　∴△ＭＦＯ∽△ＭＰＦ 　　　　　　　　∴ 　　　　　　　　 　　　　　　　　∴综上所述， 的比值不变，比值为 ……4 分 说明：解答题中的其它解法，请参照给分。 1.5 3 4 8 OG OC = = 3 8 OM OB = OG OM OC OB = 2 2 2 16 3 2 3 16 523 OF AO PF AP = = = − 8 3 16 583 OF OB PF PB = = = + 2 2 FM MP OM FM = 3 5 OF MO PF MF = = OF PF 3 5 深圳市 2007 年初中毕业生学业考试 数学试卷 说明：1．全卷分二部分，第一部分为选择题，第二部分为非选择题，共 4 页．考试时间 90 分钟，满分 100 分． 2．本卷试题，考生必须在答题卡上按规定作答；凡在试卷、草稿纸上作答的，其答案一律无效．答题卡必须保持 清洁，不能折叠． 3．答题前，请将姓名、考生号、考场、试室号和座位号用规定的笔写在答题卡指定的位置上，将条形码粘贴 好． 4．本卷选择题 1－10，每小题选出答案后，用 2B 铅笔将答题卡选择题答题区内对应题目的答案标号涂黑，如需 改动，用橡皮擦干净后，再选涂其它答案；非选择题 11－23，答案（含作辅助线）必须用规定的笔，按作答题目序号， 写在答题卡非选择题答题区内． 5．考试结束，请将本试卷和答题卡一并交回． 第一部分　选择题 （本部分共 10 小题，每小题 3 分，共 30 分．每小题给出 4 个选项，其中只有一个是正确的） 1． 的相反数是（　　） Ａ． Ｂ． Ｃ． Ｄ． 2．今年参加我市初中毕业生学业考试的考生总数为 人，这个数据用科学记数法表示为（　　） Ａ． Ｂ． Ｃ． Ｄ． 3．仔细观察图 1 所示的两个物体，则它的俯视图是（　　） 4．下列图形中，不是轴对称图形的是（　　） 5．已知三角形的三边长分别是 ；若 的值为偶数，则 的值有（　　） Ａ． 个 Ｂ． 个 Ｃ． 个 Ｄ． 个 6．一件标价为 元的商品，若该商品按八折销售，则该商品的实际售价是（　　） Ａ． 元 Ｂ． 元 Ｃ． 元 Ｄ． 元 7．一组数据 ， ， ， ， 的方差是（　　） Ａ． Ｂ． Ｃ． Ｄ． 8．若 ，则 的值是（　　） Ａ． Ｂ． Ｃ． Ｄ． 9．如图 2，直线 ，则 的度数是（　　） Ａ． Ｂ． Ｃ． Ｄ． 10．在同一直角坐标系中，函数 与 的图象大致是（　　） 第二部分　非选择题 填空题（本题共 5 小题，每小题 3 分，共 15 分） 11．一个口袋中有 4 个白球，5 个红球，6 个黄球，每个球除颜色外都相同，搅匀后随机从袋中摸出一个球，这个球是 白球的概率是　　　　　． 2− 1 2 − 2− 1 2 2 45730 50.4573 10× 44.573 10× 44.573 10− × 34.573 10× 3 8 x，， x x 6 5 4 3 250 180 200 240 250 2− 1− 0 1 2 1 2 3 4 2( 2) 3 0a b− + + = 2007( )a b+ 0 1 1− 2007 a b∥ A∠ 28 31 39 42 ( 0)ky kx = ≠ ( 0)y kx k k= + ≠ 正面 图 1 Ａ ． Ｂ ． Ｃ ． Ｄ ． Ａ ． Ｂ ． Ｃ ． Ｄ ． A B C D a b 图 2 70° 31° Ａ． x y Ｂ． x y Ｃ． x y Ｄ． x y 12．分解因式： 　　　　　． 13．若单项式 与 是同类项，则 的值是　　　　　． 14．直角三角形斜边长是 ，以斜边的中点为圆心，斜边上的中线为半径的圆的面积是　　　　　． 15．邓老师设计了一个计算程序，输入和输出的数据如下表： 输入数据 1 2 3 4 5 6 … 输出数据 … 那么，当输入数据是 时，输出的数据是　　　　　． 解答题（本题共 8 小题，其中第 16 题 5 分，第 17 题 6 分，第 18 题 6 分，第 19 题 6 分，第 20 题 7 分，第 21 题 8 分， 第 22 题 9 分，第 23 题 8 分，共 55 分） 16．计算： 17．解不等式组，并把它的解集表示在数轴上： 18．如图 3，在梯形 中， ， ， 是 上一点， ， ． （1）求证： ． （2）若 ，求 的长． 19．2007 年某市国际车展期间，某公司对参观本次车展盛会的消费者进行了随机问卷调查，共发放 1000 份调查问卷， 并全部收回．①根据调查问卷的结果，将消费者年收入的情况整理后，制成表格如下： 年收入（万元） 4.8 6 7.2 9 10 被调查的消费者人数（人） 200 500 200 70 30 ②将消费者打算购买小车的情况整理后，作出频数分布直方图的一部分（如图 4）． 注：每组包含最小值不包含最大值，且车价取整数．请你根据以上信息，回答下列问题． （1）根据①中信息可得，被调查消费者的年收入的众数是______万元． （2）请在图 4 中补全这个频数分布直方图． （3）打算购买价格 万元以下小车的消费者人数占被调查消费者人数的百分比是______． 22 4 2x x− + 22 mx y 31 3 nx y− m n+ 6 1 2 2 7 3 14 4 23 5 34 6 47 7 0 1 π3 2 sin 45 2007 3 −  − + −    2( 2) 3 1 3 4 x x x x + + +< ≤ ① ② ABCD AD BC∥ EA AD⊥ M AE BAE MCE=∠ ∠ 45MBE = ∠ BE ME= 7AB = MC 10 图 3 A B C D M E 图 4 0 4 6 8 10 12 14 16 车价/万元 人数/人 40 120 200 360 20．如图 5，某货船以 海里／时的速度将一批重要物资从 处运往正东方向的 处，在点 处测得某岛 在北偏 东 的方向上．该货船航行 分钟后到达 处，此时再测得该岛在北偏东 的方向上，已知在 岛周围 海里的 区域内有暗礁．若继续向正东方向航行，该货船有无触礁危险？试说明理由． 21． 两地相距 公里，甲工程队要在 两地间铺设一条输送天然气管道，乙工程队要在 两地间铺设 一条输油管道．已知甲工程队每周比乙工程队少铺设 公里，甲工程队提前 周开工，结果两队同时完成任务，求甲、 乙两工程队每周各铺设多少公里管道？ 22．如图 6，在平面直角坐标系中，正方形 的边长为 ，点 在 轴的正半轴上，且 ， 交 于 点 ． （1）求 的度数． （2）求点 的坐标． （3）求过 三点的抛物线的解析式．（计算结果要求分母有理化．参考资料：把分母中的根号化去，叫分母 有理化．例如：① ； ② ；③ 等运算都是分母有理化） 23．如图 7，在平面直角坐标系中，抛物线 与直线 相交于 两点． （1）求线段 的长． （2）若一个扇形的周长等于（1）中线段 的长，当扇形的半径取何值时，扇形的面积最大，最大面积是多少？ （3）如图 8，线段 的垂直平分线分别交 轴、 轴于 两点，垂足为点 ，分别求出 的长， 并验证等式 是否成立． 24 A M A C 60 30 B 30 C 9 A B， 18 A B， A B， 1 3 AOCB 1 D x OD OB= BD OC E BEC∠ E B O D， ， 2 2 5 2 5 55 5 5 = =  1 1 ( 2 1) 2 1 2 1 ( 2 1)( 2 1) × += = + − − + 1 5 3 5 3 23 5 ( 5 3)( 5 3) − −= = + + − 21 64y x= − 1 2y x= A B， AB AB AB x y C D， M OM OC OD， ， 2 2 2 1 1 1 OC OD OM + = 图 5 北 60° 30° A B C M A B C 图 6 O E D y x A B O y x 图 7 A B O y x 图 8 C D M （4）如图 9，在 中， ， ，垂足为 ，设 ， ， ． ， 试说明： ． 深圳市 2007 年初中毕业生学业考试数学试卷 参考答案 第一部分 选择题（本题共 10 小题，每小题 3 分，共 30 分） 题号 1 2 3 4 5 6 7 8 9 10 答案 D B A A D B B C C C 第二部分 非选择题 填空题（本题共 5 小题，每小题 3 分，共 15 分） 题号 11 12 13 14 15 答案 解答题（本题共 7 小题，其中第 16 题 5 分，第 17 题 6 分，第 18 题 6 分，第 19 题 6 分，第 20 题 7 分，第 21 题 8 分， 第 22 题 9 分，第 23 题 8 分，共 55 分） 16． 17．原不等式组的解集为 ≤ 18．(1)证明略 (2)∴MC＝7 19．(1) 6 (2)略 (3) 20． ∵ 所以货船继续向正东方向行驶无触礁危险． 21．设甲工程队每周铺设管道 公里,则乙工程队每周铺设管道( )公里 根据题意, 得 解得 ， 经检验 ， 都是原方程的根 Rt ABC△ 90ACB = ∠ CD AB⊥ D BC a= AC b= AB c= CD b= 2 2 2 1 1 1 a b h + = 15 4 2)1(2 −x 5 π9 62 7 3 1 x 1− %52%1001000 36012040 =×++ 936 > x 1+x 31 1818 =+− xx 21 =x 32 −=x 21 =x 32 −=x 图 9 A B C D ab c h 但 不符合题意,舍去 ∴ 答: 甲工程队每周铺设管道 2 公里,则乙工程队每周铺设管道 3 公里． 22．(1）∴ ∴ （2）点 E 的坐标是 ， ） （3）设过 B、O、D 三点的抛物线的解析式为 ∵B（-1，1），O（0，0），D（ ，0） ∴ 解得， 所以所求的抛物线的解析式为 23．（1） ∴A（-4，-2），B（6，3） 分别过 A、B 两点作 轴， 轴，垂足分别为 E、F ∴AB=OA+OB （2）设扇形的半径为 ，则弧长为 ，扇形的面积为 则 ∵ ∴当 时，函数有最大值 （3）过点 A 作 AE⊥ 轴，垂足为点 E ∵CD 垂直平分 AB，点 M 为垂足 ∴ ∵ ∴△AEO∽△CMO 32 −=x 31 =+x  5.22452 1 2 1 =×=∠=∠=∠ OBCOBDCBE  5.675.229090 =−=∠−=∠ CBEBEC 0( 22 − cbxaxy ++= 2 2 1=+− cba 0=c 022 =++ cba 0,22,21 =+−=+−= cba xxy )22()21( 2 +−++−= xAE ⊥ yBF ⊥ 2222 3624 +++= 55= x )255( x− y )255(2 1 xxy −= xx 52 52 +−= 16 125)4 55( 2 +−−= x 01 <−=a 4 55=x 16 125=最大y x 2 5522 55 2 1 =−=−= OAABOM COMEOAOMCAEO ∠=∠∠=∠ , ∴ ∴ ∴ 同理可得 ∴ ∴ ∴ （4）等式 成立．理由如下： ∵ ∴ ∴ ∴ ∴ ∴ ∴ ∴ ∴ CO AO OM OE = CO 52 2 5 4 = 4 5 4 1522 5 =⋅⋅=CO 2 5=OD 5 4 25 20)5 2()5 4(11 22 22 ==+=+ ODOC 5 41 2 = OM 222 111 OMODOC =+ 222 111 hba =+ ABCDACB ⊥=∠ ,90 222 2 1 2 1 baABhABab +=⋅= hcab ⋅= 2222 hcba ⋅= 22222 )( hbaba += 222 222 222 22 )( hba hba hba ba += 22 22 2 1 ba ba h += 222 111 bah += 222 111 hba =+ 深圳市 2008 年初中毕业生学业考试 数学试卷 说明：1、全卷分二部分，第一部分为选择题，第二部分为非选择题，共 4 页。考试时间 90 分钟，满分 100 分。 2、本卷试题，考生必须在答题卡上按规定作答；凡在试卷、草稿纸上作答的，其答案一律无效。答题卡必须保 持清洁，不能折叠。 3、答题前，请将姓名、考生号、考场、试室号和座位号用规定的笔写在答题卡指定的位置上，将条形码粘贴好。 4、本卷选择题 1—10，每小题选出答案后，用 2B 铅笔将答题卡选择题答题区内对应题目的答案标号涂黑，如需 改动，用橡皮擦干净后，再选涂其它答案；非选择题 11—22，答案（含作辅助线）必须用规定的笔，按作答 题目序号，写在答题卡非选择题答题区内。 5、考试结束，请将本试卷和答题卡一并交回。 第一部分 选择题 （本部分共 10 小题，每小题 3 分，共 30 分．每小题给出 4 个选项，其中只有一个是正确的） 1．4 的算术平方根是 Ａ．－4 Ｂ．4　 　 　Ｃ．－2　　　　 Ｄ．2 2．下列运算正确的是 Ａ． Ｂ． 　　 Ｃ． 　　　Ｄ． ÷ 3．2008 年北京奥运会全球共选拔 21880 名火炬手，创历史记录．将这个数据精确到千位， 用科学记数法表示为 Ａ． 　 　Ｂ． Ｃ． 　　 Ｄ． 4．如图１，圆柱的左视图是 图１　　　　 Ａ　　　　 　 Ｂ　　　　 　Ｃ　　 　 　Ｄ 5．下列图形中，既是轴对称图形又是中心对称图形的是 Ａ　　 　　 　 　Ｂ　　　　 　　　 Ｃ　　　　　 　　Ｄ 6．某班抽取 6 名同学参加体能测试，成绩如下:80，90，75，75，80，80.下列表述错误的是 Ａ．众数是 80 Ｂ．中位数是 75 Ｃ．平均数是 80 Ｄ．极差是 15 7．今年财政部将证券交易印花税税率由 3‰调整为 1‰（1‰表示千分之一）．某人在调整后购买 100000 元股票，则比 调整前少交证券交易印花税多少元？ 532 aaa =+ 532 aaa =⋅ 532 )( aa = 10a 52 aa = 31022× 5102.2 × 4102.2 × 51022.0 × Ａ．200 元 Ｂ．2000 元 Ｃ．100 元 Ｄ．1000 元 8．下列命题中错误的是 　　Ａ．平行四边形的对边相等　 Ｂ．两组对边分别相等的四边形是平行四边形　　　 Ｃ．矩形的对角线相等　　　 Ｄ．对角线相等的四边形是矩形 　 9．将二次函数 的图象向右平移 1 个单位，再向上平移 2 个单位后，所得图象的函数表 达式是 Ａ． Ｂ． Ｃ． Ｄ． 10．如图 2，边长为 1 的菱形 ABCD 绕点 A 旋转，当 B、C 两点 恰好落在扇形 AEF 的弧 EF 上时，弧 BC 的长度等于 Ａ． 　　　Ｂ． Ｃ． 　　　Ｄ． 　　 第二部分 非选择题 填空题（本题共 5 小题，每小题 3 分，共 15 分） 11．有 5 张质地相同的卡片，它们的背面都相同，正面分别印有“贝贝”、“晶晶”、“欢欢”、“迎迎”、“妮妮”五种不 同形象的福娃图片．现将它们背面朝上，卡片洗匀后，任抽一张是“欢欢”的概率是 12．分解因式： 13．如图 3，直线 OA 与反比例函数 的图象在第一象限交于 A 点，AB⊥x 轴于 点 B，△OAB 的面积为 2，则 k＝ 14．要在街道旁修建一个奶站，向居民区 A、B 提供牛奶，奶站应建在什么地方，才能使从 A、 B 到它的距离之和最短？小聪根据实际情况，以街道旁为 x 轴，建立了如图 4 所示的平面 直角坐标系，测得 A 点的坐标为（0，3），B 点的坐标为（6，5），则从 A、B 两点到奶站 距离之和的最小值是 15．观察表一，寻找规律．表二、表三分别是从表一中选取的一部分，则 a+b 的值为 表一 表二 表三 解答题（本题共 7 小题，其中第 16 题 6 分，第 17 题 7 分，第 18 题 7 分，第 19 题 8 分，第 20 题 8 分，第 21 题 9 分， 第 22 题 10 分，共 55 分） 16．计算： 17．先化简代数式 ÷ ，然后选取一个合适的 a 值，代入求值． 0 1 2 3 … 1 3 5 7 … 2 5 8 11 … 3 7 11 15 … … … … … … 11 14 a 11 13 17 b 2xy = 2)1( 2 +−= xy 2)1( 2 ++= xy 2)1( 2 −−= xy 2)1( 2 −+= xy 6 π 4 π 3 π 2 π =− aax 42 )0( ≠= kx ky 03 )2008(830tan33 π−−−°⋅+−      −++ 2 2 2 aa a 4 1 2 −a 图 2 FE D CB A 图 3 图 5 E D C BA 18．如图 5，在梯形 ABCD 中，AB∥DC， DB 平分∠ADC，过点 A 作 AE∥BD，交 CD 的 延长线于点 E，且∠C＝2∠E． （1）求证：梯形 ABCD 是等腰梯形． （2）若∠BDC＝30°，AD＝5，求 CD 的长． 19．某商场对今年端午节这天销售 A、B、C 三种品牌粽子的情况进行了统计，绘制如图 6 和 图 7 所示的统计图．根据图中信息解答下列问题： （1）哪一种品牌粽子的销售量最大？ （2）补全图 6 中的条形统计图． （3）写出 A 品牌粽子在图 7 中所对应的圆心角的度数． （4）根据上述统计信息，明年端午节期间该商场对 A、B、C 三种品牌的粽子如何进货？ 请你提一条合理化的建议． 20． 21．“震灾无情人有情”．民政局将全市为四川受灾地区捐赠的物资打包成件，其中帐篷和食 品共 320 件，帐篷比食品多 80 件． （1）求打包成件的帐篷和食品各多少件？ （2）现计划租用甲、乙两种货车共 8 辆，一次性将这批帐篷和食品全部运往受灾地区．已知甲种货车最多可装帐 篷 40 件和食品 10 件，乙种货车最多可装帐篷和食品各 20 件．则民政局安排甲、乙两种货车时有几种方案？请你 帮助设计出来． （3）在第（2）问的条件下，如果甲种货车每辆需付运输费 4000 元，乙种货车每辆需付运输费 3600 元．民政局应 选择哪种方案可使运输费最少？最少运输费是多少元？ 22．如图 9，在平面直角坐标系中，二次函数 的图象的顶点为 D 点， 与 y 轴交于 C 点，与 x 轴交于 A、B 两点， A 点在原点的左侧，B 点的坐标为（3，0）， OB＝OC ，tan∠ACO＝ ． （1）求这个二次函数的表达式． （2）经过 C、D 两点的直线，与 x 轴交于点 E，在该抛物线上是否存在这样的点 F，使以点 A、C、E、F 为顶点的 四边形为平行四边形？若存在，请求出点 F 的坐标；若不存在，请说明理由． （3）若平行于 x 轴的直线与该抛物线交于 M、N 两点，且以 MN 为直径的圆与 x 轴相切，求该圆半径的长度． （4）如图 10，若点 G（2，y）是该抛物线上一点，点 P 是直线 AG 下方的抛物线上一动点，当点 P 运动到什么位 置时，△APG 的面积最大？求出此时 P 点的坐标和△APG 的最大面积. )0(2 >++= acbxaxy 3 1 图 7 C品牌 50% 深圳市 2008 年初中毕业生学业考试 数学试卷 参考答案及评分意见 第一部分 选择题（本题共 10 小题，每小题 3 分，共 30 分） 题号 1 2 3 4 5 6 7 8 9 10 答案 D B C C B B A D A C 第二部分 非选择题 填空题（本题共 5 小题，每小题 3 分，共 15 分） 题号 11 12 13 14 15 答案 4 10 37 解答题（本题共 7 小题，其中第 16 题 6 分，第 17 题 7 分，第 18 题 7 分，第 19 题 8 分，第 20 题 8 分， 第 21 题 9 分，第 22 题 10 分，共 55 分） 16．解:　原式＝ …………………1+1+1+1 分 　　＝ …………………………5 分 ＝1 …………………………6 分 （注：只写后两步也给满分.） 17．解: 方法一： 原式＝ ＝ ＝ …………………………5 分 （注：分步给分，化简正确给 5 分．） 5 1 )2)(2( −+ xxa 123 333 −−⋅+ 1213 −−+ 4 1 )2)(2( )2(2 )2)(2( )2( 2 −÷    −+ ++−+ − aaa a aa aa )2)(2()2)(2( 42 −+−+ + aaaa a 42 +a 方法二：原式＝ ＝ ＝ …………………………5 分 取 a＝1，得 …………………………6 分 原式＝5 …………………………7 分 （注：答案不唯一．如果求值这一步，取 a＝2 或－2，则不给分．） 18．（1）证明：∵AE∥BD, ∴∠E＝∠BDC ∵DB 平分∠ADC ∴∠ADC＝2∠BDC 又∵∠C＝2∠E ∴∠ADC＝∠BCD ∴梯形 ABCD 是等腰梯形 …………………………3 分 （2）解：由第（1）问，得∠C＝2∠E＝2∠BDC＝60°，且 BC＝AD＝5 ∵ 在△BCD 中，∠C＝60°, ∠BDC＝30° ∴∠DBC＝90° ∴DC＝2BC＝10 …………………………7 分 19．解: （1）C 品牌．（不带单位不扣分） …………………………2 分 （2）略．（B 品牌的销售量是 800 个，柱状图上没有标数字不扣分） ……4 分 （3）60°．（不带单位不扣分） …………………………6 分 （4）略．（合理的解释都给分） …………………………8 分 20． 21．解：（1）设打包成件的帐篷有 x 件，则 （或 ） …………………………2 分 解得 ， …………………………3 分 答：打包成件的帐篷和食品分别为 200 件和 120 件． …………………………3 分 方法二：设打包成件的帐篷有 x 件，食品有 y 件，则 …………………………2 分 解得 …………………………3 分 答：打包成件的帐篷和食品分别为 200 件和 120 件． …………………………3 分 （注：用算术方法做也给满分．） （2）设租用甲种货车 x 辆，则 …………………………4 分 解得 …………………………5 分 ∴x＝2 或 3 或 4，民政局安排甲、乙两种货车时有 3 种方案． 设计方案分别为：①甲车 2 辆，乙车 6 辆； )2)(2(2 2 2 −+     −++ aaaa a )2(2)2( ++− aaa 42 +a 320)80( =−+ xx 80)320( =−− xx 200=x 12080 =−x    =− =+ 80 320 yx yx    = = 120 200 y x    ≥−+ ≥−+ 120)8(2010 200)8(2040 xx xx 42 ≤≤ x ②甲车 3 辆，乙车 5 辆； ③甲车 4 辆，乙车 4 辆． …………………………6 分 （3）3 种方案的运费分别为： ①2×4000+6×3600＝29600； ②3×4000+5×3600＝30000； ③4×4000+4×3600＝30400． …………………………8 分 ∴方案①运费最少，最少运费是 29600 元． …………………………9 分 （注：用一次函数的性质说明方案①最少也不扣分．） 22．（1）方法一：由已知得：C（0，－3），A（－1，0） …………………………1 分 将 A、B、C 三点的坐标代入得 …………………………2 分 解得： …………………………3 分 所以这个二次函数的表达式为： …………………………3 分 方法二：由已知得：C（0，－3），A（－1，0） …………………………1 分 设该表达式为： …………………………2 分 将 C 点的坐标代入得： …………………………3 分 所以这个二次函数的表达式为： …………………………3 分 （注：表达式的最终结果用三种形式中的任一种都不扣分） （2）方法一：存在，F 点的坐标为（2，－3） …………………………4 分 理由：易得 D（1，－4），所以直线 CD 的解析式为： ∴E 点的坐标为（－3，0） …………………………4 分 由 A、C、E、F 四点的坐标得：AE＝CF＝2，AE∥CF ∴以 A、C、E、F 为顶点的四边形为平行四边形 ∴存在点 F，坐标为（2，－3） …………………………5 分 方法二：易得 D（1，－4），所以直线 CD 的解析式为： ∴E 点的坐标为（－3，0） …………………………4 分 ∵以 A、C、E、F 为顶点的四边形为平行四边形 ∴F 点的坐标为（2，－3）或（―2，―3）或（－4，3） 代入抛物线的表达式检验，只有（2，－3）符合 ∴存在点 F，坐标为（2，－3） …………………………5 分 （3）如图，①当直线 MN 在 x 轴上方时，设圆的半径为 R（R>0），则 N（R+1，R）， 代入抛物线的表达式，解得 …………6 分 ②当直线 MN 在 x 轴下方时，设圆的半径为 r（r>0）， 则 N（r+1，－r），    −= =++ =+− 3 039 0 c cba cba    −= −= = 3 2 1 c b a 322 −−= xxy )3)(1( −+= xxay 1=a 322 −−= xxy 3−−= xy 3−−= xy 2 171+=R 代入抛物线的表达式，解得 ………7 分 ∴圆的半径为 或 ． ……………7 分 （4）过点 P 作 y 轴的平行线与 AG 交于点 Q， 易得 G（2，－3），直线 AG 为 ．……………8 分 设 P（x， ），则 Q（x，－x－1），PQ ． …………………………9 分 当 时，△APG 的面积最大 此时 P 点的坐标为 ， ． …………………………10 分 2009 年深圳市初中毕业生学业考试数学试卷 说明： 1.全卷分二部分，第一部分为选择题，第二部分为非选择题，共 4 页。考试时间 90 分钟，满分 100 分。 第一部分 选择题 一、选择题（本题有 10 小题，每题 3 分，共 30 分） 1．如果 a 的倒数是 1，那么 a2009 等于（ ） A．1 B． 1 C．2009 D． 2009 2．由若干个相同的小立方体搭成的几何体的三视图如图所示，则搭成这个几何体的小立方体的个数是（ ） A．3 B．4 C．5 D．6 2 171+−=r 2 171+ 2 171+− 1−−= xy 322 −− xx 22 ++−= xx 3)2(2 1 2 ×++−=+= ∆∆∆ xxSSS GPQAPQAPG 2 1=x      − 4 15,2 1 8 27的最大值为APGS∆ − − − A O BC x y 主视图 左视图 俯视图 3．用配方法将代数式 a2+4a-5 变形，结果正确的是（ ） A.(a+2)2-1 B. (a+2)2-5 C. (a+2)2+4 D. (a+2)2-9 4．横跨深圳及香港之间的深圳湾大桥（Shenzhen Bay Bridge）是中国唯一倾斜的独塔单索面桥，大桥全长 4770 米， 这个数字用科学计数法表示为（保留两个有效数字）（ ） A． B． C． D． 5．下面的图形中，既是轴对称图形又是中心对称图形的是（ ） A． B． C． D． 6．下图是同一副扑克中的 4 张扑克牌的正面，将它们正面朝下洗匀后放在桌上，小明从中抽出一张，则抽到偶数的概 率是（ ） A． B． C． D． 7．如图，反比例函数 的图象与直线 的交点 为 A，B，过点 A 作 y 轴的平行线与过点 B 作 x 轴的平 行线相交于点 C，则 的面积为（　　） A．8 B．6 C．4 D．2 8．如图，数轴上与 1， 对应的点分别为 A，B，点 B 关于点 A 的对称点为 C，设点 C 表示的数为 x，则 （　　） A． B． C． D．2 9．某商场的老板销售一种商品，他要以不低于进价 20%价格才能出售，但为了获得更多利润，他以高出进价 80%的价 格标价．若你想买下标价为 360 元的这种商品，最多降价多少时商店老板才能出售（　　） A．80 元 B．100 元 C．120 元 D．160 元 10．如图，已知点A、B、C、D均在已知圆上，AD//BC，AC平分 ， ，四边形ABCD的周长为 10cm．图中阴影部分的面积为（ ） A. B. C. D. 第二部分（非选择题，共 70 分） 二、填空题（本题有 6 小题，每题 3 分，共 18 分） 11．小明在 7 次百米跑练习中成绩如下： 1 3 1 2 3 4 2 3 次数 第一次 第二次 第三次 第四次 第五次 第六次 第七次 成绩/秒 12.8 12.9 13.0 12.7 13.2 13.1 12.8 247 10× 34.7 10× 34.8 10× 35.0 10× 4y x = − 1 3y x= − ABC△ 2 22x x − + = 2 2 2 3 2 BCD∠ 120ADC = ∠ 3 2 3 2 3 4 3 A D CB O C A B x 21 则这 7 次成绩的中位数是 秒 12．小明和小兵两人参加学校组织的理化实验操作测试， 近 期 的 5 次测试成绩如图所示，则小明 5 次成绩的方差 与 小 兵 5 次 成 绩 的 方 差 之 间 的 大 小 关 系 为 　　　　 ． （ 填“>”、“<”、“＝”） 13．如图，矩形 ABCD 中，由 8 个面积均为 1 的小正方形组成的 L 型模板如图放置，则矩形 ABCD 的周长为 _． 14．已知 依据上述规律，则 ． 15．如图 a 是长方形纸带，∠DEF=20°，将纸带沿 EF 折叠成图 b，再沿 BF 折叠成图 c，则图 c 中的∠CFE 的度数是 ． 16．刘谦的魔术表演风靡全国，小明也学起了刘谦发明了一个魔术盒，当任意实数对（a，b）进入其中时，会得到一 个新的实数：a2+b-1，例如把（3，-2）放入其中，就会得到 32+（-2）-1=6.现将实数对（m，-2m）放入其中，得到实数 2，则 m= ． 三、解答题（本大题有 7 题，共 52 分） 17．（6 分）计算： ． 18．（6 分）先阅读理解下面的例题，再按要求解答： 例题：解一元二次不等式 . 解：∵ ， ∴ . 由有理数的乘法法则“两数相乘，同号得正”，有 （1） （2） 解不等式组（1），得 ， 解不等式组（2），得 ， 故 的解集为 或 ， 即一元二次不等式 的解集为 或 . 问题：求分式不等式 的解集. 2 1S 2 2S 2 1S 2 2S 1 2 3 1 1 2 1 1 3 1 1 4, , ,...,1 2 3 2 3 2 3 4 3 8 3 4 5 4 15a a a= + = = + = = + =× × × × × × 99a = 2 2 02 ( 3) ( 3.14) 8sin 45π−− − − + − − ° 2 9 0x − > 2 9 ( 3)( 3)x x x− = + − ( 3)( 3) 0x x+ − > 3 0 3 0 x x + >  − > 3 0 3 0 x x + <  − < 3x > 3x < − ( 3)( 3) 0x x+ − > 3x > 3x < − 2 9 0x − > 3x > 3x < − 5 1 02 3 x x + <− A D A CB A E A C A B A F A D A C D B A E A F C A G B A A B A E A F C A G B A A 图 a 图 b 图 c 12 10 8 6 4 2 0 1 2 3 4 5 小明 小兵 19．（6 分）如图，斜坡 AC 的坡度（坡比）为 1: ，AC＝10 米．坡顶有一旗杆 BC，旗杆顶端 B 点与 A 点有一条彩 带 AB 相连，AB＝14 米． 试求旗杆 BC 的高度． 20．（7 分）深圳大学青年志愿者协会对报名参加 2011 年深圳大运会志愿者选拔活动的学生进行了一次与大运知识有 关的测试，小亮对自己班有报名参加测试的同学的测试成绩作了适当的处理，将成绩分成三个等级:一般、良好、优 秀，并将统计结果绘成了如下两幅不完整的统计图，请你根据图中所给信息解答下列问题： （1）请将两幅统计图补充完整； （2）小亮班共有 名学生参加了这次测试，如果青年志愿者协会决定让成绩为“优秀”的学生参加下一轮的测试, 那么小亮班有 人将参加下轮测试； （3）若这所高校共有 1200 名学生报名参加了这次志愿者选拔活动的测试，请以小亮班的测试成绩的统计结果来估算 全校共有多少名学生可以参加下一轮的测试。 21．（8 分）迎接大运，美化深圳，园林部门决定利用现有的 3490 盆甲种花卉和 2950 盆乙种花卉搭配 A、B 两种园艺 造型共 50 个摆放在迎宾大道两侧，已知搭配一个 A 种造型需甲种花卉 80 盆，乙种花卉 40 盆，搭配一个 B 种造型 需甲种花卉 50 盆，乙种花卉 90 盆． （1）某校九年级（1）班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请 你帮助设计出来． （2）若搭配一个 A 种造型的成本是 800 元，搭配一个 B 种造型的成本是 960 元，试说明（1）中哪种方案成本最 低？最低成本是多少元？ 22．（9 分）如图，在直角坐标系中，点 A 的坐标为（－2，0），连结 OA，将线段 OA 绕原点 O 顺时针旋转 120°，得 到线段 OB. （1）求点 B 的坐标； 3 A B C D （2）求经过 A、O、B 三点的抛物线的解析式； （3）在（2）中抛物线的对称轴上是否存在点 C，使△BOC 的周长最小？若存在，求出点 C 的坐标；若不存在， 请说明理由. （4）如果点 P 是（2）中的抛物线上的动点，且在 x 轴的下方，那么△PAB 是否有最大面积？若有，求出此时 P 点的坐标及△PAB 的最大面积；若没有，请说明理由。 23．如图，在平面直角坐标系中，直线 l：y=－2x－8 分别与 x 轴，y 轴相交于 A，B 两点，点 P（0，k）是 y 轴的负半 轴上的一个动点，以 P 为圆心，3 为半径作⊙P. （1）连结 PA，若 PA=PB，试判断⊙P 与 x 轴的位置关系，并说明理由； （2）当 k 为何值时，以⊙P 与直线 l 的两个交点和圆心 P 为顶点的三角形是正三角形？ B A O y x 2009 年深圳市初中毕业生学业考试数学试卷参考答案 一、选择题 1. B；2. B ；3. D；4. C；5. C；6. C ；7. A；8. C；9. C ；10. B ； 二、填空题 11. 12.9；12. ＜；13. ；14. ；15. 120° ；16. 3 或－1； 三、解答题 17. ． 18. 解：由有理数的除法法则“两数相除，同号得正”，有 （1） （2） 解不等式组（1），得 ，解不等式组（2），得无解， 故分式不等式 的解集为 . 19. 解：延长 BC 交 AD 于 E 点，则 CE⊥AD． 在 Rt△AEC 中，AC＝10， 由坡比为 1︰ 可知：∠CAE＝30°， ∴ CE＝AC·sin30°＝10× ＝5， AE＝AC·cos30°＝10× ＝ ． 在 Rt△ABE 中，BE＝ ＝ ＝11． ∵ BE＝BC＋CE，∴ BC＝BE－CE＝11-5＝6（米）． 答：旗杆的高度为 6 米． 20. 解：（1）略；（2）40，20；（3）600． 21. 解：设搭配 A 种造型 x 个，则 B 种造型为 个， 依题意，得： 解得： ，∴ ∵x 是整数，x 可取 31、32、33， ∴可设计三种搭配方案：①A 种园艺造型 31 个，B 种园艺造型 19 个；②A 种园艺造型 32 个，B 种园艺造型 18 个；③ A 种园艺造型 33 个，B 种园艺造型 17 个． （2）方法一：由于 B 种造型的造价成本高于 A 种造型成本．所以 B 种造型越少，成本越低，故应选择方案③， 成本最低，最低成本为：33×800+17×960=42720（元） 方法二：方案①需成本：31×800+19×960=43040（元）； 8 5 100 9999 17 4 − 5 1 0 2 3 0 x x + >  − < 5 1 0 2 3 0 x x + <  − > 1 35 x− < < 5 1 02 3 x x + <− 1 35 x− < < 3 1 2 3 2 5 3 2 2AB AE− 2 214 (5 3)− (50 )x− 80 50(50 ) 3490 40 90(50 ) 2950 x x x x + −  + − ≤ ≤ 33 31 x x    ≤ ≥ 31 33x≤ ≤ A B C D E 方案②需成本：32×800+18×960=42880（元）； 方案③需成本：33×800+17×960=42720（元）； ∴应选择方案③，成本最低，最低成本为 42720 元． 22. 解：（1）B（1， ） （2）设抛物线的解析式为 y=ax(x+a)，代入点 B（1, ），得 ， 因此 （3）如图，抛物线的对称轴是直线 x=—1，当点 C 位于对称轴与线段 AB 的交点时，△BOC 的周长最小. 设直线 AB 为 y=kx+b.所以 ， 因此直线 AB 为 ， 当 x=－1 时， ， 因此点 C 的坐标为（－1， ）. （4）如图，过 P 作 y 轴的平行线交 AB 于 D. 当 x=－ 时，△PAB 的面积的最大值为 ，此时 . 23. 解：（1）⊙P 与 x 轴相切. ∵直线 y=－2x－8 与 x 轴交于 A（4，0）， 与 y 轴交于 B（0，－8）， ∴OA=4，OB=8. 由题意，OP=－k， ∴PB=PA=8+k. 在 Rt△AOP 中，k2+42=(8+k)2， ∴k=－3，∴OP 等于⊙P 的半径， ∴⊙P 与 x 轴相切. （2）设⊙P 与直线 l 交于 C，D 两点，连结 PC，PD 当圆心 P 在线段 OB 上时,作 PE⊥CD 于 E. ∵△PCD 为正三角形，∴DE= CD= ，PD=3， ∴PE= . ∵∠AOB=∠PEB=90°， ∠ABO=∠PBE， 3 3 3 3a = 23 2 3 3 3y x x= + 3 3, 3 2 0. 2 3 3 kk b k b b  = + =  − + =  = 解得 3 2 3 3 3y x= + 3 3y = 3 2 2 2 1 ( )( )2 1 3 2 3 3 2 3 32 3 3 3 3 3 3 32 2 3 1 9 3 2 2 8 PAB PAD PBD D P B AS S S y y x x x x x x x x ∆ ∆ ∆= + = − −     = + − + ×             = − − +  = − + +   1 2 9 3 8 1 3,2 4P  − −    1 2 3 2 3 3 2 C B A O y x D B A O y x P ∴△AOB∽△PEB， ∴ ， ∴ ∴ ， ∴ ， ∴ . 当圆心 P 在线段 OB 延长线上时,同理可得 P(0,－ －8)， ∴k=－ －8， ∴当 k= －8 或 k=－ －8 时，以⊙P 与直线 l 的两个交点和圆心 P 为顶点的三角形是正三角形. 3 3 4 2, = 4 5 AO PE AB PB PB = 即 3 15 ,2PB = 3 158 2PO BO PB= − = − 3 15(0, 8)2P − 3 15 82k = − 3 15 2 3 15 2 3 15 2 3 15 2 深圳市 2010 年初中毕业生学业考试 数 学 试 卷 第一部分 选择题 （本部分共 12 小题，每小题 3 分，共 36 分．每小题给出的 4 个选项中，其中只有一个是正确的） 1．－2 的绝对值等于 A．2 B．－2 C． 1 2 D．4 2．为保护水资源，某社区新建了雨水再生工程，再生水利用量达 58600 立方米/年。这个数据用科学记数法表示为（保 留两个有效数字） A．58×103 B．5.8×104 C．5.9×104 D．6.0×104 3．下列运算正确的是 A．(x－y)2＝x2－y2 B．x2·y2 ＝(xy)4 C．x2y＋xy2 ＝x3y3 D．x6÷y2 ＝x4 4．升旗时，旗子的高度 h(米)与时间 t(分)的函数图像大致为 5．下列说法正确的是 A．“打开电视机，正在播世界杯足球赛”是必然事件 B．“掷一枚硬币正面朝上的概率是 1 2”表示每抛掷硬币 2 次就有 1 次正面朝上 C．一组数据 2，3，4，5，5，6 的众数和中位数都是 5 D．甲组数据的方差 S 甲 2＝0.24，乙组数据的方差 S 甲 2＝0.03，则乙组数据比甲组数据稳定 6.下列图形中，是中心对称图形但不是轴对称图形的是 7．已知点 P（a－1，a＋2）在平面直角坐标系的第二象限内，则 a 的取值范围在数轴上可表示为（阴影部分） 8．观察下列算式，用你所发现的规律得出 22010 的末位数字是 A B C D 1－2－3 －1 0 2A． 1－2－3 －1 0 2B． C． 1－2－3 －1 0 2 D． 1－2－3 －1 0 2 t h O t h O t h O t h O A B C D A B C D 图 3 E A B CD 图 1 xO y P 图 2 21＝2，22＝4，23＝8，24＝16，25＝32，26＝64，27＝128，28＝256，…， A．2 B．4 C．6 D．8 9．如图 1，△ABC 中，AC＝AD＝BD，∠DAC＝80º，则∠B 的度数是 A．40º B．35º C．25º D．20º 10．有四张质地相同的卡片，它们的背面相同，其中两张的正面印有“粽子”的图案，另外两张的正面印有“龙舟” 的图案，现将它们背面朝上，洗均匀后排列在桌面，任意翻开两张，那么两张图案一样的概率是 A． 1 3 B． 1 2 C．2 3 D． 3 4 11．某单位向一所希望小学赠送 1080 件文具，现用 A、B 两种不同的包装箱进行包装，已知每个 B 型包装箱比 A 型包 装箱多装 15 件文具，单独使用 B 型包装箱比单独使用 A 型包装箱可少用 12 个。设 B 型包装箱每个可以装 x 件文 具，根据题意列方程为 A． 1080 x ＝ 1080 x－15＋12 B． 1080 x ＝ 1080 x－15－12 C． 1080 x ＝ 1080 x＋15－12 D． 1080 x ＝ 1080 x＋15＋12 12．如图 2，点 P（3a，a）是反比例函 y＝ k x（k＞0）与⊙O 的一个交点， 图中阴影部分的面积为 10π，则反比例函数的解析式为 A．y＝ 3 x B．y＝ 5 x C．y＝ 10 x D．y＝ 12 x 第二部分 非选择题 填空题（本题共 4 小题，每小题 3 分，共 12 分．） 13．分解因式：4x2－4＝_______________． 14．如图 3，在□ABCD 中，AB＝5，AD＝8，DE 平分∠ADC，则 BE＝_______________． 15．如图 4，是一个由若干个相同的小正方体组成的几何体的主视图和俯视图，则能组成这个几何体的小正方体的个数 最少是____________个． 16．如图 5，某渔船在海面上朝正东方向匀速航行，在 A 处观测到灯塔 M 在北偏东 60º方向上，航行半小时后到达 B 处，此时观测到灯塔 M 在北偏东 30º方向上，那么该船继续航行____________分钟可使渔船到达离灯塔距离最近 的位置． 填空题（本题共 7 小题，其中第 17 小题 6 分，第 18 小题 6 分，第 19 小题 7 分，第 20 小题 7 分，第 21 小题 8 分，第 22 小题 9 分，第 23 小题 9 分，共 52 分．） 17．（本题 6 分）计算：( 1 3)－2－2sin45º＋ (π －3.14)0＋ 1 2 8＋(－1)3． 18．（本题 6 分）先化简分式 a2－9 a2＋6a＋9÷ a－3 a2＋3a－ a－a2 a2－1，然后在 0，1，2，3 中选一个你认为合适的 a 值，代入求 值． 19．（本题 7 分）低碳发展是今年深圳市政府工作报告提出的发展理念．近期，某区与某技术支持单位合作，组织策划 A B M 图 5 北 M 北 M 30º M 60º M 东 图 4 主视图 俯视图 了该区“低碳先锋行动”，开展低碳测量和排行活动．根据调查数据制作了频数分布直方图和扇形统计图，图 6 中 从左到右各长方形的高度之比为 2:8:9:7:3:1． （1）已知碳排放值 5≤x＜7（千克/平方米·月）的单位有 16 个，则此次行动调查了________个单位；（3 分） （2）在图 7 中，碳排放值 5≤x＜7（千克/平方米·月）部分的圆心角为________度；（2 分） （3）小明把图 6 中碳排放值 1≤x＜2 的都看成 1.5，碳排放值 2≤x＜3 的都看成 2.5，以此类推，若每个被检单位 的建筑面积均为 10000 平方米，则按小明的办法，可估算碳排放值 x≥4（千克/平方米·月）的被检单位一个 月的碳排放总值约为________________吨．（2 分） 20．（本题 7 分）如图 8，△AOB 和△COD 均为等腰直角三角形，∠AOB＝∠COD＝90º，D 在 AB 上． （1）求证：△AOB≌△COD；（4 分） （2）若 AD＝1，BD＝2，求 CD 的长．（3 分） 21．（本题 8 分）儿童商场购进一批 M 型服装，销售时标价为 75 元/件，按 8 折销售仍可获利 50%．商场现决定对 M 型服装开展促销活动，每件在 8 折的基础上再降价 x 元销售，已知每天销售数量 y（件）与降价 x 元之间的函数关 系为 y＝20＋4x（x＞0） （1）求 M 型服装的进价；（3 分） （2）求促销期间每天销售 M 型服装所获得的利润 W 的最大值．（5 分） 销售，已知每天销售数量与降价 22．（本题 9 分）如图 9，抛物线 y＝ax2＋c（a＞0）经过梯形 ABCD 的四个顶点，梯形的底 AD 在 x 轴上，其中 A（－ 2,0），B（－1, －3）． （1）求抛物线的解析式；（3 分） （2）点 M 为 y 轴上任意一点，当点 M 到 A、B 两点的距离之和为最小时，求此时点 M 的坐标；（2 分） （3）在第（2）问的结论下，抛物线上的点 P 使 S△PAD＝4S△ABM 成立，求点 P 的坐标．（4 分） A B C D 图 8 O 0 1 2 3 4 5 6 7 单位碳排放值 x (千克/平方米.月) 单位数 图 6 图 7 5≤x＜7 1≤x＜3 3≤x＜5 23．（本题 9 分）如图 10，以点 M（－1,0）为圆心的圆与 y 轴、x 轴分别交于点 A、B、C、D，直线 y＝－ 3 3 x－ 5 3 3 与⊙M 相切于点 H，交 x 轴于点 E，交 y 轴于点 F． （1）请直接写出 OE、⊙M 的半径 r、CH 的长；（3 分） （2）如图 11，弦 HQ 交 x 轴于点 P，且 DP:PH＝3:2，求 cos∠QHC 的值；（3 分） （3）如图 12，点 K 为线段 EC 上一动点（不与 E、C 重合），连接 BK 交⊙M 于点 T，弦 AT 交 x 轴于点 N．是否存 在一个常数 a，始终满足 MN·MK＝a，如果存在，请求出 a 的值；如果不存在，请说明理由．（3 分） 参 考 答 案 第一部分：选择题 1、A 2、C 3、 D 4、B 5、D 6、A 7、C 8、B 9、C 10、A 11、B 12、D 第二部分：填空题：13、 14、3 15、9 16、154( 1)( 1)x x+ − xD A B H CE M O F 图 10 x y D A B H CE M O 图 11 P Q x y D A B H CE M O F 图 12 N K y x y CB _D_A O 图 9 解答题： 17、原式= 18、 当 时，原式=4 19、（1）、120；（2）、 ；（3） 20、（1）证明：如右图 1， ， 又 ， （2）由 有： ， ， ，故 21、（1）、设进价为 元，依题意有： ，解之得： （元） （2）、依题意， 故当 （元）时， （元） 22、（1）、因为点 A、B 均在抛物线上，故点 A、B 的坐标适合抛物线方程 ∴ 解之得： ；故 为所求 （2）如图 2，连接 BD，交 y 轴于点 M，则点 M 就是所求作的点 设 BD 的解析式为 ，则有 ， ， 故 BD 的解析式为 ；令 则 ，故 (3)、如图 3，连接 AM，BC 交 y 轴于点 N，由（2）知，OM=OA=OD=2， 易知 BN=MN=1，易求 ；设 ， 依题意有： ，即： 解之得： ， ，故 符合条件的 P 点有三个： 23、（1）、如图 4，OE=5， ，CH=2 （2）、如图 5，连接 QC、QD，则 ， 19 2 2 1 2 2 1 92 − + + × − = 2 2 ( 3)( 3) ( 3) 2( 3) 3 1 a a a a a a a a aa a a + − + −= − = + =+ − −原式 2a = 48° 32.18 10× 1 90 3, 2 90 3° °∠ = − ∠ ∠ = − ∠ 1 2∴∠ = ∠ ,OC OD OA OE= = AOC BOD∴∆ ≅ ∆ AOC BOD∆ ≅ ∆ 2AC BD= = 45CAO DBO °∠ = ∠ = 90CAB∴∠ = ° 2 2 2 22 1 5CD AC AD= + = + = a (1 50 ) 75 80a + % = × % 40a = 2 15(20 4 )(60 40 ) 4 60 400 4( ) 6252W x x x x x= + − − = − + + = − − + 15 7.52x = = 625W =最大 4 0 3 a c a c + =  + = − 1 4 a c =  = − 2 4y x= − y kx b= + 2 0 3 k b k b + = − + = − 1 2 k b =  = − 2y x= − 0,x = 2y = − (0, 2)M − 90AMB∠ = ° 2 2, 2AM BM= = 1 2 2 2 22ABMS = × × =  2( , 4)P x x − 21 4 4 22 AD x − = × 21 4 4 4 22 x× − = × 2 2x = ± 0x = 1 2 3(2 2,4), ( 2 2,4), (0, 4)P P P− − 2r = 90CQD∠ = ° QHC QDC∠ = ∠ x y M CB DA O 图 2 x y D A B H C E M O F 图 4 x y N M O P2 P1 B DA P3 C 图 3 图 1 32 1 C A O B D 易知 ，故 ， ， ，由于 ， ； （3）、如图 6，连接 AK，AM，延长 AM， 与圆交于点 G，连接 TG，则 ， 由于 ，故， ； 而 ，故 在 和 中， ； 故 ； ; 即： 故存在常数 ，始终满足 常数 深圳市 2011 年初中毕业生学业考试 数学试卷 第一部分 选择题 （本部分共 12 小题，每小题 3 分，共 36 分。每小题给出的 4 个选项中，其中只有一个是正确的） 1． 的相反数等于（ ） A． B． C．－2 D．2 2．如图 1 所示的物体是一个几何体，其主视图是（ ） CHP DQP∆ ∆ DP DQ PH CH = 3 2 2 DQ= 3DQ = 4CD = 3cos cos 4 QDQHC QDC CD ∴ ∠ = ∠ = = 90GTA∠ = ° 2 4 90∴∠ + ∠ = ° 3 4∠ = ∠ 2 3 90°∴∠ + ∠ = 3 90BKO∠ + ∠ = ° 2BKO∠ = ∠ 1BKO∠ = ∠ 1 2∠ = ∠ AMK∆ NMA∆ 1 2∠ = ∠ AMK NMA∠ = ∠ AMK NMA∆  MN AM AM MK = 2 4MN MK AM= = a MN MK a= 4a = 1 2 − 1 2 − 1 2 图 5 x y P D A B H C E M O Q F 4 3 2 1 x y NT D A B H CE M O K G F 图 6 1 A B C 图 3 1 2 3 6 7 8 A． B． C． D． 图 1 3．今年参加我市初中毕业生学业考试的总人数约为 56000 人，这个数据用科学记数法表示为（ ） A．5.6×103 B．5.6×104 C．5.6×105 D．0.56×105 4．下列运算正确的是（ ） A．x2＋x3＝x5 B．(x＋y)2＝x2＋y2 C．x2·x3＝x6 D．(x2)3＝x6 5．某校开展为“希望小学”捐书活动，以下是八名学生捐书的册数：2，3，2，2，6，7，6，5，则这组数据的 中位数为（ ） A．4 B．4.5 C．3 D．2 6 ． 一 件 服 装 标 价 200 元 ， 若 以 6 折 销 售 ， 仍 可 获 利 20% ， 则 这 件 服 装 的 进 价 是 （ ） A ． 100 元 B．105 元 C．108 元 D．118 元 7．如图 2，小正方形的边长均为 1，则下列图形中的三角形（阴影部分）与△ABC 相似的是（ ） 图 2 A． B． C． D． 8．如图 3 是两个可以自由转动的转盘，转盘各被等分成三个扇形， 并分别标上 1，2，3 和 6，7，8 这 6 个数字。如果同时转动 两个转盘各一次（指针落在等分线上重转），当转盘停止后， 则指针指向的数字和为偶数的概率是（ ） A． B． C． D． 9．已知 a，b，c 均为实数，若 a>b，c≠0。下列结论不一定正确的是（ ） A． B． C． D． 10．对抛物线 而言，下列结论正确的是（ ） A．与 x 轴有两个交点 B．开口向上 C．与 y 轴的交点坐标是（0，3） D．顶点坐标为（1，－2） 11．下列命题是真命题的个数有（ ） ①垂直于半径的直线是圆的切线； ②平分弦的直径垂直于弦； ③若 是方程 x－ay＝3 的一个解，则 a＝－1； ④若反比例函数 的图像上有两点（ ，y1），（1，y2），则 y1 + c a c b− > − 2 2 a b c c > 2 2a ab b> > 2 2 3y x x= − + − 1 2 x y =  = 3y x = − 1 2 3 :1 2 :1 A B C D F E O 图 4 A B C 图 7 x y O O A B 图 5 [来源:学.科.网] 第二部分 非选择题 填空题（本题共 4 小题，每小题 3 分，共 12 分。） 13．分解因式：a3－a＝______________________。 14．如图 5，在⊙O 中，圆心角∠AOB＝120°，弦 AB＝ cm， 则 OA＝___________cm。 15．如图 6，这是由边长为 1 的等边三角形摆出的一系列图形，按这种方式摆下去，则第 n 个图形的 周长是＝______________________。 （1） （2） （3） （4） …… 图 6 16．如图 7，△ABC 的内心在 y 轴上，点 C 的坐标为（2，0），点 B 的 坐标为（0，2），直线 AC 的解析式为： ，则 tanA 的值 是___________。 解答题（本题共 7 小题，其中第 17 小题 5 分，第 18 小题 6 分，第 19 小题 7 分，第 20 小题 8 分，第 21 小题 8 分，第 22 小题 9 分，第 23 小题 9 分，共 52 分） 17．（本题 5 分）计算： 。 18．（本题 6 分）解分式方程： 。 19．（本题 7 分）某校为了了解本校八年级学生课外阅读的喜欢， 随机抽取了该校八年级部分学生进行问卷调查 （每人只选一种书籍）。图 8 是整理数据后绘制的两幅不完整的统计图，请你根据图中提供的信息，解答下列问 题： 2 3 1 12y x= − 1 0 02 3 30 5 ( 2011)cos π− + + − − − 2 3 21 1 x x x + =+ − …… 人数 100 80 60 40 漫画 科普 常识 其他 种类小说 0 20 80 40 20 25% 小 说 30% 科普常识 漫画 其他 图 11 A B D C C′ G G 图 12 A B D C EC′ N M O A E CB D 图 10 O A E CB D 图 9 图 8 （1）这次活动一共调查了_________名学生； （2）在扇形统计图中，“其他”所在扇形圆心角等于_________度； （3）补全条形统计图； （4）若该年级有 600 人，请你估计该年级喜欢“科普常识”的学生人数约是_________人。 20．如图 9，已知在⊙O 中，点 C 为劣弧 AB 上的中点，连接 AC 并延长至 D，使 CD＝CA，连接 DB 并延长交⊙O 于点 E，连接 AE。 （1）求证：AE 是⊙O 的直径； （2）如图 10，连接 EC，⊙O 半径为 5，AC 的长为 4， 求阴影部分的面积之和。（结果保留π与根号） 21．（本题 8 分）如图 11，一张矩形纸片 ABCD，其中 AD＝8cm，AB＝6cm，先沿对角线 BD 对折，[点 C 落在点 C′ 的位置，BC′ 交 AD 于点 G。 （1）求证：AG＝C′ G； （2）如图 12，再折叠一次，使点 D 与点 A 重合， 得折痕 EN，EN 交 AD 于点 M，求 EM 的长。 22．（本题 9 分）深圳某科技公司在甲地、乙地分别生产了 17 台、15 台同一种型号的检测设备，全部运往大运赛 场 A、B 馆，其中运往 A 馆 18 台、运往 B 馆 14 台；运往 A、B 两馆的运费如 表 1： 出 发 地目 的 地 甲 地 乙 地 A 馆 800 元∕台 700 元∕台 B 馆 500 元∕台 600 元∕台 表 1 出 发 地目 的 地 甲 地 乙 地 A 馆 x（台） _______（台） B 馆 _______（台）_______（台） 表 2 （1）设甲地运往 A 馆的设备有 x 台，请填写表 2，并求出总费用 y（元） 与 x（台）的函数关系式； （2）要使总费用不高于 20200 元，请你帮忙该公司设计调配方案，并写出有哪几种方案； （3）当 x 为多少时，总运费最小，最小值是多少？ [来源:学#科#网 Z#X#X#K] 23．（本题 9 分）如图 13，抛物线 y＝ax2＋bx＋c（a≠0）的顶点为 C（1，4），交 x 轴于 A、B 两点，交 y 轴于点 D，其中点 B 的坐标为（3，0）。 （1）求抛物线的解析式； （2）如图 14，过点 A 的直线与抛物线交于点 E，交 y 轴于点 F，其中点 E 的横坐标为 2，若直线 PQ 为抛物线 的对称轴，点 G 为直线 PQ 上的一动点，则 x 轴上师范存在一点 H，使 D、G、H、F 四点所围成的四边形周长最小。 若存在，求出这个最小 值及点 G、H 的坐标；若不存在，请说明理由。 （3）如图 15，在抛物线上是否存在一点 T，过点 T 作 x 轴的垂线，垂足为点 M，过点 M 作 MN∥BD，交线段 AD 于点 N，连接 MD，使△DNM∽△BMD。若存在，求出点 T 的坐标；若不存在，请说明理由。 深圳市 2011 年初中毕业生学业考试 图 13 A B x y O D C 图 14 A B x y O D C P Q E F 图 15 A B x y O D C 人数 100 80 60 40 漫画 科普 常识 其他 种类小说 0 20 80 40 60 20 图 1 O A E CB D 图 3 O A E CB D 图 2 数学试卷·参考答案 第一部分：选择题 题 号 1 2 3 4 5 6[] 7 8 9 10 11 12 答 案 B C B D A A B C D D C A 第二部分：填空题： 13、a(a＋1)(a－1) 14、4 15、2＋n 16、 解答题： 17、原式 18、解：方程两边同时乘以：(x＋1)(x－1)，得： 2x (x－1)＋3(x＋1)＝2(x＋1)(x－1) 整理化简，得 x＝－5 经检验，x＝－5 是原方程的根 原方程的解为： x＝－5 （备注：本题必须验根，没有验根的扣 2 分） 19、（1）200； （2）36； （3）如图 1； （4）180 20、（1）证明：如图 2，连接 AB、BC， ∵点 C 是劣弧 AB 上的中点 ∴ ∴CA＝CB 又∵CD＝CA ∴CB＝CD＝CA ∴在△ABD 中， ∴∠ABD＝90° ∴∠ABE＝90° ∴AE 是⊙O 的直径 （2）解：如图 3，由（1）可知，AE 是⊙O 的直径 ∴∠ACE＝90° ∵⊙O 的半径为 5，AC＝4 ∴AE＝10，⊙O 的面积为 25π 在 Rt△ACE 中，∠ACE＝90°，由勾股定理，得： 1 3 1 3 5 1 62 2 = + + − =  CA CB= 1 2CB AD= ∴S△ACE＝ ∴S 阴影＝ S⊙O－S△ACE＝ 21、（1）证明：如图 4，由对折和图形的对称性可知， CD＝C′ D，∠C＝∠C′ ＝90° 在矩形 ABCD 中，AB＝CD，∠A＝∠C＝90° ∴AB＝ C′ D，∠A＝∠C′ 在△ABG 和△C′ DG 中， ∵AB＝ C′ D，∠A＝∠C′ ， ∠AGB＝∠C′ G D ∴△ABG≌△C′ DG（AAS） ∴AG＝C′ G （2）解：如图 5，设 EM＝x，AG＝y，则有： C′ G＝y，DG＝8－y， ， 在 Rt△C′ DG 中，∠DC′ G＝90°，C′ D＝CD＝6， ∴ C′ G2＋C′ D2＝DG2 即：y2＋62＝（8－y）2 解得： ∴C′ G＝ cm，DG＝ cm 又∵△DME∽△DC′ G ∴ ， 即： 解得： ， 即：EM＝ （cm） ∴所求的 EM 长为 cm。 22、解：（1）表 2 如右图所示，依题意，得： y＝800x＋700(18－x)＋500(17－x)＋600(x－3) 即：y＝200x＋19300（3≤x≤17） （2）∵要使总运费不高于 20200 元 ∴200x＋19300<20200 2 2 2 210 4 2 21CE AE AC= − = − = 1 1 4 2 21 4 212 2AC CE× × = × × = 1 2 1 2525 4 21 4 212 2 ππ× − = − 1 42DM AD cm= = 7 4y = 7 4 25 4 DM ME DC C G =′ ′ 4 76 ( )4 x= 7 6x = 7 6 7 6 图 4 A B D C C′ G G 图 5 A B D C EC′ N M 解得： ∵3≤x≤17，且设备台数 x 只能取正整数 ∴ x 只能取 3 或 4。 ∴该公司的调配方案共有 2 种，具体如下表： 表 3 表 4 （3）由（1）和（2）可知，总运费 y 为： y＝200x＋19300（x＝3 或 x＝4） 由一次函数的性质，可知： 当 x＝3 时，总运费最小，最小值为：ym i n＝200×3＋19300＝19900（元）。 答：当 x 为 3 时，总运费最小，最小值是 19900 元。 23、解：（1）设所求抛物线的解析式为：y＝a(x－1)2＋4， 依题意，将点 B（3，0）代入，得： a(3－1)2＋4＝0 解得：a＝－1 ∴所求抛物线的解析式为：y＝－(x－1)2＋4 （2）如图 6，在 y 轴的负半轴上取一点 I，使得点 F 与点 I 关于 x 轴对称， 在 x 轴上取一点 H，连接 HF、HI、HG、GD、GE，则 HF＝HI…………① 设过 A、E 两点的一次函数解析式为：y＝kx＋b（k≠0）， ∵点 E 在抛物线上且点 E 的横坐标为 2，将 x＝2 代入抛物线 y＝－(x－1)2＋4，得 y＝－(2－1 )2＋4＝3 ∴点 E 坐标为（2，3） 又∵抛物线 y＝－(x－1)2＋4 图 像分别与 x 轴、y 轴交于点 A、B、D ∴当 y＝0 时，－(x－1)2＋4＝0，∴ x＝－1 或 x＝3 当 x＝0 时，y＝－1＋4＝3, ∴点 A（－1，0），点 B（3，0），点 D（0，3） 又∵抛物线的对称轴为：直线 x＝1， ∴点 D 与点 E 关于 PQ 对称，GD＝GE …………………② 分别将点 A（－1，0）、点 E（2，3）代入 y＝kx＋b，得： 解得： 过 A、E 两点的一次函数解析式为：y＝x＋1 ∴当 x＝0 时，y＝1 ∴点 F 坐标为（0，1） 9 2x < 0 2 3 k b k b − + =  + = 1 1 k b =  = 甲 地 乙 地 A 馆 3 台 15 台 B 馆 14 台 0 台 甲 地 乙 地 A 馆 4 台 14 台 B 馆 13 台 1 台 E F 图 6 A B x y O D C Q I G H P 出 发 地目 的 地 甲 地 乙 地 A 馆 x（台） _______（台） B 馆 _______（台）_______（台） 表 2 18－x 17－x x－3 ∴ ………………………………………③ 又∵点 F 与点 I 关于 x 轴对称， ∴点 I 坐标为（0，－1） ∴ ………④ 又∵要使四边形 DFHG 的周长最小，由于 DF 是一个定值， ∴只要使 DG＋GH＋HI 最小即可 由图形的对称性和①、②、③，可知， DG＋GH＋HF＝EG＋GH＋HI 只有当 EI 为一条直线时，EG＋ GH＋HI 最小 设过 E（2，3）、I（0，－1）两点的函数解析式为：y＝k1x＋b1（k1≠0）， 分别将点 E（2，3）、点 I（0，－1）代入 y＝k1x＋b1，得： 解得： 过 A、E 两点的一次函数解析式为：y＝2x－1 ∴当 x＝1 时，y＝1；当 y＝0 时，x＝ ； ∴点 G 坐标为（1，1），点 H 坐标为（ ，0） ∴四边形 DFHG 的周长最小为：DF＋DG＋GH＋HF＝DF＋EI 由③和④，可知： DF＋EI＝ ∴四边形 DFHG 的周长最小为 。 （ 3）如图 7，由题意可知，∠NMD＝∠MDB， 要使，△DNM∽△BMD，只要使 即可， 即：MD 2＝NM×BD………………………………⑤ 设点 M 的坐标为（a，0），由 MN∥BD，可得 △AMN∽△ABD， ∴ 再由（1）、（2）可知，AM＝1＋a，BD＝ ，AB＝4 ∴ ∵MD2＝OD2＋OM2＝a2＋9， ∴⑤式可写成： a2＋9＝ × 解得： a＝ 或 a＝3（不合题意，舍去） 2DF = 2 2 2 22 4 2 5EI DE DI= + = + = 1 1 1 2 3 1 k b b + =  = − 1 1 2 1 k b =  = − 1 2 1 2 2 2 5+ 2 2 5+ NM MD MD BD = NM AM BD AB = 3 2 (1 ) 3 2 3 2 (1 )4 4 AM BD aMN aAB × + ×= = = + 3 2 (1 )4 a+ 3 2 3 2 图 7 A B x y O D C M T N ∴点 M 的坐标为（ ，0） 又∵点 T 在抛物线 y＝－(x－1)2＋4 图像上， ∴当 x＝ 时，y＝ ∴点 T 的坐标为（ ， ） 3 2 3 2 15 4 3 2 15 4 深圳市 2012 年初中毕业生学业考试 数学试卷 说明：1、答题前，请将姓名、考生号、考场、试室号和座位号用规定的笔写在答题卡指定的位置上，将条形码粘贴好。 2、全卷分二部分，第一部分为选择题，第二部分为非选择题，共 4 页。考试时间 90 分钟，满分 100 分。 3、本卷试题，考生必须在答题卡上按规定作答；凡在试卷、草稿纸上作答的，其答案一律无效。答题卡必须保 持清洁，不能折叠。 4、本卷选择题 1—12，每小题选出答案后，用 2B 铅笔将答题卡选择题答题区内对应题目的答案标号涂黑，如需 改动，用橡皮擦干净后，再选涂其它答案；非选择题 13—23，答案（含作辅助线）必须用规定的笔，按作答 题目序号，写在答题卡非选择题答题区内。 5、考试结束，请将本试卷和答题卡一并交回 第一部分 选择题 1、 的倒数是（ ） A. B. C. D. 2、第八届中国（深圳）文博会以总成交额 143 300 000 000 元再创新高，将数 143 300 000 000 用科学计数法表示为（ ） A.。 B. C. D. 3、下列图形中，既是轴对称图形，又是中心对称图形的是（ ） 4、下列计算正确的是（ ） A. B. C. D. 5、在体育课上，某班两名同学分别进行了 5 次短跑训练，要判断哪一名同学的成绩比较稳定，通常要比较这两名学生 成绩的（ ） A. 平均数 B. 频数分布 C. 中位数 D. 方差 6、如图 1 所示，一个 角的三角形纸片，剪去这个 角后，得到 一个四边形，则 的度数为（ ） A. B. C. D. 7、端午节吃粽子是中华民族的传统习俗，妈妈买了 2 只红豆棕，3 只碱水粽，5 只感肉粽，粽子除内部馅料不同外其 它均相同，小颖随意吃一个，吃到红豆粽的概率是（ ） A. B. C. D. 8、下列命题： ① 方程 的解是 ② 4 的平方根是 2 ③ 有两边和一角相等的两个三角形全等 ④ 连接任意四边形各边中点的四边形是平行四边形 −3 3 −3 1 3 − 1 3 . × 101 433 10 . × 111 433 10 . × 121 433 10 . × 120 1433 10 a b ab+ =2 3 5 a a a• =2 3 5 ( )a a=3 32 6 a a a+ =6 3 9 60 60 ∠ + ∠1 2 120 180 240 300 1 10 1 5 1 3 1 2 x x=2 x = 1 A B C D 21 60° 图 1 x y C A OB M 图 2 A. 4 个 B. 3 个 C 2 个 D. 1 个 9、如图 2，⊙C 过原点，且与两坐标轴分别交于点 A，点 B，点 A 的坐标为（0，3），M 是第三象限内 上一点， ，则⊙C 的半径为（ ） A. 6 B. 5 C 3 D. 10、已知点 关于 轴的对称点在第一象限，则 的取值范围是（ ） A. B. C D. 11、小明想测一棵树的高度，他发现树的影子恰好落在地面和一斜坡上，如图 3，此时测得地面上的影长为 8 米，坡面 上的影长为 4 米，已知斜坡的坡角为 ，同一时刻，一根长为 1 米、垂直于地面放置的标杆在地面上的影长为 2 米，则树的高度为（ ） A. 米 B. 12 米 C 米 D. 10 米 12、如图 4，已知： ，点 、 、 ……在射线 上，点 、 、 ……在射线 上， 、 、 ……均为等边三角形，若 ，则 的边长为（ ） A. 6 B. 12 C 32 D. 64 第二部分 非选择题 二、填空题(本题共 4 小题, 每小题 3 分, 共 12 分) 13、分解因式： 。 14、二次函数 的最小值是 。 15、如图 5，双曲线 与⊙O 在第一象限内交于 、 两点，分别过 、 两点向 轴和 轴作垂线。 已知点 的坐标为（1，3）则图中阴影部分的面积为 。 16、如图 6，已知 中， ，以斜边 为边向外作正方形 ，且正方形的对角线交于点 ，连接 。已知 ， ，则另一直角边 的长为 。 OB BMO∠ = 120 3 2 ( , )1 2 3P a a+ − x a a < −1 a− < < 31 2 a− < <3 12 a > 3 2 30 ( )+6 3 ( )+4 2 3 MON∠ = 30 A1 A2 A3 ON B1 B2 B3 OM A B A∆ 1 1 2 A B A∆ 2 2 3 A B A∆ 3 3 4 OA =1 1 A B A∆ 6 6 7 a ab− =3 2 y x x= − +2 2 6 ( )ky kx = > 0 P Q P Q x y P Rt ABC∆ ACB∠ = 90 AB ABDE O OC AC = 5 OC = 6 2 BC 图 5 x y (1,3)P O 图 6 O D E A C B 图 4 N M B3 B2 B1 A4A3A2A1 O 图 3 30° 三、解答题（本题共 7 小题，其中第 17 题 5 分，第 18 题 6 分，第 19 题 7 分，第 20 题 8 分，第 21 题 8 分，第 29 题 9 分，第 23 题 9 分） 17、（5 分）计算： 18、（6 分）已知 ，求代数式 的值 19、（7 分）为了解 2012 年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况，随机调查了部分参赛同学的成 绩，整理并制作图表如下。 请根据以上图表提供的信息，解答下列问题： （1）本次调查的样本容量为 ； （2）在表中， ， ； （3）补全频数分布直方图； （4）参加比赛的小聪说，他的比赛成绩是所在抽查同学成绩的中位数，据此推测他的成绩落在 分数段内； （5）如果比赛成绩 80 分以上（含 80 分）为优秀，那么你估计该竞赛项目的优秀率大约是 。 20、（8 分）如图 7，将矩形 沿直线 折叠，使点 C 与点 A 重合，折痕交 AD 于点 E，交 BC 于点 F，连接 AF、CE， （1）求证：四边形 AFCE 为菱形； （2）设 请写出一个 、 、 三者之间的数量关系式 分 数 段 频数 频率 30 0.1 90 0.4 60 0.2 ( ) cos − − + − − −   2 014 3 1 8 452  ,a b= − =3 2 a ab b a b a b + + + ÷  +  2 21 1 2 m = n = ABCD EF , , ,AE a ED b DC c= = = a b c x <60 70≤ x <70 80≤ n x <80 90≤ m x90 100≤ ≤ ( D') ( C ') EA B C D F 图 7 21、（8 分）“节能环保，低碳生活”是我们倡导的一种 生活方式。某家电商场计划用 万元购进节能型电 视机、洗衣机和空调共 40 台。三种家电的进价及售价如右表所 示： （1）在不超出现有资金的前提下，若购进电视机的数量和洗衣机 的数量相同，空调的数量不超过电视机数量的三倍，请问商场有哪 几种进货方案？ （2）在“2012 年消费促进月”促销活动期间，商家针对这三种节能型产品推出“现金购满 1000 元送 50 元家电消费券 一张、多买多送”的活动，在（1）的条件下，若三种电器在活动期间全部售出，商家预计最多送出消费券多少张？ 22、（9 分）如图 8，已知△ABC 的三个顶点坐标分别为 （1）求经过 A、B、C 三点抛物线的解析式 （2）设直线 BC 交 y 轴于点 E，连接 AE，求证：AE=CE （3）设抛物线与 y 轴交于点 D，连接 AD 交 BC 于点 F，试问以 A、B、F 为顶点的三角形与△ABC 相似吗？请说明理 由。 23（9 分）如图 9—①，平在面直角从标系中，直线 的位置随 的不同取值而变化。 （1）已知⊙M 的圆心坐标为（4，2），半径为 2 当 时，直线 经过圆心 M； 当 时，直线 与 ⊙M 相切； （2）若把⊙M 换成矩形 ，如图 9—②，其三个顶点的坐标分别为： 。设直线 扫过矩 形 的面积为 ，当 由小到大变化时，请求出 与 的函数关系式。 进价（元/台） 售价（元/台） 电视机 5000 5500 洗衣机 2000 2160 空 调 2400 2700 .11 8 ( , ), ( , ), ( , )A B C− −4 0 1 0 2 6 : ( )l y x b b= − +2 0≥ b b = : ( )l y x b b= − +2 0≥ b = : ( )l y x b b= − +2 0≥ ABCD ( , ), ( , ), ( , )A B C2 0 6 0 6 2 l ABCD S b S b x y F E C D BA O 图 8 x y l: y = -2x+b M O 图 9—① 图 9—② x y l: y = -2x+b D C BAO