中考数学应用题专题复习 14页

‎2018年中考数学应用题专题复习 ‎1、整顿药品市场、降低药品价格是国家的惠民政策之一．根据国家《药品政府定价办法》，某省有关部门规定：市场流通药品的零售价格不得超过进价的15%．根据相关信息解决下列问题：‎ ‎（1）降价前，甲乙两种药品每盒的出厂价格之和为6.6元．经过若干中间环节，甲种药品每盒的零售价格比出厂价格的5倍少2.2元，乙种药品每盒的零售价格是出厂价格的6倍，两种药品每盒的零售价格之和为33.8元．那么降价前甲、乙两种药品每盒的零售价格分别是多少元？‎ ‎（2）降价后，某药品经销商将上述的甲、乙两种药品分别以每盒8元和5元的价格销售给医院，医院根据实际情况决定：对甲种药品每盒加价15%、对乙种药品每盒加价10%后零售给患者．实际进药时，这两种药品均以每10盒为1箱进行包装．近期该医院准备从经销商处购进甲乙两种药品共100箱，其中乙种药品不少于40箱，销售这批药品的总利润不低于900元．请问购进时有哪几种搭配方案？‎ ‎ ‎ ‎2、由于受金融危机的影响，某店经销的甲型号手机今年的售价比去年每台降价500元．如果卖出相同数量的手机，那么去年销售额为8万元，今年销售额只有6万元．‎ ‎（1）今年甲型号手机每台售价为多少元？‎ ‎（2）为了提高利润，该店计划购进乙型号手机销售，已知甲型号手机每台进价为1000元，乙型号手机每台进价为800元，预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台，请问有几种进货方案？‎ ‎（3）若乙型号手机的售价为1400元，为了促销，公司决定每售出一台乙型号手机，返还顾客现金a元，而甲型号手机仍按今年的售价销售，要使（2）中所有方案获利相同，a应取何值？‎ ‎3、为创建“国家卫生城市”，进一步优化市中心城区的环境，德州市政府拟对部分路段的人行道地砖、花池、排水管道等公用设施全面更新改造，根据市政建设的需要，须在60天内完成工程．现在甲、乙两个工程队有能力承包这个工程．经调查知道：乙队单独完成此项工程的时间比甲队单独完成多用25天，甲、乙两队合作完成工程需要30天，甲队每天的工程费用2500元，乙队每天的工程费用2000元．‎ ‎（1）甲、乙两个工程队单独完成各需多少天？‎ ‎（2）请你设计一种符合要求的施工方案，并求出所需的工程费用．‎ ‎4、某渔场计划购买甲、乙两种鱼苗共6000尾，甲种鱼苗每尾0.5元，乙种鱼苗每尾0.8元．相关资料表明：甲、乙两种鱼苗的成活率分别为90%和95%．‎ ‎（1）若购买这批鱼苗共用了3600元，求甲、乙两种鱼苗各购买了多少尾？‎ ‎（2）若购买这批鱼苗的钱不超过4200元，应如何选购鱼苗？‎ ‎（3）若要使这批鱼苗的成活率不低于93%，且购买鱼苗的总费用最低，应如何选购鱼苗？‎ ‎5、我国西南五省市的部分地区发生严重旱灾，为鼓励节约用水，某市自来水公司采取分段收费标准，右图反映的是每月收取水费y（元）与用水量x（吨）之间的函数关系.‎ ‎（1）小明家五月份用水8吨，应交水费______元；‎ ‎（2）按上述分段收费标准，小明家三、四月份分别交水费26元和18元，问四月份比三月份节约用水多少吨？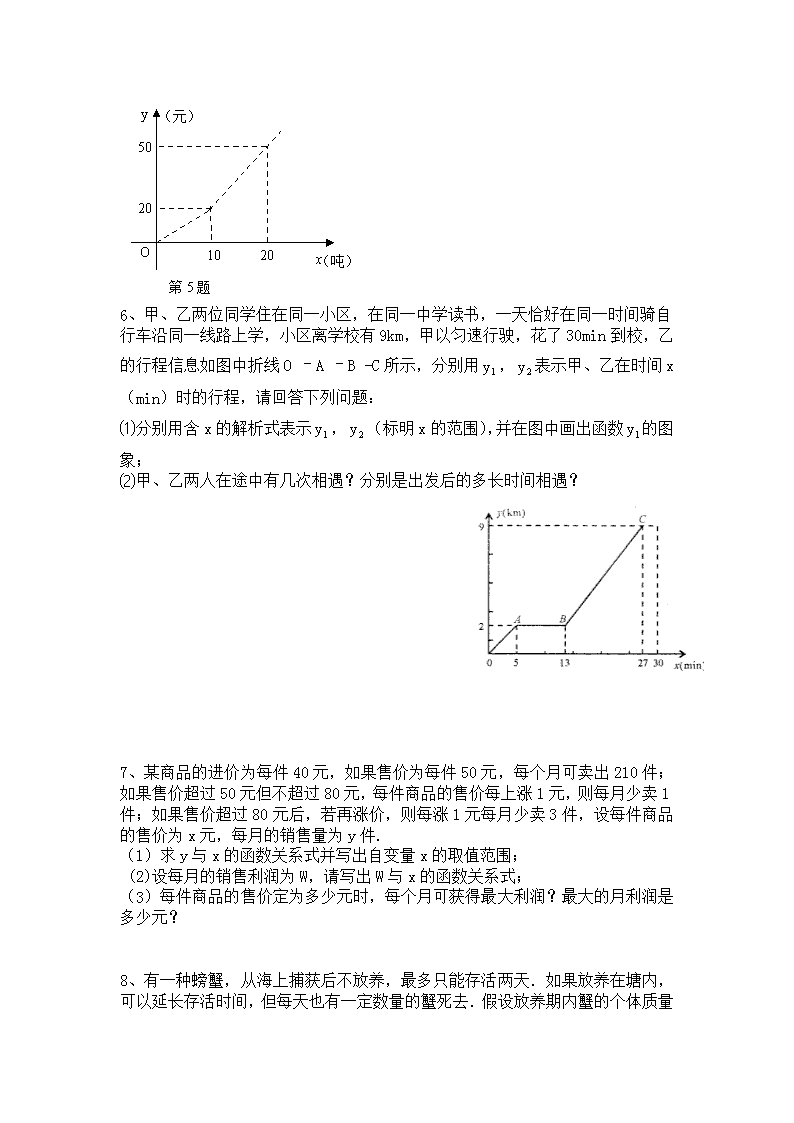‎ ‎ ‎O y x ‎20‎ ‎50‎ ‎10‎ ‎20‎ 第5题 ‎（吨）‎ ‎（元）‎ ‎ ‎ ‎6、甲、乙两位同学住在同一小区，在同一中学读书，一天恰好在同一时间骑自行车沿同一线路上学，小区离学校有9km，甲以匀速行驶，花了30min到校，乙的行程信息如图中折线O –A –B -C所示，分别用，表示甲、乙在时间x（min）时的行程，请回答下列问题：‎ ⑴分别用含x的解析式表示，（标明x的范围），并在图中画出函数的图象；‎ ⑵甲、乙两人在途中有几次相遇？分别是出发后的多长时间相遇？‎ ‎7、某商品的进价为每件40元，如果售价为每件50元，每个月可卖出210件；如果售价超过50元但不超过80元，每件商品的售价每上涨1元，则每月少卖1件；如果售价超过80元后，若再涨价，则每涨1元每月少卖3件，设每件商品的售价为x元，每月的销售量为y件.‎ ‎（1）求y与x的函数关系式并写出自变量x的取值范围；‎ ‎(2)设每月的销售利润为W，请写出W与x的函数关系式；‎ ‎（3）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？‎ ‎8、‎ 有一种螃蟹，从海上捕获后不放养，最多只能存活两天．如果放养在塘内，可以延长存活时间，但每天也有一定数量的蟹死去．假设放养期内蟹的个体质量基本保持不变，现有一经销商，按市场价收购这种活蟹1000 kg放养在塘内，此时市场价为每千克30元，据测算，此后每千克活蟹的市场价每天可上升1元，但是，放养一天需支出各种费用为400元，且平均每天还有10 kg蟹死去，假定死蟹均于当天全部销售出，售价都是每千克20元．‎ ‎(1)设x天后每千克活蟹的市场价为p元，写出p关于x的函数关系式；‎ ‎(2)如果放养x天后将活蟹一次性出售，并记1000 kg蟹的销售总额为Q元，写出Q关于x的函数关系式．‎ ‎(3)该经销商将这批蟹放养多少天后出售，可获最大利润(利润=Q－收购总额)？‎ ‎9、为打造“书香校园”，某学校计划用不超过1900本科技类书籍和1620本人文类书籍，组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本，人文类书籍50本；组建一个小型图书角需科技类书籍30本，人文类书籍60本．‎ ‎（1）问符合题意的组建方案有几种？请你帮学校设计出来；‎ ‎（2）若组建一个中型图书角的费用是860元，组建一个小型图书角的费用是570元，试说明在（1）中哪种方案费用最低？最低费用是多少元？‎ ‎10、 “保护环境，人人有责”为了更好的治理巴河，巴中市污水处理厂决定购买A、B两型污水处理设备，共10台，其信息如下表：‎ 单价(万元/台)‎ 每台处理污水量(吨/月)‎ A型 ‎12‎ ‎240‎ B型 ‎10‎ ‎200‎ ‎(1)设购买A型设备x台，所需资金共为W万元，每月处理污水总量为y吨，试写出W与x，y与x的函数关系式．‎ ‎(2)经预算，市污水处理厂购买设备的资金不超过106万元，月处理污水量不低于2040吨，请你列举出所有购买方案，并指出哪种方案最省钱，需要多少资金?‎ ‎11、某学校组织340名师生进行长途考察活动，带有行李170件，计划租用甲、乙两种型号的汽车共10辆．经了解，甲车每辆最多能载40人和16件行李，乙车每辆最多能载30人和20件行李．‎ ‎⑴请你帮助学校设计所有可行的租车方案；‎ ‎⑵如果甲车的租金为每辆2000元，乙车的租金为每辆1800元，问哪种可行方案使租车费用最省？‎ ‎12、莱芜盛产生姜，去年某生产合作社共收获生姜200吨，计划采用批发和零售两种方式销售.经市场调查，批发平均每天售出6吨．‎ ‎(1)受天气、场地等各种因素的影响，需要提前完成销售任务.在平均每天批发量不变的情况下，实际平均每天的零售量比原计划增加了2吨，结果提前5天完成销售任务.那么原计划零售平均每天售出多少吨？‎ ‎(2)在（1）条件下，若批发每吨获得的利润为2000元，零售每吨获得的利润为2200元，计算实际获得的总利润．‎ ‎13、某商场计划购进一批甲、乙两种玩具，已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元，用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同．‎ ‎（1）求每件甲种、乙种玩具的进价分别是多少元？‎ ‎（2）商场计划购进甲、乙两种玩具共48件，其中甲种玩具的件数少于乙种玩具的件数．商场决定此次进货的总资金不超过1000元，求商场共有几种进货方案？‎ ‎14、为了增强居民的节约用水的意识，某市制定了新的水费标准：每户每月用水量不超过5吨的部分，自来水公司按每吨2元收费；超过5吨的部分，按每吨2.6元收费。设某用户月用水量x吨，自来水公司的应收水费为y元。‎ ‎（1）试写出y（元）与x（吨）之间的函数关系式；‎ ‎（2）该户今年5月份的用水量为8吨，自来水公司应收水费多少元？ ‎ ‎15、一家蔬菜公司收购到某种绿色蔬菜140吨，准备加工后进行销售，销售后获利的情况如下表所示：‎ 销售方式 粗加工后销售 精加工后销售 每吨获利（元）‎ ‎1000‎ ‎2000‎ 已知该公司的加工能力是：每天能精加工5吨或粗加工15吨，但两种加工不能同时进行.受季节等条件的限制，公司必须在一定时间内将这批蔬菜全部加工后销售完.‎ ‎⑴如果要求12天刚好加工完140吨蔬菜，则公司应安排几天精加工，几天粗加工？‎ ‎⑵如果先进行精加工，然后进行粗加工.‎ ‎①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式；‎ ‎②若要求在不超过10天的时间内，将140吨蔬菜全部加工完后进行销售，则加工这批蔬菜最多可获得多少利润？此时如何分配加工时间？‎ ‎16、为迎接第四届世界太阳城大会，德州市把主要路段路灯更换为太阳能路灯．已知太阳能路灯售价为5000元/个，目前两个商家有此产品．甲商家用如下方法促销：若购买路灯不超过100个，按原价付款；若一次购买100个以上，且购买的个数每增加一个，其价格减少10元，但太阳能路灯的售价不得低于3500元/个．乙店一律按原价的80℅销售．现购买太阳能路灯x个，如果全部在甲商家购买，则所需金额为y1元；如果全部在乙商家购买，则所需金额为y2元.‎ ‎（1）分别求出y1、y2与x之间的函数关系式；‎ ‎（2）若市政府投资140万元，最多能购买多少个太阳能路灯？‎ ‎17、5月12日，我国四川省汶川县等地发生强烈地震，在抗震救灾中得知，甲、乙两个重灾区急需一种大型挖掘机，甲地需要25台，乙地需要23台；A、B两省获知情况后慷慨相助，分别捐赠该型号挖掘机26台和22台并将其全部调往灾区．如果从A省调运一台挖掘机到甲地要耗资0.4万元，到乙地要耗资0.3万元；从B省调运一台挖掘机到甲地要耗资0.5万元，到乙地要耗资0.2万元．设从A省调往甲地台挖掘机，A、B两省将捐赠的挖掘机全部调往灾区共耗资y万元．‎ ‎⑴请直接写出y与x之间的函数关系式及自变量x的取值范围；‎ ‎⑵若要使总耗资不超过15万元，有哪几种调运方案？‎ ‎⑶怎样设计调运方案能使总耗资最少？最少耗资是多少万元？‎ ‎18、一家计算机专买店A型计算器每只进价12元，售价20元，多买优惠：凡是一次买10只以上的，每多买一只，所买的全部计算器每只就降低0.10元，例如，某人买20只计算器，于是每只降价0.10×（20-10）＝1（元），因此，所买的全部20只计算器都按每只19元的价格购买．但是最低价为每只16元．‎ ‎（1）求一次至少买多少只，才能以最低价购买？‎ ‎（2）写出专买店当一次销售x（x＞10）只时，所获利润y元）与x（只）之间的函数关系式，并写出自变量x的取值范围；‎ ‎（3）一天，甲买了46只，乙买了50只，店主却发现卖46只赚的钱反而比卖50只赚的钱多，你能用数学知识解释这一现象吗？为了不出现这种现象，在其他优惠条件不变的情况下，店家应把最低价每只16元至少提高到多少？‎ 中考数学应用题专题答案 ‎1、（2010江苏盐城）‎ ‎【答案】解：（1）设甲种药品的出厂价格为每盒x元，乙种药品的出厂价格为每盒y元．‎ 则根据题意列方程组得： 解之得： ‎ ‎ 5×3.6-2.2=18-2.2=15.8（元） 6×3=18（元）‎ 答：降价前甲、乙两种药品每盒的零售价格分别是15.8元和18元 ‎（2）设购进甲药品x箱（x为非负整数），购进乙药品（100-x）箱，则根据题意列不等式组得：‎ ‎ 解之得： ‎ 则x可取：58，59，60，此时100-x的值分别是：42，41，40‎ 有3种方案供选择：第一种方案，甲药品购买58箱，乙药品购买42箱；‎ 第二种方案，甲药品购买59箱，乙药品购买41箱；‎ 第三种方案，甲药品购买60箱，乙药品购买40箱； ‎ ‎（注：（1）中不作答不扣分，（2）中在方案不写或写错扣1分）‎ ‎2、（2011广西梧州，24，10分）‎ ‎【答案】解：（1）设今年甲型号手机每台售价为x元，由题意得，‎ =． 解得x=1500． 经检验x=1500是方程的解．‎ 故今年甲型号手机每台售价为1500元．‎ ‎（2）设购进甲型号手机m台，由题意得，‎ ‎17600≤1000m+800（20－m）≤18400， 8≤m≤12．‎ 因为m只能取整数，所以m取8、9、10、11、12，共有5种进货方案．‎ ‎（3）方法一：‎ 设总获利W元，则W=（1500－1000）m+（1400－800－a）（20－m），‎ W=（a－100）m+12000－20a．‎ 所以当a=100时，（2）中所有的方案获利相同．‎ 方法二：‎ 由（2）知，当m=8时，有20－m=12．‎ 此时获利y1=（1500－1000）×8+（1400－800－a）×12=4000+（600－a）×12‎ 当m=9时，有20－m=11‎ 此时获利y2=（1500－1000）×9+（1400－800－a）×11=4500+（600－a）×11‎ 由于获利相同，则有y1= y2．即4000+（600－a）×12=4500+（600－a）×11，‎ 解之得a=100 ．所以当a=100时，（2）中所有方案获利相同．‎ ‎3、（2011山东德州21,10分）‎ 解：（1）设甲工程队单独完成需x天，则乙工程队单独完成该工程需（x+25）天．‎ 根据题意得：‎ ‎． ‎ 方程两边同乘以x（x+25），得 30（x+25）+30x= x（x+25），‎ ‎ 即 x2－35x－750=0． ‎ 解之，得x1=50，x2=－15． 经检验，x1=50，x2=－15都是原方程的解．‎ 但x2=－15不符合题意，应舍去． ∴ 当x=50时，x+25=75．‎ 答：甲工程队单独完成该工程需50天，则乙工程队单独完成该工程需75天．‎ ‎（2）此问题只要设计出符合条件的一种方案即可．‎ ‎ 方案一：‎ 由甲工程队单独完成． 所需费用为：2500×50=125000（元）．‎ 方案二：‎ ‎ 甲乙两队合作完成． 所需费用为：（2500+2000）×30=135000（元）．‎ 其它方案略．‎ ‎4、（2010四川眉山）‎ 解：（1）设购买甲种鱼苗x尾，则购买乙种鱼苗尾，由题意得：‎ ‎ 解这个方程，得： ∴‎ 答：甲种鱼苗买4000尾，乙种鱼苗买2000尾．‎ ‎（2）由题意得： 解这个不等式，得： ‎ 即购买甲种鱼苗应不少于2000尾．‎ ‎（3）设购买鱼苗的总费用为y，则 ‎ 由题意，有 解得： ‎ 在中 ∵，∴y随x的增大而减少 ‎∴当时，．‎ 即购买甲种鱼苗2400尾，乙种鱼苗3600尾时，总费用最低．‎ ‎5、（2010福建南平）‎ ‎【答案】解：（1）16；‎ ‎（2）解法一：由图可得 用水10吨内每吨2元，10吨以上每吨 =3元 三月份交水费26元>20元。所以用水：10+= 12（吨）‎ 四月份交水费18元<20元，所以用水：18÷2=9（吨）‎ ‎∴四月份比三月份节约用水：12－9= 3 （吨）‎ 解法二：由图可得 10吨内每吨2元，当y=18时，知x<10,∴x=18×=9 ‎ 当x≥10时，可设y与x的关系为：y=kx+b 由图可知，当x=10时,y=20;x=20时y=50 ，可解得 k=3,b=-10‎ ‎∴y与x之间的函数关系式为 y=3x－10‎ ‎∴ 当y=26时，知x>10 ,有26=3x－10，解得x=12‎ ‎∴ 四月份比三月份节约用水：12-9= 3 （吨）‎ ‎6、（2010湖北黄石）‎ ‎7、（1）y=260-x 505时，y＝10＋（ｘ－5）×2.6＝2.6ｘ－3‎ ‎（2）因为x＝8>5 所以y＝2.6×8－3=17.3．‎ ‎15、（2010四川内江）‎ ‎【答案】解：⑴设应安排x天进行精加工，y天进行粗加工，‎ 根据题意得： 解得 ‎ 答：应安排4天进行精加工，8天进行粗加工．‎ ‎⑵①精加工m吨，则粗加工（140－m）吨，根据题意得：‎ ‎ W＝2000m＋1000（140－m）＝1000m＋140000 .‎ ‎　②∵要求在不超过10天的时间内将所有蔬菜加工完，‎ ‎ ∴＋≤10 解得　m≤5. ∴0＜m≤5.‎ 又∵在一次函数W＝1000m＋140000中，k＝1000＞0， ∴W随m的增大而增大，‎ ‎∴当m＝5时，Wmax＝1000×5＋140000＝145000.　 ∴精加工天数为5÷5＝1，‎ 粗加工天数为（140－5）÷15＝9. ‎ ‎∴安排1天进行精加工，9天进行粗加工，可以获得最多利润为145000元．‎ ‎16、（2010 山东省德州）‎ ‎【答案】解：（1）由题意可知，‎ 当x≤100时，购买一个需元，故；‎ 当x≥100时，因为购买个数每增加一个，其价格减少10元，但售价不得低于3500元/个，所以x≤+100=250． ‎ 即100≤x≤250时，购买一个需5000-10(x-100)元，故y1=6000x-10x2；‎ 当x>250时，购买一个需3500元，故；‎ 所以， ‎ ‎． ‎ ‎(2) 当0