2018年初中数学突破中考压轴题几何模型之相似三角形中的一线三等角模型 7页

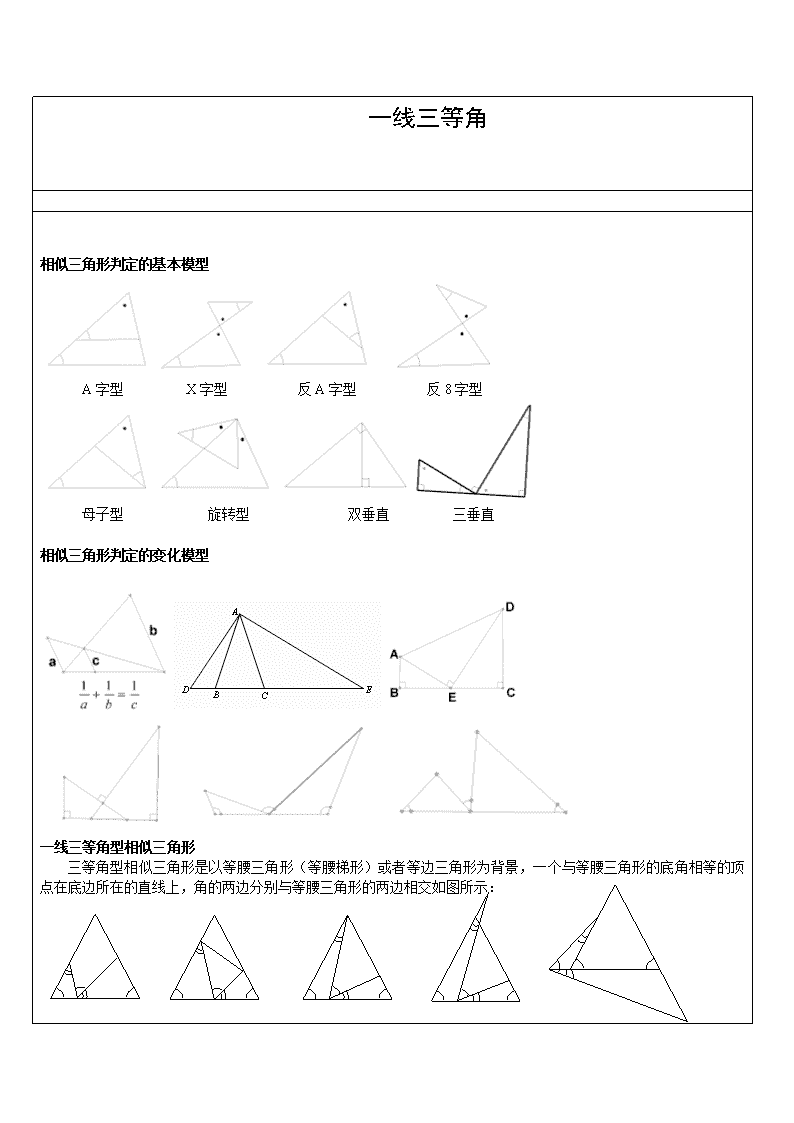
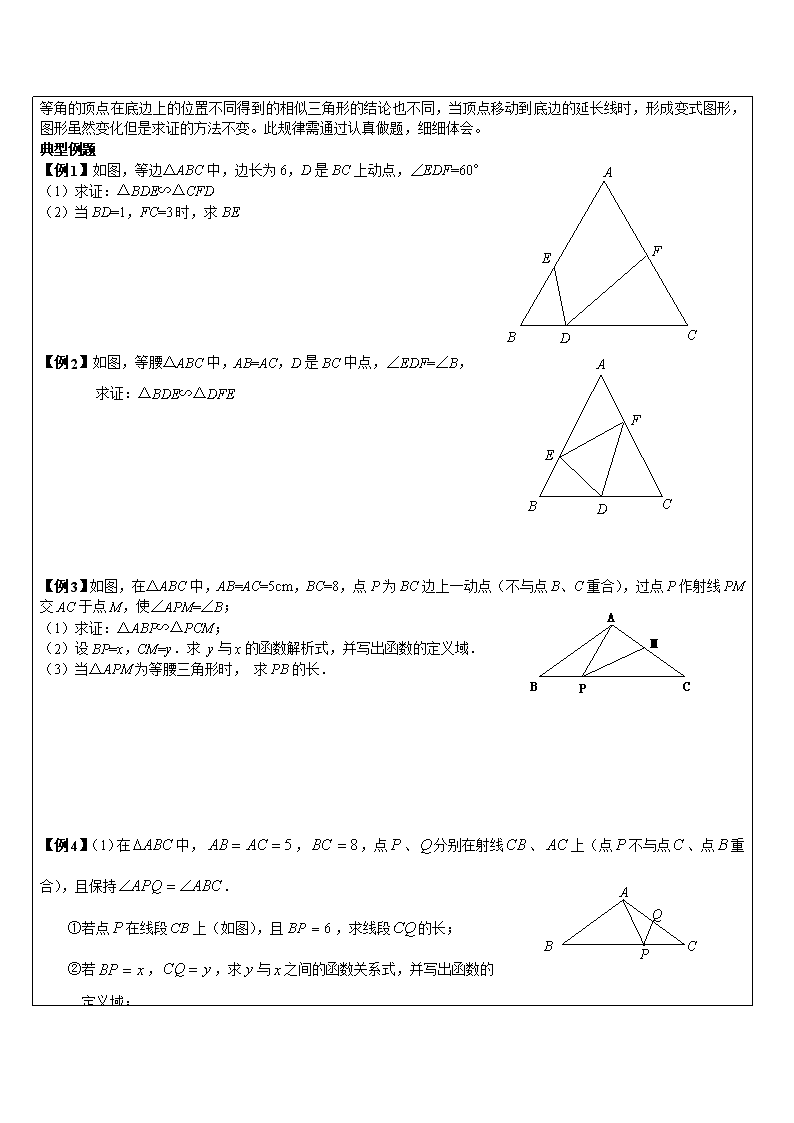
一线三等角 ‎ ‎ 相似三角形判定的基本模型 ‎ ‎ ‎ A字型 X字型 反A字型 反8字型 母子型 旋转型 双垂直 三垂直 相似三角形判定的变化模型 ‎ ‎ 一线三等角型相似三角形 三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景，一个与等腰三角形的底角相等的顶点在底边所在的直线上，角的两边分别与等腰三角形的两边相交如图所示：‎ 等角的顶点在底边上的位置不同得到的相似三角形的结论也不同，当顶点移动到底边的延长线时，形成变式图形，图形虽然变化但是求证的方法不变。此规律需通过认真做题，细细体会。‎ C A D B E F 典型例题 ‎【例1】如图，等边△ABC中，边长为6，D是BC上动点，∠EDF=60°‎ ‎（1）求证：△BDE∽△CFD ‎（2）当BD=1，FC=3时，求BE ‎ C D E A B F ‎【例2】如图，等腰△ABC中，AB=AC，D是BC中点，∠EDF=∠B，‎ 求证：△BDE∽△DFE A B P C M ‎【例3】如图，在△ABC中，AB=AC=5cm，BC=8，点P为BC边上一动点（不与点B、C重合），过点P作射线PM交AC于点M，使∠APM=∠B；‎ ‎（1）求证：△ABP∽△PCM；‎ ‎（2）设BP=x，CM=y．求 y与x的函数解析式，并写出函数的定义域．‎ ‎（3）当△APM为等腰三角形时， 求PB的长．‎ A B C P Q ‎【例4】（1）在中，，，点、分别在射线、上（点不与点、点重合），且保持.‎ ‎①若点在线段上（如图），且，求线段的长；‎ ‎②若，，求与之间的函数关系式，并写出函数的 ‎ 定义域；‎ ‎（2）正方形的边长为（如图12），点、分别在直线、上 ‎（点不与点、点重合），且保持.‎ A B C D 图12‎ 当时，写出线段的长（不需要计算过程，请直接写出结果）.‎ A B C 备用图 点评：此题是典型的图形变式题，记住口诀：“图形改变，方法不变”。动点在线段上时，通过哪两个三角形相似求解，当动点在线段的延长线上时，还是找原来的两个三角形，多数情况下这两个三角形还是相似的，还是可以沿用原来的方法求解。‎ ‎【例5】已知：菱形ABCD,AB=4m, ∠B=60°,点P、Q分别从点B、C出发，沿线段BC、CD以1m/s的速度向终点C、D运动,运动时间为t秒 ‎（1）连接AP、AQ、PQ，试判断△APQ的形状，并说明理由。‎ ‎（2）当t=1秒时，连接AC，与PQ相交于点K.求AK的长。‎ ‎（3） 当t=2秒时，连接AP、PQ,将∠APQ逆时针旋转，使角的两边与AB、AD、AC分别交于点E、N、F，连接EF.若AN=1,求S△EPF.‎ ‎ ‎ ‎【应用】‎ ‎1.如图，在平面直角坐标中，四边形OABC是等腰梯形，CB∥OA，OA=7，BC=1，AB=5，点P为x轴上的一个动点，点P不与点0、点A重合．连接CP，过点P作PD交AB于点D． （1）直接写出点B的坐标 ． ‎ ‎（2）当点P在线段OA上运动时，使得∠CPD=∠OAB，且BD: AD=3:2 ‎ ‎，求点P的坐标．‎ ‎2、已知在梯形ABCD中，AD∥BC，AD＜BC，且BC =6，AB=DC=4，点E是AB的中点．‎ ‎ （1）如图，P为BC上的一点，且BP=2．求证：△BEP∽△CPD；‎ ‎ （2）如果点P在BC边上移动（点P与点B、C不重合），且满足∠EPF=∠C，PF交直线CD于点F，同时交直线AD于点M，那么 ‎ ①当点F在线段CD的延长线上时，设BP=，DF=，求关于的函数解析式，并写出函数的定义域；②当时，求BP的长．‎ E D C B A ‎（备用图）‎ E D C B A P ‎（第25题图）‎ 模型训练：‎ A B C D E 1. 如图，在△ABC中，，，是边上的一个动点，点在边上，且．‎ ‎(1) 求证：△ABD∽△DCE；‎ ‎(2) 如果，，求与的函数解析式，并写出自变量的定义域；‎ ‎(3) 当点是的中点时，试说明△ADE是什么三角形，并说明理由．‎ 1. 已知：如图，在△ABC中，，，点D在边AB上，，点E在边BC上．又点F在边AC上，且．‎ ‎(1) 求证：△FCE∽△EBD；‎ ‎(2) 当点D在线段AB上运动时，是否有可能使．‎ 如果有可能，那么求出BD的长．如果不可能请说明理由．‎ 2. 如图，在△ABC中，AB=AC=5，BC=6，P是BC上一点，且BP=2，将一个大小与∠B相等的角的顶点放在P 点，然后将这个角绕P点转动，使角的两边始终分别与AB、AC相交，交点为D、E。‎ ‎（1）求证△BPD∽△CEP ‎（2）是否存在这样的位置，△PDE为直角三角形？‎ C P E A B D 若存在，求出BD的长；若不存在，说明理由。‎ A B C D E F 1. 如图，在△ABC中，AB=AC=5，BC=6，P是BC上的一个动点(与B、C不重合)，PE⊥AB与E，PF⊥BC交AC与F，设PC=x，记PE=，PF=‎ C P E A B F ‎（1）分别求、关于x的函数关系式 ‎（2）△PEF能为直角三角形吗?若能，求出CP的长，若不能，请说明理由。‎ 2. 已知在等腰三角形中，，是的中点， 是上的动点（不与、重合），连结，过点作射线，使，射线交射线于点，交射线于点.‎ ‎（1）求证：∽；‎ ‎（2）设.‎ ‎①用含的代数式表示；‎ ‎②求关于的函数解析式，并写出的定义域.‎ C D A B P 3. 已知在梯形ABCD中，AD∥BC，AD＜BC，且AD＝5，AB＝DC＝2．‎ ‎（1）如图8，P为AD上的一点，满足∠BPC＝∠A．‎ ‎①求证；△ABP∽△DPC ‎②求AP的长．‎ ‎（2）如果点P在AD边上移动（点P与点A、D不重合），且满足∠BPE＝∠A，PE交直线BC于点E，同时交直线DC于点Q，那么 ‎①当点Q在线段DC的延长线上时，设AP＝x，CQ＝y，求y关于x的函数解析式，并写出函数的定义域；‎ ‎②当CE＝1时，写出AP的长（不必写出解题过程）‎