毕节市2013年中考数学卷 7页

机密 启用前 毕节市2013年初中毕业生学业（升学）统一考试试卷 数 学 注意事项：‎ ‎1、答题前，务必将身己的姓名、准考证号填写在答题卡规定的位置。‎ ‎2、答题时，卷I 必须使用2B 铅笔，卷II必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置，字体工整，笔迹清楚。‎ ‎3、所有题目必须在答题卡上作答，在试卷上答题无效 ‎4、本试卷共6 页，满分150 分，考试用时150 分钟。‎ ‎5、考试结束后，将试卷和答题卡一并交回。‎ 卷 Ⅰ 一、选择题（本大题共15小题，每小题3分，共45分。在每小题的四个选项中，中只有一个选项正确。）‎ ‎1. -2的相反数是（ ）‎ ‎ A. ±2 B. 2 C. -2 D. ‎ ‎2.如图所示的几何体的主视图是：（ ）‎ 正面 A B C D ‎ ‎ ‎3. 2013年毕节市参加初中毕业学业（升学）统一考试的学生人数约为107000人，将107000用科学计数法表示为：（ ）‎ ‎ A. B. C. D. ‎ ‎4.实数（相邻两个1之间依次多一个0），其中无理数是（ ）个。‎ ‎ A. 1 B. 2 C. 3 D. 4 ‎ ‎5.估计的值在（ ）之间。‎ ‎ A. 1与2之间 B. 2与3之间 C. 3与4之间 D. 4与5之间 ‎6.下列计算正确的是（ ）‎ ‎ A. B. C. D. ‎ ‎7.已知等腰三角形的一边长为4，另一边长为8，则这个等腰三角形的周长为（ ）‎ ‎ A. 16 B. 20或16 C. 20 D. 12‎ ‎8.在下列图形中既是轴对称图形又是中心对称图形的是（ ）‎ ‎ ①线段 ②角 ③等边三角形 ④ 圆 ⑤平行四边形 ⑥矩形 ‎ A. ③④⑥ B.①③⑥ D.④⑤⑥ D. ①④⑥‎ ‎（第11题图）‎ ‎9.数据4, 7, 4, 8，6, 6, 9，4的众数和中位数是（ ）‎ ‎ A. 6，9 B. 4，8 C. 6, 8 D. 4, 6‎ ‎10. 分式方程的解是（ ）‎ ‎ A. B. C. D. 无解 ‎（第12题图）‎ ‎11.（2012•凉山州改编）如图，已知AB∥CD，∠EBA=45°，∠E+∠D的读数为（ ）‎ ‎ A. 30° B. 60° C. 90° D. 45°‎ ‎12.如图在⊙O中，弦AB=8，OC⊥AB，垂足为C，且OC=3，则⊙O的半径（ ）‎ ‎ A. 5 B. 10 C. 8 D. 6‎ ‎（第13题图）‎ ‎13.一次函数与反比例函数的图像在同一直角坐标系下的大致图像如图所示，则k、b的取值范围是（ ）‎ ‎ A. B. C. D. ‎ ‎14. 将二次函数的图像向右平移一个单位长度，再向上平移3个单位长度所得的图像解析式为（ ）‎ ‎ A. B. ‎ ‎ C. D. ‎ ‎（第15题图）‎ E A B D C M O N ‎15.在等腰直角三角形ABC中，AB=AC=4，点O为BC的中点，以O为圆心作⊙O交BC于点M、N，⊙O与AB、AC相切，切点分别为D、E，则⊙O的半径和∠MND的度数分别为（ ）‎ ‎ A. 2 , 22.5° B. 3 , 30° C. 3 , 22.5° D. 2 , 30°‎ ‎ ‎ 卷 Ⅱ 二、填空题（本大题共5个小题，每小题5分，共25分）‎ ‎16.二元一次方程组的解是 。‎ ‎17.正八边形的一个内角的度数是 度。‎ ‎18.已知⊙O1与⊙O2的半径分别是、，且、满足，圆心距则两圆的位置关系是 。‎ ‎19.已知圆锥的底面半径是2cm,母线长为5cm，则圆锥的侧面积是 （结果保留π）‎ ‎20.一次函数的图像经过（1，2），则反比例函数的图像经过点（2， )。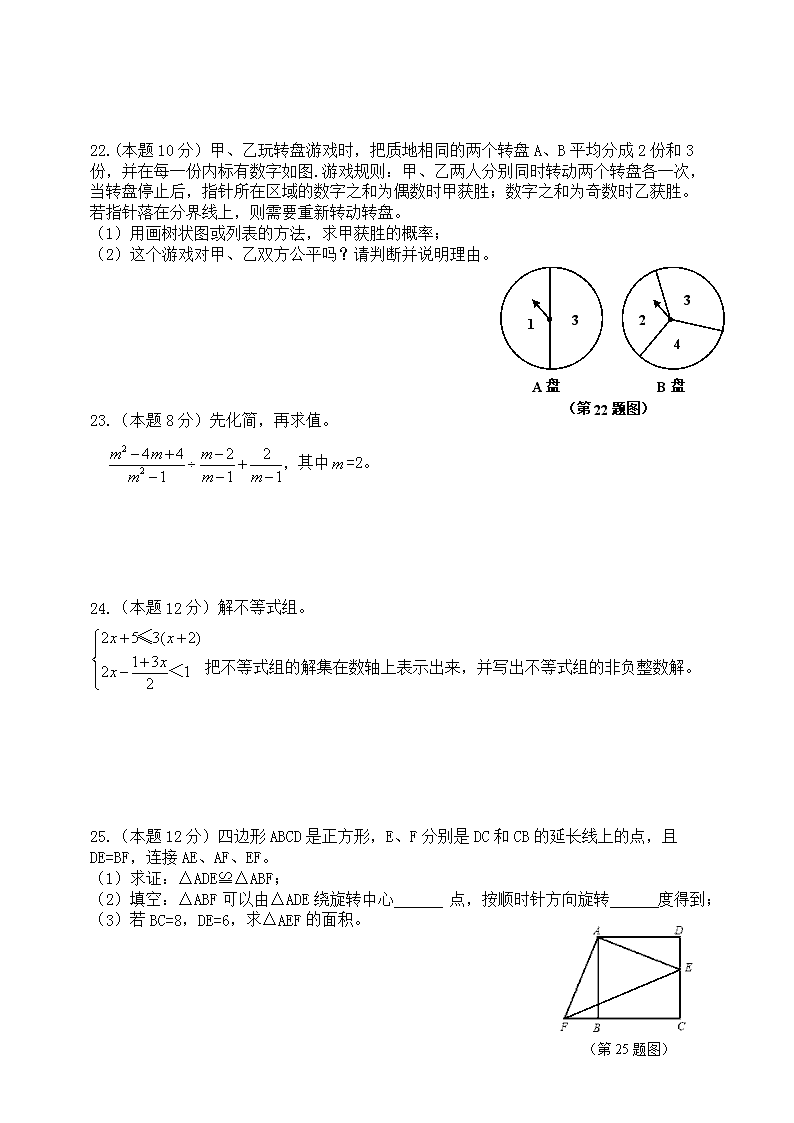‎ 三、解答及证明（本大题共7个小题，各题的分值见题号，共80分）‎ ‎21.（本题8分）计算：‎ ‎ ‎ ‎22.(本题10分）甲、乙玩转盘游戏时，把质地相同的两个转盘A、B平均分成2份和3份，并在每一份内标有数字如图.游戏规则：甲、乙两人分别同时转动两个转盘各一次，当转盘停止后，指针所在区域的数字之和为偶数时甲获胜；数字之和为奇数时乙获胜。若指针落在分界线上，则需要重新转动转盘。‎ ‎（1）用画树状图或列表的方法，求甲获胜的概率；‎ ‎（2）这个游戏对甲、乙双方公平吗？请判断并说明理由。‎ ‎（第22题图）‎ ‎1‎ ‎3‎ ‎2‎ ‎4‎ ‎3‎ A盘 B盘 ‎23.（本题8分）先化简，再求值。‎ ‎ 其中=2。‎ ‎24.（本题12分）解不等式组。‎ 把不等式组的解集在数轴上表示出来，并写出不等式组的非负整数解。‎ ‎25.（本题12分）四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF。‎ ‎（1）求证：△ADE≌△ABF；‎ ‎（2）填空：△ABF可以由△ADE绕旋转中心 点，按顺时针方向旋转 度得到；‎ ‎（第25题图）‎ ‎（3）若BC=8，DE=6，求△AEF的面积。‎ ‎（第26题图）‎ B A E D C ‎26.（本题14分） 如图，小明为了测量小山顶的塔高，他在A处测得塔尖D的仰角为45°，再沿AC方向前进73.2米到达山脚B处，测得塔尖D的仰角为60°，塔底E的仰角为30°，求塔高。（精确到0.1米，）‎ ‎27.（本题16分）如图，抛物线与轴交于点A、B，且A点的坐标为（1,0），与y轴交于点C（0，1）。‎ ‎（1）求抛物线的解析式，并求出点B坐标；‎ ‎（2）过点B作BD∥CA交抛物线与点D，连接BC、CA、AD，求四边形ABCD的周长；（结果保留根号）‎ ‎（3）在轴上方的抛物线上是否存在点P，过点P作PE垂直于轴，垂足为点E，是以B、P、E为顶点的三角形与△CBD相似，若存在请求出P点的坐标；若不存在，请说明理由。‎ 毕节市2013年初中毕业生学业（升学）统一考试数学试题 参考答案 卷 Ⅰ 一、选择题（每小题3分，共45分。）‎ ‎1.B 2.C 3.B 4.B 5.C 6.C 7.C 8.D 9.D 10. C 11.D 12.A 13.C 14. C 15.A ‎ 卷 Ⅱ 二、填空题（每小题5分，共25分）‎ ‎16.=3，=-1 。17. 135 。18. 外切 。19. 10π 20. 。‎ 三、解答及证明（本大题共7个小题，各题的分值见题号，共80分）‎ ‎21.（本题8分）‎ 解：原式=1+5+2-3-2=3‎ ‎（第22题图）‎ ‎1‎ ‎3‎ ‎2‎ ‎4‎ ‎3‎ A盘 B盘 开始始 转盘A： 1 3‎ 转盘B： 2 3 4 2 3 4‎ 数字和： 3 4 5 5 6 7‎ ‎22.(本题10分）‎ 解：画树状图如下：‎ 由上图可知，所有出现的可能情况有3、4、5、5、6、7六种。‎ 所以，P（甲获胜）==；P（乙获胜）==；‎ 由于＜，即P（甲获胜）＜P（乙获胜），因此这个游戏对甲、乙双方不公平。‎ ‎23.（本题8分）‎ 解：原式===‎ ‎ =‎ ‎ 当=2时，原式===2‎ ‎24.（本题12分）‎ ①‎ ②‎ 解：‎ 解不等式①得：≥-1，解不等式②得：＜3.‎ 所以原不等式组的解集是: -1≤＜3‎ 其解集在数轴上表示如下：‎ 所以不等式组的非负整数解有：0、1、2。‎ ‎（第25题图）‎ ‎25.（本题12分）‎ ‎（1）证明：∵ 四边形ABCD是正方形，F是BC延长线上一点，‎ ‎ ∴ AB=AD,∠ABF=∠D=90°‎ ‎ 又∵ DE=BF ‎ ∴ △ADE≌△ABF （SAS）‎ ‎ （3）解：由（1）△ADE≌△ABF可得∠FAB=∠EAD,AE=AF ‎ ∴ ∠FAB+∠BAE=∠EAD+∠BAE ‎ 即 ∠FAE=∠BAD=90°，△AEF为等腰直角三角形。‎ ‎ ∴ S△AEF =AE●AF=AE●AE=AE2.‎ ‎ 若BC=8，DE=6,则AD=BC=8，AE==10‎ ‎ S△AEF=AE2 =×102 =50 （平方单位）‎ ‎（第26题图）‎ B A E D C ‎ 答：△AEF的面积为50平方单位。‎ ‎26.（本题14分）‎ 解：∵ 在山脚B处测得塔尖D的仰角为60°，塔底E的仰角为30°。‎ ‎ ∴ ∠DBC = 60°,∠EBC= 30°‎ ‎ ∴ ∠DBE = ∠DBC -∠EBC=60°- 30°= 30°‎ ‎ 又∵ ∠BCD=90°‎ ‎ ∴ ∠BDC = 90°-∠DBC = 90°-60°= 30°‎ ‎ 即 ∠BDE = 30°‎ ‎ ∴ ∠BDE =∠DBE ,BE=DE.‎ ‎ 设EC=，则BE=2EC=2，BC=‎ ‎ DE=BE=2，DC=EC+DE=+2=3‎ ‎ 又∵ 在A处测得塔尖D的仰角为45°，AB=73.2‎ ‎ ∴ △ACD为等腰Rt△，即AC=DC=3,BC=AC-AB=3-73.2‎ ‎ ∴ =3-73.2，即1.732=3-73.2，2.268=73.2，≈32.3（米）‎ ‎27.（本题16分）‎ 解：（1）因为A（1,0），C（0，1）在抛物线上，‎ 将=1，y=0和=0，y=1分别代入解得：=-1，b=1‎ 即抛物线解析式为：‎ 因为抛物线的对称轴为y轴，所以B与A关于y轴对称，即B（-1，0）‎ ‎（2）过D作DE⊥轴于点E，‎ ‎ 因为D点在抛物线上，设D（，），‎ ‎ 即OE=,DE=||‎ ‎ 因为A（1,0），B（-1，0），C（0，1）‎ ‎ 所以OA=OB=OC=1，△AOC、△BOC、△ABC为等腰Rt△，‎ ‎ AC=BC==，∠CAB=45°。‎ ‎ 由BD∥CA得：∠DBE=∠CAB=45°,BE=DE ‎ 因为BE=OE+OB=+1，所以||=+1，‎ ‎ 由于D在第四象限，2-1=+1，解之得1=-1（不合题意，舍去），2=2 .‎ ‎ 所以D（2，-3），BE=DE=3，BD=‎ 又因为AE=OE-OA=2-1=1，所以AD=‎ 即四边形ABCD的周长为：AC+BC+BD+AD=++3+=5+‎ ‎（3）存在。求解过程如下：‎ ‎ 设P（，），其中 -1＜＜1,由此可得：BE=+1，EP=‎ 由（2）知∠CBD=∠DBE+∠ABC=45°+45°=90°,即△CBD为Rt△.‎ 当以B、P、E为顶点的三角形与△CBD相似时，主要有下列两种情况：‎ ① Rt△BEP∽Rt△CBD时，.‎ 由（2）知，CB=,BD=3,即，‎ 化简整理得：2+3+2=0，解之得：1= -1 ，2= -2 （均不合题意，舍去）‎ 此时无符合条件的P点坐标。‎ ② Rt△PEB∽Rt△CBD时，.‎ 由（2）知，CB=,BD=3,即，‎ 化简整理得：32 +-2=0，解之得：1= -1 （均不合题意，舍去），2= ‎ 此时符合条件的P点坐标为(,)‎ 综上所述，符合条件的P点坐标为(,)‎