- 297.00 KB
- 2021-05-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2004年河北省初中生统一考试
数学试卷
本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题.
本试卷满分为120分,考试时间为120分钟.
卷Ⅰ(选择题,共20分)
注意事项:1. 答卷Ⅰ前,考生务必将自己的姓名、准考证号、科目填涂在答题卡上,考试结束,监考人员将试卷和答题卡一并收回.
2. 每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.答在试卷上无效.
一、选择题(本大题共10个小题;每小题2分,共20分.在每小题给出的四个选项中,只
有一项是符合题目要求的)
1. 2的倒数是
A. B. C. D.
2. 第五次全国人口普查结果显示,我国的总人口已达到1300000000人,用科学记数法表
示这个数,正确的是
A.1.3×108 B.1.3×109 C.0.13×1010 D.13×109
3. 化简,结果正确的是
A. B. C. D.
4. 若x1,x2是一元二次方程2x2-3x+1=0的两个根,则的值是
A. B. C. D.
R1
R2
图1
5. 图1所示的电路的总电阻为10Ω,若R1=2R2,则R1,R2的值分别是
A.R1=30Ω,R2=15Ω B.R1=Ω,R2=Ω
C.R1=15Ω,R2=30Ω D.R1=Ω,R2=Ω
4号袋
2号袋
图3
3号袋
1号袋
6. 图2是一个经过改造的台球桌面的示意图,图中四个角上的阴影
部分分别表示四个入球孔.如果一个球按图中所示的方向被击出
(球可以经过多次反射),那么该球最后将落入的球袋是
A.1 号袋 B.2 号袋
C.3 号袋 D.4 号袋
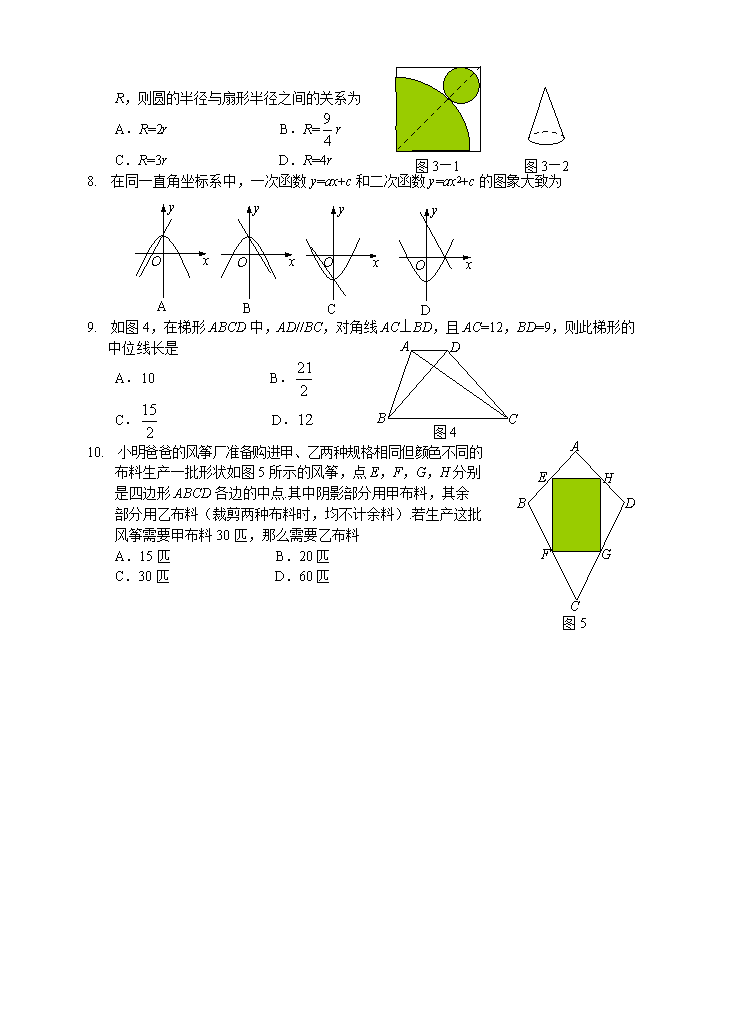
7. 如图3—1,在正方形铁皮上剪下一个圆形和扇形,使之恰好围
成图3—2所示的一个圆锥模型.设圆的半径为r,扇形半径为
图3—2
图3—1
R,则圆的半径与扇形半径之间的关系为
A.R=2r B.R=r
C.R=3r D.R=4r
8. 在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为
x
y
O
B
x
y
O
D
y
O
C
x
y
O
A
x
A
C
D
图4
B
9. 如图4,在梯形ABCD中,AD//BC,对角线AC⊥BD,且AC=12,BD=9,则此梯形的
中位线长是
A. B.
A
E
H
D
F
G
B
C
图5
C. D.
10. 小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同的
布料生产一批形状如图5所示的风筝,点E,F,G,H分别
是四边形ABCD各边的中点.其中阴影部分用甲布料,其余
部分用乙布料(裁剪两种布料时,均不计余料).若生产这批
风筝需要甲布料30匹,那么需要乙布料
A.15匹 B.20匹
C.30匹 D.60匹
2004年河北省初中生升学统一考试
数学试卷
卷Ⅱ(非选择题,共100分)
注意事项:1. 答卷Ⅱ前,将密封线左侧的项目填写清楚.
2. 答卷Ⅱ时,将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.
二、填空题(本大题共10个小题;每小题2分,共20分.把答案写在横线上)
11. -|-8|的值是 .
12. 已知,则的余角等于 .
13. 不等式组的解集是 .
14. 分解因式:x2+2xy+y2-4= .
15. 若将二次函数y=x2-2x+3配方为y=(x-h)2+k的形式,则y= .
16. 用换元法解分式方程时,如果设,那么原方程可化为关于y的一元二次方程的一般形式是 .
A
D
C
B
图6
17. 如图6,若将四根木条钉成的矩形木框变形为平行四边形ABCD
的形状,并使其面积为矩形面积的一半,则这个平行四边形的
一个最小内角的值等于 .
60
120
140
B
60
A
C
图7
18. 若反比例函数的图象过点(3,-4),则此函数的解析式为 .
19. 图7是一个外轮廓为矩形的机器零件平面示意图,根据图中标出
尺寸(单位:mm)计算两圆孔中心A和B的距离为 .
20. 扑克牌游戏
小明背对小亮,让小亮按下列四个步骤操作:
第一步 分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌的张数相同;
第二步 从左边一堆拿出两张,放入中间一堆;
第三步 从右边一堆拿出一张,放入中间一堆;
第四步 左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.
这时,小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌的张数是 .
三、解答题(本大题共8个小题;共80分.解答应写出文字说明、证明过程或演算步骤)
21. (本小题满分8分)
已知,求的值.
22. (本小题满分8分)
A
D
B
F
E
C
图8
已知:如图8,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF.
求证:DE=BF.
23. (本小题满分8分)
为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动.
初中三个年级根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分为100分)如下表所示:
决赛成绩(单位:分)
初一年级
80 86 88 80 88 99 80 74 91 89
初二年级
85 85 87 97 85 76 88 77 87 88
初三年级
82 80 78 78 81 96 97 88 89 86
(1)请你填写下表:
平均数
众数
中位数
初一年级
85.5
87
初二年级
85.5
85
初三年级
84
(2)请从以下两个不同的角度对三个年级的决赛成绩进行分析:
① 从平均数和众数相结合看(分析哪个年级成绩好些);
② 从平均数和中位数相结合看(分析哪个年级成绩好些).
(3)如果在每个年级参加决赛的选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一些?并说明理由.
24. (本小题满分8分)
如图9—1,一个圆球放置在V形架中.图9—2是它的平面示意图,CA和CB都是⊙O
的切线,切点分别是A,B.如果⊙O的半径为cm,且AB=6cm,求∠ACB.
图9—1
图9—2
A
O
B
C
25. (本小题满分12分)
x
x
y
图10—1
如图10—1是某段河床横断面的示意图.查阅该
河段的水文资料,得到下表中的数据:
x(米)
5
10
20
30
40
50
y(米)
0.125
0.5
2
4.5
8
12.5
O
10
20
30
40
50
60
x(米)
2
14
12
10
8
6
4
y(米)
图10—2
(1)请你以上表中的各对数据(x,y)作为点的坐标,
尝试在图10—2所示的坐标系中画出y关于x的
函数图象;
(2)①填写下表:
x
5
10
20
30
40
50
②根据所填表中数据呈现的规律,猜想出用x表示y
的二次函数的表达式: .
(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能
否在这个河段安全通过?为什么?
26. (本小题满分12分)
图11—1
我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图11—1).
探索下列问题:
(1)在图11—2给出的四个正方形中,各画出一
条直线(依次是:水平方向的直线、竖直方
图11—2
向的直线、与水平方向成45°角的直线和
任意的直线),将每个正方形都分割成面积
m
m
m
m
图11—3
相等的两部分;
(2)一条竖直方向的直线m以及任意的直线n,
在由左向右平移的过程中,将正六边形分成
左右两部分,其面积分别记为S1和S2.
①请你在图11—3中相应图形下方的横线上
n
图11—4
分别填写S1与S2的数量关系式(用“<”,
“=”,“>”连接);
②请你在图11—4中分别画出反映S1与S2
三种大小关系的直线n,并在相应图形下
方的横线上分别填写S1与S2的数量关系
式(用“<”,“=”,“>”连接).
图11—5
(3)是否存在一条直线,将一个任意的平面图形(如图11—5)分割成面积相等的两部分?请简略说出理由.
27. (本小题满分12分)
光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.
两地区与该农机租赁公司商定的每天的租赁价格见下表:
每台甲型收割机的租金
每台乙型收割机的租金
A地区
1800元
1600元
B地区
1600元
1200元
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说
明有多少种分派方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提
出一条合理建议.
28. (本小题满分12分)
A
G
D
B
F
C
O
E
H
图12
已知:如图12,等边三角形ABC的边长为6,点D,E分别在边AB,AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.
(1)设△EGA的面积为S,写出S与t的函数关系式;
(2)当t为何值时,AB⊥GH;
(3)请你证明△GFH的面积为定值;
(4)当t为何值时,点F和点C是线段BH的三等分点.
2004年河北省初中生升学统一考试
数学试题参考答案及评分标准
说明:
1. 各地阅卷过程中,如考生还有其它正确解法,可参照评分标准步骤酌情给分.
2. 坚持每题评阅到底的原则,当考生的解答在某一步出现错误,影响了后继部分时,如果该
步以后的解答未改变这一题的内容和难度,可视影响的程度决定后面部分的给分,但不
超过后继部分给分数的一半;如果这一步后面的解答有较严重的错误,就不给分.
3. 解答右端所注分数,表示正确做到这一步应得的累加分数.
4. 只给整数分数.
一、选择题(每小题2分,共10分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
B
D
A
A
B
D
B
C
C
二、填空题(每小题2分,共20分)
11. -8;12. 22°;13. 2S2
S1S2
②
①
26. (本小题共12分)
(1) ………………………………2分
(2) ………………………………………………5分
…………………………………………8分
(3)存在. …………………………………………10分
对于任意一条直线l ,在直线l从平面图形的一侧向另一侧平移的过程中,当图形被直线l分割后,设直线l两侧图形的面积分别为S1,S2.两侧图形的面积由S1S2)的情形,逐渐变为S1>S2(或S1