中考数学一轮复习专题全等三角形能力提升 5页

‎《全等三角形》能力提升 一 选择题：‎ ‎1.下列命题中：‎ ‎（1）形状相同的两个三角形是全等形；‎ ‎（2）在两个全等三角形中，相等的角是对应角，相等的边是对应边；‎ ‎（3）全等三角形对应边上的高、中线及对应角平分线分别相等，其中真命题的个数有（　 　）‎ ‎ A．3个  B．2个  C．1个  D．0个 ‎2. 、如图，已知△ABC≌△ADE，∠D=55°，∠AED=76°，则∠C的大小是（　 　）‎ ‎ ‎ ‎ A．50° B．6O° C．76° D．55°‎ ‎3.下列各组图形中，是全等形的是（     ）‎ ‎ A.两个含60°角的直角三角形；      B.腰对应相等的两个等腰直角三角形；‎ ‎ C.边长为3和5的两个等腰三角形；    D.一个钝角相等的两个等腰三角形 ‎4.如图，△ABD≌△ACE，∠AEC=110°，则∠DAE的度数为（     ）‎ ‎ ‎ ‎ A．30°         B．40°         C．50°        D．60°‎ ‎5. 如图，P是等边三角形ABC内的一点，且PA=3，PB=4，PC=5，以BC为边在△ABC外作△BQC△BPA，连接PQ，则以下结论错误的是（ ）‎ ‎ A. △BPQ是等边三角形    B. △PCQ是直角三角形 C. APB=150°  D. APC=135°‎ ‎ ‎ ‎6. 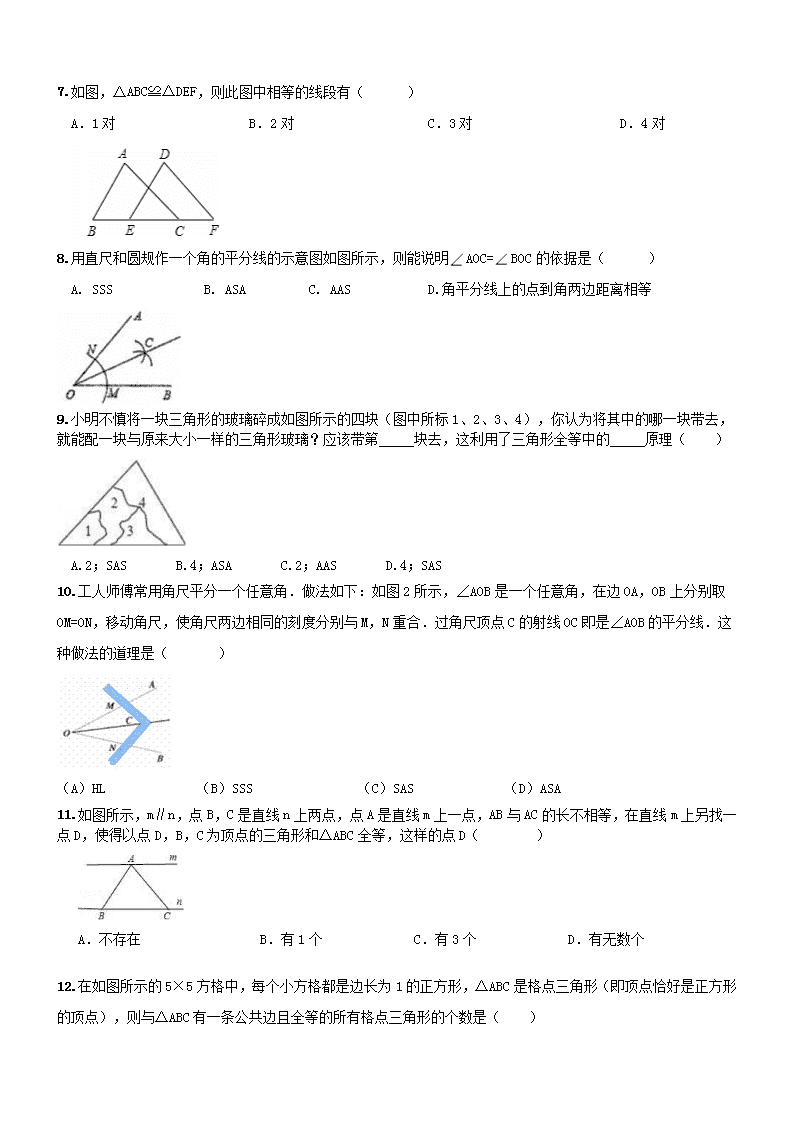如图，点E、F在AC上，AD=BC，DF=BE，要使△ADF≌△CBE，还需要添加一个条件是（　　）‎ ‎ ‎ ‎ A．AD∥BC    B．DF∥BE     C．∠D=∠B  D．∠A=∠C ‎7.如图，△ABC≌△DEF，则此图中相等的线段有（　 　）‎ ‎ A．1对          B．2对          C．3对           D．4对 ‎ ‎ ‎8.用直尺和圆规作一个角的平分线的示意图如图所示，则能说明AOC=BOC的依据是（ ）‎ ‎ A. SSS      B. ASA     C. AAS     D.角平分线上的点到角两边距离相等 ‎ ‎ ‎9.小明不慎将一块三角形的玻璃碎成如图所示的四块（图中所标1、2、3、4），你认为将其中的哪一块带去，就能配一块与原来大小一样的三角形玻璃？应该带第_____块去，这利用了三角形全等中的_____原理（　　）‎ ‎ A.2；SAS    B.4；ASA    C.2；AAS    D.4；SAS ‎10.工人师傅常用角尺平分一个任意角．做法如下：如图2所示，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合．过角尺顶点C的射线OC即是∠AOB的平分线．这种做法的道理是（    ）‎ ‎（A）HL       （B）SSS        （C）SAS       （D）ASA ‎11. 如图所示，m∥n，点B，C是直线n上两点，点A是直线m上一点，AB与AC的长不相等，在直线m上另找一点D，使得以点D，B，C为顶点的三角形和△ABC全等，这样的点D（　 　）‎ ‎ ‎ ‎ A．不存在      B．有1个      C．有3个     D．有无数个 ‎12. 在如图所示的5×5方格中，每个小方格都是边长为1的正方形，△ABC是格点三角形（即顶点恰好是正方形的顶点），则与△ABC有一条公共边且全等的所有格点三角形的个数是（　　）‎ ‎ A．1     B．2    C．3    D．4‎ ‎13. 如图，在线段AE同侧作两个等边三角形△ABC和△CDE（∠ACE＜120°），点P与点M分别是线段BE和AD的中点，则△CPM是（　　）‎ ‎ A．钝角三角形    B．直角三角形   C．等边三角形   D．非等腰三角形 二 填空题:‎ ‎14、如果∆ABC≌ ∆ADC，AB=AD， ∠B=70°,BC=‎3cm,那么∠D=____,DC=__cm ‎15、△ABC≌△DEF，且△ABC的周长为12，若AB=3，EF=4，则AC=        ．‎ ‎16、如图，AD是△ABC的角平分线，DE⊥AB，垂足为E，若△ABC的面积为9，DE=2，AB=5，则AC长是　　 ．                                          ‎ ‎ ‎ ‎17、如图,已知△ABC的周长是21,OB，OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC面积是　　 ．‎ ‎ ‎ ‎18.如图，在△ABC中，AB=5，AC=3，AD、AE分别为△ABC的中线和角平分线，过点C作CH⊥AE于点H，并延长交AB于点F，连结DH，则线段DH的长为　　　　　　．‎ ‎　‎ ‎19.如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：①∠BOC=90º＋∠A； ②EF=BE+CF；③设OD=m，AE＋AF=n，则S△AEF=mn； ‎ ‎④EF是△ABC的中位线．其中正确的结论是              ．‎ 三 简答题：‎ ‎20.如图所示，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点．‎ ‎（1）求证：△BCD≌△ACE；（2）若AE=8，DE=10，求AB的长度．‎ ‎21. 如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D．求证：‎ ‎（1）△BEC≌△CDA；（2）DE=AD﹣BE．‎ ‎22.如图，M是△ABC的边BC的中点，AN平分∠BAC，BNAN于点N，延长BN交AC于点D，已知AB=10，BC=15，MN=3.‎ ‎（1）求证：BN=DN；（2）求△ABC的周长.‎ ‎23.已知：如图1，点A是线段DE上一点，∠BAC=90°，AB=AC，BD⊥DE，CE⊥DE，           ‎ ‎（1）求证：DE=BD+CE； （2）如果是如图2这个图形，我们能得到什么结论？并证明．             ‎ ‎     ‎ ‎24.在△ABC中，AB=AC，∠BAC=100°，点D在BC边上，△ABD和△AFD关于直线AD对称，∠FAC的平分线交BC于点G，连接FG．（12分） （1）求∠DFG的度数； （2）设∠BAD=θ， ①当θ为何值时，△DFG为等腰三角形； ②△DFG有可能是直角三角形吗？若有，请求出相应的θ值；若没有，请说明理由． ‎