三年全国各地中考数学真题分类汇编相交线与平行线 41页

2010-2012年三年全国各地中考数学真题分类汇编 相交线与平行线 一.选择题 1．（2012 临沂）如图，AB∥CD，DB⊥BC，∠1=40°，则∠2 的度数是（　　） 　　A．40°　　B．50°　　C．60°　　D．140° 考点：平行线的性质；直角三角形的性质。 解答：解：∵AB∥CD，DB⊥BC，∠1=40°， ∴∠3=∠1=40°， ∵DB⊥BC， ∴∠2=90°﹣∠3=90°﹣40°=50°．故选 B． 2．（2012 张家界）如图，直线 a、b 被直线 c 所截，下列说法正确的是（　　） 　 A． 当∠1=∠2 时，一定有 a∥b B．当 a∥b 时，一定有∠1=∠2 　 C． 当 a∥b 时，一定有∠1+∠2=90° D．当∠1+∠2=180°时，一定有 a∥b 考点：平行线的判定；平行线的性质。 解答：解：A．若∠1=∠2 不符合 a∥b 的条件，故本选项错误； 3．（2012 中考）如图，直线 a∥b，直线 c 与 a，b 相交，∠1=65°，则∠2=（　Ｂ　） A．115°　　　　B．65°　　　　C．35°　　　　D．25° 4．（2012 山西）如图，直线 AB∥CD，AF 交 CD 于点 E，∠CEF=140°，则∠A 等于（　　） 　 A． 35° B． 40° C． 45° D． 50° 考点：平行线的性质。 解答：解：∵∠CEF=140°， ∴∠FED=180°﹣∠CEF=180°﹣140°=40°， ∵直线 AB∥CD， ∴∠A∠FED=40°． 故选 B． 5．（2012 潜江）如图，AB∥CD，∠A=48°，∠C=22°．则∠E 等于（　　） 　A．70° B．26° C．36° D．16° 考点： 平行线的性质；三角形内角和定理。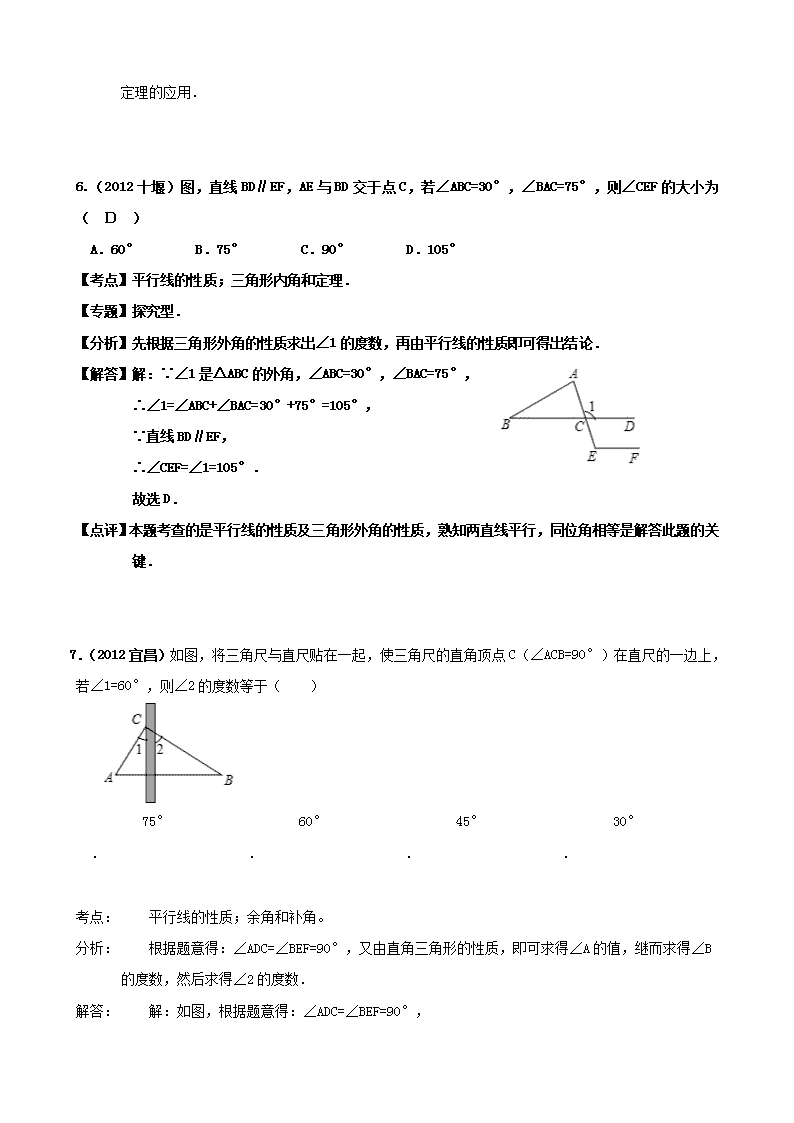 分析： 由 AB∥CD，根据两直线平行，内错角相等，即可求得∠1 的度数，又由三角形外角的性质，即可求 得∠E 的度数． 解答： 解：∵AB∥CD，∠A=48°， ∴∠1=∠A=48°， ∵∠C=22°， ∴∠E=∠1﹣∠C=48°﹣22°=26°． 故选 B． 点评： 此题考查了平行线的性质与三角形外角的性质．此题比较简单，注意掌握两直线平行，内错角相等 定理的应用． 6.（2012 十堰）图，直线 BD∥EF，AE 与 BD 交于点 C，若∠ABC=30°，∠BAC=75°，则∠CEF 的大小为 （　Ｄ　） A．60°　　　　B．75°　　　　C．90°　　　　D．105° 【考点】平行线的性质；三角形内角和定理． 【专题】探究型． 【分析】先根据三角形外角的性质求出∠1 的度数，再由平行线的性质即可得出结论． 【解答】解：∵∠1 是△ABC 的外角，∠ABC=30°，∠BAC=75°， ∴∠1=∠ABC+∠BAC=30°+75°=105°， ∵直线 BD∥EF， ∴∠CEF=∠1=105°． 故选 D． 【点评】本题考查的是平行线的性质及三角形外角的性质，熟知两直线平行，同位角相等是解答此题的关 键． 7．（2012 宜昌）如图，将三角尺与直尺贴在一起，使三角尺的直角顶点 C（∠ACB=90°）在直尺的一边上， 若∠1=60°，则∠2 的度数等于（　　） 　A ． 75° B ． 60° C ． 45° D ． 30° 考点： 平行线的性质；余角和补角。 分析： 根据题意得：∠ADC=∠BEF=90°，又由直角三角形的性质，即可求得∠A 的值，继而求得∠B 的度数，然后求得∠2 的度数． 解答： 解：如图，根据题意得：∠ADC=∠BEF=90°， ∵∠1=60°， ∴∠A=90°﹣∠1=30°， ∵∠ACB=90°， ∴∠B=90°﹣∠A=60°， ∴∠2=90°﹣∠B=30°． 故选 D． 点评： 此题考查了直角三角形的性质．此题难度不大，注意直角三角形中两锐角互余定理的应用是解 此题的关键． 8．（2012 海南）小明同学把一个含有 45 0 角的直角三角板在如图所示的两条平行线 上，测得 ，则 的度数是【 】 A．450 B．550 C．650 D．750 【答案】D。 【考点】平行线的性质，平角定义，对顶角的性质，三角形内角和定理。 【分析】∵ ，∴∠ABn= 。∴∠ABC=600。 又∵∠ACB= ，∠A=450， ∴根据三角形内角和定理，得 =1800－600－450=750。故选 D。 9．(2012•连云港)如图，将三角尺的直角顶点放在直线 a 上，a∥b，∠1＝50°，∠2＝60°，则∠3 的度 数为(　　) 　A．50° B．60° C．70° D．80° 解答： 解：∵△BCD 中，∠1＝50°，∠2＝60°， m n， 0120α∠ = β∠ m n∥ 0120α∠ = β∠ β∠ ∴∠4＝180°－∠1－∠2＝180°－50°－60°＝70°， ∴∠5＝∠4＝70°， ∵a∥b， ∴∠3＝∠5＝70°． 故选 C． 点评： 本题考查的是平行线的性质，解答此类题目时往往用到三角形的内角和是 180°这一 隐藏条件． 10.(2012 重庆)已知：如图，BD 平分∠ABC，点 E 在 BC 上，EF//AB．若∠CEF=100°，则∠ABD 的度数为( ) A.60° B.50° C.40° D.30° 解析：本题由平行很容易想到同位角相等，再由角平分线的性质可得证。 答案：B 点评：由平行线想到同位角相等，内错角相等，同旁内角互补，是解本题的关键。 11.（2012 玉林）如图， ∥ ， 与 ， 都相交，∠1=50°，则∠2= A.40° B.50° C.100° D.130° F E D CB A a b c a b 分析：根据两直线平行，同位角相等，即可得出∠2 的度数． 解：∵a∥b，∴∠1=∠2=50°．故选 B． 点评：此题考查了平行线的性质，关键是掌握平行线的性质：两直线平行，同位角相等，难度一般． 12.（2012•吉林）如图，在 Rt△ABC 中，∠C=90°．D 为边 CA 延长线上的一点，DE‖AB,∠ADE=42°，则 ∠B 的大小为 (A) 42° (B) 45° (C) 48° (D)58° 解析：C ∵DE‖AB,∠ADE=42°∴∠CAB=42° ∵∠C=90°∴∠B=90-42°= 48°。 考查知识：平行线的性质、三角形的内角和 13.（2012 衡阳）如图，直线 a⊥直线 c，直线 b⊥直线 c，若∠1=70°，则∠2=（　） A．70°B．90°C．110°D．80° 解析：首先根据垂直于同一条直线的两直线平行可得a∥b，再根据两直线平行同位角相等可得∠1=∠3．根 据对顶角相等可得∠2=∠3，利用等量代换可得到∠2=∠1=70°． 答案：解：∵直线 a⊥直线 c，直线 b⊥直线 c， ∴a∥b， ∴∠1=∠3， ∵∠3=∠2， ∴∠2=∠1=70°． 故选：A． 点评：此题主要考查了平行线的判定与性质，关键是掌握平行线的判定方法与性质定理． 14.（2012 呼和浩特）如图，已知 a∥b，∠1=65°，则∠2 的度数为 A. 65° B. 125° C. 115° D. 25° 【解析】平行线的性质。法一，由 a∥b，根据两直线平行，同位角相等，即可求得∠3 的度数，又由邻补 角的定义，即可求得∠2 的度数．法二，由对顶角相等，可求得∠4 的度数，再由由 a∥b，根据两直线平 行，同旁内角互补求得∠2 的度数。 法一：∵a∥b，∴∠1=∠3=65°，又∵∠2+∠3=180°，∴∠2=115° 法二：∵∠1=∠4=65°，∵a∥b，∴∠4+∠2=180°，∴∠2=115° a b2 1 【答案】C 【点评】此题考查了平行线的性质．注意两直线平行，同位角相等与数形结合思想的应用． 15.（2012•内江）如图 1， （ ） A. B. C. D. 【解析】：如图 1：连接 AC，则 ， ，故选 B 【考点】：本题考查三角形内角和定理，平行线的性质，以及构造图象添加辅助线。 16.（2012 绥化）如图，AB∥ED，∠ECF=70o，则∠BAF 的度数为（ ） A．130o B．110o C．70o D．20o 【解析】解：∵AB∥ED，∴∠BAC=∠ECF=70o，∴∠BAF=180o-70o=110o．故选 B． 【答案】 B． 【点评】 本题主要考查了平行线性质及邻补角概念，考生不难解决此种类型的题目．难度较小． a b 4 32 1 =∠=∠=∠ 3,1402,651,// 00 则ba 0100 0105 0110 0115 02 3 1 180∠ + ∠ − ∠ = 0 0 0 0 03 180 1 2 180 65 140 105∴∠ = + ∠ − ∠ = + − = 17. （2012 广元）一辆汽车在公路上行驶，两次拐弯后，仍在原来的方向上平行行驶，那么两个拐弯的 角度可能为【 】 A. 先向左转 130°，再向左转 50° B. 先向左转 50°，再向右转 50° C. 先向左转 50°，再向右转 40° D. 先向左转 50°，再向左转 40° 【答案】B。 【考点】平行线的性质。 【分析】根据题意画出图形，然后利用同位角相等，两直线平行与内错角相等，两直线平行，即可判定： 如图： A、∵∠1=130°，∴∠3=50°=∠2。∴a∥b，且方向相反； B、∵∠1=∠2=50°，∴a∥b； C、∵∠1=50°，∠2=40°，∴∠1≠∠2，∴a 不平行于 b； D、∵∠2=40°，∴∠3=140°≠∠1，∴a 不平行于 b。 故选 B。 18.（2012 盐城）一只因损坏而倾斜的椅子，从背后看到的形状如图，其中两组对边的平行关系没有发生 变化，若∠1=750，则∠2 的大小是 A．750　B．1150　　C．650　D． 1050 【解析】本题考查了两条直线平行，同位角，内错角相等，同旁内角互补的性质，掌握平行线的性质是 关键.两组直线分别平行就构成平行四边形，再由平行四边形对角相等，最后利用邻补角解决 1050，故选 D. 【答案】两组直线分别平行就构成平行四边形，所以∠2 的邻补角是 750，所以∠2 的大小是 1050，故选 第 6 题图 D. 【点评】本题考查了平行线的性质，角度的计算，本题充分体现了数形结合的思想，要结合平行线性质 （可以推导角等或互补）熟练进行角间的数量关系的转换． 19．（2012•杭州）如图，在 Rt△ABO 中，斜边 AB=1．若 OC∥BA，∠AOC=36°，则（　　） 　　A．点 B 到 AO 的距离为 sin54°　　B．点 B 到 AO 的距离为 tan36°　　C．点 A 到 OC 的距离为 sin36°sin54°　　D．点 A 到 OC 的距离为 cos36°sin54° 考点：解直角三角形；点到直线的距离；平行线的性质。 分析：根据图形得出 B 到 AO 的距离是指 BO 的长，过 A 作 AD⊥OC 于 D，则 AD 的长是点 A 到 OC 的距离，根 据锐角三角形函数定义得出 BO=ABsin36°，即可判断 A、B；过 A 作 AD⊥OC 于 D，则 AD 的长是点 A 到 OC 的距离，根据锐角三角形函数定义得出 AD=AOsin36°，AO=AB•sin54°，求出 AD，即可判断 C、D． 解答： 解： A、B 到 AO 的距离是指 BO 的长， ∵AB∥OC， ∴∠BAO=∠AOC=36°， ∵在 Rt△BOA 中，∠BOA=90°，AB=1， ∴sin36°= ， ∴BO=ABsin36°=sin36°， 故本选项错误； B、由以上可知，选项错误； C、过 A 作 AD⊥OC 于 D，则 AD 的长是点 A 到 OC 的距离， ∵∠BAO=36°，∠AOB=90°， ∴∠ABO=54°， ∵sin36°= ， ∴AD=AO•sin36°， ∵sin54°= ， ∴AO=AB•sin54°， ∴AD=AB•sin54°•sin36°=sin54°•sin36°，故本选项正确； D、由以上可知，选项错误； 故选 C． 点评：本题考查了对解直角三角形和点到直线的距离的应用，解此题的关键是①找出点 A 到 OC 的距离和 B 到 AO 的距离，②熟练地运用锐角三角形函数的定义求出关系式，题目较好，但是一道比较容易出错 的题目． 20．（2012 泰安）如图，在平行四边形 ABCD 中，过点 C 的直线 CE⊥AB，垂足为 E，若∠EAD=53°，则∠BCE 的度数为（　　） 　　A．53°　　B．37°　　C．47°　　D．123° 考点：平行四边形的性质。 解答：解：∵在平行四边形 ABCD 中，过点 C 的直线 CE⊥AB， ∴∠E=90°， ∵∠EAD=53°， ∴∠EFA=90°﹣53°=37°， ∴∠DFC=37 ∵四边形 ABCD 是平行四边形， ∴AD∥BC， ∴∠BCE=∠DFC=37°． 故选 B． 21.（2012 东营）下图能说明∠1＞∠2 的是( ) 【解析】图 A 中，根据对顶角相等可得∠1=∠2，图 B 中根据两直线平行，同位角相等可得∠1=∠2，图 C 中根据三角形的外角大于不相邻的内角可知∠1＞∠2，图 D 中根据同角的余角相等可得∠1=∠2. 【答案】C. 【点评】主要考查对顶角的性质，平行线的性质，三角形外角的性质，直角三角形的性质，熟记这些性质 是解题的基础。 二.填空题 22.（2012 河北）14、如图 7，AB，CD 相交于点 O，AC⊥ＣＤ与点Ｃ，若∠BOD=38°，则∠A 等于______ °。 【解析】又对顶角性质和直角三角形两锐角互余，可以求出∠A 的度数。 【答案】52 【点评】本题主要考查“对顶角相等”和“直角三角形中两锐角互余”，这两条性质，属于简单题型。 12 ) A. 2 1 ) D. 1 2) ) B. 12) ) C. 23．（2012 义乌市）如图，已知 a∥b，小亮把三角板的直角顶点放在直线 b 上．若∠1=40°，则∠2 的度 数为　50°　． 考点：平行线的性质；余角和补角。 解答：解：∵∠1=40°， ∴∠3=180°﹣∠1﹣45°=180°﹣40°﹣90°=50°， ∵a∥b， ∴∠2=∠3=50°． 故答案为：50°． 24．（2012 长沙）如图，AB∥CD∥EF，那么∠BAC+∠ACE+∠CEF=　360　度． 解答： 解：∵AB∥CD， ∴∠BAC+∠ACD=180°…①， ∵CD∥EF， ∴∠CEF+∠ECD=180°…②， ①+②得， ∠BAC+∠ACD+∠CEF+∠ECD=180°+180°=360°， 即∠BAC+∠ACE+∠CEF=360°． 25．（2012 宜宾）如图，已知∠1=∠2=∠3=59°，则∠4= ． 考点：平行线的判定与性质。 解答： 解：∵∠1=∠3， ∴AB∥CD， ∴∠5+∠4=180°，又∠5=∠2=59°， ∴∠4=180°﹣59°=121°． 故答案为：121° 26.（2012 贵阳）如图，已知∠1=∠2，则图中互相平行的线段是 . 解析： 因为∠1 与∠2 是直线 AD，BC 被 AC 所截形成的内错角，根据“内错角相等，两直线平行”的结论， 得 AD∥BC. 答案： AD∥BC（或 AD 与 BC 平行）. 点评：两直线平行的判定与性质也是中考常考内容，较简单. 27．（2012•宁波）如图，AE∥BD，C 是 BD 上的点，且 AB=BC，∠ACD=110°，则∠EAB=　40　度． A D B C 1 2 考点： 等腰三角形的性质；平行线的性质。 分析： 首先利用∠ACD=110°求得∠ACB 与∠BAC 的度数，然后利用三角形内角和定理求得∠B 的度数，然 后利用平行线的性质求得结论即可． 解答： 解：∵AB=BC， ∴∠ACB=∠BAC ∵∠ACD=110° ∴∠ACB=∠BAC=70° ∴∠B=∠40°， ∵AE∥BD， ∴∠EAB=40°， 故答案为 40°． 点评： 本题考查了等腰三角形的性质及平行线的性质，题目相对比较简单，属于基础题． 28．（2012 成都）如图，将 ABCD 的一边 BC 延长至 E，若∠A=110°，则∠1=________． 考点：平行四边形的性质。 解答：解：∵平行四边形 ABCD 的∠A=110°， ∴∠BCD=∠A=110°， ∴∠1=180°﹣∠BCD=180°﹣110°=70°． 故答案为：70°． 三.解答题  1 A B C D 29．（2012•益阳）如图，已知 AE∥BC，AE 平分∠DAC． 求证：AB=AC． 考点：等腰三角形的判定与性质；平行线的性质；等腰三角形的判定。 专题：证明题。 分析：根据角平分线的定义可得∠1=∠2，再根据两直线平行，同位角相等可得∠1=∠B，两直线平行，内 错角相等可得∠2=∠C，从而得到∠B=∠C，然后根据等角对等边即可得证． 解答：证明：∵AE 平分∠DAC， ∴∠1=∠2， ∵AE∥BC， ∴∠1=∠B，∠2=∠C， ∴∠B=∠C， ∴AB=AC． 点评：本题考查了等腰三角形的判定，平行线的性质，是基础题，熟记性质是解题的关键． 2011 年全国各地中考数学真题分类汇编 第 20 章 相交线与平行线 一、选择题 1. （2011 山东德州 4,3 分）如图，直线 l1∥l2， ∠1=40°，∠2=75°，则∠3 等于 （A）55° （B） 60° （C）65° （D） 70° l1 l2 1 2 3 【答案】C 2. （2011 山东日照，3，3 分）如图，已知直线 ， ， ，那么 的大小 为（ ） （A）70 （B）80 （C）90 （D）100 【答案】B 3. （2011 山东泰安，8 ，3 分）如图 ，l∥m，等腰直角三角形 ABC 的直角顶点 C 在直线 m 上，若 ∠β=200，则∠α 的度数为（ ） A.250 B.300 C.200 D.350 【答案】A 4. （2011 四川南充市，3，3 分） 如图，直线 DE 经过点 A,DE∥BC,,∠B=60°,下列结论成立的是（ ） （A）∠C=60° （B）∠DAB=60° （C）∠EAC=60° （D）∠BAC=60° 　　 【答案】B 5. （2011 山东枣庄，2，3 分）如图，直线 AB∥CD，∠A＝70°，∠C＝40°，则∠E 等于（ ） A．30°　 Ｂ．40° 　C．60°　　 Ｄ．70° AB CD∥ 125C∠ = ° 45A∠ = ° E∠ ED CB A A C B D E 【答案】A 6. （2010 湖北孝感，3，3 分）如图，直线 AB、CD 相交于点 O，OT⊥AB 于 O，CE∥AB 交 CD 于点 C，若∠ECO=30°，则∠DOT=（ ） A.30° B.45° C. 60° D. 120° 【答案】C 7. （2011 河北，2，2 分）如图 1∠1+∠2=（ ） 图 1 A．60° B．90° C．110° D．180° 【答案】B 8. （2011 宁波市，8，3 分）如图所示，AB∥CD，∠E＝37°， ∠C＝20°， ∠EAB 的度数为 A． 57° B． 60° C． 63° D． 123° 【答案】A 9. （2011 浙江衢州，12,4 分）如图，直尺一边 与量角器的零刻度线 平行，若量角器的一条刻度 线 的 读 书 为 70 ° ， 与 交 于 点 , 那 么 度 . 21 AB CD OF OF AB E AEF∠ = 【答案】70 10．（2011 浙江绍兴，3，4 分）如图，已知 的度数是 ( ) A. B. C. D. 【答案】D 11. （2011 浙江义乌，8，3 分）如图，已知 AB∥CD，∠A=60°，∠C =25°，则∠E 等于 A. 60° B. 25° C. 35° D. 45° 【答案】C 12. （2011 四川重庆，4，4 分）如图，AB∥CD，∠C＝80°，∠CAD＝60°，则∠BAD 的度数等于( ) A．60° B．50° C． 45° D． 40° 【答案】D / / , , 34AB CD BC ABE C BED∠ ∠ = ° ∠平分 ，则 17° 34° 56° 68° EC A B D A B C D E 60° 0o 180o0o 180o 170o 170o 160o 160o150o 150o140o 140o 30o 30o 40o 40o 50o 50o 110o 110o 120o 120o 130o 130o90o 90o 100o 100o 60o 60o 70o 70o 80o 80o 20o 20o 10o10o 121110987654320 1 A B F C O D （第 12 题） （第 3 题图） 13. （2011 浙江丽水，5，3 分）如图，有一块含有 45°角的直角三角板的两个顶点放在直尺的对边上.如 果∠1＝20°，那么∠2 的度数是（ ） A．30° B.25° C.20° D.15° 【答案】B 14.（2011 台湾台北，8）图(二)中有四条互相不平行的直线 L1、L2、L3、L4 所截出的七个角。关于这七个 角的度 数关系，下列何者正确？ A． B。 C． D。 【答案】C 15. （2011 台湾全区，7）若△ABC 中，2（∠A＋∠C）＝3∠B，则∠B 的外角度数为何？ A．36 B．72 C．108 D．144 【答案】Ｃ 16. （2011 湖南邵阳，8，3 分）如图（三）所示，已知 O 是直线 AB 上一点，∠1=40°，OD 平分角 BOD， 则∠2 的度数是（） A.20° B.25° C.30° D.70° 【答案】D.提示：∠1+2∠2=180°，∠1=40°，故∠2=70°。 17. （2011 广东株洲，5，3 分）某商品的商标可以抽象为如图所示的三条线段，其中 AB∥CD，∠EAB=45°，则∠FDC 的度数是( ) A． B． C． D． 2 1 742 ∠∠∠ ＋＝ 613 ∠∠∠ ＋＝ °∠∠∠ 180641 ＝＋＋ °∠∠∠ 360532 ＝＋＋ 1 2 A BO C D 30° 45° 60° 75° 【答案】B 18. （2011 山东济宁，6，3 分）如图，AE∥BD，∠1=120°，∠2=40°，则∠C 的度数是 A．10° B．20° C．30° D．40° 【答案】B 19. （2011 山东聊城，4，3 分）如图，已知 a∥b，∠1＝50°，则∠2 的度数是（ ） A．40° B．50° C．120° D．130° 【答案】D 20．（2011 四川宜宾,4,3 分）如图，直线 AB、CD 相交与点 E，DF∥AB．若∠D=70°，则∠CEB 等于（ ） A．70° B．80° C．90° D．110° （第 4 题图） 2 1 E D C B A 第 6 题 【答案】D 21. （ 2011 重庆江津， 5，4 分）下列说法不正确是( ) A.两直线平行,同位角相等; B 两点之间直线最短 C.对顶角相等; D.半圆所对的圆周角是直角· 【答案】B· 22. (2011 重庆綦江，5，4 分)如图，直线 a∥b， AC⊥AB，AC 交直线 b 于点 C，∠1＝65°，则∠2 的度数 是（ ） A. 65° B. 50° C. 35° D. 25° 【答案】：D 23. （2011 湖南怀化，4，3 分）如图 2，已知直线 a∥b,∠1=40°,∠2=60°,则∠3 等于 A.100° B.60° C．40° D.20° 【答案】A 24. （2011 江苏南通，5，3 分）已知：如图 AB∥CD，∠DCE＝80°，则∠BEF 的度数为 A. 120° B. 110° C. 100° D. 80° 【答案】C 25. （2011 山东临沂，3，3 分）如图，已知 AB∥CD，∠1＝70°，则∠3 的度数是（ ） A．60° B．70° C．80° D．110° 【答案】D 26.（2011 湖北黄石，8，3 分）平面上不重合的两点确定一条直线，不同三点最多可确定 3 条直线，若平 面上不同的 n 个点最多可确定 21 条直线，则 n 的值为 A. 5 B. 6 C. 7 D. 8 【答案】B 27. （2011 湖南邵阳，8，3 分）如图（三）所示，已知 O 是直线 AB 上一点，∠1=40°，OD 平分角 BOD， 则∠2 的度数是（） A.20° B.25° C.30° D.70° 【答案】D. 28. （2011 广东茂名，3，3 分）如图，已知 AB∥CD, 则图中与∠1 互补的角有 A．2 个 B．3 个 C．4 个 D．5 个 【答案】A 29. （2011 湖北襄阳，4，3 分）如图 1，CD∥AB，∠1＝120°，∠2＝80°，则∠E 的度数是 A.40° B.60° C.80° D.120° 【答案】A 30. （2011 广东湛江 10,3 分）如图，直线 相交于点 ， ,若 ，则 1 2 A BO C D AB CD、 E //DF AB 100AEC °∠ = D∠ 2 1 E DC BA 图 1 等于 A B C D 【答案】B 31. （2011贵州安顺，3，3分）如图，己知AB∥CD，BE平分∠ABC，∠CDE=150°，则∠C的度数是（ ） A．100° B．110° C．120° D．150° 【答案】C 二、填空题 1. （2011 广东湛江 14,4 分）已知 ，则 的补角的度数为 度． 【答案】150 2. （2011 湖南湘潭市，11，3 分）如图， ∥ ，若∠2＝130°，则∠1＝_______度. 【答案】50° 3. （2011 广东广州市，15，3 分）已知三条不同的直线 a，b，c 在同一平面内，下列四个命题： ①如果 a∥b，a⊥c，那么 b⊥c; ②如果 b∥a，c∥a，那么 b∥c； ③如果 b⊥a，c⊥a，那么 b⊥c；　④如果 b⊥a，c⊥a，那么 b∥c． 其中真命题的是　　　　　．（填写所有真命题的序号） 【答案】①②④ 4. (2011 浙江湖州，12，4).如图，已知 CD 平分∠ACD，DE∥AC，∠1＝30°，则∠2＝ 度． 70° 80° 90° 100° 1 30°∠ = 1∠ a b 2 l 1 a b 第 3 题图 【答案】60 5. （2011 浙江省，11，3 分）已知∠A=40°,则∠A 的补角等于 ． 【答案】140º 6. （2011 浙江温州，13，5 分）如图，a∥b，∠1＝40°，∠2=80°，则∠3= 度． 【答案】120 7. （2011 湖南邵阳，15，3 分）如图（五）所示，AB∥CD，MN 分别交 AB，CD 于点 E，F。已知∠1=35°， 则∠2=________。 【答案】35°。提示：同位角相等。 8. （ 2011 江 苏 泰 州 ， 15 ， 3 分 ） 如 图 ， 直 线 a 、 b 被 直 线 l 所 截 ， a ∥ b ， ∠ 1=70 ° ， 则 ∠ 2= ° ． 【答案】110 9. （2011 四川广安，12，3 分）如图 2 所示，直线 ∥ ．直线 与直线 ， 分别相交于点 、点 ， ，垂足为点 ，若 ，则 = _________ 2 1 a b l a b c a b A B AM b⊥ M 1 58∠ = ° 2∠ 【答案】32° 10．（2011 江苏淮安，12，3 分）如图，直线a、b 被直线 c 所截，a∥b，∠1=70°，则∠2= . 【答案】110° 11. （2011 江苏南通，11，3 分）已知∠α＝20°，则∠α的余角等于 ▲ 度. 【答案】70°. 12. （2011 上海，15，4 分）如图， AM 是△ABC 的中线，设向量 ， ，那么向量 ____________（结果用 、 表示）． 【答案】 13. （2011 四川绵阳 14，4）如图，AB∥CP，交 AB 于 O，AO=PO,若∠C = 50°，则∠A=____度 AB a=  BC b=  AM = a b 1 2a b+  50° O C D P A B M C BA 图 2 M b a c A B 1 2 A B C北 东 （第 10 题） 【答案】25° 14. （2011 安徽芜湖，11,5 分）一个角的补角是 ，这个角是 ． 【答案】 15. （2011 贵州贵阳，11，4 分）如图，ED∥AB，AF 交 ED 于点 C，∠ECF=138°，则∠A =______度． （第 11 题图） 【答案】42 2010年全国各地中考数学真题分类汇编 第 20 章 相交线与平行线 一、选择题 1．（2010 山东济宁） 在一次夏令营活动中，小霞同学从营地 点出发，要到距离 点 的 地去， 先沿北偏东 方向到达 地，然后再沿北偏西 方向走了 到达目的地 ,此时小霞在营地 的 A. 北偏东 方向上 B. 北偏东 方向上 C. 北偏东 方向上 D. 北偏西 方向上 【答案】C 2．2．（2010 山东威海）如图，在△ABC 中，∠C＝90°．若 BD∥AE，∠DBC＝20°，则∠CAE 的度数 是 A．40° 36 35′ 143 25′ A A 1000 m C 70° B 20° 500 m C A 20° 30° 40° 30° A B C D E A C B D E 第 2 题图 B．60° C．70° D．80° 【答案】C 3．（2010 山东聊城） 如图，l∥m，∠1＝115º，∠2＝ 95º，则∠3＝（ ） A．120º　 B．130º　　 C．140º 　　D．150º 【答案】D 4．（2010 山东省德州）如图，直线 AB∥CD，∠A＝70°，∠C＝40°，则∠E 等于 （Ａ）30°　 （Ｂ）40°　 （C）60°　 （Ｄ）70° 【答案】A 5．（2010 四川成都）如图，已知 ， ，则 的度数为（ ） （A） （B） （C） （D） 【答案】B 6．（2010 广东中山）如图，已知∠1= ，如果 CD∥BE，那么∠B 的度数为 （ ） //AB ED 65ECF∠ =  BAC∠ 115 65 60 25 070 A B C D E A B C DE F A． B． C． D． 【答案】C 7．（2010 湖南郴州）下列图形中，由 ，能得到 的是 【答案】 B 8．（2010 四川内江）将一副三角板如图放置，使点 A 在 DE 上，BC∥DE，则∠AFC 的度数为 A．45°　　　　　B．50°　　　　　C．60°　　　　D．75° 【答案】D 9．（2010 广东东莞）如图，已知∠1＝70°如果 CD∥BE，那么∠B 的度数为（ ） A．70° B．100° C．110° D．120° 【答案】C 10．（2010 湖北襄樊）如图 1，已知直线AB//CD，BE 平分∠ABC，交 CD 于 D，∠CDE=150°，则∠C 的度数 070 0100 0110 0120 AB CD 1 2∠ = ∠ 第 3 题图 B C E D A 1 ( 为（ ） A．150° B．130° C．120° D．100° 图 1． 【答案】C 11．（2010 广东汕头）如图，已知∠1 ＝ 70º，如果 CD∥BE，那么∠B 的度数为（　　） A．70º　 B．100º 　C．110º D．120º 【答案】C 12．（2010 甘肃）如图， ， 于 交 于 ，已知 ，则 （ ） A．30° B．20° C．25° D．35° 【答案】A 13．（2010 广西玉林、防城港）如图 1，直线 a∥b，C 与 a、b 均相交，则 ＝　　　　　（　　　　　） A．60 B．100 C．120 D．150 【答案】C A B CD E AB CD∥ EF AB⊥ E EF， CD F 1 60∠ = ° 2∠ = β C D BA E F1 2 图 4 1 b a 2 A B C E F P Q M N 5 题图 14．（2010 山东荷泽） 如图，直线 PQ∥MN，C 是 MN 上一点，CE 交 PQ 于 A，CF 交 PQ 于 B，且∠ECF＝90 °，如果∠FBQ＝50°，则∠ECM 的度数为 A．60° B．50° C．40° D．30° 【答案】C 15．（2010 宁夏回族自治区）如图，BC⊥AE，垂足为 C，过 C 作 CD∥AB．若∠ECD=48°则∠B= ． 【答案】 16．（2010 新疆维吾尔自治区新疆建设兵团）如图，小明课间把老师的三角板的直角顶点放在黑板的两条 平行线 a、b 上，已知∠1=55°，则∠2 的度数为（ ） A. 45° B. 35° C. 55° D.125° 【答案】B 17．（2010 广西梧州）如右图 4，a∥b，如果∠1=50°，则∠2 的度数是 A．130° B．50° C．100° D．120° 【答案】A 18．（2010 年山西）如图，直线 分别与 a、b 相交于点 A、B，已知 的度数为 （ ） E DC BA 042 cba 直线,// 2,351 ∠=∠ 则 A．165° B．155° C．145° D．135° 【答案】C 19．（2010 云南昭通）如图 2，AB∥CD，EF⊥AB 于点 E，EF 交 CD 于 F，已知∠2=30°，则∠1 是（ ） A．20° B．60° C．30° D．45° 【答案】B 20．（2010 贵州遵义）如图，梯子的各条横档互相平行，若∠1=80 ，则∠2 的度数是 A．80° B．100° C．110° D．120 ° 【答案】B 21．（2010 广西柳州）三条直线 a、b、c，若 a∥c，b∥c，则 a 与 b 的位置关系是 A．a⊥b B．a∥b C．a⊥b 或 a∥b D．无法确定 【答案】B 22．（2010 天门、潜江、仙桃）对于图中标记的各角，下列条件能够推理得到 a∥b 的是( ) A.∠1=∠2 B.∠2=∠4 C.∠3=∠4 D.∠1+∠4=180° 1 F 图 2 2 E DC BA 第8题 54 3 2 1 l b a b E D B A C 【答案】D 23．（2010 广东肇庆）如图 1，AB∥CD，∠A=50°，∠C=∠E，则∠C 等于（ ） A．20° 　　　 B．25° C．30° 　　D．40° 【答案】Ｂ 24．（2010 广西百色）如图，已知 ∥b，分别与 、 相交，下列结论中错误的是（ ） A．∠1=∠3 B. ∠2=∠3 C. ∠1=∠4 D. ∠2=∠5 【答案】D 25．（2010 浙江宁波）如图，直线 AB 与直线 CD 相交于点 O，E 是∠AOD 内一点，已知 OE⊥AB，∠ BOD= ， 则∠COE 的度数是 (A)125° (B)135° (C)145° (D)155° a a b 45 O l2 l1 β α 第 3 题 O E D C BA (第 8 题) 【答案】B 26．（2010 福建福州）下面四个图形中，能判断∠1＞∠2 的是( ) A． B． C． D． 【答案】D 27．（2010 山东滨州） 如图,已知 AB∥CD,BE 平分∠ABC,且 CD 于 D 点, ∠CDE=150°,则∠C 为( ) A.120° B.150° C.135° D.110° 【答案】A 28．（2010 湖南郴州）如图，直线 l1 与 l2 相交于点 O， ，若 ，则 等于 A． B． C． D． 【答案】 B 29．（2010 山东泰安）如图 l1∥l2,l3⊥l4,∠1=42°,那么∠2 的度数为( ) 1OM l⊥ 44α∠ = ° β∠ 56° 46° 45° 44° Ａ．48° Ｂ．42° Ｃ．38° Ｄ．21° 【答案】A 30．（2010 陕西西安）如图，点 O 在直线 AB 上，且 OC⊥OD，若∠COA=36°，则∠DOB 的大小为 A．36° B．54° C．64° D．72° 【答案】B 二、填空题 1．（2010 山东日照）如图，C 岛在 A 岛的北偏东 50o 方向，C 岛在 B 岛的北偏西 40o 方向，则从 C 岛看 A， B 两岛的视角∠ACB 等于 ． 【答案】90o 2．（2010 山东烟台）将两张矩形纸片如图所示摆放，使其中一张矩形纸片的一个顶点恰好落在另一张矩形 纸片的一条边上，则∠1+∠2=_____________。 【答案】90° 3．（2010 浙江杭州）如图, 已知∠1 =∠2 =∠3 = 62°，则 . 4∠ = (第 13 题) C A ED B 【答案】118° 4．（2010 山东济南）如图，直线 ∥ ，直线 与 、 相交，∠1 ＝70°，则∠2 ＝ ． 【答案】70° 5．（2010 浙江衢州）如图，直线 DE 交∠ABC 的边 BA 于点 D，若 DE∥BC，∠B=70°， 则∠ADE 的度数是　　　　　　． 【答案】70° 6．（2010 湖南邵阳）如图（五），AB∥CD，直线 MN 分别与 AB、CD相交于点 E、F，若 MEB＝65°，则 CFN ＝_______． 【答案】65° 7．（2010 湖南衡阳）如图所示，AB∥CD，∠ABE＝66°，∠D＝54°，则∠E 的度数为_______________． a b c a b ∠ ∠ F E N M A C D B B F G H A D E C 1 图 4 D B C F EA 图 1 2 1 【答案】12° 8．（2010 湖南常德）如图 1，已知直线AB//CD，直线 EF 与直线 AB、CD 分别交于点 E、F，且有∠1=70°， 则∠2= . 【答案】 9．（2010 湖南怀化）如图 4，已知直线 ∥b，∠1=40°，则∠2= ． 【答案】 10．（2010 福建三明）如图，已知∠C=100°，若增加一个条件，使得 AB//CD， 试写出符合要求的一个条件： 。 【答案】等，答案不唯一； 11．（2010 四川绵阳）如图，AB∥CD，∠A = 60°，∠C = 25°，C、H 分别为 CF、CE 的中点， 则∠1 = ． 【答案】145° 110° a 40 D CB A (图 4) 2 1 BA C D E F B 11 题图 12．（2010 湖南湘潭）如图，已知 AB∥CD， ，则 o． 【答案】100 13．（2010 贵州贵阳）如图 4，河岸 AD、BC 互相平行，桥 AB 垂直于两岸， 从 C 处看桥的两端 A、B，夹角∠BCA＝60,测得 BC＝7m， 则桥长 AB＝ ▲ m（结果精确到 1m） 【答案】12 14．（2010 广西桂林）如图，直线 AB、CD 被直线 EF 所截， 则∠3 的同旁内角是（ ）． A．∠1 B．∠2 C．∠4 D．∠5 【答案】B 15．（2010 湖北十堰）如图，直线 l1∥l2 被直线 l3 所截，∠1=∠2=35°，∠P=90°，则∠3= . o1 80∠ = =∠2 1 2 3 4 5A B C D E F (第 3 题图) 2 1 l1 l2 l3 3 1 2 P （第 13 题） 【答案】55°． 16．（2010 广西南宁）如图 5 所示，直线 、 被 、 所截，且 ， 则 【答案】70 17．（2010 广东茂名）如图，梯子的各条横档互相平行，若∠1=70o，则∠2 的度数是 A．80o B．110o C．120o D．140o 【答案】B 18．（2010 辽宁大连）如图 3，AB//CD， ，FG 平分 EFD，则 19．（2010 年福建省泉州） 如图，已知：直线 ∥ ， ，则 . 【答案】65° a b c d °=∠⊥⊥ 701,, bcac =∠2 1 60∠ = ° ∠ 2∠ = AB CD °=∠ 651 =∠2 E 1 2 B A DC F G 图 a O 图 b 20．（2010 贵州铜仁）如图，请填写一个你认为恰当的条件_______，使 AB∥CD． 【答案】此题答案不唯一，填写的条件可以是∠CDA＝∠DAB 或∠PCD＝∠BAC 或∠BAC＋∠ACD＝180°等 21．（2010 云南曲靖）如图，AB//CD，AC⊥BC，垂足为 C，若∠A=400，则∠BCD= 度。 【答案】50 【答案】30 三、解答题 1．（2010 云南玉溪）平面内的两条直线有相交和平行两种位置关系. （1）如图 a，若 AB∥CD，点 P 在 AB、CD 外部，则有∠B=∠BOD，又因∠BOD 是 △POD 的外角，故∠BOD=∠BPD +∠D，得∠BPD=∠B-∠D．将点 P 移到 AB、CD 内部，如图 b，以上 结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D 之间有何数量关系？请证明你 的结论； （2）在图 b 中，将直线 AB 绕点 B 逆时针方向旋转一定角度交直线 CD 于点 Q，如图 c，则∠BPD﹑∠B﹑∠ D﹑∠BQD 之间有何数量关系？（不需证明）； （3）根据（2）的结论求图 d 中∠A+∠B+∠C+∠D+∠E+∠F 的度数． 图 3 图 c 图 d 【答案】解：（1）不成立，结论是∠BPD=∠B+∠D. 延长 BP 交 CD 于点 E, ∵AB∥CD. ∴∠B=∠BED. 又∠BPD=∠BED+∠D， ∴∠BPD=∠B+∠D. …………4 分 （2）结论： ∠BPD=∠BQD+∠B+∠D. …………7 分 （3）由（2）的结论得：∠AGB=∠A+∠B+∠E. 又∵∠AGB=∠CGF. ∠CGF+∠C+∠D+∠F=360° ∴∠A+∠B+∠C+∠D∠E+∠F=360°. …………11 分