中考数学最短路问题 3页

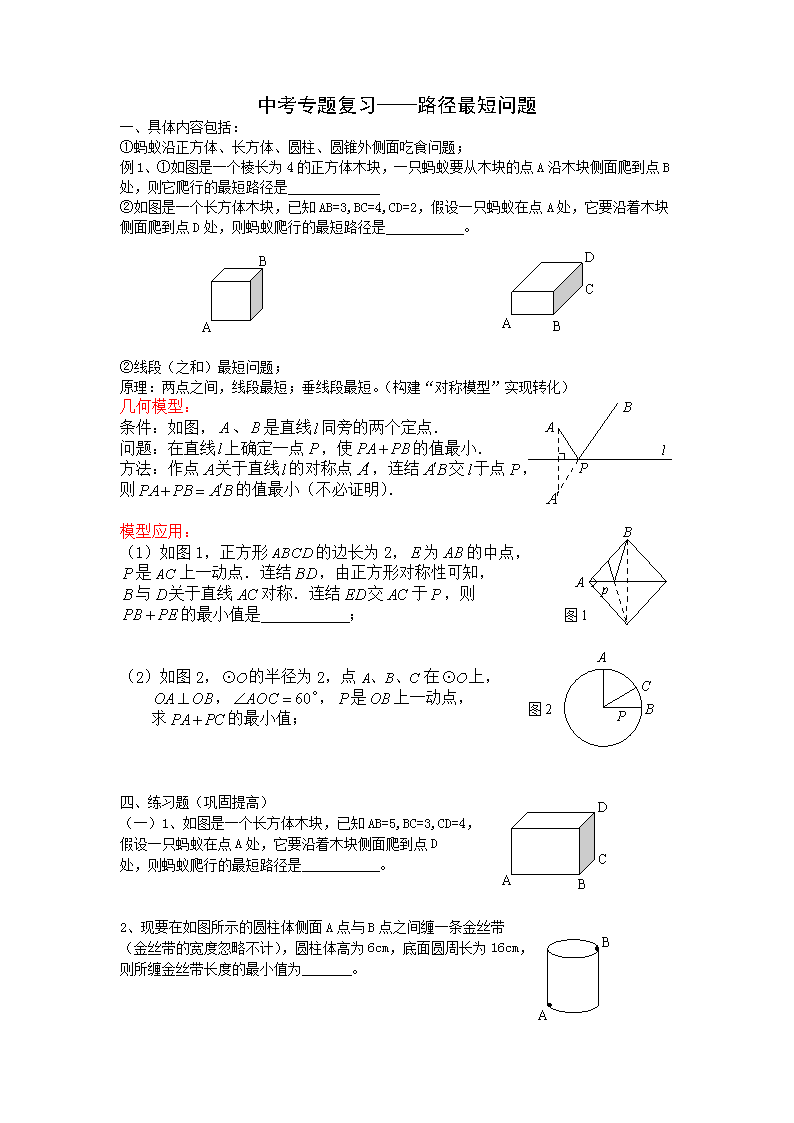
中考专题复习——路径最短问题 一、具体内容包括：‎ ‎①蚂蚁沿正方体、长方体、圆柱、圆锥外侧面吃食问题；‎ 例1、①如图是一个棱长为4的正方体木块，一只蚂蚁要从木块的点A沿木块侧面爬到点B处，则它爬行的最短路径是 ‎ ‎②如图是一个长方体木块，已知AB=3,BC=4,CD=2，假设一只蚂蚁在点A处，它要沿着木块侧面爬到点D处，则蚂蚁爬行的最短路径是 。‎ A B C D A B ‎②线段（之和）最短问题；‎ 原理：两点之间，线段最短；垂线段最短。（构建“对称模型”实现转化）‎ A B ‎′‎ P l 几何模型：‎ 条件：如图，、是直线同旁的两个定点．‎ 问题：在直线上确定一点，使的值最小．‎ 方法：作点关于直线的对称点，连结交于点，‎ 则的值最小（不必证明）．‎ A B E c p D 图1‎ 模型应用：‎ ‎（1）如图1，正方形的边长为2，为的中点，‎ 是上一动点．连结，由正方形对称性可知，‎ 与关于直线对称．连结交于，则 的最小值是___________；‎ O A B C 图2‎ P ‎（2）如图2，的半径为2，点在上，‎ ‎，，是上一动点，‎ 求的最小值；‎ A B C D 四、练习题（巩固提高）‎ ‎（一）1、如图是一个长方体木块，已知AB=5,BC=3,CD=4，‎ 假设一只蚂蚁在点A处，它要沿着木块侧面爬到点D 处，则蚂蚁爬行的最短路径是 。‎ A B ‎2、现要在如图所示的圆柱体侧面A点与B点之间缠一条金丝带 ‎（金丝带的宽度忽略不计），圆柱体高为‎6cm，底面圆周长为‎16cm，‎ 则所缠金丝带长度的最小值为 。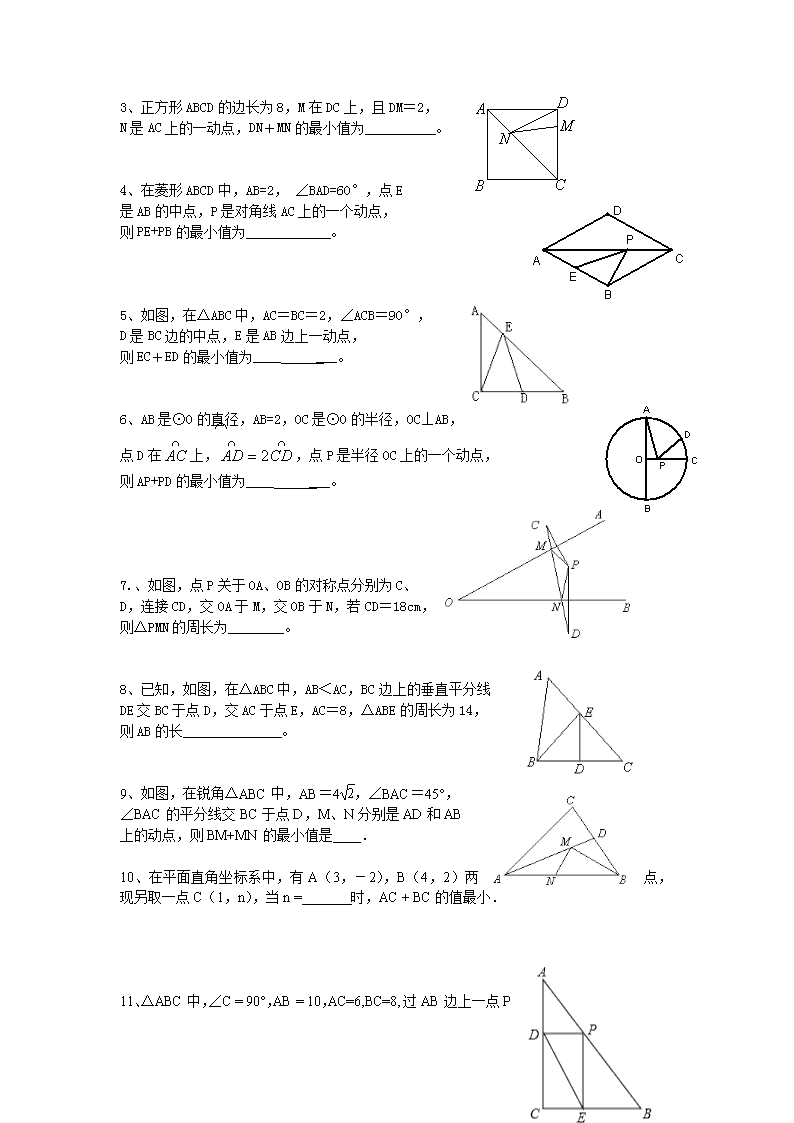‎ ‎3、正方形ABCD的边长为8，M在DC上，且DM＝2，‎ N是AC上的一动点，DN＋MN的最小值为 。‎ ‎ ‎ ‎4、在菱形ABCD中，AB=2， ∠BAD=60°，点E 是AB的中点，P是对角线AC上的一个动点，‎ 则PE+PB的最小值为 。‎ ‎5、如图，在△ABC中，AC＝BC＝2，∠ACB＝90°，‎ D是BC边的中点，E是AB边上一动点，‎ 则EC＋ED的最小值为____ ___。‎ ‎⌒‎ ‎6、AB是⊙O的直径，AB=2，OC是⊙O的半径，OC⊥AB，‎ 点D在上，，点P是半径OC上的一个动点，‎ 则AP+PD的最小值为____ ___。‎ ‎7.、如图，点P关于OA、OB的对称点分别为C、‎ D，连接CD，交OA于M，交OB于N，若CD＝‎18cm，‎ 则△PMN的周长为________。‎ ‎8、已知，如图，在△ABC中，AB＜AC，BC边上的垂直平分线 DE交BC于点D，交AC于点E，AC＝8，△ABE的周长为14，‎ 则AB的长 。‎ ‎9、如图，在锐角△ABC中，AB＝4，∠BAC＝45°，‎ ‎∠BAC的平分线交BC于点D，M、N分别是AD和AB 上的动点，则BM+MN的最小值是____．‎ ‎10、在平面直角坐标系中，有A（3，－2），B（4，2）两点，‎ 现另取一点C（1，n），当n = 时，AC + BC的值最小．‎ ‎ ‎ ‎11、△ABC中，∠C = 90°，AB = 10，AC=6,BC=8,过AB边上一点P 作PE⊥AC于E，PF⊥BC于 F，E、F是垂足，则EF的最小值等于 ．‎ ‎12、一次函数y=kx+b的图象与x、y轴分别交于点 A（2，0），B（0，4）．‎ ‎（1）求该函数的解析式；‎ ‎（2）O为坐标原点，设OA、AB的中点分别为C、D，‎ P为OB上一动点，求PC＋PD的最小值，并求取得最小值时P点坐标．‎ ‎17.已知：抛物线的对称轴为与轴交于两点，与轴交于点其中、（1）求这条抛物线的函数表达式．‎ ‎（2）已知在对称轴上存在一点P，使得的周长最小．请求出点P的坐标．‎ ‎（3）若点是线段上的一个动点（不与点O、点C重合）．过点D作交轴于点连接、．设的长为，的面积为．求与之间的函数关系式．试说明是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．‎ A C x y B O A C x y B O