中考数学总复习几何初步及三角形 12页

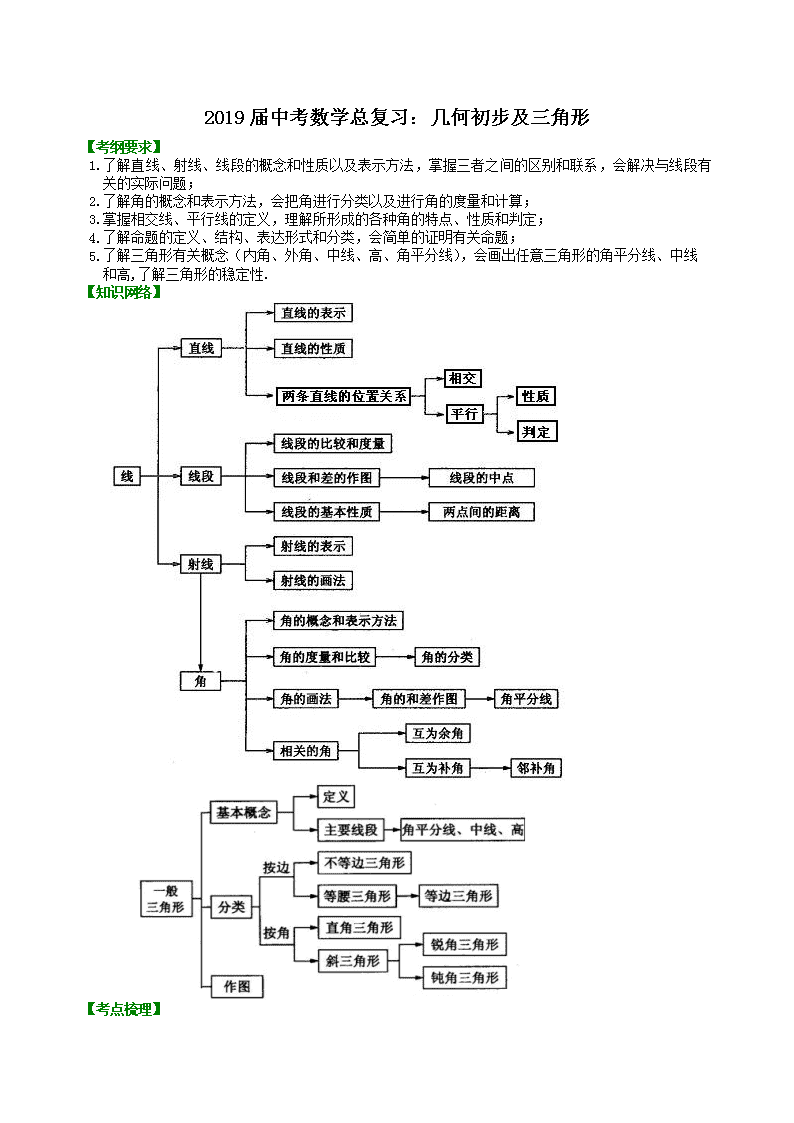
‎2019届中考数学总复习：几何初步及三角形 ‎【考纲要求】‎ ‎1.了解直线、射线、线段的概念和性质以及表示方法，掌握三者之间的区别和联系，会解决与线段有关的实际问题；‎ ‎2.了解角的概念和表示方法，会把角进行分类以及进行角的度量和计算；‎ ‎3.掌握相交线、平行线的定义，理解所形成的各种角的特点、性质和判定；‎ ‎4.了解命题的定义、结构、表达形式和分类，会简单的证明有关命题； 5.了解三角形有关概念（内角、外角、中线、高、角平分线），会画出任意三角形的角平分线、中线 和高,了解三角形的稳定性.　　　 　　　‎ ‎【知识网络】‎ ‎【考点梳理】‎ 考点一、直线、射线和线段 1．直线 　　代数中学习的数轴和一张纸对折后的折痕等都是直线，直线可以向两方无限延伸.(直线的概念是一个描述性的定义，便于理解直线的意义). 要点诠释：‎ ‎1）．直线的两种表示方法： 　　(1)用表示直线上的任意两点的大写字母来表示这条直线，如直线AB，其中A、B是表示直线上两点的字母； 　　(2)用一个小写字母表示直线，如直线a. 2)．直线和点的两种位置关系 　　(1)点在直线上(或说直线经过某点)； 　　(2)点在直线外(或说直线不经过某点). 3).直线的性质： 　 过两点有且只有一条直线(即两点确定一条直线).‎ ‎2．射线 　　直线上一点和它一旁的部分叫做射线.射线只向一方无限延伸. 要点诠释：‎ ‎(1)用表示射线的端点和射线上任意一点的大写字母来表示这条射线，如射线OA，其中O是端点，A是射线上一点； 　　(2)用一个小写字母表示射线，如射线a. 3.线段 　　直线上两点和它们之间的部分叫做线段，两个点叫做线段的端点.‎ 要点诠释： 1)．线段的表示方法： 　　(1)用表示两个端点的大写字母表示，如线段AB，A、B是表示端点的字母； 　　(2)用一个小写字母表示，如线段a. 2)．线段的性质： 　　所有连接两点的线中，线段最短(即两点之间，线段最短). 3)．线段的中点： 　　线段上一点把线段分成相等的两条线段，这个点叫做线段的中点. 4)．两点的距离： 　　连接两点间的线段的长度，叫做两点的距离. 考点二、角 1．角的概念： 　　(1)定义一：有公共端点的两条射线组成的图形叫做角，这个公共端点叫做角的顶点，两条射线分别叫做角的边. 　　(2)定义二：一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角.射线旋转时经过的平面部分是角的内部，射线的端点是角的顶点，射线旋转的初始位置和终止位置分别是角的两条边. 要点诠释：‎ ‎1）．角的表示方法： 　　(1)用三个大写字母来表示，注意将顶点字母写在中间，如∠AOB； 　　(2)用一个大写字母来表示，注意顶点处只有一个角用此法，如∠A； 　　(3)用一个数字或希腊字母来表示，如∠1，∠. 2）．角的分类： 　　(1)按大小分类： 　 　　锐角----小于直角的角(0°＜＜90°); 　 　　直角----平角的一半或90°的角(=90°); 　 　　钝角----大于直角而小于平角的角(90°＜＜180°); 　　(2)平角：一条射线绕着端点旋转，当终止位置与起始位置成一条直线时，所成的角叫做平角，‎ 平角等于180°‎ ‎. 　　(3)周角：一条射线绕着端点旋转，当终止位置又回到起始位置时，所成的角叫做周角，周角等于 　 　　360°. 　　(4)互为余角：如果两个角的和是一个直角(90°)，那么这两个角叫做互为余角. 　　(5)互为补角：如果两个角的和是一个平角(180°)，那么这两个角叫做互为补角. 3）．角的度量： 　　(1)度量单位：度、分、秒； 　　(2)角度单位间的换算：1°=60′，1′=60″(即：1度=60分，1分=60秒)； 　　(3)1平角=180°，1周角=360°，1直角=90°. 4）．角的性质： 　　同角或等角的余角相等，同角或等角的补角相等. 2．角的平分线： 　　如果一条射线把一个角分成两个相等的角，那么这条射线叫做这个角的平分线. 考点三、相交线 1．对顶角 　　(1)定义：如果两个角有一个公共顶点， 而且一个角的两边分别是另一角两边的反向延长线，那么这两个角叫对顶角. 　　(2)性质：对顶角相等. 2．邻补角 　　(1)定义：有一条公共边，而且另一边互为反向延长线的两个角叫做邻补角. 　　(2)性质：邻补角互补. 3．垂线 （1）定义：当两条直线相交所得的四个角中，有一个角是直角时，就说这两条直线是互相垂直的，它们的交点叫做垂足.垂直用符号“⊥”来表示. 要点诠释： 　 ①过一点有且只有一条直线与已知直线垂直.‎ ‎②连接直线外一点与直线上各点的所有线段中，垂线段最短.简单说成：垂线段最短. (2)点到直线的距离定义：直线外一点到这条直线的垂线段的长度，叫做点到直线的距离. 4．同位角、内错角、同旁内角 　　(1)基本概念：两条直线(如a、b)被第三条直线(如c)所截，构成八个角，简称三线八角，如图所示： ∠1和∠8、∠2和∠7、∠3和∠6、∠4和∠5是同位角；∠1和∠6、∠2和∠5是内错角；∠1和∠5、∠2和∠6是同旁内角. 　 (2)特点：同位角、内错角、同旁内角都是由三条直线相交构成的两个角.两个角的一条边在同一直线(截线)上，另一条边分别在两条直线(被截线)上. ‎ ‎ 考点四、平行线 1．平行线定义： 　　在同一平面内，不相交的两条直线叫做平行线.平行用符号“∥”来表示，.如直线a与b平行，记作a∥b.在几何证明中，“∥”的左、右两边也可能是射线或线段. 2．平行公理及推论： ‎ ‎　　(1)经过直线外一点，有且只有一条直线与这条直线平行. 　　(2)平行公理推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行.即： 　 　　如果b∥a，c∥a，那么b∥c. 3．性质： 　　(1)平行线永远不相交； 　　(2)两直线平行，同位角相等； 　　(3)两直线平行，内错角相等； 　　(4)两直线平行，同旁内角互补； 　　(5)如果两条平行线中的一条垂直于某直线，那么另一条也垂直于这条直线，可用符号表示为： 　 　　若b∥c，b⊥a，则c⊥a. 4．判定方法： 　　(1)定义； 　　(2)平行公理的的推论； 　　(3)同位角相等，两直线平行； 　　(4)内错角相等，两直线平行； 　　(5)同旁内角互补，两直线平行； 　　(6)垂直于同一条直线的两条直线平行. 考点五、命题、定理、证明 1．命题： 　　(1)定义：判断一件事情的语句叫命题. 　　(2)命题的结构：题设+结论=命题； 　　(3)命题的表达形式：如果……那么……；若……则……； 　　(4)命题的分类：真命题和假命题； 　　(5)逆命题：原命题的题设是逆命题的结论，原命题的结论是逆命题的题设. 2．公理、定理： 　　(1)公理：人们在长期实践中总结出来的能作为判断其他命题真假依据的真命题叫做公理. 　　(2)定理：经过推理证实的真命题叫做定理. 3．证明： 　　用推理的方法证实命题正确性的过程叫做证明. 考点六、三角形的概念及其性质 1．三角形的概念 　　由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形. 2．三角形的分类 　　(1)按边分类： 　　　 　　(2)按角分类： 　　　 3．三角形的内角和外角 　　(1)三角形的内角和等于180°. 　　(2)三角形的任意一个外角等于和它不相邻的两个内角之和；三角形的一个外角大于任何一个和它不相邻的内角. 4．三角形三边之间的关系 　　三角形任意两边之和大于第三边，任意两边之差小于第三边. 5．三角形内角与对边对应关系 　　在同一个三角形内，大边对大角，大角对大边；在同一三角形中，等边对等角，等角对等边. 6．三角形具有稳定性.‎ ‎7. 三角形中的四条特殊的线段是：高线、角平分线、中线、中位线. 要点诠释：‎ 三角形的中位线：连结三角形两边中点的线段是三角形的中位线. 中位线定理：三角形的中位线平行于第三边且等于第三边的一半.‎ ‎【典型例题】‎ 类型一、直线、射线及线段 ‎1．数轴上有两点A、B分别表示实数a、b，则线段AB的长度是( ) 　　A.a-b　　　 B.a+b 　　　C.│a-b│　　　 D.│a+b│‎ ‎【思路点拨】根据数轴上两点之间的距离公式即可解决问题．‎ ‎【答案】C.‎ ‎【解析】本类题目注意线段长度是非负数，若有字母注意使用绝对值.根据题意，画图.‎ 数轴上两点间的距离公式为：│a-b│或│b-a│.‎ ‎【总结升华】解决本例类型的题目应结合图形，即数形结合，这样做起来简捷.‎ ‎2．有一段火车路线，含这段铁路的首尾两站在内共有5个车站(如图)，图中共有几条线段？在这段线路上往返行车，需印制几种车票(每种车票要印出上车站与下车站)？ ‎ ‎【思路点拨】先求得单程的车票数，再求出往返的车票数即可．‎ ‎【答案与解析】线段有10条；车票需要2×10=20种.‎ ‎【总结升华】在直线上确定线段的条数公式为: (其中n为直线上点的个数).在求从一个顶点引出的n条射线所形成的小于平角的角的个数也可用此公式.‎ 举一反三：‎ ‎【变式】如图，点A、B、C在直线上，则图中共有______条线段. 　　　　　　　　　　　　　　　‎ ‎【答案】3.‎ 类型二、角 ‎3．如图，已知∠COE=∠BOD=∠AOC=90°，则图中互余的角有______对，互补的角有______对. 　　　　　　　　　　　　 ‎ ‎【思路点拨】先要确定等角，再根据角的性质进行判断.‎ ‎【答案与解析】‎ 互余的角有：∠COD和∠DOE、∠COD和∠BOC、∠AOB和∠DOE、∠AOB和∠BOC，共4对；‎ 互补的角有：∠EOD和∠AOD、∠BOC和∠AOD、∠AOB和∠BOE、∠COD和∠BOE、∠AOC和 ‎∠COE、∠AOC和∠BOD、∠COE和∠BOD，共7对.‎ ‎【总结升华】在本题目中，当图中的角比较多时，就将图形的角进行归类，找出每种相等的角，按照同角或等角的余角相等，同角或等角的补角相等的性质解决问题，注意要不重不漏.‎ 举一反三：‎ ‎【变式】【高清课堂：几何初步及三角形 专题一 2】‎ ‎【答案】70°.‎ 类型三、相交线与平行线 ‎4．（2015春•南京校级月考）如图，AB∥CD，则∠α、∠β、∠γ之间的等量关系为　　．‎ ‎【思路点拨】通过观察图形，可作出一条辅助线即平行线，从而把问题化难为易.‎ ‎【答案】∠α+∠β﹣∠γ=180°.‎ ‎【解析】解：如图，过点E作EF∥AB，‎ ‎∴∠1+∠γ=∠β，‎ ‎∵AB∥CD，‎ ‎∴EF∥CD，‎ ‎∴∠1+∠α=180°，‎ ‎∴∠α﹣∠γ=180°﹣∠β，‎ ‎∴∠α+∠β﹣∠γ=180°．‎ 故答案为：∠α+∠β﹣∠γ=180°．‎ ‎【总结升华】本题考点：平行线的性质.‎ 举一反三：‎ ‎【变式】（1）两平行直线被第三条直线所截，同位角的平分线( ) 　　A.互相重合 　　　B.互相平行 　　　C.互相垂直 　　　D.相交 ‎【答案】B.‎ 类型四、三角形 ‎5．（2014•怀化模拟）三角形三边长分别是6，2a﹣2，8，则a的取值范围是（　　）‎ A．1＜a＜2 B．＜a＜2 C．2＜a＜8 D．1＜a＜4‎ ‎【思路点拨】本题考查了三角形的三边关系．此类求三角形第三边的范围的题，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．‎ ‎【答案】C. ‎ ‎【解析】解：由于在三角形中任意两边之和大于第三边，‎ ‎∴2a﹣2＜6+8，即a＜8，‎ 任意两边之差小于第三边，‎ ‎∴2a﹣2＞8﹣6，即a＞2，‎ ‎∴2＜a＜8，‎ 故选：C．‎ ‎【总结升华】涉及到三角形三边关系时，尽可能简化运算，注意运算的准确性.‎ 举一反三：‎ ‎【变式】已知a，b，c为△ABC的三条边，化简得_________.‎ ‎【答案】∵a，b，c为△ABC的三条边 ∴a-b-c＜0， b-a-c＜0 　　　　　∴=(b+c-a)+(a+c-b)=2c.‎ ‎6. 下列命题：(1)等边三角形也是等腰三角形；(2)三角形的外角等于两个内角的和；(3)三角形中最大的内角不能小于60°；(4)锐角三角形中，任意两内角之和必大于90°，其中错误的个数是( ) 　　A.0 个　　　 B.1个　　　 C.2个　　　 D.3个 ‎【思路点拨】认真阅读各小题提供的已知条件，依据三角形的分类方法，然后根据三角形内角和为 ‎180°进行分析解答．‎ ‎【答案】B.‎ ‎【解析】(2)中应强调三角形的外角等于不相邻的两个内角的和；三角形中最大的内角若小于60°，则三个角的和就小于180°，不符合三角形内角和定理，故(3)正确；(4)三角形中，任意两内角之和若不大于90°，则另一个内角就大于或等于90°，就不能是锐角三角形.所以只有(2)错，故选B.‎ ‎【总结升华】本题的解题关键是要理解定义，掌握每种三角形中角的度数的确定.‎ 举一反三：‎ ‎【变式】【高清课堂：几何初步及三角形 专题二 3】‎ ‎【答案】15°.‎ ‎【巩固练习】‎ 一、选择题 ‎1．如图，△ABC中，∠C=90°，AC=3，点P是边BC上的动点，则AP长不可能是( ). 　　　　　　 A．2.5 　　　B．3 　　　C．4 　　　D．5 ‎ ‎2．如图所示，图中线段和射线的条数为( ).‎ A.三条，四条　　　 B.二条，六条 　　　C.三条，六条 　　　D.四条，四条 　　　　　　　　‎ ‎3．下列四个图中，能用∠1、∠AOB、∠O三种方法表示同一个的是( ). 　　‎ ‎4．一个三角形的三个内角中( ). A.至少有一个钝角　　　B.至少有一个直角　 C.至多有一个锐角　　 D.至少有两个锐角 ‎5．（2014秋•上蔡县校级期末）如果三角形的三边长分别为a、a﹣1、a+1，则a的取值范围是（　　）‎ A．a＞0 B．a＞2 C．a＜2 D．0＜a＜2‎ ‎6. 如图，某人不小心把一块三角形的玻璃打碎成三块，现在要到玻璃店去配一块完全一样的玻璃，那么正确的方法是( ). 　　　　　　　　　 A.带①去　　　 B.带②去　　　 C.带③去　　　 D.带①和②去 二、填空题 ‎7．（2015秋•迁安市期中）钟表在3点40分时，它的时针和分针所成的角是　 ．‎ ‎8．一个角的余角比它的补角还多，则这个角等于_______°.‎ ‎9．两个角，它们的比是3:2，其差为36°，则这两个角的关系是________.‎ ‎10．直角三角形的两个锐角的平分线所成的锐角为______.‎ ‎11．如图所示，∠A=50°，∠B=40°，∠C=30°，则∠BDC=________. ‎ ‎12．若三角形的两边长分别是2和7,则第三边长c的取值范围是_______.‎ 三、解答题 ‎13．如图，已知AB∥CD，∠B=65°，CM平分∠BCE，∠MCN=90°，求∠DCN的度数. 　　　　　　　　　　　　　　　　　　　　　 　 ‎ ‎14．如图，线段AB上的点数与线段的总数有如下关系：如果线段上有3个点时，线段共有3条；如果上有4个点时，线段共有6条；如果线段上有5个点时，线段共有10条；⑴当线段上有6个点时，线段共有多少条？⑵当线段上有n个点时，线段共有多少条？(用含n的代数式表示)⑶当n=100时，线段共有多少条？ 　　　　　　　　　　　　　 ‎ ‎15．如图，AE、OB、OC平分∠BAC、∠ABC、∠ACB，OD⊥BC，求证：∠1=∠2.‎ ‎16.（2015•同安区一模）已知△ABC三边长都是整数且互不相等，它的周长为12，当BC为最大边时，求∠A的度数．‎ ‎【答案与解析】‎ 一、选择题 ‎1.【答案】A.‎ ‎【解析】点到直线的线段中垂线段最短.‎ ‎2.【答案】C.‎ ‎【解析】每个点为端点的射线有两条.‎ ‎3.【答案】D.‎ ‎4.【答案】D.‎ ‎【解析】三角形内角和180°.‎ ‎5.【答案】B. ‎ ‎【解析】根据三角形的三边关系，得a﹣1+a＞a+1，解得a＞2．故选B．‎ ‎6.【答案】D. ‎ 二、填空题 ‎7．【答案】130　.‎ ‎【解析】提示： 3点40分时，它的时针和分针相距份，×30°=130°．故答案为：130．‎ ‎8．【答案】63°. ‎ ‎【解析】设补角为x，则余角为x+1°，因为一个角的补角比余角多90°，‎ 所以x-（x+1°）=90°，‎ 即x=117°，即该角为63°.‎ ‎9．【答案】互补.‎ ‎【解析】设两个角为3x，2x，即3x-2x=36°，x=36°，则3x+2x=180°.‎ ‎10．【答案】45°.‎ ‎11．【答案】120°.‎ ‎【解析】做射线AD，即∠BDC=∠1+∠2=∠3+∠B+∠4+∠C=∠B+∠A+∠C=120°.‎ ‎12．【答案】5＜c＜9．‎ ‎【解析】三角形的两边长分别是2和7, 则第三边长c的取值范围是│2-7│＜c＜2+7,即 5＜c＜9．‎ 三、解答题 ‎13.【答案与解析】32.5°.‎ 提示：利用角分线和平行线的性质可得. ‎ ‎14.【答案与解析】(1)15，提示：n=3,3条；n=4,6条；n=5,10条；可推出n=6，有15条；‎ ‎(2)，提示：通过总结n=3,4,5,6等几种特殊情况，可以归纳推得；‎ ‎(3)4950.提示：代入（2）中的公式可得.‎ ‎15.【答案与解析】∵AE、OB平分∠BAC、∠ABC，‎ ‎∴∠1=（∠ABC+∠CAB）=(180°-∠ACB)=90°-∠ACB，‎ 又∵OC平分∠ACB，OD⊥BC，‎ ‎∴∠2=90°-∠OCB=90°-∠ACB.‎ 即∠1=∠2.‎ ‎16.【答案与解析】解：根据题意，设BC、AC、AB边的长度分别是a、b、c，‎ 则a+b+c=12；‎ ‎∵BC为最大边，‎ ‎∴a最大，‎ 又∵b+c＞a，‎ ‎∴a＜6，‎ ‎∵△ABC三边长都是整数，‎ ‎∴a=5，‎ 又∵△ABC三边长互不相等，‎ ‎∴其他两边分别为3，4，‎ ‎∵32+42=52，‎ ‎∴△ABC是直角三角形，‎ ‎∴∠A=90°，‎ 即∠A的度数是90°．‎