中考数学模拟试题汇编专题25矩形菱形与正方形含答案 50页

矩形菱形与正方形 一、选择题 ‎1．(2016·浙江杭州萧山区·模拟)下列命题中，正确的是（　　）‎ A．菱形的对角线相等 B．平行四边形既是轴对称图形，又是中心对称图形 C．正方形的对角线相等且互相垂直 D．矩形的对角线不能相等 ‎【考点】命题与定理．‎ ‎【分析】根据菱形的性质对A进行判断；根据平行四边形的性质和轴对称的定义对B进行判断；根据正方形的性质对C进行判断；根据矩形的性质对D进行判断．‎ ‎【解答】解：A、菱形的对角线相互垂直平分，所以A选项错误；‎ B、平行四边形不是轴对称图形，只是中心对称图形，所以B选项错误；‎ C、正方形的对角线相等且互相垂直，所以C选正确；‎ D、矩形的对角线相等，所以D选项错误．‎ 故选C．‎ ‎【点评】本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．‎ ‎2. 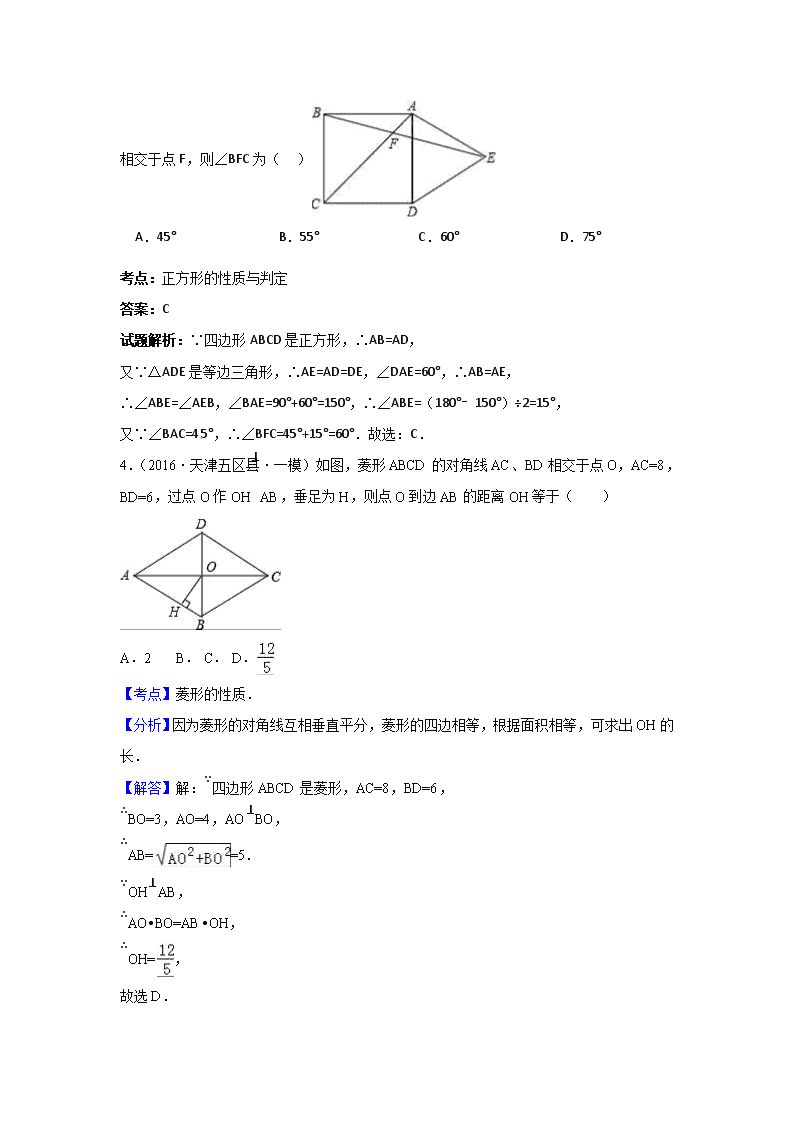（2016·绍兴市浣纱初中等六校·5月联考模拟）如图，矩形ABCD，点E在AD边上，过点E作AB的平行线，交BC于点F，将矩形ABFE绕着点E逆时针旋转60°，如果点F的对应点M落在边CD上，点B的对应点N落在边BC上，则（ ▲ ）‎ A． B． ‎ ‎ C． D．‎ ‎3．（2016·天津南开区·二模）‎ 如图，在正方形ABCD的外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为（    ）‎ A．45° B．55° C．60° D．75°‎ 考点：正方形的性质与判定 答案：C 试题解析：∵四边形ABCD是正方形，∴AB=AD，‎ 又∵△ADE是等边三角形，∴AE=AD=DE，∠DAE=60°，∴AB=AE，‎ ‎∴∠ABE=∠AEB，∠BAE=90°+60°=150°，∴∠ABE=（180°﹣150°）÷2=15°，‎ 又∵∠BAC=45°，∴∠BFC=45°+15°=60°．故选：C．‎ ‎4．（2016·天津五区县·一模）如图，菱形ABCD的对角线AC、BD相交于点O，AC=8，BD=6，过点O作OH⊥AB，垂足为H，则点O到边AB的距离OH等于（　　）‎ A．2 B． C． D．‎ ‎【考点】菱形的性质．‎ ‎【分析】因为菱形的对角线互相垂直平分，菱形的四边相等，根据面积相等，可求出OH的长．‎ ‎【解答】解：∵四边形ABCD是菱形，AC=8，BD=6，‎ ‎∴BO=3，AO=4，AO⊥BO，‎ ‎∴AB==5．‎ ‎∵OH⊥AB，‎ ‎∴AO•BO=AB•OH，‎ ‎∴OH=，‎ 故选D．‎ ‎【点评】本题考查菱形的基本性质，菱形的对角线互相垂直平分，菱形的四边相等，根据面积相等，可求出AB边上的高OH．‎ 答案：B ‎5．(2016·山西大同 ·一模）如图，正方形AEFG的边AE放置在正方形ABCD的对角线AC上，‎ EF与CD交于点M，得四边形AEMD，且两正方形的边长均为2，则两正方形重合部分（阴影部 第5题图 分）的面积为（ ）‎ A． ‎ B． ‎ ‎ C． D．‎ 答案：A ‎6．(2016·山西大同 ·一模）如图：正方形ABCD的对角线BD长为。若直线l满足：①点D到直线l的距离为 ，②A、C两点到直线l的距离相等，则符合题意的直线l的条数为（ ）‎ A．1 B．‎2 ‎ C．3 D．4‎ 答案：C ‎7．(2016·云南省曲靖市罗平县·二模)如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH=（　　）‎ A． B． C．12 D．24‎ ‎【考点】菱形的性质．‎ ‎【分析】设对角线相交于点O，根据菱形的对角线互相垂直平分求出AO、BO，再利用勾股定理列式求出AB，然后根据菱形的面积等对角线乘积的一半和底乘以高列出方程求解即可．‎ ‎【解答】解：如图，设对角线相交于点O，‎ ‎∵AC=8，DB=6，‎ ‎∴AO=AC=×8=4，‎ BO=BD=×6=3，‎ 由勾股定理的，AB===5，‎ ‎∵DH⊥AB，‎ ‎∴S菱形ABCD=AB•DH=AC•BD，‎ 即5DH=×8×6，‎ 解得DH=．‎ 故选A．‎ ‎【点评】本题考查了菱形的性质，勾股定理，主要利用了菱形的对角线互相垂直平分的性质，难点在于利用菱形的面积的两种表示方法列出方程．‎ ‎8．(2016·山东枣庄·模拟)如图，在半径为‎6cm的⊙O中，点A是劣弧的中点，点D是优弧上一点，且∠D=30°，下列四个结论：‎ ‎①OA⊥BC；②BC=6；③sin∠AOB=；④四边形ABOC是菱形．‎ 其中正确结论的序号是（　　）‎ A．①③ B．①②③④ C．②③④ D．①③④‎ ‎【考点】垂径定理；菱形的判定；圆周角定理；解直角三角形．‎ ‎【专题】几何图形问题．‎ ‎【分析】分别根据垂径定理、菱形的判定定理、锐角三角函数的定义对各选项进行逐一判断即可．‎ ‎【解答】解：∵点A是劣弧的中点，OA过圆心，‎ ‎∴OA⊥BC，故①正确；‎ ‎∵∠D=30°，‎ ‎∴∠ABC=∠D=30°，‎ ‎∴∠AOB=60°，‎ ‎∵点A是劣弧的中点，‎ ‎∴BC=2CE，‎ ‎∵OA=OB，‎ ‎∴OA=OB=AB=‎6cm，‎ ‎∴BE=AB•cos30°=6×=‎3cm，‎ ‎∴BC=2BE=‎6cm，故②正确；‎ ‎∵∠AOB=60°，‎ ‎∴sin∠AOB=sin60°=，‎ 故③正确；‎ ‎∵∠AOB=60°，‎ ‎∴AB=OB，‎ ‎∵点A是劣弧的中点，‎ ‎∴AC=AB，‎ ‎∴AB=BO=OC=CA，‎ ‎∴四边形ABOC是菱形，‎ 故④正确．‎ 故选：B．‎ ‎【点评】本题考查了垂径定理、菱形的判定、圆周角定理、解直角三角形，综合性较强，是一道好题．‎ B A C D 第9题图 ‎9. (2016·陕西师大附中·模拟)如图，在菱形ABCD中，AB = 5，∠BCD = 120°，则对角线AC等于（ ）‎ A. ‎20 　 B. ‎15　 ‎C. 10 D. 5 ‎ ‎【答案】D ‎10．（2016·河南洛阳·一模）如图4，正方形ABCD的边长为4，点P、Q分别是CD、AD的中点，动点E从点A向点B运动，到点B时停止运动；同时，动点F从点P出发，沿P→D→Q运动，点E、F的运动速度相同．设点E的运动路程为x，△AEF的面积为y，能大致刻画y与x的函数关系的图象是【 】‎ ‎ 答案：B ‎11. （2016·辽宁丹东七中·一模） 下列说法不正确的是（ ）‎ A．一组邻边相等的矩形是正方形 B．对角线相等的菱形是正方形 C．对角线互相垂直的矩形是正方形 D．有一个角是直角的平行四边形是正方形 答案：D ‎12.（2016·河大附中·一模）如图，在△ABC中，AD平分∠BAC，按如下步骤作图：第一步，分别以点A.D为圆心，以大于AD的长为半径在AD两侧作 弧，交于两点M、N;‎ 第二步，连接MN分别交AB、AC于点E、F;第三步，连接DE、DF.若BE=8，ED =4，CD=3，则BD的长是 ( )‎ ‎ A．4 B．‎6 C．8 D．12‎ 第12题 答案：B ‎13.（2016·黑龙江大庆·一模）下列命题 ：①等腰三角形的角平分线平分对边；②对角线垂直且相等的四边形是正方形；③正六边形的边心距等于它的边长；④过圆外一点作圆的两条切线，其切线长相等．其中真命题有（ ）个．‎ A．1个 B．2个 C．3个 D．4个 答案：A ‎14.（2016·湖北襄阳·一模）如图，已知菱形ABCD的对角线AC．BD的长分别为‎6cm、‎8cm，AE⊥BC于点E，则AE的长是（　　）　‎ ‎ A． B． C． D．‎ ‎ 第14题 答案：D ‎15.（2016·广东东莞·联考）‎ 为增加绿化面积，某小区将原来正方形地砖更换为如图所示的正八边形植草砖，更换后，图中阴影部分为植草区域，设正八边形与其内部小正方形的边长都为a，则阴影部分的面积为（　　）‎ A．‎2a2 B．‎3a2 ‎C．‎4a2 D．‎5a2‎ ‎【考点】正多边形和圆；等腰直角三角形；正方形的性质．‎ ‎【分析】根据正八边形的性质得出∠CAB=∠CBA=45°，进而得出AC=BC=a，再利用正八边形周围四个三角形的特殊性得出阴影部分面积即可．‎ ‎【解答】解：∵某小区将原来正方形地砖更换为如图所示的正八边形植草砖，设正八边形与其内部小正方形的边长都为a，‎ ‎∴AB=a，且∠CAB=∠CBA=45°，‎ ‎∴sin45°===，‎ ‎∴AC=BC=a，‎ ‎∴S△ABC=×a×a=，‎ ‎∴正八边形周围是四个全等三角形，面积和为：×4=a2．‎ 正八边形中间是边长为a的正方形，‎ ‎∴阴影部分的面积为：a2+a2=‎2a2，‎ 故选：A．‎ ‎【点评】此题主要考查了正八边形的性质以及等腰直角三角形的性质，根据已知得出S△ABC的值是解题关键．‎ ‎16.（2016·广东深圳·一模）下列命题中是假命题的是（　　）‎ A．一组对边平行且相等的四边形是平行四边形 B．一组对边相等且有一个角是直角的四边形是矩形 C．一组邻边相等的平行四边形是菱形 D．一组邻边相等的矩形是正方形 ‎【考点】正方形的判定；平行四边形的判定；菱形的判定；矩形的判定．‎ ‎【专题】证明题．‎ ‎【分析】做题时首先熟悉各种四边形的判定方法，然后作答．‎ ‎【解答】解：A、一组对边平行且相等的四边形是平行四边形（平行四边形判定定理）；故A不符合题意．‎ B、一组对边相等且有一个角是直角的四边形，不一定是矩形，还可能是不规则四边形，故B符合题意．‎ C、一组邻边相等的平行四边形是菱形，故C不符合题意；‎ D、一组邻边相等的矩形是正方形，故D不符合题意．‎ 故选：B．‎ ‎【点评】本题主要考查各种四边形的判定，基础题要细心．‎ ‎17.（2016·广东深圳·联考）正方形ABCD的一条对角线长为8，则这个正方形的面积是 A． B．‎32 ‎C．64 D．128‎ 答案：B ‎18.（2016·广东深圳·联考）如图，矩形ABCD中，AE平分∠BAD交BC于E，∠CAE=15°，则下列结论：‎ ① ‎△ODC是等边三角形； ②BC=2AB；‎ ‎③∠AOE=135°； ④S△AOE=S△COE，‎ 其中正确的结论的个数有 A．1 B．‎2 C．3 D．4‎ 答案：C C B A D ‎19.（2016·河南三门峡·二模） 如图，小明在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于的长为半径画弧，两弧相交于C、D两点，直线CD即为所求．根据他的作图方法可知四边形ADBC一定是（　　）‎ A．矩形 B．菱形 C．正方形 D．无法确定 答案：B ‎20.（2016·河南三门峡·一模）菱形的边长是10，一条对角线长是12，则此菱形的另一条对角线是( )‎ A. 10 B. ‎24 C. 8 D. 16‎ 答案：D ‎（第1题）‎ 二、填空题 ‎1．（2016·天津市和平区·一模）长为1，宽为a的矩形纸片（＜a＜1），如图那样折一下，剪下一个边长等于矩形宽度的正方形（称为第一次操作）；再把剩下的矩形如图那样折一下，剪下一个边长等于此时矩形宽度的正方形（称为第二次操作）；如此反复操作下去，若在第n次操作后，剩下的矩形为正方形，则操作终止．‎ ‎（I）第二次操作时，剪下的正方形的边长为　1﹣a　；‎ ‎（Ⅱ）当n=3时，a的值为　或　．（用含a的式子表示）‎ ‎【考点】翻折变换（折叠问题）．‎ ‎【分析】根据操作步骤，可知每一次操作时所得正方形的边长都等于原矩形的宽．所以首先需要判断矩形相邻的两边中，哪一条边是矩形的宽．当＜a＜1时，矩形的长为1，宽为a，所以第一次操作时所得正方形的边长为a，剩下的矩形相邻的两边分别为1﹣a，a．由1﹣a＜a可知，第二次操作时所得正方形的边长为1﹣a，剩下的矩形相邻的两边分别为1﹣a，a﹣（1﹣a）=‎2a﹣1．由于（1﹣a）﹣（‎2a﹣1）=2﹣‎3a，所以（1﹣a）与（‎2a﹣1）的大小关系不能确定，需要分情况进行讨论．又因为可以进行三次操作，故分两种情况：①1﹣a＞‎2a﹣1；②1﹣a＜‎2a﹣1．对于每一种情况，分别求出操作后剩下的矩形的两边，根据剩下的矩形为正方形，列出方程，求出a的值．‎ ‎【解答】解：由题意，可知当＜a＜1时，第一次操作后剩下的矩形的长为a，宽为1﹣a，所以第二次操作时正方形的边长为1﹣a，第二次操作以后剩下的矩形的两边分别为1﹣a，‎2a﹣1．‎ 故答案为：1﹣a；‎ 此时，分两种情况：‎ ‎①如果1﹣a＞‎2a﹣1，即a＜，那么第三次操作时正方形的边长为‎2a﹣1．‎ ‎∵经过第三次操作后所得的矩形是正方形，‎ ‎∴矩形的宽等于1﹣a，‎ 即‎2a﹣1=（1﹣a）﹣（‎2a﹣1），解得a=；‎ ‎②如果1﹣a＜‎2a﹣1，即a＞，那么第三次操作时正方形的边长为1﹣a．‎ 则1﹣a=（‎2a﹣1）﹣（1﹣a），解得a=．‎ 故答案为：或．‎ ‎【点评】本题考查了一元一次方程的应用，解题的关键是分两种情况：①1﹣a＞‎2a﹣1；②1﹣a＜‎2a﹣1．分别求出操作后剩下的矩形的两边．‎ ‎2．（2016·天津市南开区·一模）如图，在正方形ABCD内有一折线段，其中AE丄EF，EF丄FC，并且AE=6，EF=8，FC=10，则正方形与其外接圆之间形成的阴影部分的面积为　80π﹣160　．‎ ‎【考点】相似三角形的判定与性质；勾股定理；正方形的性质．‎ ‎【专题】压轴题．‎ ‎【分析】首先连接AC，则可证得△AEM∽△CFM，根据相似三角形的对应边成比例，即可求得EM与FM的长，然后由勾股定理求得AM与CM的长，则可求得正方形与圆的面积，则问题得解．‎ ‎【解答】解：连接AC，‎ ‎∵AE丄EF，EF丄FC，‎ ‎∴∠E=∠F=90°，‎ ‎∵∠AME=∠CMF，‎ ‎∴△AEM∽△CFM，‎ ‎∴，‎ ‎∵AE=6，EF=8，FC=10，‎ ‎∴，‎ ‎∴EM=3，FM=5，‎ 在Rt△AEM中，AM==3，‎ 在Rt△FCM中，CM==5，‎ ‎∴AC=8，‎ 在Rt△ABC中，AB=AC•sin45°=8•=4，‎ ‎∴S正方形ABCD=AB2=160，‎ 圆的面积为：π•（）2=80π，‎ ‎∴正方形与其外接圆之间形成的阴影部分的面积为80π﹣160．‎ 故答案为：80π﹣160．‎ ‎【点评】此题考查了相似三角形的判定与性质，正方形与圆的面积的求解方法，以及勾股定理的应用．此题综合性较强，解题时要注意数形结合思想的应用．‎ ‎3．(2016·浙江镇江·模拟)如图，P是菱形ABCD对角线BD上的一点，PE⊥BC于点E，PE=‎4cm，则点P到直线AB的距离等于 　cm.‎ 答案：4‎ ‎4．(2016·重庆巴南 ·一模）如图，正方形ABCD中，点E、F分别是BC、CD边上的点，且∠EAF=45°，对角线BD交AE于点M，交AF于点N．若AB=4，BM=2，则MN的长为　 　．‎ ‎【分析】延长BC到G，使BG=DF连接AG，在AG截取AH=AN，连接MH、BH，证得Rt△ABG≌Rt△ADF，△AMN≌△AMH，△DFN≌△BGH，△AEF≌△AEG，最后利用等量代换求得答案即可．‎ ‎【解答】解：如图，延长BC到G，使BG=DF连接AG，在AG截取AH=AN，连接MH、BH．‎ ‎∵四边形ABCD为正方形，‎ ‎∴AB=BC=CD=AD，∠4=∠5=45°，∠BAD=∠ADF=∠ABE=∠ABG=90°，‎ 在RT△ABG和RT△ADF中，‎ ‎，‎ ‎∴Rt△ABG≌Rt△ADF（SAS），‎ ‎∴∠1=∠2，∠7=∠G，AF=AG，‎ ‎∴∠GAE=∠2+∠3=∠1+∠3=∠BAD﹣∠EAF=90°﹣45°=45°=∠EAF，‎ 在△AMN和△AMH中，‎ ‎，‎ ‎∴△AMN≌△AMH（SAS），‎ ‎∴MN=MH，‎ ‎∵AF=AG，AN=AH，‎ ‎∴FN=AF﹣AN=AG﹣AH=GH，‎ 在△DFN和△BFH中，‎ ‎，‎ ‎∴△DFN≌△BGH（SAS），‎ ‎∴∠6=∠4=45°，DN=BH，‎ ‎∴∠MBH=∠ABH+∠5=∠ANG﹣∠6+∠5=90°﹣45°+45°=90°‎ ‎∴BM2+DN2=BM2+BH2=MH2=MN2，‎ ‎∵BD=AB=8，‎ ‎∴22+（8﹣2﹣MN）2=MN2，‎ ‎∴MN=．‎ 故答案为：．‎ ‎5．(2016·山东枣庄·模拟)如图，点E在正方形ABCD的边CD上．若△ABE的面积为8，CE=3，则线段BE的长为　5　．‎ ‎【考点】正方形的性质；三角形的面积；勾股定理．‎ ‎【分析】根据正方形性质得出AD=BC=CD=AB，根据面积求出EM，得出BC=4，根据勾股定理求出即可．‎ ‎【解答】解：‎ 过E作EM⊥AB于M，‎ ‎∵四边形ABCD是正方形，‎ ‎∴AD=BC=CD=AB，‎ ‎∴EM=AD，BM=CE，‎ ‎∵△ABE的面积为8，‎ ‎∴×AB×EM=8，‎ 解得：EM=4，‎ 即AD=DC=BC=AB=4，‎ ‎∵CE=3，‎ 由勾股定理得：BE===5，‎ 故答案为：5．‎ ‎【点评】本题考查了三角形面积，正方形性质，勾股定理的应用，解此题的关键是求出BC的长，难度适中．‎ ‎6. （2016·江苏省南京市钟爱中学·九年级下学期期初考试）如图，在△ABC中，AH⊥BC于H，正方形DEFG内接于△ABC，点D、E分别在边AB、AC上，点G、F在边BC上．如果BC=20，正方形DEFG的面积为25，那么AH的长是　　　　　　．‎ 答案：　　‎ ‎7．（2016·河南洛阳·一模）如图6，在平面直角坐标系中，直线y= -3x+3与x轴、y轴分别交干A、B两点，以AB为边在第一象限作正方形ABCD，点D在双曲线y=(k≠0)上，将正方形沿x轴负方向平移a个单位长度后，点C恰好落在该双曲线上，则a的值是 .‎ 答案： 2‎ ‎8.（2016·河南洛阳·一模）在矩形ABCD中，AB=4,BC=3，点P在AB上。若将△DAP沿DP折叠，使点A落在矩形对角线上的A'处，则AP的长为 ．‎ 答案：或 附：详解：‎ ‎①点A落在矩形对角线BD上，如图1，∵AB=4，BC=3，∴BD=5， ‎ 根据折叠的性质，AD=A′D=3，AP=A′P，∠A=∠PA′D=90°，∴BA′=2，设AP=x，‎ 则BP=4－x，∵BP2=BA′2+PA′2， ∴（4－x）2=x2+22，解得：x=， ∴AP=；‎ C D A P B A′‎ A P B D C A′‎ E 图1‎ 图2‎ ‎②点A落在矩形对角线AC上，如图2，根据折叠的性质可知DP⊥AC，∴△DAP∽△ABC， ∴， ∴．‎ ‎ 故答案为：或． ‎ ‎9.（2016·辽宁丹东七中·一模） 小明尝试着将矩形纸片ABCD（如图①，AD>CD）沿过A点的直线折叠，使得B点落在AD边上的点F处，折痕为AE（如图②）；再沿过D点的直线折叠，使得C点落在DA边上的点N处，E点落在AE边上的点M处，折痕为DG（如图③）．如果第二次折叠后，M点正好在∠NDG的平分线上，那么矩形ABCD长与宽的比值为 ．‎ A B C D A B C D E F ‎①‎ ‎②‎ A B C D E G M N ‎③‎ 答案：‎ ‎10.（2016·辽宁丹东七中·一模）如图，将矩形纸片ABC（D）折叠，使点（D）与点B重合，点C落在点处，折痕为EF，若，那么的度数为 ‎ 度。‎ 答案：125º ‎ ‎11.（2016·河大附中·一模）在菱形ABCD中，AB=5，AC=8，点P是AC上的一个动点，过点P作EF垂直于AC交AD于点E，交AB于点F，将△AEF沿EF折叠，使点A落在点A'处，当△A'CD是直角三角形时，AP的长为 .‎ 答案：2或 ‎12.（2016·黑龙江齐齐哈尔·一模）四边形ABCD的对角线AC、BD相交于点O，AD∥BC，AC=BD.试添加一个条件_________________，使四边形ABCD为矩形．‎ 答案： BC=AD或AB∥CD或∠BAC=∠ACD或∠ABD=∠BDC或OB=OD或OA=OC等. (AC与BD互相平分是两个条件，故不给分) ‎ 第13题 ‎13.（2016·黑龙江齐齐哈尔·一模）如图，矩形ABCD 的边长AB=8，AD=4，若将△DCB沿BD所在直线翻折，点C落在点F处，DF与AB交于点E. 则cos∠ADE = ．‎ 答案： ‎ ‎14.（2016·广东·一模）如图，已知正方形ABCD的边长为2，E是边BC上的动点，BF⊥AE交CD于点F，垂足为G，连结CG．下列说法：①AG＞GE；②AE=BF；③点G运动的路径长为π；④CG的最小值为﹣1．其中正确的说法是　 　．（把你认为正确的说法的序号都填上）‎ 答案：②③‎ ‎15.（2016·广东东莞·联考）将正方形与直角三角形纸片按如图所示方式叠放在一起，已知正方形的边长为‎20cm，点O为正方形的中心，AB=‎5cm，则CD的长为　‎20　cm．‎ ‎【考点】正方形的性质；相似三角形的判定与性质．‎ ‎【分析】根据题意四边形BOCE是正方形，且边长等于大正方形的边长的一半，等于‎10cm，再根据△DCE和△DOA相似，利用相似三角形对应边成比例列式求解即可．‎ ‎【解答】解：如图，‎ ‎∵点O为正方形的中心，‎ ‎∴四边形BOCE是正方形，边长=20÷2=‎10cm，‎ ‎∵CE∥AO，‎ ‎∴△DCE∽△DOA，‎ ‎∴，‎ 即，‎ 解得DC=‎20cm．‎ 故答案为：20．‎ ‎【点评】本题主要考查正方形各边都相等，每个角都是直角的性质和相似三角形对应边成比例的性质，需要熟练掌握并灵活运用．‎ ‎16.（2016•广东•一模）如图，已知正方形ABCD的边长为2，E是边BC上的动点，BF⊥AE交CD于点F，垂足为G，连结CG．下列说法：①AG＞GE；②AE=BF；③点G运动的路径长为π；④CG的最小值为 ﹣1．其中正确的说法是　 　．（把你认为正确的说法的序号都填上）‎ 答案：②③‎ ‎17.（2016•广东东莞•联考）将正方形与直角三角形纸片按如图所示方式叠放在一起，已知正方形的边长为‎20cm，点O为正方形的中心，AB=‎5cm，则CD的长为　‎20　cm．‎ 答案：20． 18.（2016•广东河源•一模）如图，矩形ABCD的对角线AC，BD相交于点O，CE∥BD，‎ DE∥AC，若AC = ‎4 cm，则四边形CODE的周长为 。 ‎ 答案：‎‎8 cm ‎19. （2016•广东深圳•联考）如图，已知矩形OABC与矩形ODEF是位似图形，P是位似中心，若点B的坐标为（2，4），点E的坐标为（﹣1，2），则点P的坐标为　 ‎ 答案：（-2，0）‎ ‎20.（2016·广东河源·一模）如图，矩形ABCD的对角线AC，BD相交于点O，CE∥BD，DE∥AC，若AC = ‎4 cm，则四边形CODE的周长为 。 ‎ 答案：‎‎8 cm ‎21.（2016·广东河源·一模）如图，三个小正方形的边长都为1，则图中阴影部分面积的和是__________。（结果保留π）‎ 答案：‎ ‎22. （2016·广东深圳·联考）如图，已知矩形OABC与矩形ODEF是位似图形，P是位似中心，若点B的坐标为（2，4），点E的坐标为（﹣1，2），则点P的坐标为　 　‎ 答案：（-2，0）‎ ‎23. （2016·广东深圳·联考）如图，矩形ABCD中，AD=4，∠CAB=30o，点P 是线段AC上的动点，点Q是线段CD上的动点，则AQ+QP的最小值是　 　‎ ‎ 答案：‎ 三、解答题 ‎1．(2016·浙江镇江·模拟)（本小题满分6分）‎ 如图，E、F分别是□ABCD的边BC、AD上的中点.‎ ‎（1） 求证：△ABE≌△CDF；‎ ‎（2） 当∠BAC= ° 时，四边形AECF是菱形.‎ ‎（1） 证明：在□ABCD中，AD=BC，AB=CD，∠B=∠D，‎ ‎∵E、F分别是□ABCD的边BC、AD上的中点,‎ ‎∴BE=BC，DF=AD，则BE= DF. ‎ 在△ABE和△CDF中，BE= DF，∠B=∠D，AB=CD，‎ 则△ABE≌△CDF；‎ ‎（2） 当∠BAC= 90 ° 时，四边形AECF是菱形. ‎ ‎2.（2016齐河三模）如图，正方形ABCD中，点E，F分别在边AB，BC上，AF＝DE，AF和DE相交于点G.‎ ‎(1)观察图形，写出图中所有与∠AED相等的角；‎ ‎(2)选择图中与∠AED相等的任意一个角，并加以证明．‎ 答案：（1）由图可知，∠DAG，∠AFB，∠CDE与∠AED相等；‎ ‎（2）选择∠DAG=∠AED，证明如下：‎ ‎∵正方形ABCD，‎ ‎∴∠DAB=∠B=90°，AD=AB，‎ ‎∵AF=DE，‎ 在△DAE与△ABF中，‎ ‎，‎ ‎∴△DAE≌△ABF（SAS），‎ ‎∴∠ADE=∠BAF，‎ ‎∵∠DAG+∠BAF=90°，∠GDA+∠AED=90°，‎ ‎∴∠DAG=∠AED．‎ ‎3.（2016青岛一模）已知：如图，在矩形ABCD中，点E在边AD上，点F在边BC上，且AE=CF，作EG∥FH，分别与对角线BD交于点G、H，连接EH，FG．‎ ‎（1）求证：△BFH≌△DEG；‎ ‎（2）连接DF，若BF=DF，则四边形EGFH是什么特殊四边形？证明你的结论．‎ ‎【考点】矩形的性质；全等三角形的判定与性质；菱形的判定．‎ ‎【分析】（1）由平行四边形的性质得出AD∥BC，AD=BC，OB=OD，由平行线的性质得出∠FBH=∠EDG，∠OHF=∠OGE，得出∠BHF=∠DGE，求出BF=DE，由AAS即可得出结论；‎ ‎（2）先证明四边形EGFH是平行四边形，再由等腰三角形的性质得出EF⊥GH，即可得出四边形EGFH是菱形．‎ ‎【解答】（1）证明：∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC，AD=BC，OB=OD，‎ ‎∴∠FBH=∠EDG，‎ ‎∵AE=CF，‎ ‎∴BF=DE，‎ ‎∵EG∥FH，‎ ‎∴∠OHF=∠OGE，‎ ‎∴∠BHF=∠DGE，‎ 在△BFH和△DEG中，‎ ‎，‎ ‎∴BFH≌△DEG（AAS）；‎ ‎（2）解：四边形EGFH是菱形；理由如下：‎ 连接DF，如图所示：‎ 由（1）得：BFH≌△DEG，‎ ‎∴FH=EG，‎ 又∵EG∥FH，‎ ‎∴四边形EGFH是平行四边形，‎ ‎∵BF=DF，OB=OD，‎ ‎∴EF⊥BD，‎ ‎∴EF⊥GH，‎ ‎∴四边形EGFH是菱形．‎ ‎4．（2016·天津南开区·二模）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE.易证:CE=CF.‎ ‎(1)在图1中，若G在AD上，且∠GCE=450.试猜想GE，BE，GD三线段之间的数量关系，并证明你的结论.‎ ‎(2)运用(1)中解答所积累的经验和知识，完成下面两题：‎ ‎①如图2，在四边形ABCD中∠B=∠D=900，BC=CD，点E，点G分别是AB边，AD边上的动点.若∠BCD=α，∠ECG=β，试探索当α和β满足什么关系时，图1中GE，BE，GD三线段之间的关系仍然成立，并说明理由.‎ ‎②在平面直角坐标中，边长为1的正方形OABC的两顶点A，C分别在y轴、x轴的正半轴上，点O在原点．现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y=x上时停止旋转，旋转过程中，AB边交直线y=x于点M，BC边交x轴于点N(如图3).设△MBN的周长为p，在旋转正方形OABC的过程中，p值是否有变化？若不变，请直接写出结论．‎ 考点：四边形综合题 答案：见解析 试题解析：（1）∵在△EBC和△FDC中，∴△EBC≌△FDC，∴∠DCF=∠BCE，‎ ‎∵∠GCE=45°，∴∠BCE+∠DCG=90°﹣45°=45°，即∠DCG+∠DCF=45°，∴GC=GC，ECG=∠FCG，‎ 在△ECG和△FCG中，，∴△ECG≌△FCG，∴EG=GF，即GE=BE+GD．‎ ‎（2）①α=2β．如图，‎ 延长AD到F点，使DF=BE，连接CF，可证△EBC≌△FDC，‎ 则∠BCE+∠DCG=∠GCF，由α=2β可知∠ECG=∠GCF，可证△ECG≌△FCG，故EG=GF，即GE=BE+GD．‎ ‎②在旋转正方形OABC的过程中，P值无变化．证明：如图，‎ 延长BA交y轴于E点，则∠AOE=45°﹣∠AOM，∠CON=90°﹣45°﹣∠AOM=45°﹣∠AOM，‎ ‎∴∠AOE=∠CON．又∵OA=OC，∠OAE=180°﹣90°=90°=∠OCN．‎ 在△OAE和△OCN中，．∴△OAE≌△OCN（ASA）．∴OE=ON，AE=CN．‎ 在△OME和△OMN中．∴△OME≌△OMN（SAS）．∴MN=ME=AM+AE．‎ ‎∴MN=AM+CN，∴P=MN+BN+BM=AM+CN+BN+BM=AB+BC=2．‎ ‎∴在旋转正方形OABC的过程中，P值无变化．‎ 5． ‎(2016·山西大同 ·一模）如图，已知：AB是的弦，CD是的直径，CD⊥AB，‎ 垂足为E，且点E是OD的中点，的切线BM与AO的延长线相交于点M，连接AC、CM ‎（1）若AB=，求的半径及弧AB的长度.‎ ‎（2）求证：四边形ABMC是菱形.‎ 答案：‎ 解（1）连接OB ‎ ∵OA=OB，E是AB的中点 ‎ ∴∠AOE=∠BOE, OE⊥AB ‎ 又∵OE=OA ‎ ∴∠OAB=30°，∠AOE=60°‎ 设AO为x，则OE=x ‎∴x=4‎ ‎∴弧AB长l= ‎ ‎（2）由（1）∠OAB=∠OBA=30°‎ ‎ ∠BOM=∠COM=60°，∠AMB=30°‎ ‎∴AB=BM 在△COM和△BOM中 ‎ OC=‎OB ‎ ∠COM=∠BOM ‎ OM=OM ‎∴△COM≌△BOM（SAS）‎ ‎∴CM=BM=AB ‎ ‎ ‎∴AB∥CM ‎∴ABCD是菱形 ‎6．(2016·山西大同 ·一模）问题情境：如图将边长为‎8cm的正方形纸片ABCD折叠，使点B恰好落在AD边的中点F处，折痕EG分别交AB、CD于点E、G，FN与DC交于点M，连接BF交EG于点P.‎ 独立思考：‎ ‎（1）AE=_______cm，△FDM的周长为_____cm ‎（2）猜想EG与BF之间的位置关系与数量关系，‎ 并证明你的结论.‎ 拓展延伸：‎ 如图2，若点F不是AD的中点，且不与点A、D重合：‎ ‎ ①△FDM的周长是否发生变化，并证明你的结论.‎ ‎②判断（2）中的结论是否仍然成立，若不成立请直接写出新的结论（不需证明）.‎ 答案：‎ ‎ （1）3， 16‎ ‎(2)EG⊥BF, EG=BF 则∠EGH+∠GEB=90°‎ 由折叠知，点B、F关于直线GE所在直线对称 ‎∴∠FBE=∠EGH ‎∵ABCD是正方形 ‎∴AB=BC ∠C=∠ABC=90°‎ 四边形GHBC是矩形，∴GH=BC=AB ‎∴△AFB全等△HEG ‎∴BF=EG ‎(3)①△FDM的周长不发生变化 由折叠知∠EFM=∠ABC=90°‎ ‎∴∠DFM+∠AFE=90°‎ ‎∵四边形ABCD为正方形，∠A=∠D=90°‎ ‎∴∠DFM+∠DMF=90°‎ ‎∴∠AFE=∠DMF ‎∴△AEF∽△DFM ‎∴‎ 设AF为x，FD=8-x ‎∴ ‎ ‎∴ ‎ △ FMD的周长=‎ ‎∴△FMD的周长不变 ‎②（2）中结论成立 ‎7．(2016·云南省曲靖市罗平县·二模)在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上，CE∥BF，连接BE、CF．‎ ‎（1）求证：△BDF≌△CDE；‎ ‎（2）若DE=BC，试判断四边形BFCE是怎样的四边形，并证明你的结论．‎ ‎【考点】矩形的判定；全等三角形的判定与性质．‎ ‎【分析】（1）根据平行线得出∠CED=∠BFD，根据AAS推出两三角形全等即可；‎ ‎（2）根据全等得出DE=DF，根据BD=DC推出四边形是平行四边形，求出∠BEC=90°，根据矩形的判定推出即可．‎ ‎【解答】（1）证明：∵CE∥BF，‎ ‎∴∠CED=∠BFD，‎ ‎∵D是BC边的中点，‎ ‎∴BD=DC，‎ 在△BDF和△CDE中 ‎，‎ ‎∴△BDF≌△CDE（AAS）；‎ ‎（2）四边形BFCE是矩形，‎ 证明：∵△BDF≌△CDE，‎ ‎∴DE=DF，‎ ‎∵BD=DC，‎ ‎∴四边形BFCE是平行四边形，‎ ‎∵BD=CD，DE=BC，‎ ‎∴BD=DC=DE，‎ ‎∴∠BEC=90°，‎ ‎∴平行四边形BFCE是矩形．‎ ‎【点评】本题考查了平行线性质，全等三角形的性质和判定，矩形的判定，平行四边形的判定的应用，注意：有一个角是直角的平行四边形是矩形．‎ ‎8．(2016·云南省·一模)如图，在△ABC中，DE分别是AB，AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连CF ‎（1）求证：四边形BCFE是菱形；‎ ‎（2）若CE=6，∠BEF=120°，求菱形BCFE的面积．‎ ‎【考点】菱形的判定与性质．‎ ‎【分析】（1）从所给的条件可知，DE是△ABC中位线，所以DE∥BC且2DE=BC，所以BC和EF平行且相等，所以四边形BCFE是平行四边形，又因为BE=FE，所以是菱形；‎ ‎（2）由∠BEF是120°，可得∠EBC为60°，即可得△BEC是等边三角形，求得BE=BC=CE=6，再过点E作EG⊥BC于点G，求的高EG的长，即可求得答案．‎ ‎【解答】（1）证明：∵D、E分别是AB、AC的中点，‎ ‎∴DE∥BC且2DE=BC，‎ 又∵BE=2DE，EF=BE，‎ ‎∴EF=BC，EF∥BC，‎ ‎∴四边形BCFE是平行四边形，‎ 又∵BE=EF，‎ ‎∴四边形BCFE是菱形；‎ ‎（2）解：∵∠BEF=120°，‎ ‎∴∠EBC=60°，‎ ‎∴△EBC是等边三角形，‎ ‎∴BE=BC=CE=6，‎ 过点E作EG⊥BC于点G，‎ ‎∴EG=BE•sin60°=6×=3，‎ ‎∴S菱形BCFE=BC•EG=6×3=18．‎ ‎【点评】本题考查菱形的判定和性质以及三角形中位线定理，以及菱形的面积的计算等知识点．注意证得△BEC是等边三角形是关键．‎ ‎9．(2016·云南省·二模)如图，四边形ABCD是矩形，点E是AD的中点，点F是BC的中点．求证：△ABF≌△CDE．‎ ‎【考点】矩形的性质；全等三角形的判定．‎ ‎【专题】证明题．‎ ‎【分析】由矩形的性质得出∠B=∠D=90°，AB=CD，AD=BC，由中点的定义得出BF=DE，由SAS证明△ABF≌△CDE即可．‎ ‎【解答】证明：∵四边形ABCD是矩形，‎ ‎∴∠B=∠D=90°，AB=CD，AD=BC，‎ ‎∵点E是AD的中点，点F是BC的中点，‎ ‎∴DE=AD BF=BC，‎ ‎∴BF=DE，‎ 在△ABF和△CDE中，‎ ‎，‎ ‎∴△ABF≌△CDE（SAS）．‎ ‎【点评】本题考查了矩形的性质、全等三角形的判定；熟练掌握矩形的性质，熟记全等三角形的判定方法SAS是解决问题的关键．‎ ‎10．(2016·山东枣庄·模拟)如图，已知△ABC内接于⊙O，且AB=AC，直径AD交BC于点E，F是OE上的一点，使CF∥BD．‎ ‎（1）求证：BE=CE；‎ ‎（2）试判断四边形BFCD的形状，并说明理由；‎ ‎（3）若BC=8，AD=10，求CD的长．‎ ‎【考点】垂径定理；勾股定理；菱形的判定．‎ ‎【分析】（1）证明△ABD≌△ACD，得到∠BAD=∠CAD，根据等腰三角形的性质即可证明；‎ ‎（2）菱形，证明△BFE≌△CDE，得到BF=DC，可知四边形BFCD是平行四边形，易证BD=CD，可证明结论；‎ ‎（3）设DE=x，则根据CE2=DE•AE列方程求出DE，再用勾股定理求出CD．‎ ‎【解答】（1）证明：∵AD是直径，‎ ‎∴∠ABD=∠ACD=90°，‎ 在Rt△ABD和Rt△ACD中，‎ ‎，‎ ‎∴Rt△ABD≌Rt△ACD，‎ ‎∴∠BAD=∠CAD，‎ ‎∵AB=AC，‎ ‎∴BE=CE；‎ ‎（2）四边形BFCD是菱形．‎ 证明：∵AD是直径，AB=AC，‎ ‎∴AD⊥BC，BE=CE，‎ ‎∵CF∥BD，‎ ‎∴∠FCE=∠DBE，‎ 在△BED和△CEF中 ‎，‎ ‎∴△BED≌△CEF，‎ ‎∴CF=BD，‎ ‎∴四边形BFCD是平行四边形，‎ ‎∵∠BAD=∠CAD，‎ ‎∴BD=CD，‎ ‎∴四边形BFCD是菱形；‎ ‎（3）解：∵AD是直径，AD⊥BC，BE=CE，‎ ‎∴CE2=DE•AE，‎ 设DE=x，‎ ‎∵BC=8，AD=10，‎ ‎∴42=x（10﹣x），‎ 解得：x=2或x=8（舍去）‎ 在Rt△CED中，‎ CD===2．‎ ‎【点评】本题主要考查了圆的有关性质：垂径定理、圆周角定理，三角形全等的判定与性质，菱形的判定与性质，勾股定理，三角形相似的判定与性质，熟悉圆的有关性质是解决问题的关键．‎ 11. ‎（2016·吉林东北师范大学附属中学·一模）（7分）如图，在中，平分，‎ 过点分别作、，分别交于点． 求证：四边形 是菱形．‎ ‎（第11题）‎ 答案：证明：∵、，‎ ‎∴四边形是平行四边形． ‎ ‎∵平分，‎ ‎∴． ‎ ‎∵，‎ ‎∴． ‎ ‎∴． ‎ ‎∴． ‎ ‎ ∴平行四边形是菱形． ‎ ‎12.（2016·吉林东北师范大学附属中学·一模）（9分）如图，将矩形绕点顺时针旋转，得到矩形，点的对应点恰好落在的延长线上，边交边于点．‎ ‎（1）求证：．‎ ‎（2）若，，求的长．‎ ‎（第12题）‎ 答案：解：（1）连结AC、，如图． ‎ ‎∵四边形ABCD为矩形，‎ ‎ ∴∠ABC90°，即．‎ 由旋转，得 ， ‎ ‎∴． ‎ ‎（2）∵四边形为矩形，‎ ‎∴． ‎ ‎∵，‎ ‎∴． ‎ 由旋转，得 ，‎ ‎∴．‎ ‎∵，‎ ‎∴≌． ‎ ‎∴．‎ 设，则．‎ 在中，，‎ 由勾股定理，得．‎ 解得．‎ ‎ ∴．‎ ‎13.（2016·江苏丹阳市丹北片·一模）（7分）已知：如图，正方形ABCD的边长为6，BM，DN分别平分正方形的两个外角，且满足∠MAN=45°，连接MC，NC，MN． （1）求证：BM•DN=36； （2）求∠MCN的度数；‎ 答案：（7分）（1）证明略（3分） （2）135度 （4分）‎ ‎14.（2016·上海市闸北区·中考数学质量检测4月卷）如图，矩形OMPN的顶点O在原点，M、N分别在轴和轴的正半轴上，OM=6，ON=3，反比例函数的图像与PN交于C，与PM交于D，过点C作CA⊥轴于点A，过点D作DB⊥轴于点B，AC与BD交于点G．‎ ‎（1）求证：AB//CD ；‎ ‎（2）在直角坐标平面内是否若存在点E，使以B、C、D、E为顶点，BC为腰的梯形是等腰梯形？若存在，求点E的坐标；若不存在请说明理由．‎ ‎（第14题图）‎ G O y A x B C D N P M 答案：解：∵矩形OMPN ，OM＝6，ON＝3‎ ‎∴点P（6，3）‎ ‎∵点C、D都在反比例函数图像上，‎ 且点C在PN上，点D在PM上，‎ ‎∴点C（2，3），点D（6，1）‎ ‎ 又DB⊥y轴，CA⊥x轴，‎ ‎∴A（2，0），B（0，1）‎ ‎∵BG＝2，GD＝4，CG＝2，AG＝1‎ ‎∴， ‎ ‎∴ ‎ ‎∴AB∥CD．‎ ‎ ‎（第14题图）‎ O y A x B C D N P M G ‎ 又解：求直线CD的解析式为，直线AB的解析式为．‎ ‎ 因为两直线的斜率相等，在y轴上的截距不等，所以两直线平行．（酌情给分）‎ ‎ ‎ ‎（2）①∵PN∥DB ‎ ∴当DE1＝BC时，四边形BCE1D是等腰梯形 ‎ 此时Rt△CNB≌△Rt△E1PD，‎ ‎ ∴PE1＝CN＝2，‎ ‎ ∴点E1（4，3）‎ ‎ ②∵CD∥AB，‎ ‎ 当E2在直线AB上，DE2＝BC＝2，‎ ‎ 四边形BCDE2为等腰梯形，‎ ‎ 直线AB的解析式为 ‎ ‎ ‎∴设点E2（x，）‎ DE2=BC=，‎ ‎∴‎ ‎，（舍去）‎ ‎∴E2（，）； ‎ ‎15.（2016·湖南省岳阳市十二校联考·一模）数学活动：擦出智慧的火花﹣﹣﹣由特殊到一般的数学思想．‎ 数学课上，李老师出示了问题：如图1，四边形ABCD是正方形，点E是边BC上的点，过点E作EF⊥AE，过点F作FG⊥BC交BC的延长线于点G．．‎ ‎（1）求证：∠BAE=∠FEG．‎ ‎（2）同学们很快做出了解答，之后李老师将题目修改成：如图2，四边形ABCD是正方形，点E是边BC的中点．∠AEF=90°，且EF交正方形外角∠DCG的平分线于点F，求证：AE=EF．‎ 经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证△AME≌△ECF，所以AE=EF．请借助图1完成小明的证明；‎ 在（2）的基础上，同学们作了进一步的研究：‎ ‎（3）小聪提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小聪的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．‎ ‎【考点】四边形综合题．‎ ‎【分析】（1）根据∠AEF=90°，即可得到∠AEB+∠FEG=90°，在直角△ABE中，利用三角形内角和定理得到∠BAE+∠AEB=90°，然后根据同角的余角相等，即可证得；‎ ‎（2）作AB的中点M，连接ME，根据ASA即可证明△AME≌△ECF，然后根据全等三角形的对应边相等即可证得；‎ ‎（3）在AB上取一点M，使AM=EC，连接ME，同（2）根据ASA即可证明△AME≌△ECF，然后根据全等三角形的对应边相等即可证得．‎ ‎【解答】解：（1）∵∠AEF=90°，‎ ‎∴∠AEB+∠FEG=90°，‎ 又∵直角△ABE中，∠BAE+∠AEB=90°，‎ ‎∴∠BAE=∠FEG；‎ ‎（2）作AB的中点M，连接ME．‎ ‎∵正方形ABCD中，AB=BC，‎ 又∵AM=MB=AB，BE=CE=BC，‎ ‎∴MB=BE，‎ ‎∴△ABE是等腰直角三角形，‎ ‎∴∠BME=45°，‎ ‎∴∠AME=135°，‎ 又∵∠ECF=180°﹣∠FCG=180°﹣45°=135°．‎ ‎∴∠AME=∠ECF，‎ ‎∴在△AME和△ECF中，‎ ‎，‎ ‎∴△AME≌△ECF，‎ ‎∴AE=EF；‎ ‎（3）在AB上取一点M，使AM=EC，连接ME．‎ ‎∴BM=BE，‎ ‎∴∠BME=45°，‎ ‎∴∠AME=135°，‎ ‎∵CF是外角平分线，‎ ‎∴∠DCF=45°，‎ ‎∴∠ECF=135°‎ ‎∴∠AME=∠ECF ‎∵∠AEB+∠BAE=90°，∠AEB+∠CEF=90°‎ ‎∴∠BAE=∠CEF ‎∴在△AME和△ECF中，‎ ‎，‎ ‎∴△AME≌△ECF（ASA），‎ ‎∴AE=EF．‎ ‎【点评】本题考查了正方形的性质和全等三角形的判定与性质，要注意题目之间的联系，正确作出辅助线构造全等的三角形是本题的关键．‎ ‎16.（2016·黑龙江大庆·一模）如图，在□ABCD中，E、F分别是边AB、CD的中点，BG∥AC交DA的延长线于点G．‎ ‎（1）求证：△ADF≌△CBE；‎ ‎（2）若四边形AGBC是矩形，判断四边形AECF是什么特殊的四边形？并证明你的结论．‎ 答案：（1）证明：∵□ABCD，∴AD=CB，∠D=∠ABC，AB=CD，‎ 又∵E、F分别是边AB、CD的中点，∴DF=BE，∴△ADF∽≌△CBE； ‎ （2） 四边形AECF为菱形；∵矩形AGBC，∴∠ACB=90°，又∵E为AB中点，‎ （3） ‎∴CE=AB=AE，同理AF=FC，∴AF=FC=CE=EA，∴四边形AECF为菱形． ‎ ‎17.（2016·黑龙江齐齐哈尔·一模）如图，矩形ABCD中，AD=5，AB=3，在BC边上取一点E，使BE=4，连结AE，沿AE剪下△ABE，将它平移至△DCF的位置，拼成四边形AEFD．‎ ‎（1）求证:四边形AEFD是菱形；‎ ‎（2）求四边形AEFD的两条对角线的长. ‎ 答案：（1）证明：∵△ABE平移至△DCF的位置.‎ ‎∴△ABE≌△DCF.‎ ‎∴BE=CF ‎∵四边形ABCD为矩形.‎ ‎∴AD∥BC，AD=BC，∠B=90°.‎ ‎∴EF=EC+CF=EC+BE=BC=AD.‎ ‎∴四边形AEFD为平行四边形.‎ 在Rt△ABE中，根据勾股定理得：‎ AE=‎ ‎∵AD=5, ‎ ‎∴AD=AE.‎ ‎∴四边形AEFD为菱形.‎ ‎（2）连结DE、AF.‎ 求出DE=.‎ ‎ 求出AF=.‎ ‎18.（2016·湖北襄阳·一模） (本题11分）如图，在正方形ABCD中，AB=5，P是BC边上任意一点，E是BC延长 线上一点，连接AP，作PF⊥AP，使PF＝PA，连接CF，AF，AF交CD边于点G，连接PG．‎ ‎（1）求证：∠GCF＝∠FCE；‎ ‎（2）判断线段PG，PB与DG之间的数量关系，并证明你的结论；‎ ‎（3）若BP＝2，在直线AB上是否存在一点M，使四　‎ ‎　　边形DMPF是平行四边形，若存在，求出BM的 ‎　　长度，若不存在，说明理由．‎ H K M ‎ ‎ 答案：（1）证明：过点F作FH⊥BE于点H，‎ ‎ ∵四边形ABCD是正方形，‎ ‎ ∴∠ABC＝∠PHF＝∠DCB＝90º,AB＝BC，‎ ‎ ∴∠BAP＋∠APB＝90º ‎ ∵AP⊥PF,‎ ‎ ∴∠APB＋∠FPH＝90º ‎ ∴∠FPH＝∠BAP ‎ ‎ 又∵AP＝PF ‎ ∴△BAP≌△HPF ‎ ‎ ∴PH＝AB，BP＝FH ‎ ‎ ∴PH＝BC ‎ ‎ ∴BP＋PC＝PC＋CH ‎ ∴CH＝BP＝FH ‎ ‎ 而∠FHC＝90º. ∴∠FCH＝CFH＝45º ‎ ∴∠DCF＝90º－45º＝45º ‎ ∴∠GCF＝∠FCE ‎ ‎ （2）PG＝PB＋DG ‎ ‎ 证明：延长PB至K，使BK=DG,‎ ‎ ∵四边形ABCD是正方形 ‎ ∴AB=AD, ∠ABK＝ADG=90º ‎ ∴△ABK≌△ADG ‎ ‎ ∴AK=AG, ∠KAB＝∠GAD,‎ ‎ 而∠APF=90 º,AP=PF ‎ ∴∠PAF＝∠PFA＝45 º ‎ ∴∠BAP＋∠KAB＝∠KAP＝45 º＝∠PAF ‎ ∴△KAP≌△GAP ‎ ‎ ∴KP=PG,‎ ‎ ∴KB＋BP=DG＋BP＝PG ‎ 即，PG＝PB＋DG； ‎ ‎ （3）存在.‎ ‎ 如图，在直线AB上取一点M，使四边形DMPF是平行四边形，‎ ‎ 则MD∥PF，且MD＝FP，‎ ‎ 又∵PF=AP，‎ ‎ ∴MD=AP ‎ ∵四边形ABCD是正方形，‎ ‎ ∴AB=AD，∠ABP=∠DAM ‎ ∴△ABP≌△DAM ‎ ‎ ∴AM＝BP=2，‎ ‎ ∴BM＝AB－AM=5－2=3. ‎ ‎ ∴当BM=3，BM+AM=AB时，四边形DMPF是平行四边形．‎ ‎19.（2016·广东·一模）（本题满分10分）定义：数学活动课上，乐老师给出如下定义：有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形．‎ 理解：（1）如图1，已知A、B、C在格点（小正方形的顶点）上，请在方格图中画出以格点为顶点，AB、BC为边的两个对等四边形ABCD；‎ ‎（2）如图2，在圆内接四边形ABCD中，AB是⊙O的直径，AC=BD．求证：四边形ABCD是对等四边形；‎ ‎（3）如图3，在Rt△PBC中，∠PCB=90°，BC=11，tan∠PBC=，点A在BP边上，且AB=13．用圆规在PC上找到符合条件的点D，使四边形ABCD为对等四边形，并求出CD的长．‎ 解：（1）如图1所示（画2个即可）．‎ ‎ ‎ ‎（2）如图2，连接AC，BD，∵AB是⊙O的直径，∴∠ADB=∠ACB=90°，‎ 在Rt△ADB和Rt△ACB中，‎ ‎ ∴Rt△ADB≌Rt△ACB，∴AD=BC，‎ 又∵AB是⊙O的直径，∴AB≠CD，∴四边形ABCD是对等四边形．‎ ‎（3）如图3，点D的位置如图所示：‎ ‎①若CD=AB，此时点D在D1的位置，CD1=AB=13；‎ ‎②若AD=BC=11，此时点D在D2、D3的位置，AD2=AD3=BC=11，‎ 过点A分别作AE⊥BC，AF⊥PC，垂足为E，F，‎ 设BE=x，∵tan∠PBC=，∴AE=，‎ 在Rt△ABE中，AE2+BE2=AB2，即，解得：x1=5，x2﹣5（舍去），‎ ‎∴BE=5，AE=12，∴CE=BC﹣BE=6，‎ 由四边形AECF为矩形，可得AF=CE=6，CF=AE=12，在Rt△AFD2中，，∴，，‎ 综上所述，CD的长度为13、12﹣或12+．‎ ‎20.（2016·广东东莞·联考）在由m×n（m×n＞1）个小正方形组成的矩形网格中，研究它的一条对角线所穿过的小正方形个数f，‎ ‎（1）当m、n互质（m、n除1外无其他公因数）时，观察下列图形并完成下表：‎ m n m+n f ‎1‎ ‎2‎ ‎3‎ ‎2‎ ‎1‎ ‎3‎ ‎4‎ ‎3‎ ‎2‎ ‎3‎ ‎5‎ ‎4‎ ‎2‎ ‎5‎ ‎7‎ ‎3‎ ‎4‎ ‎7‎ 猜想：当m、n互质时，在m×n的矩形网格中，一条对角线所穿过的小正方形的个数f与m、n的关系式是　f=m+n﹣1　（不需要证明）；‎ ‎（2）当m、n不互质时，请画图验证你猜想的关系式是否依然成立．‎ ‎【考点】作图—应用与设计作图；规律型：图形的变化类．‎ ‎【分析】（1）通过观察即可得出当m、n互质时，在m×n的矩形网格中，一条对角线所穿过的小正方形的个数f与m、n的关系式，‎ ‎（2）当m、n不互质时，画出图即可验证猜想的关系式不成立．‎ ‎【解答】解：（1）表格中分别填6，6‎ m n m+n f ‎1‎ ‎2‎ ‎3‎ ‎2‎ ‎1‎ ‎3‎ ‎4‎ ‎3‎ ‎2‎ ‎3‎ ‎5‎ ‎4‎ ‎2‎ ‎5‎ ‎7‎ ‎6‎ ‎3‎ ‎4‎ ‎7‎ ‎6‎ f与m、n的关系式是：f=m+n﹣1．‎ 故答案为：f=m+n﹣1．‎ ‎（2）m、n不互质时，猜想的关系式不一定成立，如下图：‎ ‎．‎ ‎【点评】此题考查了作图﹣应用与设计作图，关键是通过观察表格，总结出一条对角线所穿过的小正方形的个数f与m、n的关系式，要注意m、n互质的条件．‎ ‎21.（2016·广东东莞·联考）如图，△OBD中，OD=BD，△OBD绕点O逆时针旋转一定角度后得到△OAC，此时B，D，C三点正好在一条直线上，且点D是BC的中点．‎ ‎（1）求∠COD度数；‎ ‎（2）求证：四边形ODAC是菱形．‎ ‎【考点】旋转的性质；菱形的判定．‎ ‎【分析】（1）如图，根据题意证明△OBC为直角三角形，结合OC=，求出∠B即可解决问题．‎ ‎（2）首先证明AC∥OD，结合AC=OD，判断四边形ADOC为平行四边形，根据菱形的定义即可解决问题．‎ ‎【解答】解：（1）如图，由题意得：OC=OD=BD；‎ ‎∵点D是BC的中点，‎ ‎∴CD=BD，OD=BC，‎ ‎∴△OBC为直角三角形，而OC=，‎ ‎∴∠B=30°，∠OCD=90°﹣30°=60°，；‎ ‎∵OD=CD，‎ ‎∴∠COD=∠OCD=60°．‎ ‎（2）∵OD=BD，‎ ‎∴∠DOB=∠B=30°，‎ 由旋转变换的性质知：‎ ‎∠COA=∠CAO=∠B=30°，‎ ‎∴∠AOD=90°﹣2×30°=30°，‎ ‎∴∠CAO=∠AOD=30°，‎ ‎∴AC∥OD，而AC=OD，‎ ‎∴四边形ADOC为平行四边形，而OC=OD，‎ ‎∴四边形ODAC是菱形．‎ ‎【点评】该题主要考查了旋转变换的性质、直角三角形的判定、菱形的判定等几何知识点及其应用问题；解题的关键是牢固掌握旋转变换的性质、直角三角形的判定、菱形的判定等几何知识点，并能灵活运用．‎ ‎22.（2016·广东东莞·联考）如图1，将菱形纸片AB（E）CD（F）沿对角线BD（EF）剪开，得到△ABD和△ECF，固定△ABD，并把△ABD与△ECF 叠放在一起．‎ ‎（1）操作：如图2，将△ECF的顶点F固定在△ABD的BD边上的中点处，△ECF绕点F在BD边上方左右旋转，设旋转时FC交BA于点H（H点不与B点重合），FE交DA于点G（G点不与D点重合）．‎ 求证：BH•GD=BF2‎ ‎（2）操作：如图3，△ECF的顶点F在△ABD的BD边上滑动（F点不与B、D点重合），且CF始终经过点A，过点A作AG∥CE，交FE于点G，连接DG．‎ 探究：FD+DG=　DB　．请予证明．‎ ‎【考点】相似三角形的判定与性质；全等三角形的判定与性质；菱形的性质；旋转的性质．‎ ‎【专题】压轴题．‎ ‎【分析】（1）根据菱形的性质以及相似三角形的判定得出△BFH∽△DGF，即可得出答案；‎ ‎（2）利用已知以及平行线的性质证明△ABF≌△ADG，即可得出FD+DG的关系．‎ ‎【解答】证明：（1）∵将菱形纸片AB（E）CD（F）沿对角线BD（EF）剪开，‎ ‎∴∠B=∠D，‎ ‎∵将△ECF的顶点F固定在△ABD的BD边上的中点处，△ECF绕点F在BD边上方左右旋转，‎ ‎∴BF=DF，‎ ‎∵∠HFG=∠B，‎ 又∵∠HFD=∠HFG+∠GFD=∠B+∠BHF ‎∴∠GFD=∠BHF，‎ ‎∴△BFH∽△DGF，‎ ‎∴，‎ ‎∴BH•GD=BF2；‎ ‎（2）∵AG∥CE，‎ ‎∴∠FAG=∠C，‎ ‎∵∠CFE=∠CEF，‎ ‎∴∠AGF=∠CFE，‎ ‎∴AF=AG，‎ ‎∵∠BAD=∠C，‎ ‎∴∠BAF=∠DAG，‎ 又∵AB=AD，‎ ‎∴△ABF≌△ADG，‎ ‎∴FB=DG，‎ ‎∴FD+DG=BD，‎ 故答案为：BD．‎ ‎【点评】此题主要考查了相似三角形的判定以及全等三角形的判定，根据等腰三角形的性质得出∠BAF=∠DAG是解决问题的关键．‎ ‎23.（2016·广东河源·一模）已知一张矩形纸片OACB，将该纸片放置在平面直角坐标系中，点A（11，0），B（0，6），点P为BC边上的动点（点P不与点B，C重合），经过点O、P折叠该纸片，得点B′和折痕OP．设BP＝t 。‎ ‎（1）如图①，当∠BOP＝30°时，求点P的坐标；‎ ‎（2）如图②，经过点P再次折叠纸片，使点C 落在直线PB′上，得点C′‎ 和折痕PQ，若AQ＝m，试用含有t的式子表示m； ‎ ‎（3）在（2）的条件下，当点C′恰好落在边OA上时，求点P的坐标。（直接写出结果即可）‎ 解：（1）根据题意，有∠OBP = 90°，OB = 6，‎ 在Rt△OBP中，由∠BOP = 30°，BP =t，得OP＝2t.‎ ‎∵OP 2 ＝ OB 2+BP 2，即（2t）2 ＝62+t 2，解得t1＝，t2＝－（舍去）．‎ ‎∴点P的坐标为（ ，6）．‎ ‎（2）∵△OB′P，△QC′P分别是由△OBP，△QCP折叠得到的，‎ ‎∴△OB′P ≌ △OBP，△QC′P ≌ △QCP.‎ ‎∴∠OPB′＝∠OPB，∠QPC′＝∠QPC.‎ ‎∵∠OPB′+∠OPB +∠QPC′+∠QPC＝180°，∴∠OPB +∠QPC＝90°.‎ ‎∵∠BOP +∠OPB＝90°，∴∠BOP＝∠CPQ.‎ 又∵∠OBP＝∠C = 90°，∴△OBP∽△PCQ.∴.‎ 由题意知，BP＝t，AQ＝m，BC＝11，AC＝6，则PC＝11－t，CQ＝6－m．‎ ‎∴∴（0＜t＜11）.‎ （3） 点P的坐标为（，6）或（，6）.‎ ‎24.（2016·河南三门峡·一模）（10分）如图，在平行四边形ABCD中，AB≠BC，连接AC，AE是∠BAD的平分线，交边DC的延长线于点F．‎ ‎（1）证明：CE=CF；‎ ‎（2）若∠B=60°，BC=2AB，试判断四边形ABFC的形状，并说明理由．（如图2所示）‎ 解：（1）证明：如图（1），‎ ‎∵AE是∠BAD的平分线，‎ ‎∴∠BAF=∠DAF，‎ 在平行四边形ABCD中，‎ ‎∵AB∥DF，AD∥BC，‎ ‎∴∠BAF=∠F，∠DAF=∠CEF，‎ ‎∴∠F=∠CEF，‎ ‎∴CE=CF；‎ ‎（2）解：四边形ABFC是矩形，‎ 理由：如图（2），∵∠ABC=60°，AD∥BC，‎ ‎∴∠BAD=120°，‎ ‎∵∠BAF=∠DAF，‎ ‎∴∠BAF=60°，‎ 则△ABE是等边三角形，‎ 可得AB=BE=AE，∠BEA=∠CEF=∠AFC=60°，‎ ‎∵BC=2AB，‎ ‎∴AE=BE=EC，‎ ‎∴△ABC是直角三角形，∠BAC=90°，‎ 在△ABE和△FCE中 ‎∵，‎ ‎∴△ABE≌△FCE（ASA），‎ ‎∴AB=FC，‎ 又∵AB∥FC，‎ ‎∴四边形ABFC是平行四边形，‎ 再由∠BAC=90°，‎ 故四边形ABFC是矩形．‎