上海历年中考数学压轴题复习试题附答案 20页

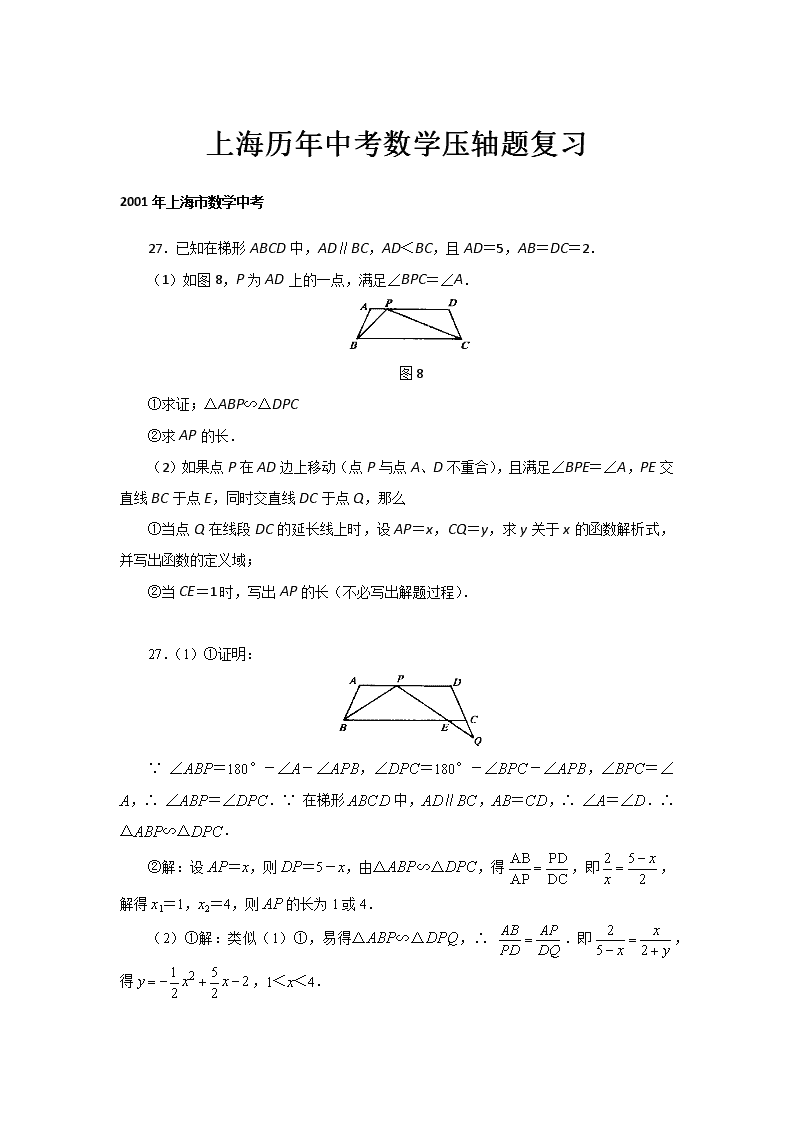
上海历年中考数学压轴题复习 ‎2001年上海市数学中考 ‎27．已知在梯形ABCD中，AD∥BC，AD＜BC，且AD＝5，AB＝DC＝2．‎ ‎（1）如图8，P为AD上的一点，满足∠BPC＝∠A．‎ 图8‎ ‎①求证；△ABP∽△DPC ‎②求AP的长．‎ ‎（2）如果点P在AD边上移动（点P与点A、D不重合），且满足∠BPE＝∠A，PE交直线BC于点E，同时交直线DC于点Q，那么 ‎①当点Q在线段DC的延长线上时，设AP＝x，CQ＝y，求y关于x的函数解析式，并写出函数的定义域；‎ ‎②当CE＝1时，写出AP的长（不必写出解题过程）．‎ ‎27．（1）①证明：‎ ‎∵ ∠ABP＝180°－∠A－∠APB，∠DPC＝180°－∠BPC－∠APB，∠BPC＝∠A，∴ ∠ABP＝∠DPC．∵ 在梯形ABCD中，AD∥BC，AB＝CD，∴ ∠A＝∠D．∴ △ABP∽△DPC．‎ ‎②解：设AP＝x，则DP＝5－x，由△ABP∽△DPC，得，即，解得x1＝1，x2＝4，则AP的长为1或4．‎ ‎（2）①解：类似（1）①，易得△ABP∽△DPQ，∴ ．即，得，1＜x＜4．‎ ‎②AP＝2或AP＝3－．‎ ‎（题27是一道涉及动量与变量的考题，其中（1）可看作（2）的特例，故（2）的推断与证明均可借鉴（1）的思路．这是一种从模仿到创造的过程，模仿即借鉴、套用，创造即灵活变化，这是中学生学数学应具备的一种基本素质，世上的万事万物总有着千丝万缕的联系，也有着质的区别，模仿的关键是发现联系，创造的关键是发现区别，并找到应付新问题的途径．）‎ 上海市2002年中等学校高中阶段招生文化考试 ‎　27．操作：将一把三角尺放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于点Q．‎ 图5图6图7‎ ‎　　探究：设A、P两点间的距离为x．‎ ‎　　（1）当点Q在边CD上时，线段PQ与线段PB之间有怎样的大小关系？试证明你观察得到结论；‎ ‎　　（2）当点Q在边CD上时，设四边形PBCQ的面积为y，求y与x之间的函数解析式，并写出函数的定义域；‎ ‎　　（3）当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置，并求出相应的x的值；如果不可能，试说明理由．‎ ‎　　（图5、图6、图7的形状大小相同，图5供操作、实验用，图6和图7备用）‎ 五、（本大题只有1题，满分12分，（1）、（2）、（3）题均为4分）‎ ‎　　27．‎ 图1 图2 图3‎ ‎  （1）解：PQ＝PB　　　　　　　　　　　　　　　　……………………（1分）‎ ‎　　证明如下：过点P作MN∥BC，分别交AB于点M，交CD于点N，那么四边形AMND和四边形BCNM都是矩形，△AMP和△CNP都是等腰直角三角形（如图1）．‎ ‎　　∴　NP＝NC＝MB．　　　　　　　　　　　　　　　　　……………………（1分）‎ ‎　　∵　∠BPQ＝90°，∴　∠QPN＋∠BPM＝90°．‎ ‎　　 而∠BPM＋∠PBM＝90°，∴　∠QPN＝∠PBM．　　　……………………（1分）‎ ‎　　又∵　∠QNP＝∠PMB＝90°，∴　△QNP≌△PMB．　……………………（1分）‎ ‎　　∴　PQ＝PB．‎ ‎　　（2）解法一 ‎　　由（1）△QNP≌△PMB．得NQ＝MP．‎ ‎　　∵　AP＝x，∴　AM＝MP＝NQ＝DN＝，BM＝PN＝CN＝1－，‎ ‎　　∴　CQ＝CD－DQ＝1－2·＝1－．‎ ‎　　得S△PBC＝BC·BM＝×1×（1－）＝－x．　………………（1分）‎ ‎　　S△PCQ＝CQ·PN＝×（1－）（1－）＝－＋x2　　（1分）‎ ‎　　S四边形PBCQ＝S△PBC＋S△PCQ＝x2－＋1．‎ ‎　　即　y＝x2－＋1（0≤x＜）．　　　　　　……………………（1分，1分）‎ ‎　　解法二 ‎　　作PT⊥BC，T为垂足（如图2），那么四边形PTCN为正方形．‎ ‎　　∴　PT＝CB＝PN．‎ ‎　　又∠PNQ＝∠PTB＝90°，PB＝PQ，∴△PBT≌△PQN．‎ ‎　　S四边形PBCQ＝S△四边形PBT＋S四边形PTCQ＝S四边形PTCQ＋S△PQN＝S正方形PTCN　…（2分）‎ ‎　　    ＝CN2＝（1－）2＝x2－＋1‎ ‎　　∴　y＝x2－＋1（0≤x＜）．　　　　　　　　……………………（1分）（3）△PCQ可能成为等腰三角形 ‎　　①当点P与点A重合，点Q与点D重合，这时PQ＝QC，△PCQ是等腰三角形，‎ ‎　　 此时x＝0　　　　　　　　　　　　　　　　　　　　　……………………（1分）‎ ‎　　②当点Q在边DC的延长线上，且CP＝CQ时，△PCQ是等腰三角形（如图3）‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　　　……………………（1分）‎ ‎　　解法一　此时，QN＝PM＝，CP＝－x，CN＝CP＝1－．‎ ‎　　∴ CQ＝QN－CN＝－（1－）＝－1．‎ ‎　　当－x＝－1时，得x＝1．　　　　　　　　　　　……………………（1分）‎ ‎　　解法二　此时∠CPQ＝∠PCN＝22.5°，∠APB＝90°－22.5°＝67.5°，‎ ‎　　∠ABP＝180°－（45°＋67.5°）＝67.5°，得∠APB＝∠ABP，‎ ‎　　∴　AP＝AB＝1，∴　x＝1．　　　　　　　　　　　　　……………………（1分）‎ 上海市2003年初中毕业高中招生统一考试 ‎27.如图，在正方形ABCD中，AB＝1，弧AC是点B为圆心，AB长为半径的圆的一段弧。点E是边AD上的任意一点（点E与点A、D不重合），过E作弧AC所在圆的切线，交边DC于点F，G为切点： （1）当∠DEF＝45º时，求证：点G为线段EF的中点；‎ ‎（2）设AE＝x，FC＝y，求y关于x的函数解析式，并写出函数的定义域；‎ ‎（3）将△DEF沿直线EF翻折后得△DEF，如图，当EF＝时，讨论△ADD与△EDF是否相似，如果相似，请加以证明；如果不相似，只要求写出结论，不要求写出理由。‎ ‎ ‎ ‎2004年上海市中考数学试卷 ‎27、（2004•上海）数学课上，老师提出：‎ 如图，在平面直角坐标系中，O为坐标原点，A点的坐标为（1，0），点B在x轴上，且在点A的右侧，AB=OA，过点A和B作x轴的垂线，分别交二次函数y=x2的图象于点C和D，直线OC交BD于点M，直线CD交y轴于点H，记点C、D的的横坐标分别为xC、xD，点H的纵坐标为yH．‎ 同学发现两个结论：‎ ‎①S△CMD：S梯形ABMC=2：3 ②数值相等关系：xC•xD=﹣yH ‎（1）请你验证结论①和结论②成立；‎ ‎（2）请你研究：如果上述框中的条件“A的坐标（1，0）”改为“A的坐标（t，0）（t＞0）”，其他条件不变，结论①是否仍成立（请说明理由）；‎ ‎（3）进一步研究：如果上述框中的条件“A的坐标（1，0）”改为“A的坐标（t，0）（t＞0）”，又将条件“y=x‎2”‎改为“y=ax2（a＞0）”，其他条件不变，那么xC、xD与yH有怎样的数值关系？（写出结果并说明理由）‎ 考点：二次函数综合题。‎ 专题：压轴题。‎ 分析：（1）可先根据AB=OA得出B点的坐标，然后根据抛物线的解析式和A，B的坐标得出C，D两点的坐标，再依据C点的坐标求出直线OC的解析式．进而可求出M点的坐标，然后根据C、D两点的坐标求出直线CD的解析式进而求出D点的坐标，然后可根据这些点的坐标进行求解即可；‎ ‎（2）（3）的解法同（1）完全一样．‎ 解答：解：（1）由已知可得点B的坐标为（2，0），点C坐标为（1，1），点D 的坐标为（2，4），‎ 由点C坐标为（1，1）易得直线OC的函数解析式为y=x，‎ 故点M的坐标为（2，2），‎ 所以S△CMD=1，S梯形ABMC=‎‎3‎‎2‎ 所以S△CMD：S梯形ABMC=2：3，‎ 即结论①成立．‎ 设直线CD的函数解析式为y=kx+b，‎ 则‎&k+b=1‎‎&2k+b=4‎，‎ 解得‎&k=3‎‎&b=﹣2‎ 所以直线CD的函数解析式为y=3x﹣2．‎ 由上述可得，点H的坐标为（0，﹣2），yH=﹣2‎ 因为xC•xD=2，‎ 所以xC•xD=﹣yH，‎ 即结论②成立；‎ ‎（2）（1）的结论仍然成立．‎ 理由：当A的坐标（t，0）（t＞0）时，点B的坐标为（2t，0），点C坐标为（t，t2），点D的坐标为（2t，4t2），‎ 由点C坐标为（t，t2）易得直线OC的函数解析式为y=tx，‎ 故点M的坐标为（2t，2t2），‎ 所以S△CMD=t3，S梯形ABMC=‎3‎‎2‎t3．‎ 所以S△CMD：S梯形ABMC=2：3，‎ 即结论①成立．‎ 设直线CD的函数解析式为y=kx+b，‎ 则‎&tk+b=‎t‎2‎‎&2tk+b=4‎t‎2‎，‎ 解得‎&k=3t‎&b=﹣2‎t‎2‎ 所以直线CD的函数解析式为y=3tx﹣2t2；‎ 由上述可得，点H的坐标为（0，﹣2t2），yH=﹣2t2‎ 因为xC•xD=2t2，‎ 所以xC•xD=﹣yH，‎ 即结论②成立；‎ ‎（3）由题意，当二次函数的解析式为y=ax2（a＞0），且点A坐标为（t，0）（t＞0）时，点C坐标为（t，at2），点D坐标为（2t，4at2），‎ 设直线CD的解析式为y=kx+b，‎ 则：‎&tk+b=at‎2‎‎&2tk+b=4at‎2‎，‎ 解得‎&k=3at‎&b=﹣2at‎2‎ 所以直线CD的函数解析式为y=3atx﹣2at2，则点H的坐标为（0，﹣2at2），yH=﹣2at2．‎ 因为xC•xD=2t2，‎ 所以xC•xD=﹣‎1‎ayH．‎ 点评：本题主要考查了二次函数的应用、一次函数解析式的确定、图形面积的求法、函数图象的交点等知识点．‎ ‎2005年上海市初中毕业生统一学业考试数学试卷 1、 ‎（本题满分12分，每小题满分各为4分）‎ 在△ABC中，∠ABC＝90°，AB＝4，BC＝3，O是边AC上的一个动点，以点O为圆心作半圆，与边AB相切于点D，交线段OC于点E，作EP⊥ED，交射线AB于点P，交射线CB于点F。‎ （1） 如图8，求证：△ADE∽△AEP；‎ （2） 设OA＝x，AP＝y，求y关于x的函数解析式，并写出它的定义域；‎ （3） 当BF＝1时，求线段AP的长.‎ J 2006 年上海市初中毕业生统一学业考试数学试卷 ‎25（本题满分14分，第（1）小题满分4分，第（2）小题满分7分，第（3）小题满分3分）‎ 已知点P在线段AB上，点O在线段AB的延长线上。以点O为圆心，OP为半径作圆，点C是圆O上的一点。‎ （1） 如图9，如果AP=2PB，PB=BO。求证：△CAO∽△BCO；‎ （2） 如果AP=m（m是常数，且m〉1），BP=1，OP是OA、OB的比例中项。当点C在圆O上运动时，求AC：BC的值（结果用含m的式子表示）；‎ （3） 在（2）的条件下，讨论以BC为半径的圆B和以CA为半径的圆C的位置关系，并写出相应m的取值范围。‎ 图9‎ A P B O C ‎25．（1）证明：，．‎ ‎． （2分）‎ ‎， （1分）‎ ‎．，． （1分）‎ ‎（2）解：设，则，，是，的比例中项，‎ ‎， （1分）‎ 得，即． （1分）‎ ‎． （1分）‎ 是，的比例中项，即，‎ ‎，． （1分）‎ 设圆与线段的延长线相交于点，当点与点，点不重合时，‎ ‎，． （1分）‎ ‎． （1分）‎ ‎；当点与点或点重合时，可得，‎ 当点在圆上运动时，； （1分）‎ ‎（3）解：由（2）得，，且，‎ ‎，圆和圆的圆心距，‎ 显然，圆和圆的位置关系只可能相交、内切或内含．‎ 当圆与圆相交时，，得，‎ ‎，； （1分）‎ 当圆与圆内切时，，得； （1分）‎ 当圆与圆内含时，，得． （1分）‎ ‎2007年上海市初中毕业生统一学业考试 ‎25．（本题满分14分，第（1）小题满分4分，第（2），（3）小题满分各5分）‎ 已知：，点在射线上，（如图10）．为直线上一动点，以为边作等边三角形（点按顺时针排列），是的外心．‎ ‎（1）当点在射线上运动时，求证：点在的平分线上；‎ ‎（2）当点在射线上运动（点与点不重合）时，与交于点，设，，求关于的函数解析式，并写出函数的定义域；‎ ‎（3）若点在射线上，，圆为的内切圆．当的边或与圆相切时，请直接写出点与点的距离．‎ 图10‎ 备用图 ‎25．（1）证明：如图4，连结，‎ 是等边三角形的外心，， 1分 圆心角．‎ 当不垂直于时，作，，垂足分别为．‎ 由，且，‎ ‎，．‎ ‎． 1分 ‎． 1分 ‎．点在的平分线上． 1分 当时，．‎ 即，点在的平分线上．‎ 综上所述，当点在射线上运动时，点在的平分线上．‎ 图4‎ 图5‎ ‎（2）解：如图5，‎ 平分，且，‎ ‎． 1分 由（1）知，，，‎ ‎，．‎ ‎，． 1分 ‎．‎ ‎．．． 1分 定义域为：． 1分 ‎（3）解：①如图6，当与圆相切时，； 2分 ‎②如图7，当与圆相切时，； 1分 ‎③如图8，当与圆相切时，． 2分 图6‎ 图7‎ 图8‎ ‎2008年上海市中考数学试卷 ‎25．（本题满分14分，第（1）小题满分5分，第（2）小题满分4分，第（3）小题满分5分）‎ 已知，，（如图13）．是射线上的动点（点与点不重合），是线段的中点．‎ ‎（1）设，的面积为，求关于的函数解析式，并写出函数的定义域；‎ ‎（2）如果以线段为直径的圆与以线段为直径的圆外切，求线段的长；‎ ‎（3）联结，交线段于点，如果以为顶点的三角形与相似，求线段的长．‎ B A D M E C 图13‎ B A D C 备用图 ‎25．解：（1）取中点，联结，‎ 为的中点，，． （1分）‎ 又，． （1分）‎ ‎，得； （2分）（1分）‎ ‎（2）由已知得． （1分）‎ 以线段为直径的圆与以线段为直径的圆外切，‎ ‎，即． （2分）‎ 解得，即线段的长为； （1分）‎ ‎（3）由已知，以为顶点的三角形与相似，‎ 又易证得． （1分）‎ 由此可知，另一对对应角相等有两种情况：①；②．‎ ‎①当时，，．．‎ ‎，易得．得； （2分）‎ ‎②当时，，．‎ ‎．又，．‎ ‎，即，得．‎ 解得，（舍去）．即线段的长为2． （2分）‎ 综上所述，所求线段的长为8或2．‎ ‎2009年上海市初中毕业统一学业考试 ‎25．（本题满分14分，第（1）小题满分4分，第（2）小题满分5分，第（3）小题满分5分）‎ 已知为线段上的动点，点在射线上，且满足（如图8所示）．‎ ‎（1）当，且点与点重合时（如图9所示），求线段的长；‎ ‎（2）在图8中，联结．当，且点在线段上时，设点之间的距离 为，，其中表示的面积，表示的面积，求关于的函数解析式，并写出函数定义域；‎ A D P C B Q 图8‎ D A P C B ‎（Q）‎ ‎）‎ 图9‎ 图10‎ C A D P B Q ‎（3）当，且点在线段的延长线上时（如图10所示），求的大小．‎ ‎（2009年上海25题解析） 解：（1）AD=2，且Q点与B点重合，根据题意，∠PBC=∠PDA，因为∠A=90。 PQ/PC=AD/AB=1,所以：△PQC为等腰直角三角形，BC=3，所以：PC=3 /2,‎ ‎（2）如图：添加辅助线，根据题意，两个三角形的面积可以分别表示成S1，S2， 高分别是H，h，‎ 则：S1=（2-x）H/2=（2*3/2）/2-(x*H/2)-(3/2)*(2-h)/2‎ S2=3*h/2 因为两S1/S2=y，消去H,h,得：‎ Y=-(1/4)*x+(1/2), ‎ 定义域：当点P运动到与D点重合时，X的取值就是最大值，当PC垂直BD时，这时X=0，连接DC,作QD垂直DC，由已知条件得：B、Q、D、C四点共圆，则由圆周角定理可以推知：三角形QDC相似于三角形ABD QD/DC=AD/AB=3/4，令QD=3t,DC=4t,则：QC=5t，由勾股定理得：‎ 直角三角形AQD中：(3/2)^2+(2-x)^2=(3t)^2‎ 直角三角形QBC中：3^2+x^2=(5t)^2‎ 整理得：64x^2-400x+301=0 (8x-7)(8x-43)=0‎ ‎ 得 x1=7/8 x2=(43/8)>2(舍去) 所以函数:‎ Y=-(1/4)*x+1/2的定义域为[0，7/8]‎ ‎(3)因为：PQ/PC=AD/AB,假设PQ不垂直PC，则可以作一条直线PQ′垂直于PC，与AB交于Q′点，‎ 则：B，Q′，P，C四点共圆，由圆周角定理，以及相似三角形的性质得：‎ PQ′/PC=AD/AB,‎ 又由于PQ/PC=AD/AB 所以，点Q′与点Q重合，所以角∠QPC=90。 ‎ A D P C B Q 图8‎ D A P C B ‎（Q）‎ ‎）‎ 图9‎ 图10‎ C A D P B Q ‎2010年上海市初中毕业统一学业考试数学卷 ‎25．如图9，在Rt△ABC中，∠ACB＝90°.半径为1的圆A与边AB相交于点D，与边AC相交于点E，连结DE并延长，与线段BC的延长线交于点P.‎ ‎（1）当∠B＝30°时，连结AP，若△AEP与△BDP相似，求CE的长；‎ ‎（2）若CE=2，BD=BC，求∠BPD的正切值；‎ ‎（3）若，设CE=x，△ABC的周长为y，求y关于x的函数关系式.‎ 图9 图10(备用) 图11(备用)‎ ‎2011年上海市初中毕业统一学业考试数学卷 ‎2011年上海市初中毕业统一学业考试数学卷 ‎25．（本题满分14分，第（1）小题满分4分，第（2）、（3）小题满分各5分）‎ 在Rt△ABC中，∠ACB＝90°，BC＝30，AB＝50．点P是AB边上任意一点，直线PE⊥AB，与边AC或BC相交于E．点M在线段AP上，点N在线段BP上，EM＝EN，．‎ ‎（1）如图1，当点E与点C重合时，求CM的长；‎ ‎（2）如图2，当点E在边AC上时，点E不与点A、C重合，设AP＝x，BN＝y，求y关于x的函数关系式，并写出函数的定义域；‎ ‎（3）若△AME∽△ENB（△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应），求AP的长．‎ 图1 图2 备用图 ‎25. (本题满分14分，第(1)小题满分4分，第(2)、(3)小题满分各5分)‎ ‎ [解] (1) 由AE=40，BC=30，AB=50，ÞCP=24，又sinÐEMP=ÞCM=26。‎ ‎ (2) 在Rt△AEP與Rt△ABC中，∵ ÐEAP=ÐBAC，∴ Rt△AEP ~ Rt△ABC，‎ ‎ ∴ ，即，∴ EP=x，‎ ‎ 又sinÐEMP=ÞtgÐEMP==Þ=，∴ MP=x=PN，‎ ‎ BN=AB-AP-PN=50-x-x=50-x (0