2017平谷中考数学一模试卷与答案 12页

平谷区2017年初三统一练习（一）‎ ‎ 2017.4‎ 一、选择题(本题共30分，每小题3分)‎ ‎1．为解决“最后一公里”的交通接驳问题，平谷区投放了大量公租自行车供市民使用．据统计，目前我区共有公租自行车3 500辆．将3 500用科学记数法表示应为 ‎　 A．0.35×104 B． 3.5×103 C．3.5×102 D． 35×102‎ ‎2．把一个边长为1的正方形如图所示放在数轴上，以正方形的对角线为半径画弧交数轴于点A，则点A对应的数是 A．1 B． C． D．2‎ ‎3．右图是某几何体从不同角度看到的图形，这个几何体是 主视图　　 左视图 俯视图 A．圆锥　　　 B．圆柱　　　‎ C．正三棱柱　　 D．三棱锥 ‎4．如果x+y=4，那么代数式的值是 A．﹣2 B．2 C． D．‎ ‎5．下列图形中，既是轴对称图形，又是中心对称图形的是 A． B． C． D．‎ ‎6．某商场一楼与二楼之间的手扶电梯如图所示．其中AB、CD分别表示一楼、二楼地面的水平线，∠ABC=150°，BC的长是8 m，则乘电梯从点B到点C上升的高度h是 A B C D ‎150°‎ h A．m B．8 m C．m D．4 m ‎7．在我国古代数学著作《九章算术》中记载了一道有趣的数学问题：“今有凫（凫：野鸭）起南海，七日至北海；雁起北海，九日至南海.今凫雁俱起，问何日相逢？”意思是：野鸭从南海起飞，7天飞到北海；大雁从北海起飞，9天飞到南海．野鸭与大雁从南海和北海同时起飞，经过几天相遇．设野鸭与大雁从南海和北海同时起飞，经过天相遇，根据题意，下面所列方程正确的是 ‎ A． B. ‎ C. D. 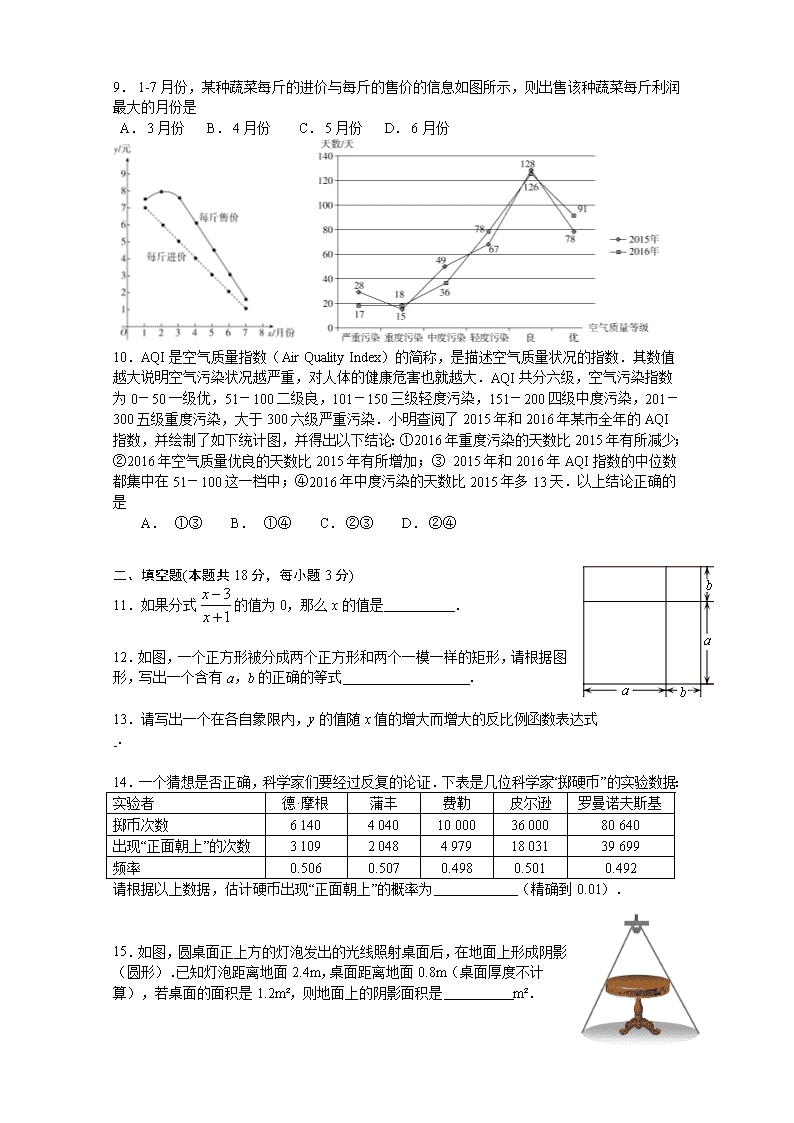‎ ‎8．如图，是利用平面直角坐标系画出的天安门广场的平面示意图，若这个坐标系分别以正东、 正北方向为x轴、y轴的正方向， 表示国旗杆的点的坐标为(0，2.5)， 表示中国国家博物馆的点的坐标为(4，1)， 则表示下列建筑的点的坐标正确的是 A．天安门(0， 4) B．人民大会堂(﹣4，1)‎ C．毛主席纪念堂(﹣1，﹣3) D．正阳门(0，﹣5) ‎ ‎9．1-7月份，某种蔬菜每斤的进价与每斤的售价的信息如图所示，则出售该种蔬菜每斤利润最大的月份是 A．3月份 B．4月份 C．5月份 D．6月份 ‎10．AQI是空气质量指数（Air Quality Index）的简称，是描述空气质量状况的指数．其数值越大说明空气污染状况越严重，对人体的健康危害也就越大．AQI共分六级，空气污染指数为0－50一级优，51－100二级良，101－150三级轻度污染，151－200四级中度污染，201－300五级重度污染，大于300六级严重污染．小明查阅了2015年和2016年某市全年的AQI指数，并绘制了如下统计图，并得出以下结论：①2016年重度污染的天数比2015年有所减少；②2016年空气质量优良的天数比2015年有所增加；③ 2015年和2016年AQI指数的中位数都集中在51－100这一档中；④2016年中度污染的天数比2015年多13天．以上结论正确的是 A． ①③ B． ①④ C．②③ D．②④‎ 二、填空题(本题共18分，每小题3分)‎ ‎11．如果分式的值为0，那么x的值是 ． ‎ ‎12．如图，一个正方形被分成两个正方形和两个一模一样的矩形，请根据图形，写出一个含有a，b的正确的等式 ．‎ ‎13．请写出一个在各自象限内，y的值随x值的增大而增大的反比例函数表达式  ．‎ ‎14．一个猜想是否正确，科学家们要经过反复的论证．下表是几位科学家“掷硬币”的实验数据：‎ 实验者 德·摩根 蒲丰 费勒 皮尔逊 罗曼诺夫斯基 掷币次数 ‎6 140‎ ‎4 040‎ ‎10 000‎ ‎36 000‎ ‎80 640‎ 出现“正面朝上”的次数 ‎3 109‎ ‎2 048‎ ‎4 979‎ ‎18 031‎ ‎39 699‎ 频率 ‎0.506‎ ‎0.507‎ ‎0.498‎ ‎0.501‎ ‎0.492‎ 请根据以上数据，估计硬币出现“正面朝上”的概率为 （精确到0.01）．‎ ‎15．如图，圆桌面正上方的灯泡发出的光线照射桌面后，在地面上形成阴影（圆形）．已知灯泡距离地面2.4m，桌面距离地面0.8m（桌面厚度不计算），若桌面的面积是1.2m²，则地面上的阴影面积是 m²．‎ ‎16．小米是一个爱动脑筋的孩子，他用如下方法作∠AOB的角平分线：‎ ‎ 作法：如图，‎ ‎（1）在射线OA上任取一点C，过点C作CD∥OB；‎ ‎（2）以点C为圆心，CO的长为半径作弧，交CD于点E；‎ ‎（3）作射线OE．‎ 所以射线OE就是∠AOB的角平分线． ‎ 请回答：小米的作图依据是____________________________‎ ‎____________________________________________________．‎ 三、解答题（本题共72分，第17-26题，每小题5分，第27题7分，第28题7分，第29题8分）解答应写出文字说明、演算步骤或证明过程.‎ ‎17．计算：．‎ ‎18．解不等式组并写出它的所有非负整数解．‎ ‎19．如图，在矩形ABCD中，点E是BC上一点，且DE=DA，AF⊥DE于F，求证：AF=CD．‎ ‎20．已知关于x的一元二次方程x2-(m+2)x+2m=0．‎ ‎（1）求证：方程总有两个实数根；‎ ‎（2）当m=2时，求方程的两个根．‎ ‎21．在平面直角坐标xOy中，直线与双曲线的一个交点为A（﹣2，3），与x轴交于点B．‎ ‎(1) 求m的值和点B的坐标；‎ ‎(2) 点P在y轴上，点P到直线的距离为，直接写出点P的坐标．‎ ‎22．随着人们“节能环保，绿色出行”意识的增强，越来越多的人喜欢骑自行车出行．某自行车厂生产的某型号自行车去年销售总额为8万元．今年该型号自行车每辆售价预计比去年降低200元．若该型号车的销售数量与去年相同，那么今年的销售总额将比去年减少10%，求该型号自行车去年每辆售价多少元？‎ ‎23．如图，在△ABC中，BD平分∠ABC交AC于D，EF垂直平分BD，分别交AB，BC，BD于E，F，G，连接DE，DF．‎ ‎（1）求证：DE=DF；‎ ‎（2）若∠ABC=30°，∠C=45°，DE=4，求CF的长．‎ ‎24．阅读以下材料：‎ ‎ 2017年1月28日至2月1日农历正月初一至初五，平谷区政府在占地面积6万平方米的琴湖公园举办主题为“逛平谷庙会乐百姓生活”的平谷区首届春节庙会．‎ ‎ 本次庙会共设置了文艺展演区、非遗展示互动区、特色商品区、儿童娱乐游艺区、特色美食区等五个不同主题的展区．展区总面积1720平方米．文艺展演区占地面积600平方米，占展区总面积的34.9％；非遗展示区占地190平方米，占展区总面积的11.0％；特色商品区占地面积是文艺展演区的一半，占展区总面积的17.4％；特色美食区占地200平方米，占展区总面积的11.6％；还有孩子们喜爱的儿童娱乐游艺区．‎ ‎ 此次庙会本着弘扬、挖掘、展示平谷春节及民俗文化，以京津冀不同地域的特色文化为出发点，全面展示平谷风土人情及津冀人文特色．大年初一，来自全国各地的约3.2万人踏着新春的脚步，揭开了首届平谷庙会的帷幕．大年初二尽管天气寒冷，市民逛庙会热情不减，又约有4.3万人次参观了庙会，品尝特色美食，观看绿都古韵、秧歌表演、天桥绝活，一路猜灯谜、赏图片展，场面火爆．琳琅满目的泥塑、木版画、剪纸、年画等民俗作品也让游客爱不释手，纷纷购买．大年初三，单日接待游客约4万人次，大年初四风和日丽的天气让庙会进入游园高峰，单日接待量较前日增长了约50%．大年初五，活动进入尾声，但庙会现场仍然人头攒动，仍约有5.5万人次来园参观．‎ ‎（1）直接写出扇形统计图中m的值；‎ ‎（2）初四这天，庙会接待游客量约_______万人次；‎ ‎（3）请用统计图或统计表，将庙会期间每日接待游客的人数表示出来．‎ ‎25．如图，⊙O为等腰三角形ABC的外接圆，AB=AC，AD是⊙O的直径，切线DE与AC的延长线相交于点E．‎ ‎（1）求证：DE∥BC；‎ ‎（2）若DF=n，∠BAC=2α，写出求CE长的思路． ‎ ‎26．有这样一个问题：探究函数的图象与性质． 小军根据学习函数的经验， 对函数的图象与性质进行了探究． 下面是小军的探究过程， 请补充完整：‎ ‎（1）函数的自变量x的取值范围是 ；‎ ‎（2）下表是y与x的几组对应值 x ‎﹣2‎ ‎﹣1.9‎ ‎﹣1.5‎ ‎﹣1‎ ‎﹣0.5‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ y ‎2‎ ‎1.60‎ ‎0.80‎ ‎0‎ ‎﹣0.72‎ ‎﹣1.41‎ ‎﹣0.37‎ ‎0‎ ‎0.76‎ ‎1.55‎ ‎…‎ 在平面直角坐标系xOy中， 描出了以上表中各对对应值为坐标的点，根据描出的点， 画出该函数的图象；‎ ‎（3）观察图象，函数的最小值是 ；‎ ‎（4）进一步探究，结合函数的图象， 写出该函数的一条性质（函数最小值除外）： ．‎ ‎27．直线与x轴，y轴分别交于A，B两点，点A关于直线的对称点为点C．‎ ‎（1）求点C的坐标；‎ ‎（2）若抛物线经过A，B，C三点，求该抛物线的表达式；‎ ‎（3）若抛物线 经过A，B两点，且顶点在第二象限，抛物线与线段AC有两个公共点，求a的取值范围．‎ ‎ ‎ ‎28．在△ABC中，AB=AC，∠A=60°，点D是BC边的中点，作射线DE，与边AB交于点E，射线DE绕点D顺时针旋转120°，与直线AC交于点F．‎ ‎（1）依题意将图1补全；‎ ‎（2）小华通过观察、实验提出猜想：在点E运动的过程中，始终有DE=DF．小华把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：‎ 想法1：由点D是BC边的中点，通过构造一边的平行线，利用全等三角形，可证DE=DF； ‎ 想法2：利用等边三角形的对称性，作点E关于线段AD的对称点P，由∠BAC与∠EDF互补，可得∠AED与∠AFD互补，由等角对等边，可证DE=DF；‎ 想法3：由等腰三角形三线合一，可得AD是∠BAC的角平分线，由角平分线定理，构造点D到AB，AC的高，利用全等三角形，可证DE=DF…….‎ 请你参考上面的想法，帮助小华证明DE=DF（选一种方法即可）；‎ ‎（3）在点E运动的过程中，直接写出BE，CF，AB之间的数量关系．‎ 图1‎ 备用图 ‎29．在平面直角坐标系中，点Q为坐标系上任意一点，某图形上的所有点在∠Q的内部（含角的边），这时我们把∠Q的最小角叫做该图形的视角．如图1，矩形ABCD，作射线OA，OB，则称∠AOB为矩形ABCD的视角．‎ 图2‎ 备用图 图1‎ （1） 如图1，矩形ABCD，A（﹣，1），B（，1），C（，3），D（﹣，3），直接写出视角∠AOB的度数；‎ ‎（2）在（1）的条件下，在射线CB上有一点Q，使得矩形ABCD的视角∠AQB=60°，求点Q的坐标；‎ ‎（3）如图2，⊙P的半径为1，点P（1，），点Q在x轴上，且⊙P的视角∠EQF的度数大于60°，若Q（a，0），求a的取值范围．‎ 平谷区2016—2017学年度初三统练（一）‎ 数学答案 2017.4‎ 一、选择题(本题共30分，每小题3分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B B A C D D C B A C 二、填空题（本题共18分，每小题3分）‎ ‎11．3；12．； 13．答案不唯一，如；14．0.50； 15．2.7；‎ ‎16．两直线平行，内错角相等； 1‎ 等腰三角形两底角相等； 3‎ ‎（其他正确依据也可以）．‎ 三、解答题（本题共72分，第17-26题，每小题5分，第27题7分，第28题7分，第29题8分）解答应写出文字说明、演算步骤或证明过程.‎ ‎17．解：‎ ‎= 4‎ ‎=﹣2． 5‎ ‎18．解：，‎ 解不等式①得x≤1， 1‎ 解不等式②得x＞﹣3， 2‎ ‎∴不等式组的解集是：﹣3＜x≤1． 3‎ ‎∴不等式组的非负整数解为0，1． 5‎ ‎19．证明：∵矩形ABCD，‎ ‎∴AD∥BC．‎ ‎∴∠ADE=∠DEC． 1‎ ‎∵AF⊥DE于F，‎ ‎∴∠AFD=∠C=90°． 2‎ ‎∵DE=DA， 3‎ ‎∴△ADF≌△DEC． 4‎ ‎∴AF=CD． 5‎ ‎20．（1）证明: ∵ Δ=[-(m+2)]2-4×2m 1‎ ‎=(m-2)2  ‎∵ (m-2)2≥0，‎ ‎∴方程总有两个实数根． 2‎ ‎（2）当m=2时，原方程变为x2-4x+4=0． 3‎ 解得x1=x2=2． 5‎ ‎21．解：（1）∵双曲线经过点，A（﹣2，3），∴． 1‎ ‎∵直线经过点A（﹣2，3），∴． 2‎ ‎∴此直线与x轴交点B的坐标为（1，0）. 3‎ ‎（2）(0，3)，(0，-1)． 5‎ ‎22．解：设去年该型号自行车每辆售价x元，则今年每辆售价为（x﹣200）元． 1‎ 由题意，得， 2‎ 解得：x=2000． 3‎ 经检验，x=2000是原方程的根． 4‎ 答：去年该型号自行车每辆售价为2000元． 5‎ ‎23．（1）证明：∵EF垂直平分BD，‎ ‎∴EB=ED，FB=FD． 1‎ ‎∵BD平分∠ABC交AC于D，‎ ‎∴∠ABD=∠CBD．‎ ‎∵∠ABD+∠BEG=90°，∠CBD+∠BFG=90°，‎ ‎∴∠BEG=∠BFG．‎ ‎∴BE=BF．‎ ‎∴四边形BFDE是菱形．‎ ‎∴DE=DF． 2‎ ‎（2）解：过D作DH⊥CF于H．‎ ‎∵四边形BFDE是菱形，∴DF∥AB，DE=DF=4．‎ 在Rt△DFH中，∠DFC=∠ABC=30°，∴DH=2．‎ ‎∴FH=． 3‎ 在Rt△CDH中，∠C=45°，‎ ‎∴DH=HC=2． 4‎ ‎∴CF=2+． 5‎ ‎24．（1）扇形统计图中m的值是25.1%； 1‎ ‎（2）6； 2‎ ‎（3）如图． 5‎ ‎25．（1）证明：∵AB=AC，AD是⊙O的直径，∴AD⊥BC于F． 1‎ ‎∵DE是⊙O的切线，∴DE⊥AD于D．∴DE∥BC． 2‎ ‎（2）连结CD．‎ 由AB=AC，∠BAC=2α，可知∠BAD=α． 3‎ 由同弧所对的圆周角，可知∠BCD=∠BAD=α．‎ 由AD⊥BC，∠BCD =α，DF=n，‎ 根据sinα=，可知CD的长． 4‎ 由勾股定理，可知CF的长 由DE∥BC，可知∠CDE=∠BCD．‎ 由AD是⊙O的直径，可知∠ACD=90°．‎ 由∠CDE=∠BCD，∠ECD=∠CFD，‎ 可知△CDF∽△DEC，可知，可求CE的长． 5‎ ‎26．（1）； 1‎ ‎（2）该函数的图象如图所示； 3‎ ‎（3）； 4‎ ‎（4）该函数的其它性质:当时，y随x的增大而减小； 5‎ ‎（答案不唯一，符合函数性质即可写出一条即可）‎ ‎27．解：（1）令y=0，得x=1．‎ ‎∴点A的坐标为（1,0）． 1‎ ‎∵点A关于直线x=﹣1对称点为点C，‎ ‎∴点C的坐标为（﹣3,0）． 2‎ ‎（2）令x=0，得y=3．‎ ‎∴点B的坐标为（0,3）．‎ ‎∵抛物线经过点B，‎ ‎∴﹣3m=3，解得m=﹣1． 3‎ ‎∵抛物线经过点A，‎ ‎∴m+n﹣3m=0，解得n=﹣2．‎ ‎∴抛物线表达式为． 4‎ ‎（3）由题意可知，a<0．‎ 根据抛物线的对称性，当抛物线经过（﹣1,0）时，开口最小，a=﹣3， 5‎ 此时抛物线顶点在y轴上，不符合题意.‎ 当抛物线经过（﹣3,0）时，开口最大，a=﹣1. 6‎ 结合函数图像可知，a的取值范围为. 7‎ ‎28．解：（1）如图1， 1‎ 图1‎ ‎（2）‎ 图2‎ 图3‎ 图4‎ 想法1证明：如图2，过D作DG∥AB，交AC于G， 2‎ ‎∵点D是BC边的中点，‎ ‎∴DG=AB．‎ ‎∴△CDG是等边三角形．‎ ‎∴∠EDB+∠EDG=120°．‎ ‎∵∠FDG+∠EDG=120°，‎ ‎∴∠EDB =∠FDG． 3‎ ‎∵BD=DG，∠B=∠FGD=60°，‎ ‎∴△BDE≌△GDF． 4‎ ‎∴DE=DF． 5‎ 想法2证明：如图3，连接AD，‎ ‎∵点D是BC边的中点，‎ ‎∴AD是△ABC的对称轴．‎ 作点E关于线段AD的对称点P，点P在边AC上， 2‎ ‎∴△ADE≌△ADP．‎ ‎∴DE=DP，∠AED=∠APD．‎ ‎∵∠BAC+∠EDF=180°，‎ ‎∴∠AED+∠AFD=180°．‎ ‎∵∠APD+∠DPF=180°，‎ ‎∴∠AFD=∠DPF． 3‎ ‎∴DP=DF． 4‎ ‎∴DE=DF． 5‎ 想法3证明：如图4，连接AD，过D作DM⊥AB于M，DN⊥AB于N， 2‎ ‎∵点D是BC边的中点，‎ ‎∴AD平分∠BAC．‎ ‎∵DM⊥AB于M，DN⊥AB于N，‎ ‎∴DM=DN． 3‎ ‎∵∠A=60°，‎ ‎∴∠MDE+∠EDN=120°．‎ ‎∵∠FDN+∠EDN=120°，‎ ‎∴∠MDE=∠FDN．‎ ‎∴Rt△MDE≌Rt△NDF． 4‎ ‎∴DE=DF． 5‎ ‎（3）当点F在AC边上时，； 6‎ 当点F在AC延长线上时，． 7‎ ‎29．解：（1）120°； 1‎ ‎（2）连结AC，在射线CB上截取CQ=CA，连结AQ． 2‎ ‎∵AB=2，BC=2，‎ ‎∴AC=4． 3‎ ‎∴∠ACQ=60°．‎ ‎∴△ACQ为等边三角形，‎ 即∠AQC=60°． 4‎ ‎∵CQ=AC=4，‎ ‎∴Q（，﹣1）． 5‎ ‎（3）‎ 图2‎ 图1‎ 如图1，当点Q与点O重合时，∠EQF=60°，‎ ‎∴Q（0，0）． 6‎ 如图2，当FQ⊥x轴时，∠EQF=60°，‎ ‎∴Q（2，0）． 7‎ ‎∴a的取值范围是0＜a＜2． 8‎