2014贵州省安顺市中考数学试卷2 12页

‎2014年贵州省安顺市中考试卷 数 学 ‎（满分150分，考试时间120分钟）‎ 一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的。）‎ ‎1.（2014贵州省安顺市，1，3分）若一个数的相反数是3，则这个数是（ ）‎ A． B． C．﹣3 D．3‎ ‎【答案】C ‎2. （2014贵州省安顺市，2，3分）地球上的陆地面积约为149000000km2,将149000000用科学计数法表示为（ ）‎ A．1.49×106 B．1.49×107 C．1.49×108 D．1.49×109‎ ‎【答案】C ‎3. （2014贵州省安顺市，3，3分）下列四个图形中，既是轴对称图形又是中心对称图形的有（ ）‎ A．1个 B．2个 C．3个 D．4个 ‎【答案】B ‎4. （2014贵州省安顺市，4，3分）用直尺和圆规作一个角等于已知角，如图，能得出∠A’O’B’=∠AOB的依据是（ ）‎ A．（SAS） B．（SSS） C．（ASA） D．（AAS）‎ ‎【答案】B ‎5. （2014贵州省安顺市，5，3分）如图，∠AOB的两边OA、OB均为平面反光镜，∠AOB=40°，在射线OB上有一点P，从点P点射出的一束光线经OA上的Q 点反射后，反射光线QR恰好与OB平行，则∠QPB的度数是（ ）‎ A．60° B．80° C．100° D．120°‎ ‎【答案】B ‎6. （2014贵州省安顺市，6，3分）已知等腰三角形的两边长分别为a、b，且a、b满足，则此等腰三角形的周长为（ ）‎ A．7或8 B．6或10 C．6或7 D．7或10‎ ‎【答案】A ‎7. （2014贵州省安顺市，7，3分）如果点A（-2，y1）,B(-1,y2),C(2,y3)都在反比例函数（k>0）的图象上，那么，y1，y2，y3的大小关系是（ ）‎ A． B． ‎ C． D．‎ ‎【答案】B ‎8. jscm（2014贵州省安顺市，8，3分）已知圆锥的母线长为6cm，底面圆的半径为3cm，则此圆锥侧面展开图的圆心角的度数是（ ）‎ A．30° B．60° C．90° D．180°‎ ‎【答案】D ‎9. 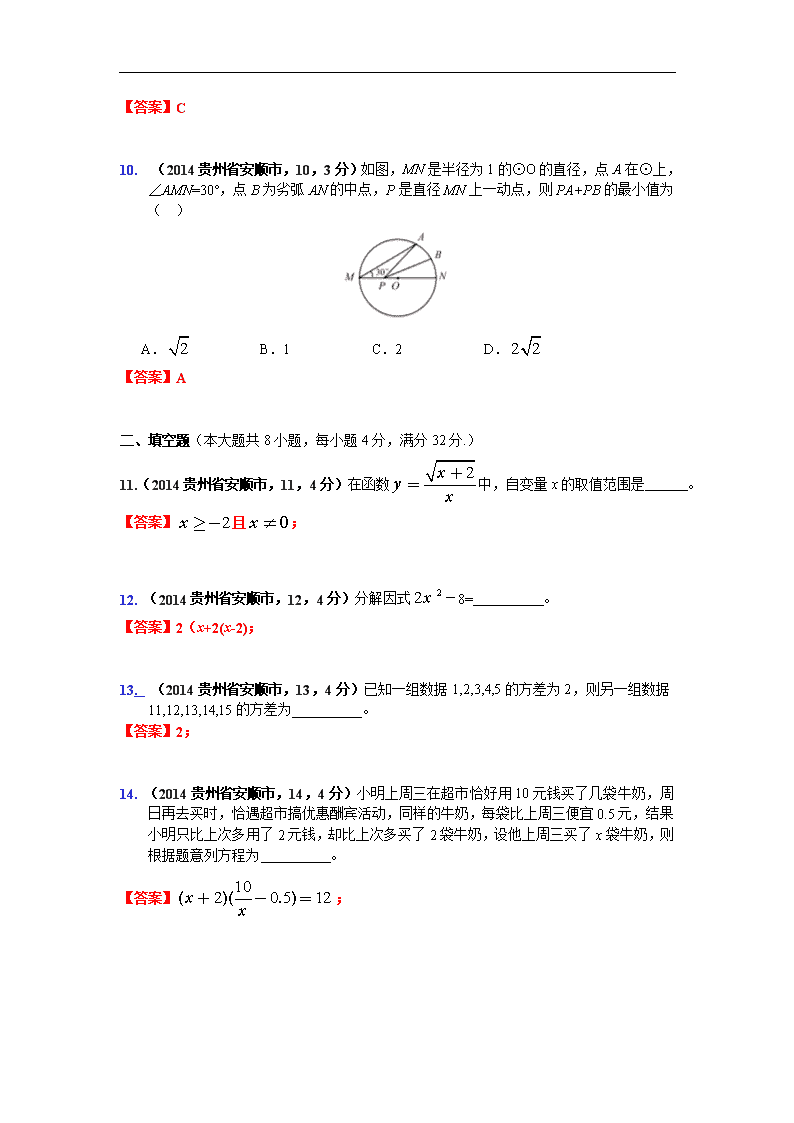jscm（2014贵州省安顺市，9，3分）如图，在Rt△ABC中，∠C=90°，∠A=30°，E为线段AB上一点且AE:EB=4：1，EF⊥AC于F，连接FB，则tan∠CFB的值等于（ ）‎ A． B． C． D．‎ ‎【答案】C ‎10. jscm（2014贵州省安顺市，10，3分）如图，MN是半径为1的⊙O的直径，点A在⊙上，∠AMN=30°，点B为劣弧AN的中点，P是直径MN上一动点，则PA+PB的最小值为（ ）‎ A． B．1 C．2 D．‎ ‎【答案】A 二、填空题（本大题共8小题，每小题4分，满分32分.）‎ ‎11.（2014贵州省安顺市，11，4分）在函数中，自变量x的取值范围是 。‎ ‎【答案】且；‎ ‎12. （2014贵州省安顺市，12，4分）分解因式－8= 。‎ ‎【答案】2（x+2(x-2)；‎ ‎13. （2014贵州省安顺市，13，4分）已知一组数据1,2,3,4,5的方差为2，则另一组数据11,12,13,14,15的方差为 。‎ ‎【答案】2；‎ ‎14. （2014贵州省安顺市，14，4分）小明上周三在超市恰好用10元钱买了几袋牛奶，周日再去买时，恰遇超市搞优惠酬宾活动，同样的牛奶，每袋比上周三便宜0.5元，结果小明只比上次多用了2元钱，却比上次多买了2袋牛奶，设他上周三买了x袋牛奶，则根据题意列方程为 。‎ ‎【答案】；‎ ‎15. （2014贵州省安顺市，15，4分）不等式组的整数解为 。‎ ‎【答案】-1,0,1；‎ ‎16. （2014贵州省安顺市，16，4分）如图，矩形ABCD沿着对角线BD折叠，使点C落在C’处，BC’交AD于点E，AD=8，AB=4，则DE的长为 。‎ ‎【答案】5；‎ ‎17. jscm（2014贵州省安顺市，17，4分）如图，∠AOB=45°，过射线OA上到点O的距离分别为1,3,5,7,9,11，……的点作OA的垂线与OB相交，得到并标出一组黑色梯形，它们的面积分别为……。观察图中的规律，则第n(n为正整数)个黑色梯形的面积= 。‎ ‎【答案】8n-4；‎ ‎18.jscm（2014贵州省安顺市，18，4分）如图，二次函数（a>0）的图象的顶点为点D，其图象与x轴的交点A、B的横坐标分别为﹣1,3，与y轴负半轴交于点C。在下面五个结论中：①2a-b=0；②a+b+c>0；③c=-3a；④只有当a=时，△ABD是等腰直角三角形；⑤使△ACB为等腰三角形的a的值可以有四个。其中正确的结论是 。（只填序号）‎ ‎【答案】③，④；‎ 三、解答题（本大题共8小题，满分88分，解答应写出文字说明、证明过程或演算步骤）‎ ‎19. （2014贵州省安顺市，19，8分）计算：‎ ‎【答案】解：原式=1+3+4×－……………………………………4分 ‎ =4+-……………………………………………………6分 ‎ =4……………………………………………………………………8分 ‎20. （2014贵州省安顺市，20，10分）先化简，再求值：，其中x=2。‎ ‎【答案】解：原式=……………………………………2分 ‎ =……………………………………4分 ‎=……………………………………6分 ‎=……………………………………8分 当x=2时，原式=……………………………………10分 ‎21.（2014贵州省安顺市，21，10分）‎ 天山旅行社为吸引顾客组团去具有科斯塔地貌特征的黄果树风景区旅游，推出了如下收费标准（如图所示）：‎ ‎ 某单位组织员工去具有科斯塔地貌特征的黄果树风景区旅游，共支付给天山旅行社旅游费用27000元，请问该单位这次共有多少名员工去具有科斯塔地貌特征的黄果树风景区旅游？‎ ‎【答案】解：设该单位这次共有x名员工去具有科斯塔地貌特征的黄果树风景区旅游……………………………………1分 ‎ 因为1000×25=25000<27000，所以员工人数一定超过25人……………………2分 ‎ 可列方程【1000-20×（x-25）】x=27000……………………………………5分 ‎ 整理，得：，解得：，………8分 ‎ 当时，1000-20×（x-25）=600<700，故舍去；‎ ‎ 当时，1000-20×（x-25）=900>700,符合题意。…………………9分 ‎ 答：该单位这次共有30名员工去具有科斯塔地貌特征的黄果树风景区旅游。‎ ‎ ……………………………………10分 ‎22. jscm（2014贵州省安顺市，22，10分）如图，点A(m，m+1)，B(m+3,m-1)是反比例函数（k>0）与一次函数y=ax+b的交点。‎ ‎（1）求反比例函数与一次函数的解析式；‎ ‎（2）根据图象直接写出当反比例函数的函数值大于一次函数的函数值时x的取值范围。‎ ‎【答案】解：（1）由题意可知，m(m+1)=(m+3)(m-1)，解得m=3. ……………………2分 ‎ ∴A(3，4)，B（6,2）；‎ ‎ ∴k=4×3=12.∴……………………………………………………4分 ‎ ∵点A的坐标为(3，4)，点B的坐标为（6,2）‎ ‎ ∴ ∴ ∴……………………6分 ‎ （2）解：根据题意可得：=，‎ 化简得：，解得：‎ ‎∴根据图象得x的取值范围：06。………………………10分 ‎23. （2014贵州省安顺市，23，12分）如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC的外角∠CAM的平分线，CE⊥AN，垂足为点E。‎ （1） 求证：四边形ADCE为矩形；‎ （2） 当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明。‎ ‎【答案】解：证明：（1）在△ABC中，AB=AC，AD⊥BC，∴∠BAD=∠DAC。∵AN是△ABC的外角∠CAM的平分线，∴∠MAE=∠CAE。∴∠DAE=∠DAC+∠CAE=×180°=90°。‎ ‎ 又∵AD⊥BC，CE⊥AN，∴∠ADC=∠CEA=90°。‎ ‎ ∴四边形ADCE为矩形。……………………………………………………6分 （2） 例如，当∠BAC=90°时，四边形ADCE是正方形。‎ 证明：∵∠BAC=90°，AB=AC，AD⊥BC于D，‎ ‎ ∴∠ACD=∠DAC=45°，∴DC=AD。‎ ‎ 由（1）四边形ADCE为矩形，∴矩形ADCE是正方形。……………12分 ‎24. （2014贵州省安顺市，24，12分）学校举办一项小制作评比活动，作品上交时限为‎3月1日至30日，组委会把同学们交来的作品按时间顺序每5天组成一组，对每一组的作品件数进行统计，绘制成如图所示的统计图。已知从左到右各矩形的高度比为2:3:4:6:4:1，第三组的件数是12。‎ ‎ 请你回答：‎ ‎ （1）本次活动共有 件作品参赛；各组作品件数的众数是 件。‎ ‎ （2）经评比，第四组和第六组分别有10件和2件作品获奖，那么你认为这两组哪个组获奖率高？为什么？‎ ‎ （3）小制作评比结束后，组委会决定从4件最优秀的作品A、B、C、D中选出两件进行全校展示，请用树状图或列表法求出刚好展示作品B、D的概率。‎ ‎【答案】解：（1）本次活动共有：（件），则各组作品的件数分别为：6,9,12,18,12,3，∴众数为12。………………………………………2分 ‎ （2）解：第四组有作品：（件）‎ ‎ 第六组有作品（件）‎ ‎ ∴第四组的获奖率为，第六组的获奖率为。‎ ‎ ∵，∴第六组的获奖率高。……………………………………6分 （2） 画树状图或列表如下 由表（图）知，所有等可能的结果共有12种，其中刚好是（B，D）的有2种，所有刚好展示作品（B，D）的概率为P=。………………………………………………12分 ‎25. （2014贵州省安顺市，25，12分）如图，已知AB是⊙O的直径，BC是⊙O的弦，弦ED⊥AB于点F，交BC于点G，过点C的直线与ED的延长线交于点P，PC=PG。‎ ‎ （1）求证：PC是⊙O的切线；‎ ‎ （2）当点C在劣弧AD上运动时，其他条件不变，若，求证：点G是BC的中点；‎ ‎ （3）在满足（2）的条件下，若AB=10，ED=，求BG的长。‎ ‎【答案】解：（！）连接OC，∵ED⊥AB，∴∠BFG=90°。‎ ‎ ∴∠B+∠BGF=90°。‎ ‎ 又∵PC=PG，∴∠PCG=∠PGC。‎ ‎ 而∠PGC=∠BGF。∴∠B+∠PCG=90°。‎ 又∵OB=OC，∴∠B=∠BCO。‎ ‎∴∠BCO+∠PCG=90°，则∠PCO=90°，即OC⊥PC。‎ 而OC是半径，∴PC是⊙O的切线。…………………………………4分 ‎（2）连接OG，∵，∴，而∠B=∠B ‎ ∴△BFG∽△BGO，∴∠BGO=∠BFG=90°，‎ ‎ ∴OG⊥BC，∴点G是BC的中点。………………………………………………8分 ‎（3）连接OE，∵AB是⊙O的直径，ED⊥AB，∴EF=ED。‎ ‎∵AB=10，ED=，∴EF=，OE=OB=AB=5。‎ 在Rt△OEF中，OF==1，∴BF=OB-OF=5-1=4.‎ ‎∴BG==。………………………………………………12分 ‎26. （2014贵州省安顺市，26，14分）如图，在平面直角坐标系中，四边形ABCD是等腰梯形，AD∥BC，AB=DC，BC在x轴上，点A在y轴的正半轴上，点A、D的坐标分别为A(0，2)，D(2，2)，AB=，连接AC。‎ （1） 求出直线AC的函数解析式；‎ （2） 求过点A、C、D的抛物线的函数解析式；‎ （3） 在抛物线上有一点P（m，n）（n<0），过点P作PM垂直于x轴，垂足为M，连接PC，使以点C、P、M为顶点的三角形与Rt△AOC相似，求出点P的坐标。‎ ‎【答案】解：（1）由A（0,2）知OA=2，在Rt△ABO中，∵AB=，‎ ‎ ∴OB===2‎ ‎ 则B(-2，0)，根据等腰梯形的轴对称性可得C点坐标为（4,0）………………1分 ‎ 设直线的函数解析式为y=kx+b ‎ ∴ ∴ ∴…………………………3分 （2） 过A、C、D三点得抛物线的解析式为y=‎ ‎∴ ∴ ∴………………6分 ‎（3）∵P（m，n）（n<0）在抛物线上，‎ ‎ ∴m>4,或m<-2，n=<0。∴PM=‎ ‎ ∵Rt△PCM与Rt△AOC相似，∴或 ‎ 若m<-2，则MC=4-m，当时，，‎ ‎ 解得：（舍），此时P(-4，-4) ……………………………8分 ‎ 当时，‎ 解得：（舍），此时P(-10，-28) …………………………………10分 若m>4，则MC=m-4，‎ 当时，，‎ ‎ 解得：（舍），（舍）………………………………………12分 ‎ 当时，‎ 解得：（舍），此时P(6，-4)‎ 综上所述，点P的坐标为(-4，-4)，(6，-4)，(-10，-28)。………………………………14分