中考数学综合题专题成都中考B卷培优专题训练一 5页

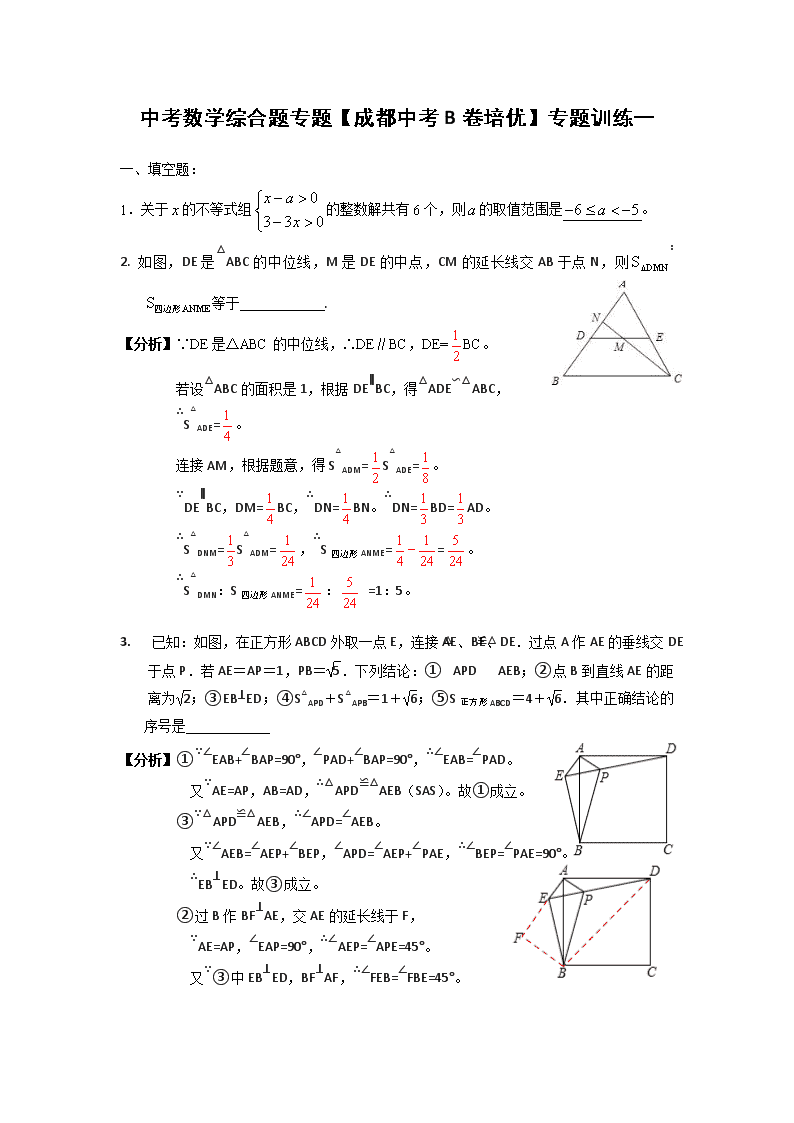
中考数学综合题专题【成都中考B卷培优】专题训练一 一、填空题：‎ ‎1．关于的不等式组的整数解共有6个，则的取值范围是。‎ ‎2. 如图，DE是△ABC的中位线，M是DE的中点，CM的延长线交AB于点N，则∶等于 .‎ ‎【分析】∵DE是△ABC的中位线，∴DE∥BC，DE=BC。‎ 若设△ABC的面积是1，根据DE∥BC，得△ADE∽△ABC，‎ ‎∴S△ADE=。‎ 连接AM，根据题意，得S△ADM=S△ADE=。‎ ‎∵DE∥BC，DM=BC，∴DN=BN。∴DN=BD=AD。‎ ‎∴S△DNM=S△ADM=，∴S四边形ANME==。‎ ‎∴S△DMN：S四边形ANME=： =1：5。‎ ‎3. 已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE＝AP＝1，PB＝．下列结论：①△APD≌△AEB；②点B到直线AE的距 ‎ 离为；③EB⊥ED；④S△APD＋S△APB＝1＋；⑤S正方形ABCD＝4＋．其中正确结论的序号是 ‎ ‎【分析】①∵∠EAB+∠BAP=90°，∠PAD+∠BAP=90°，∴∠EAB=∠PAD。‎ 又∵AE=AP，AB=AD，∴△APD≌△AEB（SAS）。故①成立。‎ ‎③∵△APD≌△AEB，∴∠APD=∠AEB。‎ 又∵∠AEB=∠AEP+∠BEP，∠APD=∠AEP+∠PAE，∴∠BEP=∠PAE=90°。‎ ‎∴EB⊥ED。故③成立。‎ ‎②过B作BF⊥AE，交AE的延长线于F，‎ ‎∵AE=AP，∠EAP=90°，∴∠AEP=∠APE=45°。‎ 又∵③中EB⊥ED，BF⊥AF，∴∠FEB=∠FBE=45°。‎ 又∵，∴BF=EF=。‎ 故②不正确。‎ ‎④如图，连接BD，在Rt△AEP中，∵AE=AP=1，∴EP=。‎ 又∵PB=，∴BE=。∵△APD≌△AEB，∴PD=BE=。‎ ‎∴S△ABP＋S△ADP=S△ABD－S△BDP=S正方形ABCD－×DP×BE=。‎ 故④不正确。‎ ‎⑤∵EF=BF=，AE=1，∴在Rt△ABF中，，‎ ‎∴S正方形ABCD= 。故⑤正确。综上所述，正确结论的序号是①③⑤。‎ 二、 解答题 4、 如图，在直角三角形ABC中，，AD是的角平分线，DE//CA，已知CD=12，BD=15，求AE、BE的长。‎ ‎    分析：题目要求AE、BE这两个未知数的值，由于DE//CA，并且DC=12，BD=15，容易得到，得到关于BE、EA的一个方程。而题目中有两个未知数，还需要再建立一个关于BE、EA的方程。‎ ‎    由条件易知，ABC和EBD都是直角三角形，由AD是角平分线和DE//CA可以证明AE=ED，这样就把AE、EB集中在RtEDB中，用勾股定理可再列一个方程。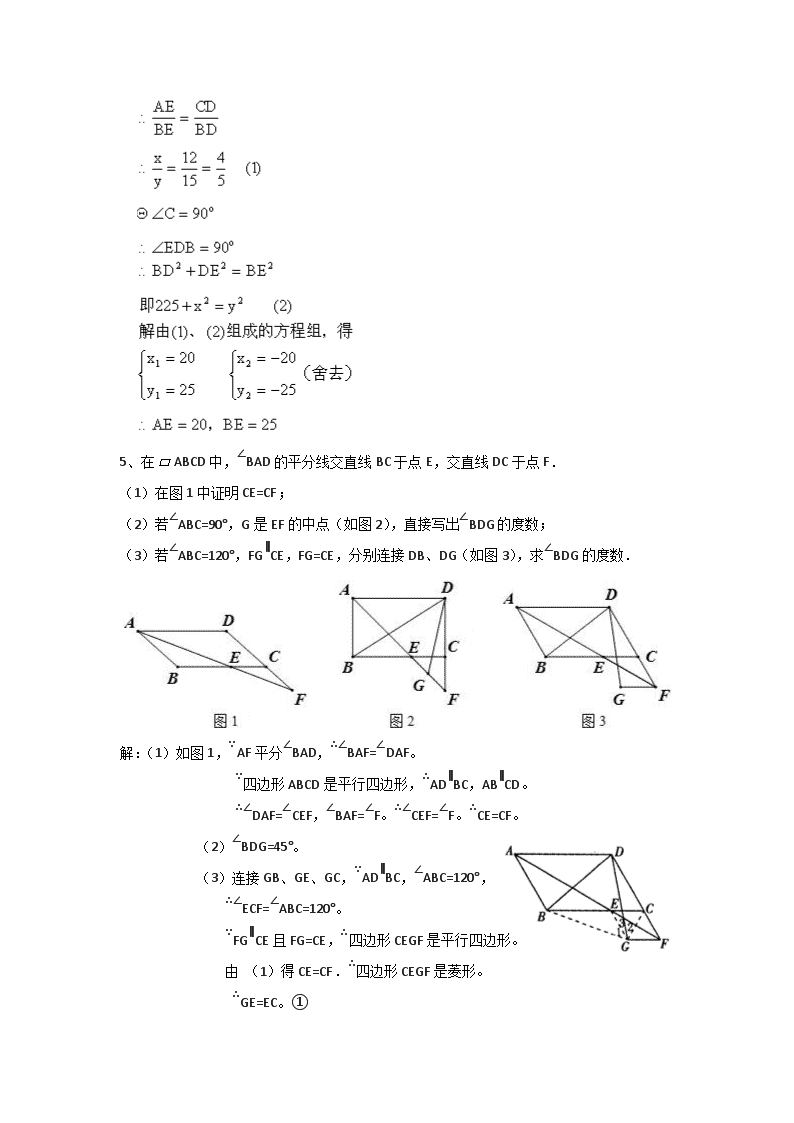‎ ‎    解：‎ ‎    ‎ ‎    设AE为x，BE为y，那么 ‎    ‎ ‎    ‎ ‎    ‎ ‎    ‎ ‎    ‎ ‎    ‎ ‎5、在ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．‎ ‎（1）在图1中证明CE=CF；‎ ‎（2）若∠ABC=90°，G是EF的中点（如图2），直接写出∠BDG的度数；‎ ‎（3）若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图3），求∠BDG的度数．‎ 解：（1）如图1，∵AF平分∠BAD，∴∠BAF=∠DAF。‎ ‎ 　　 ∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD。‎ ‎ 　　 ∴∠DAF=∠CEF，∠BAF=∠F。∴∠CEF=∠F。∴CE=CF。‎ ‎ （2）∠BDG=45°。‎ ‎ （3）连接GB、GE、GC，∵AD∥BC，∠ABC=120°，‎ ‎ 　 ∴∠ECF=∠ABC=120°。‎ ‎ 　 ∵FG∥CE且FG=CE，∴四边形CEGF是平行四边形。‎ ‎ 　 由 （1）得CE=CF．∴四边形CEGF是菱形。‎ ‎∴GE=EC。①‎ ‎ 　∵ ∠GCF=∠GCE=∠ECF=60°，∴△ECG是等边三角形。‎ ‎ 　 ∴EG=CG，∠GEC=∠EGC。∴∠GEC=∠FGC。∴∠BEG=∠DCG。②‎ ‎ 　由AD∥BC及AF平分∠BAD可得∠BAE=∠AEB，∴AB=BE。‎ ‎ 　在ABCD中，AB=DC，∴BE=DC，③‎ ‎ 　 由①②③得△BEG≌△DCG（SAS）。∴BG=DG，∠1=∠2。‎ ‎ 　∴∠BGD=∠1+∠3=∠2+∠3=∠EGC=60°，‎ ‎ 　 ∴∠BDG==60°。‎ ‎6．某通信器材公司销售一种市场需求较大的新型通讯产品。已知每件产品的进价为40元，每年销售该种产品的总开支（不含进价）总计120万元。在销售过程中发现，年销售量y（万件）与销售单价（元）之间存在着一次函数关系，其中整数 k使式子有意义。经测算，销售单价60元时，年销售量为50000件。‎ ‎ （1）求出这个函数关系式；‎ ‎ （2）试写出该公司销售该种产品的年获利z（万元）关于销售单价（元）的函数关系式（年获利=年销售额—年销售产品总进价—年总开支）。当销售单价为何值时，年获利最大？并求这个最大值；‎ （3） 若公司希望该种产品一年的销售获利不低于40万元，借助（2）中函数的图像，请你帮助该公司确定销售单价的范围。在此情况下，要使产品销售量最大，你认为销售单价应定为多少元？‎ ‎ 解：（1）由 ‎…………………………………………………………………………1分 当k=1时，年销售量随售价增大而增大，不合。‎ ‎…………………………………………………………………2分 ‎ 把 ‎…………………………………………………………………………3分 ‎ ‎（2）‎ ‎……………4分 ‎ 当元时，年获利最大值为60万元。……5分 ‎ ‎（3）令 整理得 ……………………………………………………………6分 解得：。…………………………………………………………………7分 ‎ 由图象可知，（画图并标上数据1分）要使年获利不低于40万元，销售单价应在80元到120元之间，（说明此点1分）又因为销售单价越低，销售量越大，所以要使销售量最大，又要使年获利不低于40万元，则销售单价应定为80元。（说明此点1分）…………10分