济南市中考数学27题9分训练 13页

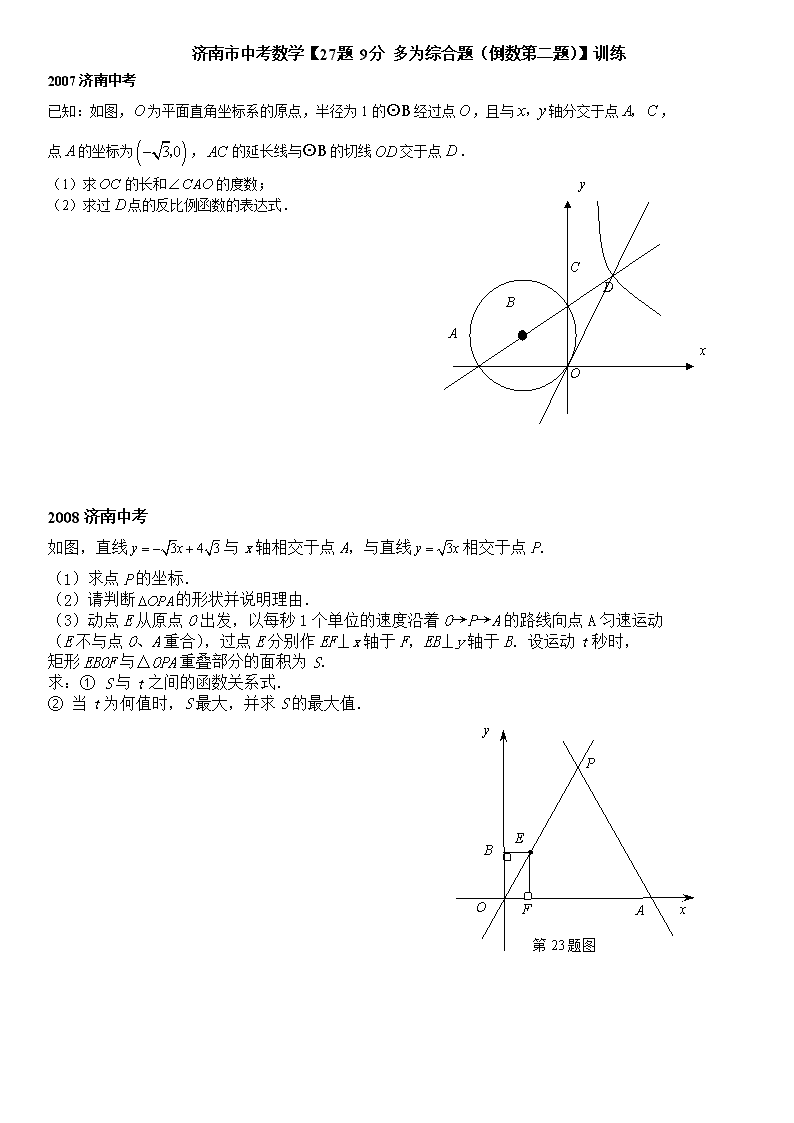
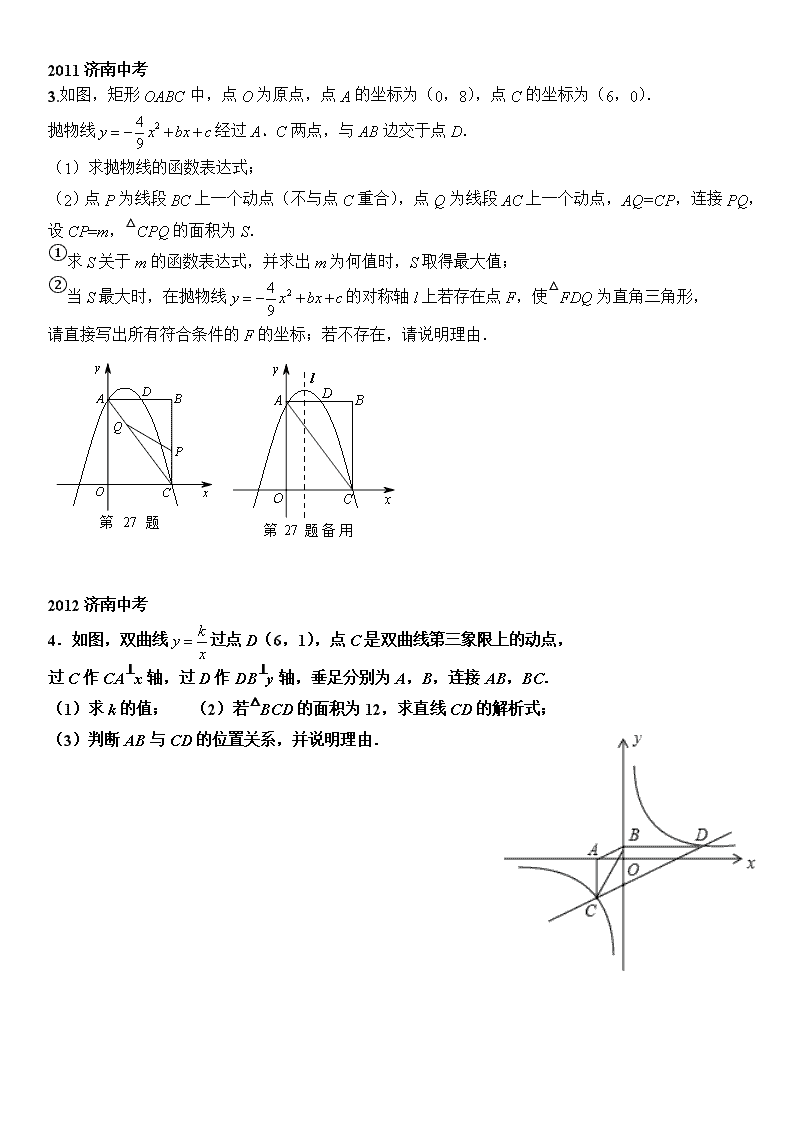
济南市中考数学【27题 9分 多为综合题（倒数第二题）】训练 ‎2007济南中考 已知：如图，为平面直角坐标系的原点，半径为1的⊙B经过点，且与轴分交于点，‎ B A C D y x O 点的坐标为，的延长线与⊙B的切线交于点．‎ ‎（1）求的长和的度数；‎ ‎（2）求过点的反比例函数的表达式．‎ ‎ ‎ ‎2008济南中考 如图，直线与x轴相交于点A，与直线相交于点P．‎ ‎（1）求点P的坐标．‎ ‎（2）请判断的形状并说明理由．‎ ‎（3）动点E从原点O出发，以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动 ‎（E不与点O、A重合），过点E分别作EF⊥x轴于F，EB⊥y轴于B．设运动t秒时，‎ 矩形EBOF与△OPA重叠部分的面积为S．‎ 求：① S与t之间的函数关系式．‎ ‎② 当t为何值时，S最大，并求S的最大值．‎ F 第23题图 y O A x P E B ‎2009济南中考 ‎1、如图，在梯形中，‎ 动点从点出发沿线段以每秒2个单位长度的速度向终点运动；‎ 动点同时从点出发沿线段以每秒1个单位长度的速度向终点运动．设运动的时间为秒．‎ ‎（1）求的长．‎ ‎（2）当时，求的值．‎ A D C B M N ‎（第1题图）‎ ‎（3）试探究：为何值时，为等腰三角形．‎ ‎2010济南中考 ‎2.已知：△ABC是任意三角形．‎ ‎⑴如图1所示，点M、P、N分别是边AB、BC、CA的中点．求证：∠MPN=∠A．‎ ‎⑵如图2所示，点M、N分别在边AB、AC上，且，，点P1、P2是边BC的三等分点，‎ 你认为∠MP1N+∠MP2N=∠A是否正确？请说明你的理由．‎ ‎⑶如图3所示，点M、N分别在边AB、AC上，且，，点P1、P2、……、‎ P2009是边BC的2010等分点，则∠MP1N+∠MP2N+……+∠MP2009N=____________．‎ ‎（请直接将该小问的答案写在横线上．）‎ A B C N M P A M N P1‎ C P2‎ B A C M N P1‎ P2‎ P2009‎ ‎……‎ ‎……‎ B 第23题图2‎ 第23题图1‎ 第23题图3‎ ‎2011济南中考 ‎3.如图，矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．‎ 抛物线经过A、C两点，与AB边交于点D．‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，‎ 设CP=m，△CPQ的面积为S．‎ ‎①求S关于m的函数表达式，并求出m为何值时，S取得最大值；‎ ‎②当S最大时，在抛物线的对称轴l上若存在点F，使△FDQ为直角三角形，‎ 请直接写出所有符合条件的F的坐标；若不存在，请说明理由．‎ 第27题图 l 第27题备用图 ‎2012济南中考 ‎4．如图，双曲线过点D（6，1），点C是双曲线第三象限上的动点，‎ 过C作CA⊥x轴，过D作DB⊥y轴，垂足分别为A，B，连接AB，BC．‎ ‎（1）求k的值； （2）若△BCD的面积为12，求直线CD的解析式；‎ ‎（3）判断AB与CD的位置关系，并说明理由．‎ ‎2013济南中考 如图1，在△ABC中，AB＝AC＝4，∠ABC＝67.5°，△ABD和△ABC关于AB所在的直线对称，点M为边AC上的一个动点（不与点A，C重合），点M关于AB所在直线的对称点为N，△CMN的面积为S．‎ ‎（1）求∠CAD的度数；‎ ‎（2）设CM＝x，求S与x的函数表达式，并求x为何值时S的值最大？‎ C A M N D B 第27题图1‎ C A M N D B 第27题图2‎ E ‎（3）S的值最大时，过点C作EC⊥AC交AB的延长线于点E，连接EN（如图2）．P为线段EN上一点，Q为平面内一点，当以M，N，P，Q为顶点的四边形是菱形时，请直接写出所有满足条件的NP的长．‎ ‎2014济南中考 如图1，有一组平行线l1∥l2∥l3∥l4，正方形ABCD的第四个顶点分别在l1，l2，l3，l4上，‎ EG过点D且垂直l1于点E，分别交l2，l4于点F1，G1，EF=DG=1，DF=2．‎ ‎（1）AE=　 　，正方形ABCD的边长= 　；‎ ‎（2）如图2，将∠AEG绕点A顺时针旋转得到∠AE′D′，旋转角为α（0°＜α＜90°），点D′在直线l3上，以AD′为边在E′D′左侧作菱形AB′C′D′，使B′，C′分别在直线l2，l4上 ‎①写出∠B′AD′与α的数量关系并给出证明；‎ ‎②若α=30°，求菱形AB′C′D′的边长．‎ ‎2015济南中考 ‎27．（9分）（2015•济南）如图1，在△ABC中，∠ACB=90°，AC=BC，∠EAC=90°，‎ 点M为射线AE上任意一点（不与A重合），连接CM，‎ 将线段CM绕点C按顺时针方向旋转90°得到线段CN，‎ 直线NB分别交直线CM、射线AE于点F、D．‎ ‎（1）直接写出∠NDE的度数；‎ ‎（2）如图2、图3，当∠EAC为锐角或钝角时，其他条件不变，（1）中的结论是否发生变化？‎ 如果不变，选取其中一种情况加以证明；如果变化，请说明理由；‎ ‎（3）如图4，若∠EAC=15°，∠ACM=60°，直线CM与AB交于G，BD= ，‎ 其他条件不变，求线段AM的长．‎ ‎ ‎ 参考答案 ‎2007济南中考 解：（1）∠AOC=900‎ 是的直径， 1分 又点的坐标为，‎ ‎ 2分 ‎， 3分 ‎（2）如图，连接，过点作轴于点 4分 为的切线，‎ ‎， 5分 ‎，，‎ ‎，‎ 在中，‎ ‎ 6分 在中，‎ ‎，‎ 点的坐标为 7分 设过点的反比例函数的表达式为 ‎ 8分 ‎ 9分 ‎2008济南中考 解：（1） 解得： ∴点P的坐标为(2，) ‎ ‎（2）将代入 ∴ ，即OA=4 ‎ 做PD⊥OA于D，则OD=2，PD=2‎ ‎∵ tan∠POA= ∴ ∠POA=60° ‎ F P x O B C E A y ‎∵ OP= ∴△POA是等边三角形． ‎ ‎（3）① 当02，∴当t=时，S最大= ‎ ‎2009济南中考 解：（1）如图①，过、分别作于，于，‎ 则四边形是矩形 ∴-----1分 在中， -----2分 在中，由勾股定理得， ∴------3分 图①）‎ A D C B K H 图②）‎ A D C B G M N ‎（2）如图②，过作交于点，则四边形是平行四边形 ‎∵ ∴‎ ‎∴ ∴-----4分 由题意知，当、运动到秒时，‎ ‎∵ ∴‎ 又 ∴ ∴-----5分 ‎ 即 解得，------6分 A D C B M N 图③）‎ 图④）‎ A D C B M N H E ‎（图⑤）‎ A D C B H N M F ‎（3）分三种情况讨论：‎ ‎①当时，如图③，即 ∴-----7分 ‎②当时，如图④，过作于 解法一：‎ 由等腰三角形三线合一性质得 在中，‎ 又在中， ∴ 解得-----8分 解法二：‎ ‎∵ ∴‎ ‎∴ 即 ∴------8分 ‎③当时，如图⑤，过作于点.‎ 解法一：（方法同②中解法一）‎ ‎ 解得 解法二：‎ ‎∵ ∴‎ ‎∴ 即 ∴‎ 综上所述，当、或时，为等腰三角形-----9分 ‎2010济南中考 解： ⑴证明：∵点M、P、N分别是AB、BC、CA的中点，‎ A B C M N P1‎ 第2题图 P2‎ ‎1‎ ‎2‎ ‎ ∴线段MP、PN是△ABC的中位线，‎ ‎∴MP∥AN，PN∥AM， 1分 ‎ ∴四边形AMPN是平行四边形， 2分 ‎ ∴∠MPN=∠A. 3分 ‎⑵∠MP1N+∠MP2N=∠A正确. 4分 如图所示，连接MN， 5分 ‎∵，∠A=∠A，‎ ‎∴△AMN∽△ABC， ∴∠AMN=∠B，， ‎ ‎∴MN∥BC，MN=BC， 6分 ‎∵点P1、P2是边BC的三等分点，‎ ‎∴MN与BP1平行且相等，MN与P1P2平行且相等，MN与P2C平行且相等，‎ ‎∴四边形MBP1N、MP1P2N、MP2CN都是平行四边形，‎ ‎∴MB∥NP1，MP1∥NP2，MP2∥AC，-----7分 ‎∴∠MP1N=∠1，∠MP2N=∠2，∠BMP2=∠A，‎ ‎∴∠MP1N+∠MP2N=∠1+∠2=∠BMP2=∠A.----8分 ‎⑶∠A. -----9分 ‎2011济南中考 ‎3.解：（1）将A、C两点坐标代入抛物线，图1‎ E ，解得，‎ ‎∴抛物线的解析式为；‎ ‎（2）①∵OA=8，OC=6 ∴，‎ 过点Q作QE⊥BC与E点，则，‎ ‎∴， ∴，‎ ‎∴‎ ‎∴当m=5时，S取最大值；‎ ‎②在抛物线对称轴l上存在点F，使△FDQ为直角三角形，满足条件的点F共有四个，‎ 坐标分别为F1（，4），F2（，8），F3（，），F4（，）．‎ ‎2012济南中考 ‎4解：（1）∵双曲线经过点D（6，1）， ∴，解得k=6；‎ ‎（2）设点C到BD的距离为h，‎ ‎∵点D的坐标为（6，1），DB⊥y轴， ∴BD=6，∴S△BCD=×6•h=12，解得h=4，‎ ‎∵点C是双曲线第三象限上的动点，点D的纵坐标为1， ∴点C的纵坐标为1－4= －3，‎ ‎∴，解得x= －2， ∴点C的坐标为（－2，－3），‎ 设直线CD的解析式为y=kx+b，则，解得，所以，直线CD的解析式为；‎ ‎（3）AB∥CD．理由如下：‎ ‎∵CA⊥x轴，DB⊥y轴，点C的坐标为（－2，－3），点D的坐标为（6，1），‎ ‎∴点A、B的坐标分别为A（－2，0），B（0，1），‎ 设直线AB的解析式为y=mx+n，则，解得， 所以，直线AB的解析式为，‎ ‎∵AB、CD的解析式k都等于相等， ∴AB与CD的位置关系是AB∥CD．‎ ‎2013济南中考 解： (1) ∵AB=AC，∠ABC=67.5° ∴∠ABC=∠ACB=67.5°∴∠CAB=45°‎ ‎∵△ABD和△ABC关于AB所在直线对称∴∠BAD=∠CAB=45°∴∠CAD=90°‎ ‎（2）由（1）可知AN⊥AM ‎ ‎∵点M，N关于AB所在直线对称 ∴AM=AN ‎∵CM=x，∴AN =AM=4-x ∴S==‎ ‎∴S= ∴当x==2时，S有最大值 ‎（3）∵CE⊥AC，∴∠ECA=90°， ∵∠CAB=45°，∴∠CEA=∠EAC=45°，∴CE=AC=4， 在Rt△ECA中，AC=EC=4，由勾股定理得：EA=√42+42=4√2， ∵AM=AN，∠CAB=∠DAB，∴AO⊥MN，MO=NO， 在Rt△MAN中，AM=AN=4-2=2，由勾股定理得：MN=√22+22=2√2，∴MO=NO=√2， 由勾股定理得：AO=√22-(√2)2=√2，∴EO=4√2-√2=3√2， 在Rt△EON中，EO=3√2，MO=√2，由勾股定理得：EM=√(3√2)2+(√2)2=2√5， 分为三种情况：①当以MN为对角线时，此时P在E上，即NP=NE=2√5； ②以MN为一边时，以N为圆心，以MN为半径画弧交NE于P，此时NP=MN=2√2； ③以MN为一边时，过M作MZ⊥NE于Z，则PZ=NZ， ∵AE⊥MN，∴∠EON=∠MZN=90°， ∵∠ENO=∠MNZ，∴△ENO∽△MNZ， ∴‎ ‎∴；；‎ ‎2014济南中考 ‎.解：（1）由题意可得：∠1+∠3=90°，∠1+∠2=90°，∴∠2=∠3，‎ 在△AED和△DGC中，，∴△AED≌△DGC（AAS），∴AE=GD=1，‎ 又∵DE=1+2=3，∴正方形ABCD的边长==， 故答案为：1，；‎ ‎（2）①∠B′AD′=90°﹣α；理由：过点B′作B′M垂直于l1于点M，‎ 在Rt△AED′和Rt△B′MA中，，∴Rt△AED′≌Rt△B′MA（HL），‎ ‎∴∠D′AE+∠B′AM=90°，∠B′AD′+α=90°， ∴∠B′AD′=90°﹣α；‎ ‎②过点E作ON垂直于l1分别交l1，l3于点O，N，‎ 若α=30°，则∠ED′N=60°，AE=1， 故EO=，EN=，ED′=，‎ 由勾股定理可知菱形的边长为：==．‎ 点评：‎ ‎2015济南中考 解：（1）∵∠ACB=90°，∠MCN=90°，∴∠ACM=∠BCN，‎ 在△MAC和△NBC中，，∴△MAC≌△NBC，∴∠NBC=∠MAC=90°，‎ 又∵∠ACB=90°，∠EAC=90°，∴∠NDE=90°；‎ ‎（2）不变，‎ 在△MAC≌△NBC中，，∴△MAC≌△NBC，∴∠N=∠AMC，‎ 又∵∠MFD=∠NFC，∠MDF=∠FCN=90°，即∠NDE=90°；‎ ‎（3）作GK⊥BC于K，‎ ‎∵∠EAC=15°，∴∠BAD=30°，‎ ‎∵∠ACM=60°，∴∠GCB=30°，‎ ‎∴∠AGC=∠ABC+∠GCB=75°，‎ ‎∠AMG=75°，∴AM=AG，‎ ‎∵△MAC≌△NBC，∴∠MAC=∠NBC，∴∠BDA=∠BCA=90°，‎ ‎∵BD=，∴AB=+，‎ AC=BC=+1，‎ 设BK=a，则GK=a，CK=a，‎ ‎∴a+a=+1，∴a=1，‎ ‎∴KB=KG=1，BG=，‎ AG=，‎ ‎∴AM=．‎