中考数学压轴题精选测试题 15页

全国中考数学压轴题精选1‎ ‎1.（08福建莆田）26．（14分）如图：抛物线经过A（-3，0）、B（0，4）、C（4，0）三点.‎ ‎ （1） 求抛物线的解析式.‎ ‎ （2）已知AD = AB（D在线段AC上），有一动点P从点A沿线段AC以每秒1个单位长度的速度移动；同时另一个动点Q以某一速度从点B沿线段BC移动，经过t 秒的移动，线段PQ被BD垂直平分，求t的值；‎ ‎ （3）在（2）的情况下，抛物线的对称轴上是否存在一点M，使MQ+MC的值最小？若存在，请求出点M的坐标；若不存在，请说明理由。‎ ‎（注：抛物线的对称轴为）‎ ‎（08福建莆田26题解析）26（1）解法一：设抛物线的解析式为y = a (x +3 )(x - 4)‎ ‎ 因为B（0，4）在抛物线上，所以4 = a ( 0 + 3 ) ( 0 - 4 )解得a= -1/3‎ ‎ 所以抛物线解析式为 解法二：设抛物线的解析式为，‎ 依题意得：c=4且 解得 ‎ 所以 所求的抛物线的解析式为 ‎（2）连接DQ，在Rt△AOB中，‎ 所以AD=AB= 5，AC=AD+CD=3 + 4 = 7，CD = AC - AD = 7 – 5 = 2‎ 因为BD垂直平分PQ，所以PD=QD，PQ⊥BD，所以∠PDB=∠QDB 因为AD=AB，所以∠ABD=∠ADB，∠ABD=∠QDB，所以DQ∥AB 所以∠CQD=∠CBA。∠CDQ=∠CAB，所以△CDQ∽ △CAB ‎ 即 所以AP=AD – DP = AD – DQ=5 –= ， ‎ 所以t的值是 ‎（3）答对称轴上存在一点M，使MQ+MC的值最小 理由：因为抛物线的对称轴为 所以A（- 3，0），C（4，0）两点关于直线对称 连接AQ交直线于点M，则MQ+MC的值最小 过点Q作QE⊥x轴，于E，所以∠QED=∠BOA=900‎ ‎ DQ∥AB，∠ BAO=∠QDE， △DQE ∽△ABO ‎ 即 ‎ 所以QE=，DE=，所以OE = OD + DE=2+=，所以Q（，）‎ 设直线AQ的解析式为 则 由此得 ‎ 所以直线AQ的解析式为 联立 由此得 所以M 则：在对称轴上存在点M，使MQ+MC的值最小。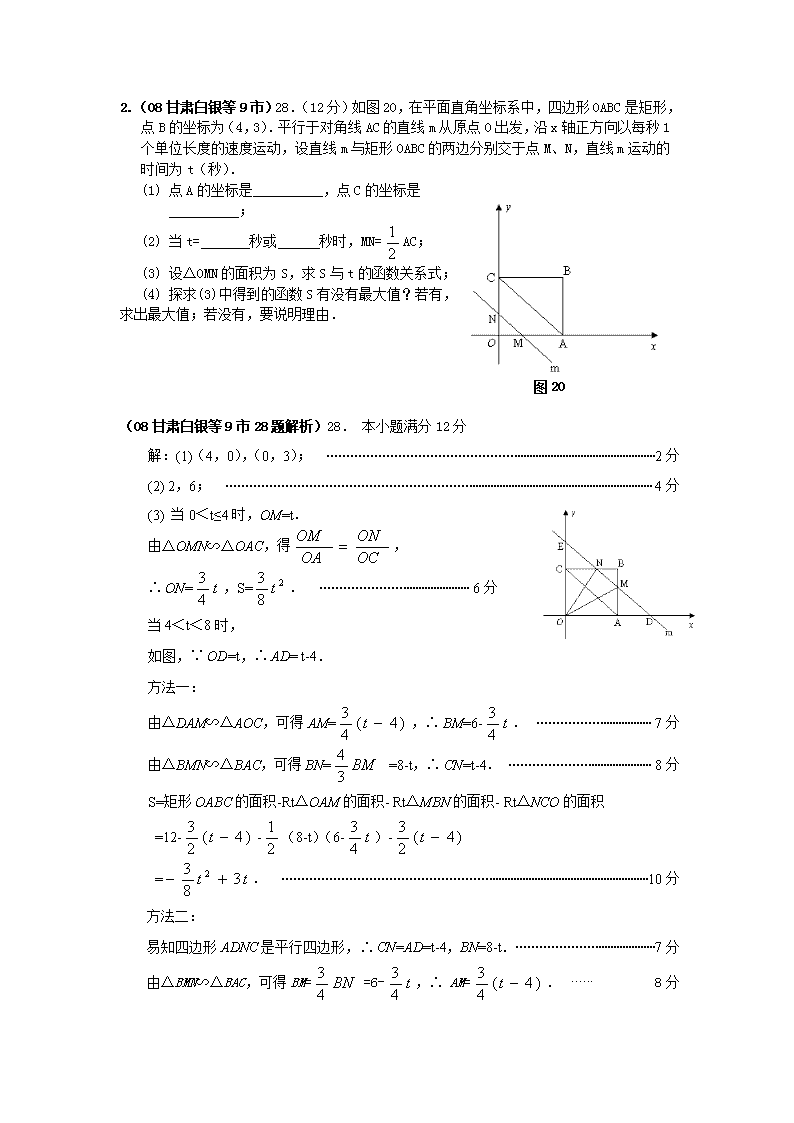‎ ‎2.（08甘肃白银等9市）28．（12分）如图20，在平面直角坐标系中，四边形OABC是矩形，点B的坐标为（4，3）．平行于对角线AC的直线m从原点O出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线m与矩形OABC的两边分别交于点M、N，直线m运动的时间为t（秒）．‎ 图20‎ ‎(1) 点A的坐标是__________，点C的坐标是__________；‎ ‎ (2) 当t= 秒或 秒时，MN=AC；‎ ‎(3) 设△OMN的面积为S，求S与t的函数关系式；‎ ‎(4) 探求(3)中得到的函数S有没有最大值？若有，求出最大值；若没有，要说明理由．‎ ‎（08甘肃白银等9市28题解析）28． 本小题满分12分 解：(1)（4，0），（0，3）； 2分 ‎(2) 2，6； 4分 ‎(3) 当0＜t≤4时，OM=t．‎ 由△OMN∽△OAC，得，‎ ‎∴ ON=，S=． 6分 当4＜t＜8时，‎ 如图，∵ OD=t，∴ AD= t-4． ‎ 方法一：‎ 由△DAM∽△AOC，可得AM=，∴ BM=6-． 7分 由△BMN∽△BAC，可得BN==8-t，∴ CN=t-4． 8分 S=矩形OABC的面积-Rt△OAM的面积- Rt△MBN的面积- Rt△NCO的面积 ‎=12--（8-t）（6-）-‎ ‎=． 10分 方法二：‎ 易知四边形ADNC是平行四边形，∴ CN=AD=t-4，BN=8-t． 7分 由△BMN∽△BAC，可得BM==6-，∴ AM=． 8分 以下同方法一．‎ ‎ (4) 有最大值．‎ 方法一：‎ 当0＜t≤4时，‎ ‎∵ 抛物线S=的开口向上，在对称轴t=0的右边， S随t的增大而增大，‎ ‎∴ 当t=4时，S可取到最大值=6； 11分 当4＜t＜8时，‎ ‎∵ 抛物线S=的开口向下，它的顶点是（4，6），∴ S＜6． ‎ 综上，当t=4时，S有最大值6． 12分 方法二：‎ ‎∵ S= ‎ ‎∴ 当0＜t＜8时，画出S与t的函数关系图像，如图所示． 11分 显然，当t=4时，S有最大值6． 12分 说明：只有当第（3）问解答正确时，第（4）问只回答“有最大值”无其它步骤，可给1分；否则，不给分．‎ ‎3.（08广东广州）25、（2008广州）（14分）如图11，在梯形ABCD中，AD∥BC，AB=AD=DC=‎2cm，BC=‎4cm，在等腰△PQR中，∠QPR=120°，底边QR=‎6cm，点B、C、Q、R在同一直线l上，且C、Q两点重合，如果等腰△PQR以‎1cm/秒的速度沿直线l箭头所示方向匀速运动，t秒时梯形ABCD与等腰△PQR重合部分的面积记为S平方厘米 ‎（1）当t=4时，求S的值 ‎（2）当，求S与t的函数关系式，并求出S的最大值 图11‎ ‎（08广东广州25题解析）25．（1）t＝4时,Q与B重合，P与D重合，‎ 重合部分是＝‎ ‎4.（08广东深圳）22．如图9，在平面直角坐标系中，二次函数的图象的顶点为D点，与y轴交于C点，与x轴交于A、B两点， A点在原点的左侧，B点的坐标为（3，0），‎ OB＝OC ，tan∠ACO＝．‎ ‎（1）求这个二次函数的表达式．‎ ‎（2）经过C、D两点的直线，与x轴交于点E，在该抛物线上是否存在这样的点F，使以点A、C、E、F为顶点的四边形为平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由．‎ ‎（3）若平行于x轴的直线与该抛物线交于M、N两点，且以MN为直径的圆与x轴相切，求该圆半径的长度．‎ ‎（4）如图10，若点G（2，y）是该抛物线上一点，点P是直线AG下方的抛物线上一动点，当点P运动到什么位置时，△APG的面积最大？求出此时P点的坐标和△APG的最大面积.‎ ‎ ‎ ‎（08广东深圳22题解析）22．（1）方法一：由已知得：C（0，－3），A（－1，0） …1分 将A、B、C三点的坐标代入得 ……………………2分 解得： ……………………3分 所以这个二次函数的表达式为： ……………………3分 方法二：由已知得：C（0，－3），A（－1，0） ………………………1分 设该表达式为： ……………………2分 将C点的坐标代入得： ……………………3分 所以这个二次函数的表达式为： ……………………3分 ‎（注：表达式的最终结果用三种形式中的任一种都不扣分）‎ ‎（2）方法一：存在，F点的坐标为（2，－3） ……………………4分 理由：易得D（1，－4），所以直线CD的解析式为：‎ ‎∴E点的坐标为（－3，0） ……………………4分 由A、C、E、F四点的坐标得：AE＝CF＝2，AE∥CF ‎∴以A、C、E、F为顶点的四边形为平行四边形 ‎∴存在点F，坐标为（2，－3） ……………………5分 方法二：易得D（1，－4），所以直线CD的解析式为：‎ ‎∴E点的坐标为（－3，0） ………………………4分 ‎∵以A、C、E、F为顶点的四边形为平行四边形 ‎∴F点的坐标为（2，－3）或（―2，―3）或（－4，3） ‎ 代入抛物线的表达式检验，只有（2，－3）符合 ‎∴存在点F，坐标为（2，－3） ………………………5分 ‎（3）如图，①当直线MN在x轴上方时，设圆的半径为R（R>0），则N（R+1，R），‎ 代入抛物线的表达式，解得 …………6分 ‎②当直线MN在x轴下方时，设圆的半径为r（r>0），‎ 则N（r+1，－r），‎ 代入抛物线的表达式，解得 ………7分 ‎∴圆的半径为或． ……………7分 ‎（4）过点P作y轴的平行线与AG交于点Q，‎ 易得G（2，－3），直线AG为．……………8分 设P（x，），则Q（x，－x－1），PQ．‎ ‎ ……………………9分 当时，△APG的面积最大 此时P点的坐标为，． ……………………10分 ‎5.（08贵州贵阳）25．（本题满分12分）(本题暂无答案)‎ 某宾馆客房部有60个房间供游客居住，当每个房间的定价为每天200元时，房间可以住满．当每个房间每天的定价每增加10元时，就会有一个房间空闲．对有游客入住的房间，宾馆需对每个房间每天支出20元的各种费用．‎ 设每个房间每天的定价增加元．求：‎ ‎（1）房间每天的入住量（间）关于（元）的函数关系式．（3分）‎ ‎（2）该宾馆每天的房间收费（元）关于（元）的函数关系式．（3分）‎ ‎（3）该宾馆客房部每天的利润（元）关于（元）的函数关系式；当每个房间的定价为每天多少元时，有最大值？最大值是多少？（6分）‎ ‎6.（08湖北恩施）六、(本大题满分12分)‎ ‎24. 如图11，在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起，A 为公共顶点，∠BAC=∠AGF=90°，它们的斜边长为2，若∆ABC固定不动，∆AFG绕点A旋转，AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m，CD=n.‎ ‎（1）请在图中找出两对相似而不全等的三角形，并选取其中一对进行证明.‎ ‎（2）求m与n的函数关系式，直接写出自变量n的取值范围.‎ ‎ （3）以∆ABC的斜边BC所在的直线为x轴，BC边上的高所在的直线为y轴，建立平面直角坐标系(如图12).在边BC上找一点D，使BD=CE，求出D点的坐标，并通过计算验证BD＋CE=DE.‎ G y x 图12‎ O F E D C B A G 图11‎ F E D C B A ‎ （4）在旋转过程中,(3)中的等量关系BD＋CE=DE是否始终成立,若成立,请证明,若不成立,请说明理由.‎ ‎ ‎ ‎ ‎ ‎（08湖北恩施24题解析）六、(本大题满分12分)‎ ‎24. 解:(1)∆ABE∽∆DAE, ∆ABE∽∆DCA 1分 ‎ ∵∠BAE=∠BAD+45°,∠CDA=∠BAD+45°‎ ‎ ∴∠BAE=∠CDA ‎ 又∠B=∠C=45°‎ ‎ ∴∆ABE∽∆DCA 3分 ‎ (2)∵∆ABE∽∆DCA ‎ ∴‎ ‎ 由依题意可知CA=BA=‎ ‎ ∴‎ ‎ ∴m= 5分 ‎ 自变量n的取值范围为1