中考数学专题压轴题内含答案 12页

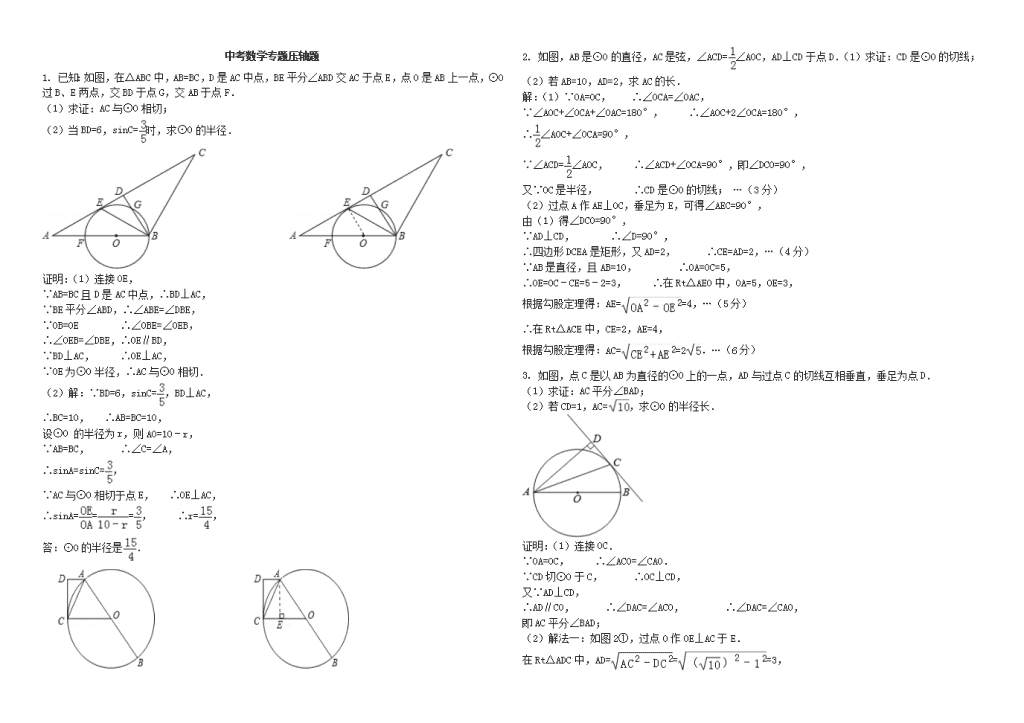
中考数学专题压轴题 ‎1. 已知：如图，在△ABC中，AB=BC，D是AC中点，BE平分∠ABD交AC于点E，点O是AB上一点，⊙O过B、E两点，交BD于点G，交AB于点F．‎ ‎（1）求证：AC与⊙O相切；‎ ‎（2）当BD=6，sinC=时，求⊙O的半径．‎ ‎ ‎ 证明：（1）连接OE，‎ ‎∵AB=BC且D是AC中点，∴BD⊥AC，‎ ‎∵BE平分∠ABD，∴∠ABE=∠DBE，‎ ‎∵OB=OE ∴∠OBE=∠OEB，‎ ‎∴∠OEB=∠DBE，∴OE∥BD，‎ ‎∵BD⊥AC， ∴OE⊥AC，‎ ‎∵OE为⊙O半径，∴AC与⊙O相切．‎ ‎（2）解：∵BD=6，sinC=，BD⊥AC，‎ ‎∴BC=10， ∴AB=BC=10，‎ 设⊙O 的半径为r，则AO=10﹣r，‎ ‎∵AB=BC， ∴∠C=∠A，‎ ‎∴sinA=sinC=，‎ ‎∵AC与⊙O相切于点E， ∴OE⊥AC，‎ ‎∴sinA===， ∴r=，‎ 答：⊙O的半径是．‎ ‎ ‎ ‎2. 如图，AB是⊙O的直径，AC是弦，∠ACD=∠AOC，AD⊥CD于点D．（1）求证：CD是⊙O的切线；（2）若AB=10，AD=2，求AC的长．‎ 解：（1）∵OA=OC， ∴∠OCA=∠OAC，‎ ‎∵∠AOC+∠OCA+∠OAC=180°， ∴∠AOC+2∠OCA=180°，‎ ‎∴∠AOC+∠OCA=90°，‎ ‎∵∠ACD=∠AOC， ∴∠ACD+∠OCA=90°，即∠DCO=90°，‎ 又∵OC是半径， ∴CD是⊙O的切线； …（3分）‎ ‎（2）过点A作AE⊥OC，垂足为E，可得∠AEC=90°，‎ 由（1）得∠DCO=90°，‎ ‎∵AD⊥CD， ∴∠D=90°，‎ ‎∴四边形DCEA是矩形，又AD=2， ∴CE=AD=2，…（4分）‎ ‎∵AB是直径，且AB=10， ∴OA=OC=5，‎ ‎∴OE=OC﹣CE=5﹣2=3， ∴在Rt△AEO中，OA=5，OE=3，‎ 根据勾股定理得：AE==4，…（5分）‎ ‎∴在Rt△ACE中，CE=2，AE=4，‎ 根据勾股定理得：AC==2．…（6分）‎ ‎3. 如图，点C是以AB为直径的⊙O上的一点，AD与过点C的切线互相垂直，垂足为点D．‎ ‎（1）求证：AC平分∠BAD；‎ ‎（2）若CD=1，AC=，求⊙O的半径长．‎ 证明：（1）连接OC．‎ ‎∵OA=OC， ∴∠ACO=∠CAO．‎ ‎∵CD切⊙O于C， ∴OC⊥CD，‎ 又∵AD⊥CD，‎ ‎∴AD∥CO， ∴∠DAC=∠ACO， ∴∠DAC=∠CAO，‎ 即AC平分∠BAD；‎ ‎（2）解法一：如图2①，过点O作OE⊥AC于E．‎ 在Rt△ADC中，AD===3，‎ ‎∵OE⊥AC， ∴AE=AC=．‎ ‎∵∠CAO=∠DAC，∠AEO=∠ADC=90°， ∴△AEO∽△ADC，‎ ‎∴，即， ∴AO=，即⊙O的半径为．‎ 解法二：如图2②，连接BC．‎ 在Rt△ADC中，AD===3．‎ ‎∵AB是⊙O直径，∴∠ACB=90°，‎ ‎∵∠CAB=∠DAC，∠ACB=∠ADC=90°， ∴△ABC∽△ACD，‎ ‎∴， 即，‎ ‎∴AB=， ∴=， 即⊙O的半径为．‎ ‎4. 如图，⊙O的直径AB=10，C、D是圆上的两点，且．设过点D的切线ED交AC的延长线于点F．连接OC交AD于点G．‎ ‎（1）求证：DF⊥AF．‎ ‎（2）求OG的长．‎ ‎ ‎ 解：（1）连接OD，则OD⊥EF，‎ ‎∵， ∴∠CAD=∠DAB=30°，‎ ‎∵AO=DO， ∴∠OAD=∠ADO，‎ ‎∴∠FAD=∠ADO， ∴AF∥DO，‎ ‎∴DF⊥AF．‎ ‎（2）在Rt△ABD中，∠BAD=30°，AB=10，‎ ‎∴BD=5，‎ ‎∵=， ∴OG垂直平分AD， ∴OG是△ABD的中位线，‎ ‎∴OG=BD=．‎ ‎5. 已知：⊙O的直径为3，线段AC=4，直线AC和PM分别与⊙O相切于点A，M．‎ ‎（1）求证：点P是线段AC的中点；‎ ‎（2）求sin∠PMC的值．‎ ‎ ‎ 证明：（1）连结OM，如图，‎ ‎∵直线AC和PM分别与⊙O相切于点A，M， ∴PM=PA，OM⊥MP，BA⊥AC，‎ ‎∴∠OMP=90°，∠BAC=90°， ∴∠1+∠2=90°，∠B+∠C=90°，‎ 而∠2=∠B，‎ ‎∴∠1=∠C，∴PC=PM，∴PA=PC， ∴点P是线段AC的中点；‎ ‎（2）解：由（1）∠PMC=∠C，‎ 在Rt△ABC中，AB=3，AC=4，‎ ‎∴BC==5，∴sin∠C==，‎ 即sin∠PMC=．‎ ‎ 6.如图，在△ABC中，AB=AC，以AB为直径作半圆⊙O，交BC于点D，连接AD，过点D作DE⊥AC，垂足为点E，交AB的延长线于点F．‎ ‎（1）求证：EF是⊙0的切线．（2）如果⊙0的半径为5，sin∠ADE=，求BF的长．‎ ‎ ‎ 证明：（1）连接OD，如图，‎ ‎∵AB为⊙0的直径， ∴∠ADB=90°，‎ ‎∴AD⊥BC，‎ ‎∵AB=AC， ∴AD平分BC，即DB=DC，‎ ‎∵OA=OB， ∴OD为△ABC的中位线，‎ ‎∴OD∥AC，‎ ‎∵DE⊥AC， ∴OD⊥DE，‎ ‎∴EF是⊙0的切线；‎ ‎（2）解：∵∠DAC=∠DAB， ∴∠ADE=∠ABD，‎ 在Rt△ADB中，sin∠ADE=sin∠ABD==，而AB=10， ∴AD=8，‎ 在Rt△ADE中，sin∠ADE==， ∴AE=，‎ ‎∵OD∥AE，‎ ‎∴△FDO∽△FEA， ∴=， 即=，‎ ‎∴BF=．‎ ‎7.如图，AB是⊙O的直径，∠B=∠CAD．‎ ‎（1）求证：AC是⊙O的切线；‎ ‎（2）若点E是的中点，连接AE交BC于点F，当BD=5，CD=4时，求AF的值．‎ 解：（1）∵AB是⊙O的直径，‎ ‎∴∠ADB=∠ADC=90°，‎ ‎∵∠B=∠CAD，∠C=∠C， ∴△ADC∽△BAC，‎ ‎∴∠BAC=∠ADC=90°， ∴BA⊥AC，‎ ‎∴AC是⊙O的切线．‎ ‎（2）∵BD=5，CD=4， ∴BC=9，‎ ‎∵△ADC∽△BAC（已证），‎ ‎∴=，即AC2=BC×CD=36，‎ 解得：AC=6，‎ 在Rt△ACD中，AD==2，‎ ‎∵∠CAF=∠CAD+∠DAE=∠ABF+∠BAE=∠AFD， ∴CA=CF=6，‎ ‎∴DF=CA﹣CD=2，‎ 在Rt△AFD中，AF==2．‎ ‎8. 如图，△ABC中，以AB为直径的⊙O交AC于点D，∠DBC=∠BAC．‎ ‎（1）求证：BC是⊙O的切线；‎ ‎（2）若⊙O的半径为2，∠BAC=30°，求图中阴影部分的面积．‎ 证明：（1）∵AB为⊙O直径，‎ ‎∴∠ADB=90°， ∴∠BAC+∠ABD=90°，‎ ‎∵∠DBC=∠BAC， ∴∠DBC+∠ABD=90°，‎ ‎∴AB⊥BC，‎ ‎∵AB为直径， ∴BC是⊙O切线；‎ ‎（2）解：连接OD，过O作OM⊥BD于M，‎ ‎∵∠BAC=30°， ∴∠BOD=2∠A=60°，‎ ‎∵OB=OD， ∴△OBD是等边三角形，‎ ‎∴OB=BD=OD=2， ∴BM=DM=1，‎ 由勾股定理得：OM=，‎ ‎∴阴影部分的面积S=S扇形DOB﹣S△DOB=﹣×2×=π﹣．‎ ‎9. 如图，在△ABC中，∠BAC=90°，AB=AC，AB是⊙O的直径，⊙O交BC于点D，DE⊥AC于点E，BE交⊙O于点F，连接AF，AF的延长线交DE于点P．‎ ‎（1）求证：DE是⊙O的切线；‎ ‎（2）求tan∠ABE的值；‎ ‎（3）若OA=2，求线段AP的长．‎ ‎ ‎ 证明：（1）连接AD、OD，如图，‎ ‎∵AB是⊙O的直径，∴∠ADB=90°，‎ ‎∵AB=AC，∴AD垂直平分BC，即DC=DB，‎ ‎∴OD为△BAC的中位线，∴OD∥AC，‎ 而DE⊥AC，‎ ‎∴OD⊥DE，∴DE是⊙O的切线；‎ ‎（2）解：∵OD⊥DE，DE⊥AC，‎ ‎∴四边形OAED为矩形，‎ 而OD=OA，‎ ‎∴四边形OAED为正方形，∴AE=AO，‎ ‎∴tan∠ABE==；‎ ‎（3）解：∵AB是⊙O的直径， ∴∠AFB=90°，‎ ‎∴∠ABF+∠FAB=90°，‎ 而∠EAP+∠FAB=90°，‎ ‎∴∠EAP=∠ABF，‎ ‎∴tan∠EAP=tan∠ABE=，‎ 在Rt△EAP中，AE=2，‎ ‎∵tan∠EAP==， ∴EP=1，‎ ‎∴AP==．‎ ‎10.如图，Rt△ABC中，∠ABC=90°，以AB为直径作半圆⊙O交AC与点D，点E为BC的中点，连接DE．‎ ‎（1）求证：DE是半圆⊙O的切线．‎ ‎（2）若∠BAC=30°，DE=2，求AD的长．‎ ‎ ‎ 证明：（1）连接OD，OE，‎ ‎∵AB为圆O的直径， ∴∠ADB=∠BDC=90°，‎ 在Rt△BDC中，E为斜边BC的中点，‎ ‎∴DE=BE，‎ 在△OBE和△ODE中，‎ ‎，‎ ‎∴△OBE≌△ODE（SSS）， ∴∠ODE=∠ABC=90°，‎ 则DE为圆O的切线；‎ ‎（2）在Rt△ABC中，∠BAC=30°，‎ ‎∴BC=AC， ∵BC=2DE=4，‎ ‎∴AC=8，‎ 又∵∠C=60°，DE=DC，‎ ‎∴△DEC为等边三角形，即DC=DE=2，‎ 则AD=AC﹣DC=6．‎ ‎11. 如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．‎ ‎（1）BD与CD有什么数量关系，并说明理由；‎ ‎（2）当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．‎ ‎ ‎ 解：（1）BD=CD．‎ 理由如下：∵AF∥BC， ∴∠AFE=∠DCE，‎ ‎∵E是AD的中点，‎ ‎∴AE=DE，‎ 在△AEF和△DEC中，，‎ ‎∴△AEF≌△DEC（AAS）， ∴AF=CD，‎ ‎∵AF=BD， ∴BD=CD；‎ ‎（2）当△ABC满足：AB=AC时，四边形AFBD是矩形．‎ 理由如下：∵AF∥BD，AF=BD，[来源:学*科*网Z*X*X*K]‎ ‎∴四边形AFBD是平行四边形，‎ ‎∵AB=AC，BD=CD， ∴∠ADB=90°，‎ ‎∴▱AFBD是矩形．‎ ‎12. （一定要看会）已知抛物线的方程C1： (m＞0)与x轴交于点B、C，与y轴交于点E，且点B在点C的左侧．‎ ‎（1）若抛物线C1过点M(2, 2)，求实数m的值；‎ ‎（2）在（1）的条件下，求△BCE的面积；‎ ‎（3）在（1）的条件下，在抛物线的对称轴上找一点H，使得BH＋EH最小，求出点H的坐标；‎ ‎（4）在第四象限内，抛物线C1上是否存在点F，使得以点B、C、F为顶点的三角形与△BCE相似？若存在，求m的值；若不存在，请说明理由．‎ 解：（1）将M(2, 2)代入，得．解得m＝4．‎ ‎（2）当m＝4时，．所以C(4, 0)，E(0, 2)．‎ 所以S△BCE＝．‎ ‎（3）如图2，抛物线的对称轴是直线x＝1，当H落在线段EC上时，BH＋EH最小．‎ 设对称轴与x轴的交点为P，那么．‎ 因此．解得．所以点H的坐标为．‎ ‎（4）①如图3，过点B作EC的平行线交抛物线于F，过点F作FF′⊥x轴于F′．‎ 由于∠BCE＝∠FBC，所以当，即时，△BCE∽△FBC．‎ 设点F的坐标为，由，得．‎ 解得x＝m＋2．所以F′(m＋2, 0)．‎ 由，得．所以．‎ 由，得．‎ 整理，得0＝16．此方程无解．‎ 图2 图3 图4‎ ‎②如图4，作∠CBF＝45°交抛物线于F，过点F作FF′⊥x轴于F′，‎ 由于∠EBC＝∠CBF，所以，即时，△BCE∽△BFC．‎ 在Rt△BFF′中，由FF′＝BF′，得．‎ 解得x＝2m．所以F′．所以BF′＝2m＋2，．‎ 由，得．解得．‎ 综合①、②，符合题意的m为．‎ ‎13.已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A（-1，0）、B（0，3）两点，其顶点为D.‎ （1） 求该抛物线的解析式；‎ （2） 若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积；‎ （3） ‎△AOB与△BDE是否相似？如果相似，请予以证明；如果不相似，请说明理由.（注：抛物线y=ax2+bx+c(a≠0)的顶点坐标为）‎ 解：（1）由已知得：解得 c=3,b=2‎ ‎∴抛物线的线的解析式为 ‎(2)由顶点坐标公式得顶点坐标为（1，4）‎ 所以对称轴为x=1,A,E关于x=1对称，所以E(3,0)‎ 设对称轴与x轴的交点为F 所以四边形ABDE的面积=‎ ‎=‎ ‎=‎ ‎=9‎ ‎（3）相似 如图，BD=‎ BE=‎ DE=‎ 所以, 即： ,所以是直角三角形 所以,且,‎ 所以.‎ ‎14.如图，在平面直角坐标系中，直线与轴交于点，与轴交于点，抛物线经过三点．‎ ‎（1）求过三点抛物线的解析式并求出顶点的坐标；‎ ‎（2）在抛物线上是否存在点，使为直角三角形，若存在，直接写出点坐标；若不存在，请说明理由；‎ ‎（3）试探究在直线上是否存在一点，使得的周长最小，若存在，求出点的坐标；若不存在，请说明理由．‎ A O x y B F C H M G A O x y B F C 解：过点作的垂线交轴于点，则点为点关于直线的对称点．连接交于点，则点即为所求． 11分 过点作轴于点，则，．‎ ‎，‎ 同方法一可求得．‎ 在中，，，可求得，‎ 为线段的垂直平分线，可证得为等边三角形，‎ 垂直平分．‎ 即点为点关于的对称点． 12分 设直线的解析式为，由题意得 ‎ 解得 ‎ 13分 ‎ 解得 ‎ 在直线上存在点，使得的周长最小，此时． ‎ ‎15. 已知：如图14，抛物线与轴交于点，点，与直线相交于点，点，直线与轴交于点．‎ ‎（1）写出直线的解析式．‎ ‎（2）求的面积．‎ ‎（3）若点在线段上以每秒1个单位长度的速度从向运动（不与重合），同时，点在射线上以每秒2个单位长度的速度从向运动．设运动时间为秒，请写出的面积与的函数关系式，并求出点运动多少时间时，的面积最大，最大面积是多少？‎ x y A B C E M D P N O 解：（1）在中，令 ‎，‎ ‎， 1分 又点在上 的解析式为 2分 ‎（2）由，得 4分 ‎，‎ ‎， 5分 ‎ 6分 ‎（3）过点作于点 ‎ 7分 ‎ 8分 由直线可得：‎ 在中，，，则 ‎， 9分 ‎ 10分 ‎ 11分 此抛物线开口向下，当时，‎ 当点运动2秒时，的面积达到最大，最大为． ‎ ‎16. 已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A（-1，0）、B（0，3）两点，其顶点为D.‎ ‎(1)求该抛物线的解析式；‎ ‎(2)若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积；‎ ‎(3)△AOB与△BDE是否相似？如果相似，请予以证明；如果不相似，请说明理由.‎ ‎（注：抛物线y=ax2+bx+c(a≠0)的顶点坐标为）‎ 解：（ 1）由已知得：解得 c=3,b=2‎ ‎∴抛物线的线的解析式为 ‎(2)由顶点坐标公式得顶点坐标为（1，4）‎ 所以对称轴为x=1,A,E关于x=1对称，所以E(3,0)‎ 设对称轴与x轴的交点为F 所以四边形ABDE的面积=‎ ‎=‎ ‎=‎ ‎=9‎ ‎（3）相似 如图，BD=‎ BE=‎ DE=‎ 所以, 即： ,所以是直角三角形 所以,且,‎ 所以.‎ ‎17. （2014.临夏州）如图14（1），抛物线与x轴交于A、B两点，与y轴交于点C（0，）．［图14（2）、图14（3）为解答备用图］‎ ‎（1）　　　　　，点A的坐标为　　　　　　，点B的坐标为　　　　　；‎ ‎（2）设抛物线的顶点为M，求四边形ABMC的面积；‎ ‎（3）在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由。‎ ‎ 图14（2）‎ 解：（1）， 1分 A（-1，0）， 2分 B（3，0）． 3分 ‎（2）如图14（1），抛物线的顶点为M（1，-4），连结OM．‎ ‎ 4分 则 △AOC的面积=，△MOC的面积=，‎ ‎△MOB的面积=6， 6分 ‎∴ 四边形 ABMC的面积 ‎=△AOC的面积+△MOC的面积+△MOB的面积=9． 7分 说明：也可过点M作抛物线的对称轴，将四边形ABMC的面 积转化为求1个梯形与2个直角三角形面积的和．‎ ‎（3）如图14（2），设D（m，），连结OD．‎ 则 0＜m＜3， ＜0． ‎ 且 △AOC的面积=，△DOC的面积=， ‎ ‎△DOB的面积=-（）， 9分 ‎∴ 四边形 ABDC的面积=△AOC的面积+△DOC的面积+△DOB的面积 ‎=‎ ‎=． 11分 ‎∴ 存在点D，使四边形ABDC的面积最大为． 12分 ‎18. （2014.白银）如图，在直角坐标系xOy中，二次函数y=x2+（2k﹣1）x+k+1的图象与x轴相交于O、A两点．‎ ‎（1）求这个二次函数的解析式；‎ ‎（2）在这条抛物线的对称轴右边的图象上有一点B，使△AOB的面积等于6，求点B的坐标；‎ ‎（3）对于（2）中的点B，在此抛物线上是否存在点P，使∠POB=90°？若存在，求出点P的坐标，并求出△POB的面积；若不存在，请说明理由．‎ ‎ ‎ 解：①∵函数的图象与x轴相交于O，‎ ‎∴0=k+1，∴k=﹣1，‎ ‎∴y=x2﹣3x，‎ ‎②假设存在点B，过点B做BD⊥x轴于点D，‎ ‎∵△AOB的面积等于6，∴AO•BD=6，‎ 当0=x2﹣3x，‎ x（x﹣3）=0，解得：x=0或3，‎ ‎∴AO=3，∴BD=4‎ ‎ 即4=x2﹣3x，‎ ‎ 解得：x=4或x=﹣1（舍去）．‎ 又∵顶点坐标为：（ 1.5，﹣2.25）．‎ ‎∵2.25＜4，∴x轴下方不存在B点，‎ ‎∴点B的坐标为：（4，4）；‎ ‎③∵点B的坐标为：（4，4），‎ ‎∴∠BOD=45°，BO==4，‎ 当∠POB=90°，‎ ‎∴∠POD=45°，‎ 设P点横坐标为：﹣x，则纵坐标为：x2﹣3x，‎ 即﹣x=x2﹣3x，‎ 解得x=2 或x=0，‎ ‎∴在抛物线上仅存在一点P （2，﹣2）．‎ ‎∴OP==2，‎ 使∠POB=90°，‎ ‎∴△POB的面积为： PO•BO=×4×2=8．‎ ‎19. 如图，在平面直角坐标系中，以点C（1，1）为圆心，2为半径作圆，交x轴于A，B两点，开口向下的抛物线经过点A，B，且其顶点P在⊙C上．‎ ‎（1）求∠ACB的大小；‎ ‎（2）写出A，B两点的坐标；‎ ‎（3）试确定此抛物线的解析式；‎ ‎（4）在该抛物线上是否存在一点D，使线段OP与CD互相平分？若存在，求出点D的坐标；若不存在，请说明理由．‎ ‎ ‎ 解：（1）作CH⊥x轴，H为垂足，‎ ‎∵CH=1，半径CB=2，‎ ‎∵∠BCH=60°，‎ ‎∴∠ACB=120°．‎ ‎（2）∵CH=1，半径CB=2‎ ‎∴HB=，故A（1﹣，0），‎ B（1+，0）．‎ ‎（3）由圆与抛物线的对称性可知抛物线的顶点P的坐标为（1，3）‎ 设抛物线解析式y=a（x﹣1）2+3，‎ 把点B（1+，0）代入上式，解得a=﹣1；‎ ‎∴y=﹣x2+2x+2．‎ ‎（4）假设存在点D使线段OP与CD互相平分，则四边形OCPD是平行四边形 ‎∴PC∥OD且PC=OD．‎ ‎∵PC∥y轴，‎ ‎∴点D在y轴上．‎ 又∵PC=2，‎ ‎∴OD=2，即D（0，2）．‎ 又D（0，2）满足y=﹣x2+2x+2，‎ ‎∴点D在抛物线上 所以存在D（0，2）使线段OP与CD互相平分．‎ ‎20. 已知二次函数y=﹣x2+（k+1）x﹣k的图象经过一次函数y=﹣x+4的图象与x轴的交点A．（如图）‎ ‎（1）求二次函数的解析式；‎ ‎（2）求一次函数与二次函数图象的另一个交点B的坐标；‎ ‎（3）若二次函数图象与y轴交于点D，平行于y轴的直线l将四边形ABCD的面积分成1：2的两部分，则直线l截四边形ABCD所得的线段的长是多少？（直接写出结果）‎ 解：（1）由y=﹣x+4，得A（4，0），‎ 又二次函数图象经过点A，‎ 则0=﹣16+4（k+1）﹣k，‎ 解得k=4，‎ 所以二次函数解析式为y=﹣x2+5x﹣4．‎ ‎（2）由，‎ 解得，，‎ 所以点B的坐标为（2，2）．‎ ‎（3）令y=0代入二次函数得x=1或x=4，‎ 则C点坐标为（1，0）‎ 令x=0代入2此函数得y=﹣4，则D点坐标为（0，﹣4）‎ ‎∴四边形面积为：×（4﹣1）×2+×（4﹣1）×4=9，‎ ‎①若直线在点B的左侧，‎ 令平行于y轴的直线交BC于E，交CA于F，交AD于G，‎ 求得BC的函数为y=2x﹣2‎ 则=，‎ 同理求得AD的函数为y=x﹣4，∴AF=FG，‎ 设CF=a＞0，‎ 则EF=2a，AF=3﹣a，FG=3﹣a，‎ ‎∴S△EFC+S四边形FCDG=S△EFC+S梯形OFGD﹣S△OCD=a•2a+（3﹣a+4）•（a+1）﹣×1×4=，‎ 解得：a=＜0（舍去）；‎ ‎②若直线在点B的左侧，‎ 令平行于y轴的直线交AB于E，交CA于F，交AD于G，‎ 求得AB的函数为y=﹣x+4，‎ 则EF=FA，‎ 同理求得AD的函数为y=x﹣4，‎ ‎∴AF=FG，‎ 设AF=a＞0，‎ 则EF=a，AF=a，FG=a，∴S△EFC+S△AFG=a•a+a•a=，‎ 解得：a=，∴EG=3．‎ 故线段长为3．‎ ‎21. 如图，在直角坐标系xOy中，二次函数y=x2+（2k﹣1）x+k+1的图象与x轴相交于O、A两点．‎ ‎（1）求这个二次函数的解析式；‎ ‎（2）在这条抛物线的对称轴右边的图象上有一点B，使△AOB的面积等于6，求点B的坐标；‎ ‎（3）对于（2）中的点B，在此抛物线上是否存在点P，使∠POB=90°？若存在，求出点P的坐标，并求出△POB的面积；若不存在，请说明理由．‎ ‎ ‎ 解：①∵函数的图象与x轴相交于O，‎ ‎∴0=k+1，∴k=﹣1，∴y=x2﹣3x，‎ ‎②假设存在点B，过点B做BD⊥x轴于点D，‎ ‎∵△AOB的面积等于6，∴AO•BD=6，‎ 当0=x2﹣3x，‎ x（x﹣3）=0，‎ 解得：x=0或3，∴AO=3，∴BD=4‎ ‎ 即4=x2﹣3x，‎ ‎ 解得：x=4或x=﹣1（舍去）．‎ 又∵顶点坐标为：（ 1.5，﹣2.25）．‎ ‎∵2.25＜4，∴x轴下方不存在B点，‎ ‎∴点B的坐标为：（4，4）；‎ ‎③∵点B的坐标为：（4，4），‎ ‎∴∠BOD=45°，BO==4，‎ 当∠POB=90°，∴∠POD=45°，‎ 设P点横坐标为：﹣x，则纵坐标为：x2﹣3x，‎ 即﹣x=x2﹣3x，‎ 解得x=2 或x=0，‎ ‎∴在抛物线上仅存在一点P （2，﹣2）．∴OP==2，‎ 使∠POB=90°，‎ ‎∴△POB的面积为： PO•BO=×4×2=8．‎ ‎22. 如图，在平面直角坐标系xOy中，顶点为M的抛物线是由抛物线y=x2﹣3向右平移一个单位后得到的，它与y轴负半轴交于点A，点B在该抛物线上，且横坐标为3．‎ ‎（1）求点M、A、B坐标；‎ ‎（2）联结AB、AM、BM，求∠ABM的正切值；‎ ‎（3）点P是顶点为M的抛物线上一点，且位于对称轴的右侧，设PO与x正半轴的夹角为α，当α=∠ABM时，求P点坐标．‎ ‎ ‎ 解：（1）抛物线y=x2﹣3向右平移一个单位后得到的函数解析式为y=（x﹣1）2﹣3，‎ 顶点M（1，﹣3），‎ 令x=0，则y=（0﹣1）2﹣3=﹣2，‎ 点A（0，﹣2），‎ x=3时，y=（3﹣1）2﹣3=4﹣3=1，‎ 点B（3，1）；‎ ‎（2）过点B作BE⊥AO于E，过点M作MF⊥AO于M，‎ ‎∵EB=EA=3，∴∠EAB=∠EBA=45°，‎ 同理可求∠FAM=∠FMA=45°，‎ ‎∴△ABE∽△AMF，∴==，‎ 又∵∠BAM=180°﹣45°×2=90°，∴tan∠ABM==；‎ ‎（3）过点P作PH⊥x轴于H，‎ ‎∵y=（x﹣1）2﹣3=x2﹣2x﹣2，‎ ‎∴设点P（x，x2﹣2x﹣2），‎ ‎①点P在x轴的上方时，=，‎ 整理得，3x2﹣7x﹣6=0，‎ 解得x1=﹣（舍去），x2=3，‎ ‎∴点P的坐标为（3，1）；‎ ‎②点P在x轴下方时，=，‎ 整理得，3x2﹣5x﹣6=0，‎ 解得x1=（舍去），x2=，‎ x=时，x2﹣2x﹣2=﹣×=﹣，‎ ‎∴点P的坐标为（，﹣），‎ 综上所述，点P的坐标为（3，1）或（，﹣）．‎ ‎23.点A在x轴上，OA＝4，将线段OA绕点O顺时针旋转120°至OB的位置．‎ ‎（1）求点B的坐标；‎ ‎（2）求经过A、O、B的抛物线的解析式；‎ ‎（3）在此抛物线的对称轴上，是否存在点P，使得以点P、O、B为顶点的三角形是等腰三角形？若存在，求点P的坐标；若不存在，请说明理由．‎ 解：（1）如图2，过点B作BC⊥y轴，垂足为C．‎ 在Rt△OBC中，∠BOC＝30°，OB＝4，所以BC＝2，．‎ 所以点B的坐标为．‎ ‎（2）因为抛物线与x轴交于O、A(4, 0)，设抛物线的解析式为y＝ax(x－4)，‎ 代入点B，．解得．‎ 所以抛物线的解析式为．‎ ‎（3）抛物线的对称轴是直线x＝2，设点P的坐标为(2, y)．‎ ‎①当OP＝OB＝4时，OP2＝16．所以4+y2＝16．解得．‎ 当P在时，B、O、P三点共线（如图2）．‎ ‎②当BP＝BO＝4时，BP2＝16．所以．解得．‎ ‎③当PB＝PO时，PB2＝PO2．所以．解得．‎ 综合①、②、③，点P的坐标为，如图2所示．‎ 图2 图3‎ ‎24. 已知抛物线y＝－x2＋bx＋c经过A(0, 1)、B(4, 3)两点． ‎ ‎（1）求抛物线的解析式；‎ ‎（2）求tan∠ABO的值；‎ ‎（3）过点B作BC⊥x轴，垂足为C，在对称轴的左侧且平行于y轴的直线交线段AB于点N，交抛物线于点M，若四边形MNCB为平行四边形，求点M的坐标．‎ 图1 ‎ 解：（1）将A(0, 1)、B(4, 3)分别代入y＝－x2＋bx＋c，得 ‎ 解得，c＝1．‎ 所以抛物线的解析式是．‎ ‎（2）在Rt△BOC中，OC＝4，BC＝3，所以OB＝5．‎ 如图2，过点A作AH⊥OB，垂足为H．‎ 在Rt△AOH中，OA＝1，，‎ 所以． ‎ 所以，． ‎ 在Rt△ABH中，．‎ ‎（3）直线AB的解析式为．‎ 设点M的坐标为，点N的坐标为，‎ 那么．‎ 当四边形MNCB是平行四边形时，MN＝BC＝3．‎ 解方程－x2＋4x＝3，得x＝1或x＝3．‎ 因为x＝3在对称轴的右侧（如图4），所以符合题意的点M的坐标为（如图3）．‎ 图3 图4‎