2010长沙中考数学试题及答案 10页

‎2010年长沙市初中毕业学业水平考试试卷 数 学 一、选择题（在下列各题的四个选项中，只有一项是符合题意的。请在答题卡中填涂符合题意的选项。本题共8个小题，每小题3分，共24分）‎ ‎1．4的平方根是 A． B．2 C．±2 D．‎ ‎2．函数的自变量x的取值范围是 A．x＞－1 B．x＜－1 C．x≠-1 D．x≠1‎ ‎3．一个几何体的主视图、左视图、俯视图的图形完全相同，它可能是 A．三棱锥 B．长方体 C．球体 D．三棱柱 ‎4．下列事件是必然事件的是 A．通常加热到100℃，水沸腾；‎ B．抛一枚硬币，正面朝上；‎ C．明天会下雨；‎ D．经过城市中某一有交通信号灯的路口，恰好遇到红灯.‎ ‎．··．‎ ‎5．下列每一组数据中的三个数值分别为三角形的三边长，不能构成直角三角形的是 A．3、4、5 B．6、8、10 C．、2、 D．5、12、13‎ ‎6．已知⊙O1、⊙O2的半径分别是、，若两圆相交，则圆心距O1O2可能取的值是 A．2 B．4 C．6 D．8‎ ‎7．下列计算正确的是 A． B．‎ C． D．‎ O A C B ‎8．如图，在⊙O中，OA＝AB，OC⊥AB，则下列结论错误的是 A．弦AB的长等于圆内接正六边形的边长 ‎ B．弦AC的长等于圆内接正十二边形的边长 ‎ 第8题图 C．‎ D．∠BAC=30°‎ 二、填空题（本题共8个小题，每小题3分，共24分）‎ ‎9．－3的相反数是 ．‎ ‎10．截止到2010年5月31日，上海世博园共接待8 000 000人，用科学记数法表示 是 人．‎ ‎11．如图，O为直线AB上一点，∠COB=26°30′，则∠1= 度．‎ a o b ‎ O A B C ‎1‎ y x B ‎1‎ ‎2‎ ‎3‎ ‎3‎ ‎1‎ ‎2‎ O 第13题图 第12题图 第11题图 ‎12．实数a、b在数轴上位置如图所示，则| a |、| b |的大小关系是 ． ‎ ‎13．已知反比例函数的图象如图，则m的取值范围是 ．‎ ‎14．已知扇形的面积为，半径等于6，则它的圆心角等于 度．‎ ‎15．等腰梯形的上底是4cm，下底是10 cm，一个底角是，则等腰梯形的腰长 是 cm．‎ ‎16．2010年4月14日青海省玉树县发生7.1级大地震后，湘江中学九年级（1）班 的60名同学踊跃捐款．有15人每人捐30元、14人每人捐100元、10人每人 捐70元、21人每人捐50元．在这次每人捐款的数值中，中位数是 .‎ 三、解答题（本题共6个小题，每小题6分，共36分）‎ ‎17．计算：‎ ‎18．先化简，再求值：‎ 其中.‎ ‎ ‎ ‎19．为了缓解长沙市区内一些主要路段交通拥挤的现状，交警队在一些主要路口设立了交通路况显示牌（如图）．已知立杆AB高度是3m，从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°．求路况显示牌BC的高度．‎ 第19题图 ‎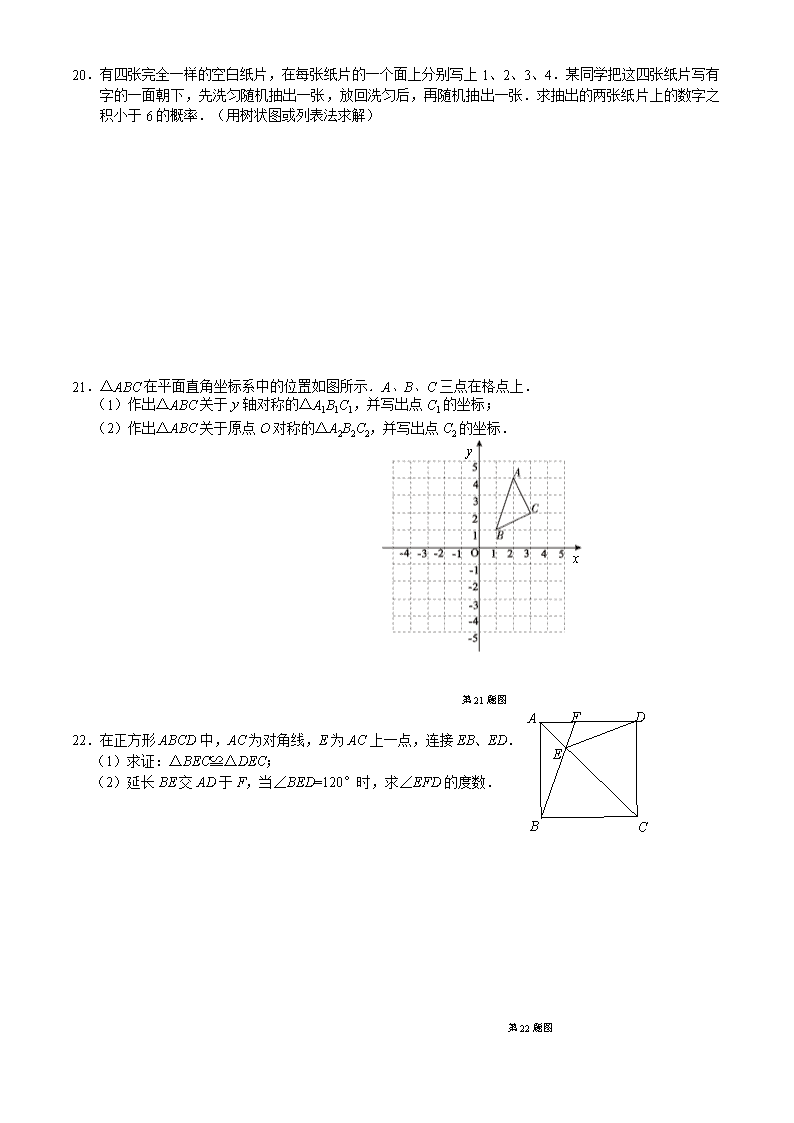20．有四张完全一样的空白纸片，在每张纸片的一个面上分别写上1、2、3、4．某同学把这四张纸片写有字的一面朝下，先洗匀随机抽出一张，放回洗匀后，再随机抽出一张．求抽出的两张纸片上的数字之积小于6的概率．（用树状图或列表法求解）‎ ‎21．△ABC在平面直角坐标系中的位置如图所示．A、B、C三点在格点上．‎ ‎（1）作出△ABC关于轴对称的△A1B1C1，并写出点C1的坐标；‎ y x ‎（2）作出△ABC关于原点O对称的△A2B2C2，并写出点C2的坐标．‎ 第21题图 A F D E B C ‎22．在正方形ABCD中，AC为对角线，E为AC上一点，连接EB、ED．‎ ‎（1）求证：△BEC≌△DEC；‎ ‎（2）延长BE交AD于F，当∠BED=120°时，求∠EFD的度数．‎ 第22题图 四、解答题（本题共2个小题，每小题8分，共16分）‎ ‎23．长沙市某楼盘准备以每平方米5000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望．为了加快资金周转，房地产开发商对价格经过两次下调后，决定以每平方米4050元的均价开盘销售．‎ ‎（1）求平均每次下调的百分率；‎ ‎（2）某人准备以开盘均价购买一套100平方米的房子．开发商还给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，送两年物业管理费．物业管理费是每平方米每月1.5元．请问哪种方案更优惠？‎ ‎24．已知：AB是的弦，D是的中点，过B作AB的垂线交AD的延长线于C．‎ O A D B E C 第24题图 ‎（1）求证：AD＝DC；‎ ‎（2）过D作⊙O的切线交BC于E，若DE＝EC，求sinC．‎ 五、解答题（本题共2个小题，每小题10分，共20分）‎ ‎25．已知：二次函数的图象经过点（1，0），一次函数图象经过原点和点（1，－b），其中且、为实数．‎ ‎（1）求一次函数的表达式（用含b的式子表示）；‎ ‎（2）试说明：这两个函数的图象交于不同的两点；‎ ‎（3）设（2）中的两个交点的横坐标分别为x1、x2，求| x1－x2 |的范围．‎ ‎26．如图，在平面直角坐标系中，矩形OABC的两边分别在x轴和y轴上， cm， OC=8cm，现有两动点P、Q分别从O、C同时出发，P在线段OA上沿OA方向以每秒 cm的速度匀速运动，Q在线段CO上沿CO方向以每秒1 cm的速度匀速运动．设运动时间为t秒．‎ ‎（1）用t的式子表示△OPQ的面积S；‎ ‎（2）求证：四边形OPBQ的面积是一个定值，并求出这个定值；‎ B A P x C Q O y 第26题图 ‎（3）当△OPQ与△PAB和△QPB相似时，抛物线经过B、P两点，过线段BP上一动点M作轴的平行线交抛物线于N，当线段MN的长取最大值时，求直线MN把四边形OPBQ分成两部分的面积之比．‎ ‎2010年长沙市初中毕业学业水平考试试卷 数学参考答案及评分标准 一、选择题（本题共8个小题，每小题3分，共24分）请将你认为正确的选项的代号填在答题卡上．‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 C C C A C B C D 二、填空题（本题共8个小题，每小题3分，共24分）‎ ‎9．3 10．8×106 11．153．5 12．|a|>|b|‎ ‎13．m<1 14．120 15．6 16．50‎ 三、解答题（本题共6个小题，每小题6分，共36分）‎ ‎17．原式＝ …………………………………………………3分 ‎＝ ……………………………………………………………6分 ‎18．原式＝ ……………………………………………2分 ‎＝ ……………………………………………………………4分 当时，原式＝3 …………………………………………………6分 ‎19．解：∵在Rt△ADB中，∠BDA＝45°，AB＝3 ∴DA＝3 …………2分 在Rt△ADC中，∠CDA＝60°∴tan60°=∴CA= …………4分 ‎∴BC=CA－BA=(－3)米 答：路况显示牌BC的高度是(－3)米 ………………………6分 开始 ‎1 2 3 4‎ ‎1 2 3 4 ‎ ‎1 2 3 4 ‎ ‎1 2 3 4 ‎ ‎1 2 3 4 ‎ ‎1 2 3 4 2 4 6 8 3 6 9 12 4 8 12 16或 ‎20．解：（1）‎ 或用列表法 …………3分 ‎ ‎ ‎ ‎（2）P（小于6）＝＝ ………………………………………………………6分 ‎21．解：（1）如图C1（－3，2）…………………3分 ‎（2）如图C2（－3，－2） …………………6分 ‎22．（1）证明：∵四边形ABCD是正方形 ‎∴BC＝CD，∠ECB＝∠ECD＝45°‎ 又EC＝EC …………………………2分 ‎∴△ABE≌△ADE ……………………3分 ‎（2）∵△ABE≌△ADE ‎∴∠BEC＝∠DEC＝∠BED …………4分 ‎ ‎∵∠BED＝120°∴∠BEC＝60°＝∠AEF ……………5分 ‎∴∠EFD＝60°+45°＝105° …………………………6分 四、解答题（本题共2个小题，每小题8分，共16分）‎ ‎23．解：（1）设平均每次降价的百分率是x，依题意得 ………………………1分 ‎5000（1－x）2= 4050 ………………………………………3分 解得：x1=10％ x2＝（不合题意，舍去） …………………………4分 答：平均每次降价的百分率为10％． …………………………………5分 ‎（2）方案①的房款是：4050×100×0.98＝396900（元） ……………………6分 方案②的房款是：4050×100－1.5×100×12×2＝401400（元） ……7分 ‎∵396900＜401400‎ ‎∴选方案①更优惠． ……………………………………………8分 ‎24．证明：连BD∵∴∠A＝∠ABD∴AD＝BD …………………2分 ‎∵∠A+∠C＝90°，∠DBA+∠DBC＝90°∴∠C＝∠DBC∴BD＝DC ‎∴AD＝DC ………………………………………………………4分 ‎（2）连接OD∵DE为⊙O切线 ∴OD⊥DE …………………………5分 ‎ ‎∵，OD过圆心 ∴OD⊥AB 又∵AB⊥BC ∴四边形FBED为矩形∴DE⊥BC ……………………6分 ‎∵BD为Rt△ABC斜边上的中线∴BD＝DC ∴BE＝EC＝DE ‎∴∠C＝45° …………………………………………………7分 ‎∴sin∠C= ………………………………………………………………8分 五、解答题（本题共2个小题，每小题10分，共20分）‎ ‎25．解：（1）∵一次函数过原点∴设一次函数的解析式为y=kx ‎∵一次函数过（1，－b） ∴y=－bx ……………………………3分 ‎（2）∵y=ax2+bx－2过（1，0）即a+b=2 …………………………4分 由得 ……………………………………5分 ‎① ∵△＝‎ ‎∴方程①有两个不相等的实数根∴方程组有两组不同的解 ‎∴两函数有两个不同的交点． ………………………………………6分 ‎（3）∵两交点的横坐标x1、x2分别是方程①的解 ‎∴ ‎ ‎∴＝‎ 或由求根公式得出 ………………………………………………………8分 ‎∵a>b>0，a+b=2 ∴2>a>1‎ 令函数 ∵在1