2012中考数学压轴题及答案40例2 8页

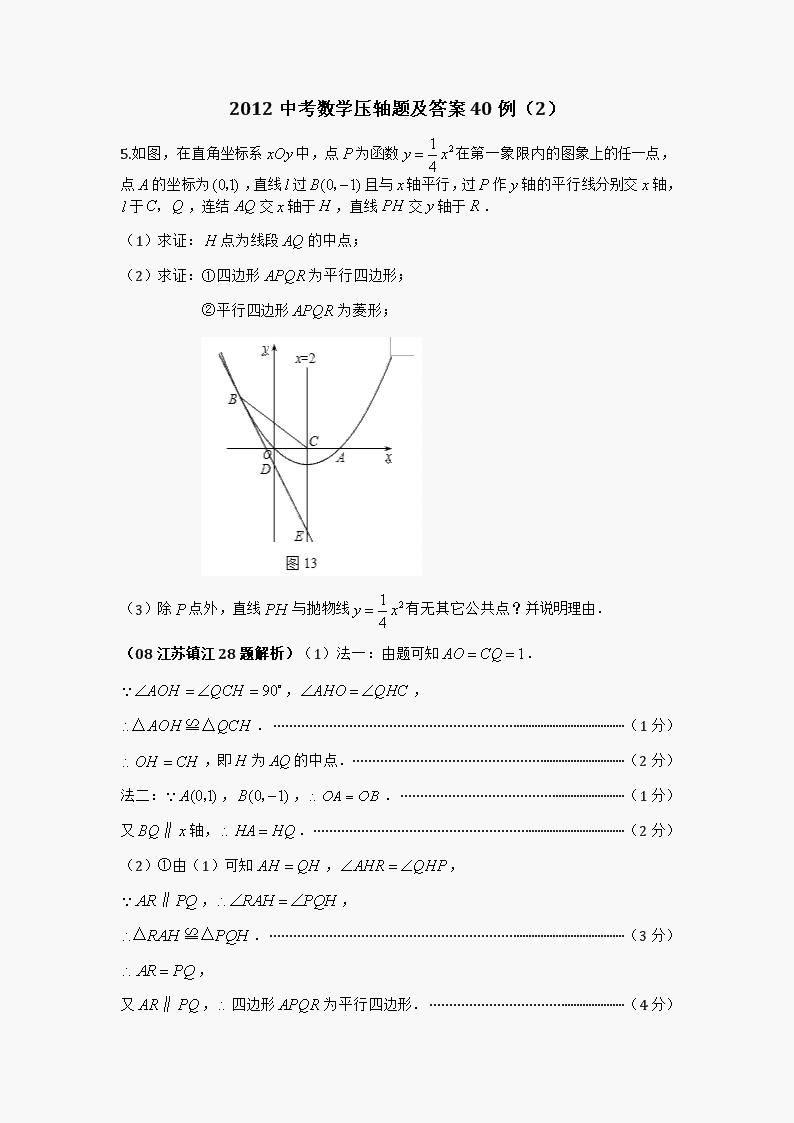
‎2012中考数学压轴题及答案40例（2）‎ ‎5.如图，在直角坐标系中，点为函数在第一象限内的图象上的任一点，点的坐标为，直线过且与轴平行，过作轴的平行线分别交轴，于，连结交轴于，直线交轴于．‎ ‎（1）求证：点为线段的中点；‎ ‎（2）求证：①四边形为平行四边形；‎ ‎②平行四边形为菱形；‎ ‎（3）除点外，直线与抛物线有无其它公共点？并说明理由．‎ ‎（08江苏镇江28题解析）（1）法一：由题可知．‎ ‎，，‎ ‎． （1分）‎ ‎，即为的中点． （2分）‎ 法二：，，． （1分）‎ 又轴，． （2分）‎ ‎（2）①由（1）可知，，‎ ‎，，‎ ‎． （3分）‎ ‎，‎ 又，四边形为平行四边形． （4分）‎ ‎②设，轴，则，则．‎ 过作轴，垂足为，在中，‎ ‎．‎ 平行四边形为菱形． （6分）‎ ‎（3）设直线为，由，得，代入得：‎ ‎ 直线为． （7分）‎ 设直线与抛物线的公共点为，代入直线关系式得：‎ ‎，，解得．得公共点为．‎ 所以直线与抛物线只有一个公共点． （8分）‎ ‎6.如图13，已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2 与x轴交于点C，直线y=-2x-1经过抛物线上一点B(-2,m)，且与y轴、直线x=2分别交于点D、E.‎ ‎（1）求m的值及该抛物线对应的函数关系式；‎ ‎（2）求证：① CB=CE ；② D是BE的中点；‎ ‎（3）若P(x，y)是该抛物线上的一个动点，是否存在这样的点P,使得PB=PE,若存在，试求出所有符合条件的点P的坐标；若不存在，请说明理由.‎ ‎（1）∵ 点B(-2,m)在直线y=-2x-1上，‎ ‎∴ m=-2×(-2)-1=3. ………………………………（2分）‎ ‎∴ B(-2,3)‎ ‎∵ 抛物线经过原点O和点A，对称轴为x=2，‎ ‎∴ 点A的坐标为(4,0) . ‎ 设所求的抛物线对应函数关系式为y=a(x-0)(x-4). ……………………（3分）‎ 将点B(-2,3)代入上式，得3=a(-2-0)(-2-4)，∴ .‎ ‎∴ 所求的抛物线对应的函数关系式为，即. （6分）‎ ‎ （2）①直线y=-2x-1与y轴、直线x=2的交点坐标分别为D(0,-1) E(2,-5).‎ ‎ 过点B作BG∥x轴，与y轴交于F、直线x=2交于G，‎ A B C O D E x y x=2‎ G F H ‎ 则BG⊥直线x=2，BG=4.‎ ‎ 在Rt△BGC中，BC=.‎ ‎∵ CE=5，‎ ‎∴ CB=CE=5. ……………………（9分）‎ ‎②过点E作EH∥x轴，交y轴于H，‎ 则点H的坐标为H(0,-5).‎ 又点F、D的坐标为F(0,3)、D(0,-1)，‎ ‎∴ FD=DH=4，BF=EH=2，∠BFD=∠EHD=90°.‎ ‎ ∴ △DFB≌△DHE （SAS），‎ ‎∴ BD=DE.‎ 即D是BE的中点. ………………………………（11分）‎ ‎ （3） 存在. ………………………………（12分）‎ ‎ 由于PB=PE，∴ 点P在直线CD上，‎ ‎∴ 符合条件的点P是直线CD与该抛物线的交点.‎ ‎ 设直线CD对应的函数关系式为y=kx+b.‎ ‎ 将D(0,-1) C(2,0)代入，得. 解得 .‎ ‎ ∴ 直线CD对应的函数关系式为y=x-1.‎ ‎∵ 动点P的坐标为(x，)，‎ ‎∴ x-1=. ………………………………（13分）‎ 解得 ，. ∴ ，.‎ ‎∴ 符合条件的点P的坐标为(，)或(，).…（14分）‎ ‎(注：用其它方法求解参照以上标准给分.)‎ ‎7.如图，在平面直角坐标系中，抛物线=－++经过A（0，－4）、B（，0）、 C（，0）三点，且-=5．‎ ‎（1）求、的值；（4分）‎ ‎（2）在抛物线上求一点D，使得四边形BDCE是以BC为对 角线的菱形；（3分）‎ ‎（3）在抛物线上是否存在一点P，使得四边形BPOH是以OB为对角线的菱形？若存在，求出点P的坐标，并判断这个菱形是否为正方形？若不存在，请说明理由．（3分）‎ 解： ‎ ‎（解析）解：（1）解法一：‎ ‎∵抛物线=－++经过点A（0，－4），‎ ‎ ∴=－4 ……1分 又由题意可知，、是方程－++=0的两个根，‎ ‎∴+=， =－=6 2分 由已知得（-）=25‎ 又（-）=（+）－4=－24‎ ‎∴ －24=25 ‎ 解得=± 3分 当=时，抛物线与轴的交点在轴的正半轴上，不合题意，舍去．‎ ‎∴=－． 4分 解法二：∵、是方程－++c=0的两个根，‎ ‎ 即方程2－3+12=0的两个根．‎ ‎∴=， 2分 ‎∴－==5，‎ ‎ 解得 =± 3分 ‎ （以下与解法一相同．） ‎ ‎ （2）∵四边形BDCE是以BC为对角线的菱形，根据菱形的性质，点D必在抛物线的对称轴上， 5分 ‎ 又∵=－－－4=－（+）+ 6分 ‎ ∴抛物线的顶点（－，）即为所求的点D． 7分 ‎ （3）∵四边形BPOH是以OB为对角线的菱形，点B的坐标为（－6，0），‎ 根据菱形的性质，点P必是直线=-3与 抛物线=－--4的交点， 8分 ‎ ∴当=－3时，=－×（－3）－×（－3）－4=4， ‎ ‎ ∴在抛物线上存在一点P（－3，4），使得四边形BPOH为菱形． 9分 ‎ 四边形BPOH不能成为正方形，因为如果四边形BPOH为正方形，点P的坐标只能是（－3，3），但这一点不在抛物线上． 10分 ‎8.已知：如图14，抛物线与轴交于点，点，与直线相交于点，点，直线与轴交于点．‎ ‎（1）写出直线的解析式．‎ ‎（2）求的面积．‎ ‎（3）若点在线段上以每秒1个单位长度的速度从向运动（不与重合），同时，点在射线上以每秒2个单位长度的速度从向运动．设运动时间为秒，请写出的面积与的函数关系式，并求出点运动多少时间时，的面积最大，最大面积是多少？‎ ‎（解析）解：（1）在中，令 ‎，‎ ‎， 1分 又点在上 的解析式为 2分 ‎（2）由，得 4分 ‎，‎ ‎， 5分 ‎ 6分 ‎（3）过点作于点 ‎ 7分 ‎ 8分 由直线可得：‎ 在中，，，则 ‎， 9分 ‎ 10分 ‎ 11分 此抛物线开口向下，当时，‎ 当点运动2秒时，的面积达到最大，最大为． 12分