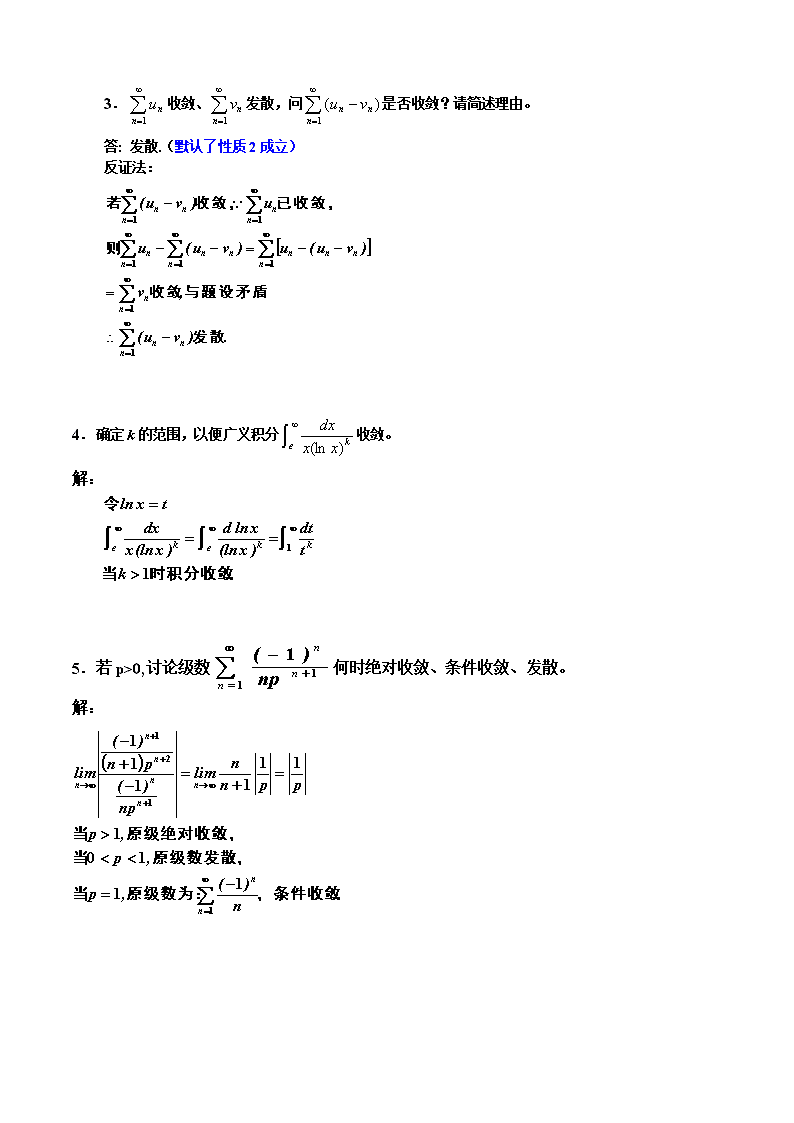- 158.50 KB
- 2021-05-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
专业、班级______________________________学号___________________________姓名_______________________
密 封 线
`````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````````————————————————————————————————————————————————————————————————————
浙江财经学院2008 ~~~2009 学年第 二 学期
《 微积分B下 》课程期中考试卷( A 卷)答卷
年级、专业: 本科08级各专业 考试日期: 09 年 4 月 21 日
题 号
一
二
三
四
五
六
七
八
总 分
得 分
评卷人
(共 五 大题)
一·讨论、简答题(20%)(要求有必要的解题步骤!)
1.设
试通过计算,给出大小关系。
解:
2.设f(x)连续,且。试求f(x)=?
解:(运用了原函数存在性定理,变上限积分)
3.收敛、发散,问是否收敛?请简述理由。
答: 发散.(默认了性质2成立)
反证法:
4.确定k的范围,以便广义积分收敛。
解:
5.若p>0,讨论级数何时绝对收敛、条件收敛、发散。
解:
二.求极限与导数(10%)
1.
解:
原式
2.设,求
解:
三.求积分(30%)
1.
解:
2.
解:
3.
解:
4.
解:
5.
解:
6.
解:
四.应用题(15%)
1.设平面区域由抛物线与直线围成,求:
(1)的面积; (2)绕轴旋转所成旋转体的体积.
解:
图略。
2.某产品的边际利润为(万元/百台)。若在已获最大利润的产量基础上,再生产一百台,总利润将改变多少?
解:
五.级数敛散性判别(25%)
1.
解:
事实上,级数收敛
或者所以原级数绝对收敛,
2.
解:
3.
解:
4.
解:
5.已知正项级数收敛,而数列{vn}有界,试用比较判别法证明数项级数一定是收敛的。
解:因为数列{vn}有界,所以
,,,
,,,,。对正项级数,,则敛散性同;,则敛必敛;,则散必散。若,则绝对收敛;,则发散。