- 395.50 KB
- 2021-05-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2016年安徽省芜湖市繁昌县中考数学二模试卷
一、选择题(每题4分)
1.在﹣4,0,﹣1,3这四个数中,最小的数是( )
A.﹣4 B.2 C.﹣1 D.3
2.计算﹣a2•a3的结果是( )
A.a5 B.﹣a5 C.﹣a6 D.a6
3.如图所示,该几何体的主视图是( )
A. B. C. D.
4.不等式组的解集在数轴上表示正确的是( )
A. B. C. D.
5.与2×的值最接近的正数是( )
A.3 B.4 C.5 D.6
6.如图,这是某地2014年和2015年粮食作物产量的条形统计图,请你根据此图判断下列说法合理的是( )
A.2015年三类农作物的产量比2014年都有增加
B.玉米产量和杂粮产量增长率相当
C.2014年杂粮产量是玉米产量的约七分之一
D.2014年和2015年的小麦产量基本持平
7.某楼盘商品房成交价今年3月份为a元/m3,4月份比3月份减少了8%,若4月份到6月份平均增长率为12%,则6月份商品房成交价是( )
A.a(1﹣8%)(1+12%)元 B.a(1﹣8%)(1+12%)2元
C.(a﹣8%)(a+12%)元 D.a(1﹣8%+12%)元
8.如图,MN与BC在同一条直线上,且MN=BC=2,点B和点N重合,以MN为底作高为2的等腰△PMN,以BC为边作正方形ABCD,若设△PMN沿射线BC方向平移的距离为x,两图形重合部分的面积为y,则y关于x的函数大致图象是( )
A. B. C. D.
9.如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )
A.2:5 B.14:25 C.16:25 D.4:21
10.生产季节性产品的企业,当它的产品无利润时就会及时停产.现有一生产季节性产品的企业,其一年中获得的利润y和月份n之间函数关系式为y=﹣n2+14n﹣24,则该企业一年中应停产的月份是( )
A.1月、2月、3月 B.2月、3月、4月
C.1月、2月、12月 D.1月、11月、12月
二、填空题(每题5分)
11.2016年安徽71所高职院校计划招生9.7万人,其中9.7万人用科学记数法表示为______.
12.分解因式:ab2﹣a=______.
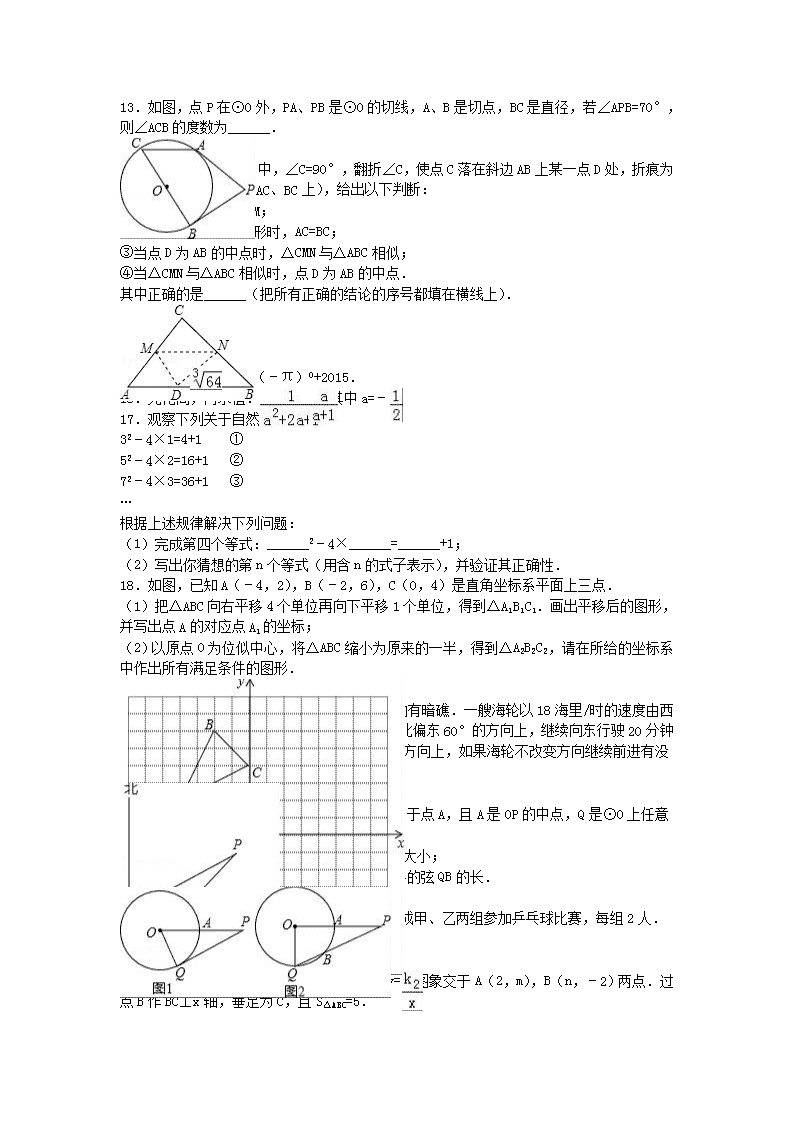
13.如图,点P在⊙O外,PA、PB是⊙O的切线,A、B是切点,BC是直径,若∠APB=70°,则∠ACB的度数为______.
14.如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为MN(点M、N分别在边AC、BC上),给出以下判断:
①当MN∥AB时,CM=AM;
②当四边形CMDN为矩形时,AC=BC;
③当点D为AB的中点时,△CMN与△ABC相似;
④当△CMN与△ABC相似时,点D为AB的中点.
其中正确的是______(把所有正确的结论的序号都填在横线上).
三、解答题
15.计算:﹣|﹣3|﹣(﹣π)0+2015.
16.先化简,再求值:÷(1﹣),其中a=﹣.
17.观察下列关于自然数的等式:
32﹣4×1=4+1 ①
52﹣4×2=16+1 ②
72﹣4×3=36+1 ③
…
根据上述规律解决下列问题:
(1)完成第四个等式:______2﹣4×______=______+1;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
18.如图,已知A(﹣4,2),B(﹣2,6),C(0,4)是直角坐标系平面上三点.
(1)把△ABC向右平移4个单位再向下平移1个单位,得到△A1B1C1.画出平移后的图形,并写出点A的对应点A1的坐标;
(2)以原点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2,请在所给的坐标系中作出所有满足条件的图形.
19.如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘海轮以18海里/时的速度由西向东方向航行,行至A点处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,如果海轮不改变方向继续前进有没有暗礁的危险?
20.已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
(1)如图1,若PQ是⊙O的切线,求∠QOP的大小;
(2)如图2,若∠QOP=90°,求PQ被⊙O截得的弦QB的长.
21.将A,B两男选手和C、D两女选手随机分成甲、乙两组参加乒乓球比赛,每组2人.
(1)求男女混合选手在甲组的概率;
(2)求两个女选手在同一组的概率.
22.如图,一次函数y=k1x+b与反比例函数y=的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=图象上的两点,且y1≥y2,求实数p的取值范围.
23.如图,正方形ABCD边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG=2时,求证:菱形EFGH为正方形;
(3)设AH=x,DG=2x,△FCG的面积为y,试求y的最大值.
2016年安徽省芜湖市繁昌县中考数学二模试卷
参考答案与试题解析
一、选择题(每题4分)
1.在﹣4,0,﹣1,3这四个数中,最小的数是( )
A.﹣4 B.2 C.﹣1 D.3
【考点】有理数大小比较.
【分析】有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.
【解答】解:根据有理数比较大小的方法,可得
﹣4<﹣1<0<3,
在﹣4,0,﹣1,3这四个数中,最小的数是﹣4.
故选:A.
2.计算﹣a2•a3的结果是( )
A.a5 B.﹣a5 C.﹣a6 D.a6
【考点】同底数幂的乘法.
【分析】根据同底数幂的乘法法则求解即可求得答案.
【解答】解:﹣a2•a3=﹣a5
故选:B.
3.如图所示,该几何体的主视图是( )
A. B. C. D.
【考点】简单组合体的三视图.
【分析】找到从几何体的左面看所得到的图形即可.
【解答】解:从几何体的正面看所得到的视图是,
故选:C.
4.不等式组的解集在数轴上表示正确的是( )
A. B. C. D.
【考点】解一元一次不等式组;在数轴上表示不等式的解集.
【分析】先求出每个不等式的解集,再求出不等式组的解集,在数轴上表示不等式组的解集,即可得出选项.
【解答】解:,
∵解不等式①得:x≥1,
解不等式②得:x<2,
∴不等式组的解集为:1≤x<2,
在数轴上表示不等式组的解集为:
,
故选D.
5.与2×的值最接近的正数是( )
A.3 B.4 C.5 D.6
【考点】二次根式的乘除法;估算无理数的大小.
【分析】先利用二次根式的乘法法则得到2×=2,然后进行无理数的估算即可.
【解答】解:2×=2=,
∵16<24<25,
∴4<<5,
∴与2×的值最接近的正数为5.
故选C.
6.如图,这是某地2014年和2015年粮食作物产量的条形统计图,请你根据此图判断下列说法合理的是( )
A.2015年三类农作物的产量比2014年都有增加
B.玉米产量和杂粮产量增长率相当
C.2014年杂粮产量是玉米产量的约七分之一
D.2014年和2015年的小麦产量基本持平
【考点】条形统计图.
【分析】根据条形的高低,来判断小麦、玉米、杂粮在不同年份的增长情况,分别对每一项进行分析,即可得出答案.
【解答】解:A、根据统计图发现小麦有所下降,错误;
B、玉米产量和杂粮产量增加的数量基本一样,但玉米的基数明显>杂粮的基数,所以两者增加的幅度不一样;
C、2014年杂粮产量是玉米产量的约十分之一,错误;
D、根据统计图的高低得出2014年和2015年的小麦产量基本持平,正确.
故选:D.
7.某楼盘商品房成交价今年3月份为a元/m3,4月份比3月份减少了8%,若4月份到6月份平均增长率为12%,则6月份商品房成交价是( )
A.a(1﹣8%)(1+12%)元 B.a(1﹣8%)(1+12%)2元
C.(a﹣8%)(a+12%)元 D.a(1﹣8%+12%)元
【考点】列代数式.
【分析】根据某楼盘商品房成交价今年3月份为a元/m3,4月份比3月份减少了8%,可以求得4月份的成交价,再根据4月份到6月份平均增长率为12%,可以求得6月份商品房成交价,本题得以解决.
【解答】解:由题意可得,
6月份商品房成交价是:a×(1﹣8%)(1+12%)2元,
故选B.
8.如图,MN与BC在同一条直线上,且MN=BC=2,点B和点N重合,以MN为底作高为2的等腰△PMN,以BC为边作正方形ABCD,若设△PMN沿射线BC方向平移的距离为x,两图形重合部分的面积为y,则y关于x的函数大致图象是( )
A. B. C. D.
【考点】动点问题的函数图象.
【分析】分三种情况:①当0≤x<1时,由三角形的面积得出两图形y=x2;②当1≤x≤3时,y=﹣x2+x;③当3<x≤4时,y=(4﹣x)2;即可得出函数的图象.
【解答】解:分三种情况:
①当0≤x<1时,两图形重合部分的面积y=×x×x=x2;
②当1≤x≤3时,两图形重合部分的面积y=×2×﹣×(2﹣x)2=﹣x2+x;
③当3<x≤4时,两图形重合部分的面积y=×(4﹣x)2=(4﹣x)2;
故选:B.
9.如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )
A.2:5 B.14:25 C.16:25 D.4:21
【考点】翻折变换(折叠问题).
【分析】在Rt△BEC中利用勾股定理计算出AB=10,根据折叠的性质得到AD=BD=5,EA=EB,设AE=x,则BE=x,EC=8﹣x,在Rt△BEC中根据勾股定理计算出x=,则EC=8﹣=,
利用三角形面积公式计算出S△BCE=BC•CE=×6×=,在Rt△BED中利用勾股定理计算出ED==,利用三角形面积公式计算出S△BDE=BD•DE=×5×=,然后求出两面积的比.
【解答】解:在Rt△BAC中,BC=6,AC=8,
∴AB==10,
∵把△ABC沿DE使A与B重合,
∴AD=BD,EA=EB,
∴BD=AB=5,
设AE=x,则BE=x,EC=8﹣x,
在Rt△BEC中,∵BE2=EC2+BC2,即x2=(8﹣x)2+62,
∴x=,
∴EC=8﹣x=8﹣=,
∴S△BCE=BC•CE=×6×=,
在Rt△BED中,∵BE2=ED2+BD2,
∴ED==,
∴S△BDE=BD•DE=×5×=,
∴S△BCE:S△BDE=: =14:25.
故选B.
10.生产季节性产品的企业,当它的产品无利润时就会及时停产.现有一生产季节性产品的企业,其一年中获得的利润y和月份n之间函数关系式为y=﹣n2+14n﹣24,则该企业一年中应停产的月份是( )
A.1月、2月、3月 B.2月、3月、4月
C.1月、2月、12月 D.1月、11月、12月
【考点】二次函数的应用.
【分析】根据解析式,求出函数值y等于0时对应的月份,依据开口方向以及增减性,再求出y小于0时的月份即可解答.
【解答】解:∵y=﹣n2+14n﹣24
=﹣(n﹣2)(n﹣12),
当y=0时,n=2或者n=12.
又∵图象开口向下,
∴1月,y<0;2月、12月,y=0.
∴该企业一年中应停产的月份是1月、2月、12月.
故选C.
二、填空题(每题5分)
11.2016年安徽71所高职院校计划招生9.7万人,其中9.7万人用科学记数法表示为 9.7×104 .
【考点】科学记数法—表示较大的数.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:9.7万=97000=9.7×104,
故答案为:9.7×104.
12.分解因式:ab2﹣a= a(b+1)(b﹣1) .
【考点】提公因式法与公式法的综合运用.
【分析】原式提取a,再利用平方差公式分解即可.
【解答】解:原式=a(b2﹣1)=a(b+1)(b﹣1),
故答案为:a(b+1)(b﹣1)
13.如图,点P在⊙O外,PA、PB是⊙O的切线,A、B是切点,BC是直径,若∠APB=70°,则∠ACB的度数为 55° .
【考点】切线的性质;三角形的外角性质;等腰三角形的性质.
【分析】连接OA,根据切线的性质得出∠PAO=∠PBO=90°,求出∠AOB=110°,根据三角形外角性质和等腰三角形性质求出即可.
【解答】解:
连接OA,
∵PA、PB是⊙O的切线,A、B是切点,
∴∠PAO=∠PBO=90°,
∵∠APB=70°,
∴∠AOB=360°﹣90°﹣90°﹣70°=110°,
∴∠ACB+∠OAC=∠AOB=110°,
∵OC=OA,
∴∠ACB=∠OAC,
∴∠ACB=55°
故答案为:55°.
14.如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为MN(点M、N分别在边AC、BC上),给出以下判断:
①当MN∥AB时,CM=AM;
②当四边形CMDN为矩形时,AC=BC;
③当点D为AB的中点时,△CMN与△ABC相似;
④当△CMN与△ABC相似时,点D为AB的中点.
其中正确的是 ①③ (把所有正确的结论的序号都填在横线上).
【考点】相似形综合题.
【分析】①根据平行线的性质得到∠CMN=∠CAB,∠NMD=∠MDA,根据翻折变换的性质得到∠CMN=∠DMN,CM=DM,根据等腰扇形的判定和等量代换证明即可;
②根据矩形的性质得到CE=DE,折叠四边形CEDF是正方形,根据任意一个直角三角形都有一个内接正方形即可得到结论;
③如图2,连接CD,与EF交于点Q,根据直角三角形的性质得到CD=DB=AB,于是得到∠DCB=∠B,由轴对称的性质得到∠CQF=∠DQF=90°,推出∠DCB+∠CFE=90°,由于∠B+∠A=90°,于是得到∠CFE=∠A,即可得到结论;
④由相似三角形的性质得到∠EFD=∠CAB,∠EDF=∠ECF=90°,推出C,E,D,F四点共圆,根据圆周角定理得到∠ACD=∠EFD,等量代换得到∠ACD=∠A,根据等腰三角形的性质得到AD=CD,同理CD=BD,即可得到结论.
【解答】解:①∵MN∥AB,
∴∠CMN=∠CAB,∠NMD=∠MDA,
由翻折变换的性质可知,∠CMN=∠DMN,CM=DM,
∴∠CAB=∠MDA,
∴AM=DM,
∴CM=AM,故①正确;
②根据折叠的性质得到CE=DE,矩形CEDF是正方形,
又任意一个直角三角形都有一个内接正方形满足题意,
故②错误;
③当点D是AB的中点时,△CEF与△ABC相似,
理由如下:如图2,连接CD,与EF交于点Q,
∵CD是Rt△ABC的中线,
∴CD=DB=AB,
∴∠DCB=∠B,
由轴对称的性质可知,∠CQF=∠DQF=90°,
∴∠DCB+∠CFE=90°,
∵∠B+∠A=90°,
∴∠CFE=∠A,
又∵∠C=∠C,
∴△CEF∽△CBA;故③正确;
④∵△CEF与△ABC相似,
∴∠EFD=∠CAB,∠EDF=∠ECF=90°,
∴C,E,D,F四点共圆,
∴∠ACD=∠EFD,
∴∠ACD=∠A,
∴AD=CD,同理CD=BD,
∴点D为AB的中点,
当△ABC∽△EFC时,
点D不是AB的中点,故④错误,
故答案为:①③.
三、解答题
15.计算:﹣|﹣3|﹣(﹣π)0+2015.
【考点】实数的运算.
【分析】原式第一项利用立方根定义计算,第二项利用绝对值的代数意义化简,第三项利用零指数幂法则计算,即可得到结果.
【解答】解:原式=4﹣3﹣1+2015
=2015.
16.先化简,再求值:÷(1﹣),其中a=﹣.
【考点】分式的化简求值.
【分析】先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.
【解答】解:原式=÷
=•(a+1)
=,
当a=﹣时,原式==2.
17.观察下列关于自然数的等式:
32﹣4×1=4+1 ①
52﹣4×2=16+1 ②
72﹣4×3=36+1 ③
…
根据上述规律解决下列问题:
(1)完成第四个等式: 9 2﹣4× 4 = 64 +1;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
【考点】规律型:数字的变化类.
【分析】(1)第一个数是奇数,第二个数是序号数,第三个数是第一个数减1的平方,由此即可写出结果.
(2)第一个数用(2n+1)2表示,接下来不难写出等式,根据恒等式的证明方法进行证明即可.
【解答】解:(1)第四个等式:92﹣4×4=64+1
故答案分别为9,4,64.
(2)(2n+1)2﹣4n=(2n)2+1,
验证:左边=(2n+1)2﹣4×n=4n2+4n+1﹣4n=4n2+1
左边=右边,
所以结论成立.
18.如图,已知A(﹣4,2),B(﹣2,6),C(0,4)是直角坐标系平面上三点.
(1)把△ABC向右平移4个单位再向下平移1个单位,得到△A1B1C1.画出平移后的图形,并写出点A的对应点A1的坐标;
(2)以原点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2,请在所给的坐标系中作出所有满足条件的图形.
【考点】作图-位似变换;作图-平移变换.
【分析】(1)直接利用平移的性质,可分别求得△A1B1C1各点的坐标,继而画出图形;
(2)利用位似的性质,可求得△A2B2C2各点的坐标,继而画出图形.
【解答】解:(1)△A1B1C1如图所示,其中A1的坐标为:(0,1);
(2)符合条件△A2B2C2有两个,如图所示.
19.如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘海轮以18海里/时的速度由西向东方向航行,行至A点处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,如果海轮不改变方向继续前进有没有暗礁的危险?
【考点】解直角三角形的应用-方向角问题.
【分析】过点P作PC⊥AB于C点,在Rt△PBD和Rt△PAC中,根据三角函数AC、BC就可以PC表示出来,在直角△PAC中,根据三角函数,就得到一个关于PC的方程,求得PC.进而判断如果海轮不改变方向继续前进有没有暗礁的危险.
【解答】解:过点P作PC⊥AB于C点,根据题意,得
AB=18×=6(海里),∠PAB=90°﹣60°=30°,∠PBC=90°﹣45°=45°,
∠PCB=90°,
∴PC=BC
在Rt△PAC中
tan30°==
即,
解得PC=(+3)海里,
∵+3>6,
∴海轮不改变方向继续前进无触礁危险.
20.已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
(1)如图1,若PQ是⊙O的切线,求∠QOP的大小;
(2)如图2,若∠QOP=90°,求PQ被⊙O截得的弦QB的长.
【考点】切线的性质.
【分析】(1)先利用切线的性质得到OQ⊥PQ,然后利用锐角三角函数值的定义求∠QOP的大小;
(2)利用垂径定理,作OD⊥BQ于D,如图2,则QD=BD,先利用勾股定理计算出PQ,再证明Rt△QOD∽Rt△QPO,利用相似比计算出QD,从而得到BQ的长.
【解答】解:(1)如图1,∵PQ是⊙O的切线,
∴OQ⊥PQ,
∵A是OP的中点,
∴OP=2OA,
在Rt△OPQ中,cos∠QOP==,
∴∠QOP=60°;
(2)作OD⊥BQ于D,如图2,则QD=BD,
∵∠QOP=90°,OP=4,OQ=2,
∴PQ==2,
∵∠OQD=∠PQO,
∴Rt△QOD∽Rt△QPO,
∴QD:OQ=OQ:QP,即QD:2=2:2,
∴QD=,
∴QB=2QD=.
21.将A,B两男选手和C、D两女选手随机分成甲、乙两组参加乒乓球比赛,每组2人.
(1)求男女混合选手在甲组的概率;
(2)求两个女选手在同一组的概率.
【考点】列表法与树状图法.
【分析】(1)首先根据题意列出表格,然后由树状图求得所有等可能的结果与男女混合选手在甲组的情况,再利用概率公式即可求得答案;
(2)由(1)可求得两个女选手在同一组的情况,再利用概率公式即可求得答案.
【解答】解:(1)所有等可能的结果如下:
甲组
乙组
结果
AB
CD
(AB,CD)
AC
BD
(AC,BD)
AD
BC
(AD,BC)
BC
AD
(BC,AD)
BD
AC
(BD,AC)
CD
AB
(CD,AB)
∵共有6种等可能的结果,男女混合选手在甲组的有4种情况,
∴男女混合选手在甲组的概率为: =;
(2)∵两个女选手在同一组的有2种情况,
∴两个女选手在同一组的概率为: =.
22.如图,一次函数y=k1x+b与反比例函数y=的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=图象上的两点,且y1≥y2,求实数p的取值范围.
【考点】反比例函数与一次函数的交点问题.
【分析】(1)把A、B的坐标代入反比例函数解析式求出m=﹣n,过A作AE⊥x轴于E,过B作BF⊥y轴于F,延长AE、BF交于D,求出梯形BCAD的面积和△BDA的面积,即可得出关于n的方程,求出n的值,得出A、B的坐标,代入反比例函数和一次函数的解析式,即可求出答案;
(2)根据A、B的横坐标,结合图象即可得出答案;
(3)分为两种情况:当点P在第三象限时和当点P在第一象限时,根据坐标和图象即可得出答案.
【解答】解:(1)把A(2,m),B(n,﹣2)代入y=得:k2=2m=﹣2n,
即m=﹣n,
则A(2,﹣n),
过A作AE⊥x轴于E,过B作BF⊥y轴于F,延长AE、BF交于D,
∵A(2,﹣n),B(n,﹣2),
∴BD=2﹣n,AD=﹣n+2,BC=|﹣2|=2,
∵S△ABC=S梯形BCAD﹣S△BDA=5,
∴×(2﹣n+2)×2﹣×(2﹣n)×(﹣n+2),
解得:n=﹣3,
即A(2,3),B(﹣3,﹣2),
把A(2,3)代入y=得:k2=6,
即反比例函数的解析式是y=;
把A(2,3),B(﹣3,﹣2)代入y=k1x+b得:,
解得:k1=1,b=1,
即一次函数的解析式是y=x+1;
(2)∵A(2,3),B(﹣3,﹣2),
∴不等式k1x+b>的解集是﹣3<x<0或x>2;
(3)分为两种情况:当点P在第三象限时,要使y1≥y2,实数p的取值范围是P≤﹣2,
当点P在第一象限时,要使y1≥y2,实数p的取值范围是P>0,
即P的取值范围是p≤﹣2或p>0.
23.如图,正方形ABCD边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG=2时,求证:菱形EFGH为正方形;
(3)设AH=x,DG=2x,△FCG的面积为y,试求y的最大值.
【考点】四边形综合题.
【分析】(1)过F作FM⊥CD,垂足为M,连接GE,由AB与CD平行,利用两直线平行内错角相等得到一对角相等,再由GE为菱形的对角线,利用菱形的性质得到一对内错角相等,利用等式的性质即可得证;
(2)由于四边形ABCD为正方形,四边形HEFG为菱形,那么∠D=∠A=90°,HG=HE,而AH=DG=2,易证△AHE≌△DGH,从而有∠DHG=∠HEA,等量代换可得∠AHE+∠DHG=90°,易证四边形HEFG为正方形;
(3)欲求△FCG的面积,由已知得CG的长易求,只需求出GC边的高,通过证明△AHE≌△MFG可得.
【解答】(1)证明:过F作FM⊥CD,垂足为M,连接GE,
∵CD∥AB,
∴∠AEG=∠MGE,
∵GF∥HE,
∴∠HEG=∠FGE,
∴∠AEH=∠FGM;
(2)证明:在△HDG和△AEH中,
∵四边形ABCD是正方形,
∴∠D=∠A=90°,
∵四边形EFGH是菱形,
∴HG=HE,
在Rt△HDG和△AEH中,
,
∴Rt△HDG≌△AEH(HL),
∴∠DHG=∠AEH,
∴∠DHG+∠AHE=90°
∴∠GHE=90°,
∴菱形EFGH为正方形;
(3)解:过F作FM⊥CD于M,
在△AHE与△MFG中,,
∴△AHE≌△MFG,
∴MF=AH=x,
∵DG=2x,
∴CG=6﹣2x,
∴y=CG•FM=•x•(6﹣2x)=﹣(x﹣)2+,
∵a=﹣1<0,∴当x=时,y最大=.