中考模拟试卷数学卷 11页

‎2011年中考模拟试卷数学卷 考生须知:‎ 1. 本试卷满分120分, 考试时间100分钟.‎ 2. 答题前, 在答题纸上写姓名和准考证号.‎ 3. 必须在答题纸的对应答题位置上答题，写在其他地方无效. 答题方式详见答题纸上的说明.‎ 4. 考试结束后, 试题卷和答题纸一并上交.‎ 试题卷 一、仔细选一选 (本题有10个小题, 每小题3分, 共30分) ‎ ‎ 下面每小题给出的四个选项中, 只有一个是正确的. 注意可以用多种不同的方法来选取正确答案.‎ ‎1．（原创）－5的绝对值是（　　）‎ A．5 B． C． D． ‎ ‎2．（原创）在中，，，，那么的值是（ ）‎ A． B． C． D．‎ ‎3. （原创）用数学的方式理解“两岸猿声啼不住，轻舟已过万重山”和“坐地日行八万里”（只考虑地球的自转），其中蕴含的图形运动是（ ）‎ A．平移和旋转　 B．对称和旋转　　 C．对称和平移　 　D．旋转和平移 ‎4. （改编）如下左图所示的几何体的左视图是（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎5. （原创）为了解我杭州市参加中考的16000名学生的体重情况，抽查了1200名学生的体重进行统计分析．下面四个判断正确的是（ ）‎ A．16000名学生是总体 B．1200名学生的体重是总体的一个样本 C．每名学生是总体的一个个体 D．以上调查是普查 ‎ ‎6．（改编）小明将一张正方形包装纸，剪成图1所示形状，用它包在一个棱长为10的正方体的表面（不考虑接缝），如图2所示．小明所用正方形包装纸的边长至少为（ ）‎ A．40 B． C． D．‎ 第7题图 ‎7．（原创）在□2□8□8的“□”中，任意填上“+”或“－”，可组成若干个不同的二次函数，其中其图象的顶点在x轴上的概率为（ ）‎ A O M N y x 第8题 A． B． C． D．1‎ ‎8.（改编）如图，在平面直角坐标系中，⊙A与y轴相切于原点O，平行于x轴的直线交⊙A于M、N两点，若点M的坐标是(－4，－2)，则点N的坐标为 （ ）‎ A． (1，－2) B．(－1，－2) ‎ ‎ C．(－1.5，－2) D．(1.5，－2)‎ ‎9．（原创）如果一个三角形能够分成两个与原三角形都相似的三角形，我们把这样的三角形称为孪生三角形，那么孪生三角形是（ ）‎ A．不存在 B．等腰三角形 C．直角三角形 D．等腰三角形或直角三角形 ‎（第10题）‎ ‎10．（改编）如图，Rt△ABC中，AC⊥BC，AD平分∠BAC交BC于点D，DE⊥AD交AB于点E，M为AE的中点，BF⊥BC交CM的延长线于点F，BD＝2，CD＝1．下列结论：‎ ‎①∠AED＝∠ADC；②＝；③AC·BE＝2；④ BF＝‎2AC；⑤BE=DE 其中结论正确的个数有 （ ）‎ A．1个 B．2个 C．3个 D．4个 二、认真填一填 (本题有6个小题, 每小题4分, 共24分)‎ ‎ 要注意认真看清题目的条件和要填写的内容, 尽量完整地填写答案。‎ ‎11．（原创）分解因式： ．‎ ‎12．（改编）若一个圆锥的侧面积是18π，侧面展开图是半圆，则该圆锥的底面圆半径是 .‎ ‎13．（原创）关于x的方程的解是非负数，则m的取值范围是 　　．‎ ‎14．（原创）已知、、、、这五个数据，其中、是方程的两个根，这五个数据的平均数是 ，中位数是 .‎ ‎15.（原创）在平面直角坐标系xOy中，直线l的函数解析式为，抛物线的函数解析式为，①　直线至少向上平移 个单位才能与抛物线有交点。②在抛物线上有一个动点A，这个点到直线的最短距离是 。‎ ‎16.(原创) 在平面直角坐标系xOy中，有三条平行的直线，函数解析式依次为，在这三条直线上各有一个动点，依次为A，B，C，，它们的横坐标分别表示为a,b,c。则当a,b,c满足条件 时，这三点不能构成三角形。‎ 三、全面答一答 (本题有8个小题, 共66分) ‎ 解答应写出文字说明, 证明过程或推演步骤. 如果觉得有的题目有点困难, 那么把自己 能写出的解答写出一部分也可以.‎ ‎17．(本小题满分6分) ‎ ‎（原创）先化简，再求代数式的值。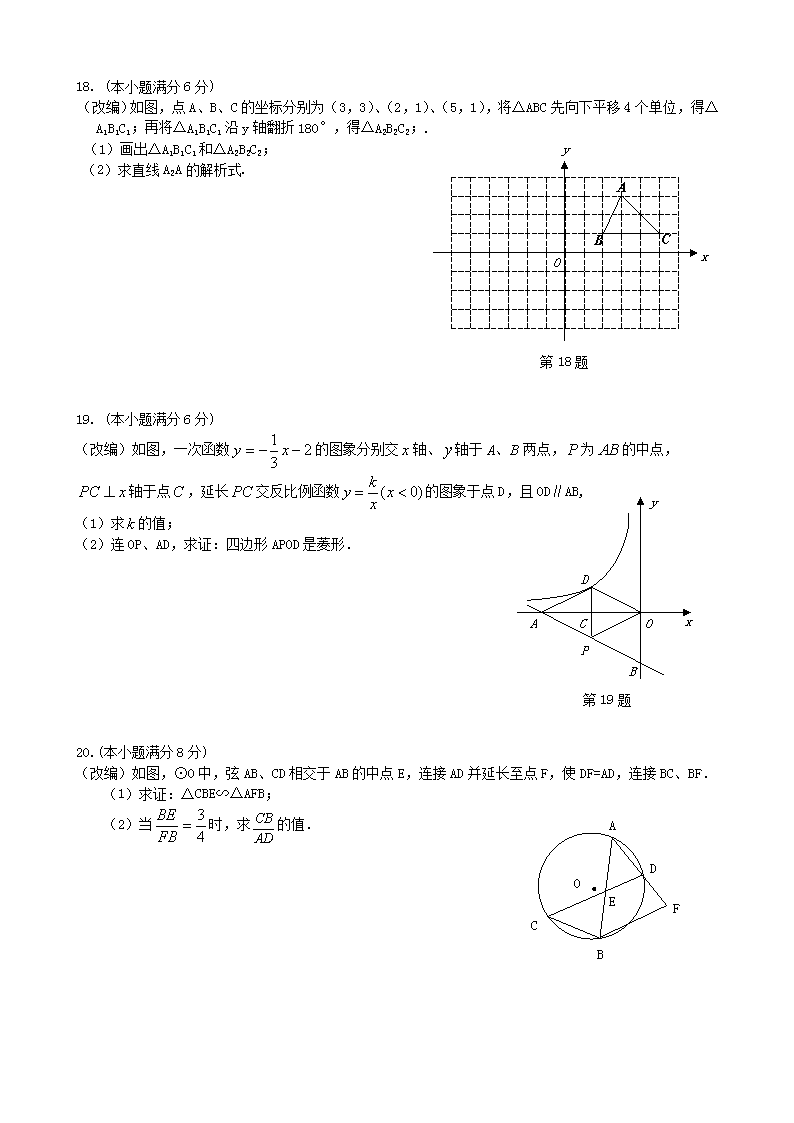‎ ‎，其中 ,请你取一个合适的数作为a的值代入求值.‎ ‎18. (本小题满分6分) ‎ ‎（改编） y x O A B C 如图，点A、B、C的坐标分别为（3，3）、（2，1）、（5，1），将△ABC先向下平移4个单位，得△A1B‎1C1；再将△A1B‎1C1沿y轴翻折180°，得△A2B‎2C2；.‎ ‎（1）画出△A1B‎1C1和△A2B‎2C2；‎ ‎（2）求直线A‎2A的解析式.‎ 第18题 ‎19. (本小题满分6分) ‎ yc ‎（改编）如图，一次函数的图象分别交轴、轴于两点，为的中点，轴于点，延长交反比例函数的图象于点D，且OD∥AB,‎ ‎（1）求的值；‎ ‎（2）连OP、AD，求证：四边形APOD是菱形．‎ Dc xc Oc Cc Ac Pc Bc 第19题 ‎20.(本小题满分8分)‎ ‎（改编）如图，⊙O中，弦AB、CD相交于AB的中点E，连接AD并延长至点F，使DF=AD，连接BC、BF．‎ ‎（1）求证：△CBE∽△AFB；‎ O F D A E B C ‎（2）当时，求的值．‎ ‎21. (本小题满分8分) ‎ ‎（原创）某中学为了充分提高学生积极参与体育活动的积极性举办了“大课间”的活动,让学生自主选择各类活动,校体育组采取抽样调查的方法，从跳绳、呼啦圈、篮球、排球等四个方面调查了若干名学生的兴趣爱好，并将调查的结果绘制成如下的两幅不完整的统计图（如图1，图2要求每位同学只能选择一种自己喜欢的活动；图中用跳绳、呼啦圈、篮球、排球代表喜欢这四种活动中的某一种活动的学生人数），请你根据图中提供的信息解答下列问题：‎ ‎（1）在这次研究中，一共调查了多少名学生？‎ ‎（2）喜欢排球的人数在扇形统计图中所占的圆心角是多少度？‎ ‎（3）补全频数分布折线统计图．‎ 图2‎ 人数 呼啦圈20%‎ 跳绳 排球 篮球 ‎40%‎ ‎50‎ ‎40‎ ‎30‎ ‎20‎ ‎10‎ O 项目 跳绳 呼啦圈 篮球 排球 图1‎ ‎22. (本小题满分8分) ‎ ‎（改编）已知正n边形的周长为60，边长为a 。‎ ‎ ⑴当n=3时，请直接写出a的值；‎ ‎⑵把正n边形的周长与边数同时增加7后，假设得到的仍是正多边形，它的边数为n+7，周长为67，边长为b. 当a = b时，求n 的值。‎ ‎23. (本小题满分10分) ‎ ‎（改编）随着生活水平的提高，人们对环保要求也是越来越高，萧山区内有一家化工厂原来每月利润为120万元．从今年一月起响应政府“实施清洁生产,打造绿色化工”的号召，开始安装使用回收净化设备（安装时间不计），一方面改善了环境，另一方面大大降低原料成本．据测算，使用回收净化设备后的1至月（）的利润的月平均值（万元）满足，第2年的月利润稳定在第1年的第12个月的水平．‎ ‎（1）设使用回收净化设备后的1至月（）的利润和为，写出关于 的函数关系式，并求前几个月的利润和等于840万元？‎ ‎（2）当为何值时，使用回收净化设备后的1至月的利润和与不安装回收净化设备时个月的利润和相等？‎ ‎（3）求使用回收净化设备后两年的利润总和?‎ ‎24. (本小题满分12分) ‎ ‎（原创）如图，直线与直线的图象交于点，与坐标轴分别交于两点，与坐标轴分别交于两点。‎ ‎（1）求点的坐标，并求出经过三点的抛物线函数解析式；‎ ‎（2）题（1）抛物线上的点的横坐标不动，纵坐标扩大一倍后，得到新的抛物线，请写出这个新的抛物线的函数解析式，判断这个抛物线经过平移，轴对称这两种变换后能否经过三点，如果可以，说出变换的过程，如果不可以，请说明理由。‎ ‎（3）在题（1）中的抛物线顶点上方的对称轴上有一动点，在对称轴右侧的抛物线上有一动点，为是否存在这样的动点，使与相似，如存在请求出动点Q的坐标，并直接写出AP的长度。‎ ‎2011年中考模拟试卷数学答题卷 一、仔细选一选 (本题有10个小题, 每小题3分, 共30分) ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 二、认真填一填 (本题有6个小题, 每小题4分, 共24分)‎ ‎11._____________ 12. _____________ 13. _____________ ‎ ‎14. _____________ 15. _____________ 16. _____________ ‎ 三、全面答一答 (本题有8个小题, 共66分) ‎ ‎17．(本小题满分6分) ‎ 先化简，再求代数式的值。‎ ‎，其中 ,请你取一个合适的数作为a的值代入求值.‎ y x O A B C ‎18. (本小题满分6分) ‎ yc ‎19. (本小题满分6分) ‎ Dc Oc Cc Ac xc Pc Bc O F D A E B C ‎20. (本小题满分8分) ‎ ‎21. (本小题满分8分) ‎ ‎（1）‎ ‎（2）‎ ‎（3）‎ 图2‎ 人数 呼啦圈20%‎ 跳绳 排球 篮球 ‎40%‎ ‎50‎ ‎40‎ ‎30‎ ‎20‎ ‎10‎ O 项目 跳绳 呼啦圈 篮球 排球 图1‎ ‎22. (本小题满分10分) ‎ ‎（1）‎ ‎（2）‎ ‎23. (本小题满分10分)‎ 解：（1）‎ ‎（2）‎ ‎（3）‎ ‎24. (本小题满分12分)‎ ‎ ‎ ‎ ‎ ‎2011年中考模拟试卷数学参考答案及评分标准 一、仔细选一选 (本题有10个小题, 每小题3分, 共30分) ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 A A A A B C C B C ‎ D 二、认真填一填 (本题有6个小题, 每小题4分, 共24分)‎ ‎11. 12. 3 13. 且 ‎14. ，4 15. 5， 16. ‎ 三、全面答一答 (本题有8个小题, 共66分) ‎ ‎17．(本小题满分6分) ‎ ‎=‎ ‎=………………………………………………（3分）‎ 在选择适当的值代入正确的得…………（3分）‎ ‎18. (本小题满分6分) ‎ ‎（1）△A1B‎1C1画对得……………………（1分） ‎ ‎ △A2B‎2C2画对得……………………（2分）‎ 设直线的解析式为y=kx+b 把点的坐标A（3，3）的坐标（-3，-1）代入上式得 解得： ………………（2分） 所以直线的解析式为…………………………（1分）‎ ‎19. (本小题满分6分) ‎ ‎（1） ∠AOB=， P为AB中点 ‎ ∴AP=OP ‎ PC⊥AO ‎∴AO=OC=3‎ DO//AB ‎∴∠DOA=∠OAB ‎∴ △AOP≌△OCD ‎∴DC=CP ……………………（2分）‎ 由B点坐标（0，-2），A点坐标（-6，0）‎ 易知tan∠tanOAB=∠AOD=13‎ 所以点D的坐标（-3，1），k=-3 ………………………（2分）‎ ‎(2) 四边形APOD为菱形（对角线互相平分且垂直） …………（2分）‎ ‎20. (本小题满分8分) ‎ ‎（1）证明：∵AE=EB，AD=DF， ∴ED是△ABF的中位线，………………………（1分） ∴ED∥BF， ∴∠CEB=∠ABF，………………………（1分） 又∠C=∠A， ∴△CBE∽△AFB．…………………（2分）‎ ‎（2）解：由（1）知，△CBE∽△AFB， ∴ ……………………………………（2分） 又AF=2AD， ∴……………………（2分）‎ ‎21. (本小题满分8分) ‎ ‎（1）一共调查了100名学生………………………（2分）‎ ‎（2）喜欢排球的人数在扇形统计图中所占的圆心角是36度…………（3分）‎ ‎（3）图形略……………………………（3分）‎ ‎22. (本小题满分10分) ‎ ‎（1）a=20 ……………（2分）‎ ‎（2）a=b，……………（2分）‎ 即（*） ……………（2分） ‎ ‎ ∴ 60n+420=67n,解得n=60 ……………（2分）‎ ‎ 经检验n =60是方程（*）的根。……………（2分）‎ ‎23. (本小题满分10分)‎ 解：（1）y=xw=x(10x+80)=10x2+80x …………（1分）‎ 当10x2+80x=840 …………（1分）‎ 解得x=6，x=-14（舍去）…………（2分，没有舍去扣1分）‎ 答：前6个月的利润和等于700万元 ‎（2）10x2+80x=120x …………（2分）‎ 解得，x=4，x=0（舍去）…………（2分，没有舍去扣1分）‎ 答：当x为4时，使用回收净化设备后的1至x月的利润和与不安装回收净化设备时x个月的利润和相等.‎ ‎（3）12（10×12+80）+12[12（10×12+80）-11（10×11+80）]=6120（万元）……（2分）‎ ‎24. (本小题满分12分)‎ ‎（1）A（4，-1） 抛物线 ……………………………（3分）‎ ‎（2）新的抛物线 ………（1分） ‎ 可以，因为过的抛物线解析式为，顶点为，，可以把抛物线先以轴为对称轴做轴对称变换，然后向左平移各单位，最后向下平移个单位。………（2分）‎ ‎（3）存在，因为A点是抛物线的顶点，所以小于90度，必不可能等于（这个角是钝角）所以要使与相似，只要使等于或者，就可以存在。设抛物线对称轴与轴交点为，直线与轴交点为，则当=时，，所以坐标为（5，0）直线解析式为，与抛物线的交点为（8，3），此时AP=12或………………………（3分）‎ 当=时，∽，所以坐标为（，0）直线解析式为，与抛物线的交点为（12，15），此时AP=24或…………………（3分）‎