中考数学模拟试题及答案一 19页

中考数学模拟试题及答案一 注意事项：‎ ‎1.本试卷共8页，三大题，满分120分，考试时间100分钟.‎ ‎2.请用钢笔功圆珠笔直接答在试卷上.‎ ‎3.答卷前将密封线内的项目填写清楚.‎ 题号 一 二 三 总分 ‎16‎ ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ 得分 评卷人 ‎ ‎ 一、 选择题（每小题3分，共18分）‎ 下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内．‎ ‎1. 的相反数是（ ）‎ A. B. C. D. 5‎ ‎2.2011年3月23日，我省残疾人工作会议在郑州举行.会议提出继续开展全省各级残联扶残助残活动，计划投入8966万元，惠及107万残疾人.8966万用科学记数法表示正确的是（ ）‎ A.9.0×107 B. 9.0×106 C.8.966×107 D.8.966×108‎ ‎3. 一组数据3，4，x，6，7的平均数是5，则这组数据的中位数和方差分别是（ ）‎ A.4和2 B. 5和2 C. 5和4 D. 4和4‎ ‎4. 已知：四边形ABCD的对角线AC、BD相交于点O，给出下列4个条件：①AB∥CD；②OA＝OC；③AB＝CD；④AD∥BC从中任取两个条件，能推出四边形ABCD是平行四边形的概率是（ ）‎ A. B. C. D. ‎ ‎5. 方程的根是（ ）‎ A. x＝3 B. x＝0 C. x1＝3，x2＝0 D. x1＝0，x2＝‎ ‎6. 在平面直角坐标系xoy中，已知A（4，2），B（2，－2），以原点O为位似中心，按位似比1:2把△OAB缩小，则点A的对应点A′的坐标为（ ）‎ A. （3，1） B. （－2，－1）‎ C. （3，1）或（－3，－1） D. （2，1）或（－2，－1）‎ 得分 评卷人 一、 填空题（每小题3分，共27分）‎ ‎7. 分解因式m2 - 2 (m-1) - 1为 .‎ ‎8. 已知：a是的小数部分，则代数式的值为 .‎ ‎9. 一次函数的图像上不重合的两点A（m1，n1），B（m2，n2），且，则函数的图像分布在第 象限.‎ ‎10. 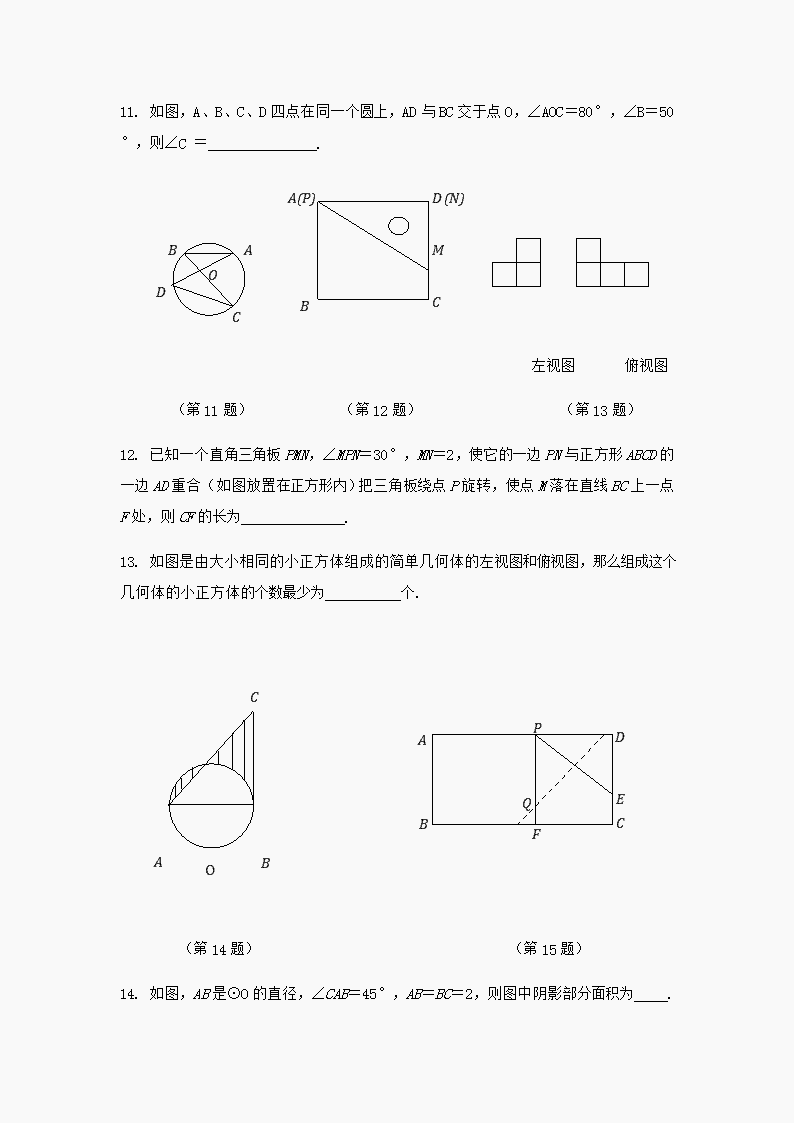已知圆锥的侧面展开图是直径为8cm的半圆，则这个圆锥的侧面积是 cm2.‎ ‎11. 如图，A、B、C、D四点在同一个圆上，AD与BC交于点O，∠AOC＝80°，∠B＝50°，则∠C ＝ .‎ A C B D O M A(P)‎ D B C ‎(N)‎ ‎ ‎ 左视图 俯视图 ‎ （第11题） （第12题） （第13题）‎ ‎12. 已知一个直角三角板PMN，∠MPN＝30°，MN＝2，使它的一边PN与正方形ABCD的一边AD重合（如图放置在正方形内）把三角板绕点P旋转，使点M落在直线BC上一点F处，则CF的长为 .‎ ‎13. 如图是由大小相同的小正方体组成的简单几何体的左视图和俯视图，那么组成这个几何体的小正方体的个数最少为 个.‎ C A D B C E P F Q ‎ ‎ ‎ ‎ A O B ‎ （第14题） （第15题）‎ ‎14. 如图，AB是⊙O的直径，∠CAB＝45°，AB＝BC＝2，则图中阴影部分面积为 .‎ ‎15. 如图，矩形纸片ABCD中，AB＝5cm，BC＝10cm，CD上有一点E，EC＝2cm，AD上有一点P，PA＝6cm，过点P作PF⊥AD交BC于点F，将纸片折叠，使P与E重合，折痕交PF于Q，则线段PQ的长是 cm.‎ 一、 解答题（本大题共8个小题，计75分）‎ 得分 评卷人 ‎16. （8分）已知：A＝，B＝，当x为何值时，A与B的值相等？‎ 评卷人 得分 A B C M N l ‎17. （9分）如图，点C是l上任意一点，CA⊥CB且AC＝BC，过点A作AM⊥l于点M，过点B作BN⊥l于N，则线段MN与AM、BN有什么数量关系，证明你的结论：‎ 得分 评卷人 ‎18. （9分）在“全国亿万学生阳光体育运动”启动后，小华和小敏在课外活动后，报名参加了短跑训练，在近几次百米训练中，所测成绩如图，请根据图中所给信息解答以下问题：‎ 秒 次数 ‎ ‎ （1） 请补齐下面的表格：‎ 秒次 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 小华 ‎13.3‎ ‎13.4‎ ‎13.3‎ ‎13.3‎ 小敏 ‎13.2‎ ‎13.1‎ ‎13.5‎ ‎13.3‎ ‎（2）小华与小敏哪次的成绩最好？最好成绩分别是多少秒？‎ ‎（3）分别计算他们的平均数、极差和方差，如果你是教练请综合比较他们的成绩，分别给予怎样的建议？‎ 得分 评卷人 ‎19.（9分）如图，在梯形ABCD中，AD∥BC, AB = CD,E是AD的中点，AD=4，BC=6,点P是BC边上的动点（不与点B重合），PE与BD相交于点O,设PB的长为x.‎ ‎(1) 当P点在BC边上运动时，求证：△BOP∽△DOE.‎ ‎(2) 当x = （ ）时，四边形ABPE是平行四边形；当x = （ ）时，四边形ABPE是直角梯形；‎ ‎（3）当P在BC上运动的过程中，四边形ABPE会不会是等腰梯形？试说明理由.‎ ‎ ‎ A D B C E O P 得分 评卷人 ‎20.（9分）某公司专销产品A,第一批产品A上市40天恰好全部售完.该公司对第一批产品A上市后的市场销售情况进行了跟踪调查，调查结果如图1和图2所示，其中图1中的折线表示是市场日销售量y（万件）与上市时间t（天）的关系，图2中的折线表示的是每件产品A的日销售利润w（元）与上市时间t（天）的关系.‎ ‎（1）试写出第一批产品A的市场日销售量y（万件）与上市时间t（天）的关系式；‎ w日销售利润（元/件）‎ y日销售量（万件）‎ ‎（2）第一批产品A上市后，哪一天这家公司市场日销售利润最大？最大利润是多少万元？‎ ‎30‎ ‎40‎ t（天）‎ ‎60‎ t（天）‎ ‎20‎ ‎60‎ ‎40‎ 得分 评卷人 ‎21.（10分）如图，双曲线与直线x＝k相交于点P，过点P作PA⊥y轴于A，y轴上的点A1、A2、A3……An的坐标是连续整数，分别过A1、A2……An作x轴的平行线于双曲线（x＞0）及直线x＝k分别交于点B1、B2，……Bn，C1、C2，……Cn.‎ ‎（1）求A的坐标；‎ ‎（2）求及的值；‎ ‎（3）猜想的值（直接写答案）.‎ 得分 评卷人 ‎22.（10分）如图，在梯形ABCD中，AB∥DC，∠ABC＝90°，AB＝2，BC＝4，tan∠ADC＝2.‎ ‎（1）求证：DC＝BC；‎ ‎（2）E是梯形内一点，连接DE、CE，将△DCE绕点C顺时针旋转90°，得△BCF，连接EF.判断EF与CE的数量关系，并证明你的结论；‎ ‎（3）在（2）的条件下，当CE＝2BE，∠BEC＝135°时，求cos∠BFE的值.‎ F A B C D E 得分 评卷人 ‎23. （11分）已知：抛物线（a≠0）的顶点M的坐标为（1,－2）与y轴交于点C（0，），与x轴交于A、B两点（A在B的左边）.‎ ‎（1）求此抛物线的表达式；‎ ‎（2）点P是线段OB上一动点（不与点B重合），点Q在线段BM上移动且∠MPQ＝45°，设线段OP＝x，MQ＝1，求y1与x的函数关系式，并写出自变量x的取值范围；‎ ‎（3）①在（2）的条件下是否存在点P，使△PQB是PB为底的等腰三角形，若存在试求点Q的坐标，若不存在说明理由；‎ ‎②在（1）中抛物线的对称轴上是否存在点F，使△BMF是等腰三角形，若存在直接写出所有满足条件的点F的坐标.‎ Q A B P M x y O C 参考答案:‎ 一、 选择题（每小题3分，共18分）‎ ‎1. B 2.C 3.B 4.C 5.C 6.D 二、 填空题（每题3分，共27分）‎ ‎7. (m- 1)2 8. 1 9. 二、四 10. 8π 11. 30° 12. 或 ‎ ‎13. 5 14.-1 15. ‎ 三、 解答题（本大题共8个小题，计75分）‎ ‎16. 解：由A＝B得： ………………………2分 方程两边同乘以得：‎ 解得：x＝3 ………………………6分 当x＝3时，方程左边＝‎ 右边＝‎ ‎∴左边＝右边 ‎∴当x＝3时，A与B的值相等 ………………………8分 17. 答案：MN＝AM＋BN ………………………1分 证明：∵CA⊥CB ‎ ‎∴∠ACM +∠BCN = 900 ‎ 又∵BN⊥l于N，‎ ‎∴ ∠CBN + ∠BCN = 900‎ ‎∴ ∠ACM=∠CBN ………………………3分 又∵∠AMC =∠BNC=900，AC＝BC，‎ ‎∴ △AMC≌△CNB ………………………6分 ‎∴AM＝CN，BN＝CM， ………………………8分 ‎∴MN＝AM＋BN ………………………9分 ‎18. 解：（1）13.2,13.4 ………………………1分 ‎（2）小华第四次成绩最好是13.2秒；小敏第三次成绩最好是13.1秒；‎ ‎ ………………………2分 ‎（3）（秒） ………………3分 ‎（秒） ………………4分 小华极差为：13.4－13.2＝0.2（秒） ‎ 小敏极差为：13.5－13.1＝0.4（秒） ………………5分 ‎ ‎ ………………8分 他们成绩平均数相同，小敏成绩的极差和方差都比小华大，‎ 因此小华较稳定，小敏有潜力. ………………9分 ‎19．（1） ∵AD∥BC，‎ ‎∴∠CBD = ∠ADB.‎ ‎∵∠BOP=∠DOE，‎ ‎∴△BOP∽△DOE. ………………………………3分 ‎（2）2；3 ………………………………5分 ‎（3）当PB=4时，四边形ABPE是等腰梯形. ………………6分 证明：∵AD∥BC即DE∥PC，‎ ‎ ∴当PC=DE=2,即PB=BC-PC=4时，四边形PCDE是平行四边形，‎ ‎ ∴PE=CD. ‎ 又∵AB=CD， ‎ ‎∴PE=AB.‎ ‎ ∵AE∥PB且AE与PB不相等，‎ ‎∴四边形ABPE是等腰梯形. ………………………………9分 ‎20. 解：（1）①当0＜t≤30时，y＝2t，‎ 当30＜t≤40时，y＝－6t＋240 ………………2分 ‎（2）设该公司的日销售利润为Z万元 ‎①当0＜t≤20时，‎ Z＝y·w＝2t×（3t）＝6t2‎ 当t＝20时，Z最大＝2400（万元） ………………4分 ‎②当20≤t≤30时 Z＝2t×60＝120t 当t＝30时，Z最大＝3600（万元） ………………6分 ‎③当30≤t≤40时 Z＝（－6t＋240）×60＝－360t＋14400‎ ‎∵－360＜0‎ ‎∴当t＝30时，Z最大＝－360×30＋14400＝3600（万元） …………8分 由∵2400＜3600‎ ‎∴当上市第30天时，日销售利润最大，最大利润为3600万元. ………………9分 ‎21. 解：（1）在中当x＝k时，y＝1，‎ ‎∵PA⊥y轴于A，‎ ‎∴A点坐标为（0,1）.………………………………2分 ‎（2）∵A1、A2…An的坐标为连续整数，‎ ‎∴A1为（0，2），A2（0，3）.‎ ‎∴B1为（），C1（k，2），B2（），C2（k，3）.‎ ‎∴A1B1＝，B1C1＝，C2B2＝，A2B2＝，‎ ‎∴，. …………………………6分 ‎（3）提示：An为（0，n＋1）‎ ‎∴Bn为（），Cn（k，n＋1），‎ ‎∴AnBn＝，BnCn＝，‎ ‎∴. …………………………10分 ‎22. （1）证明：作AP⊥DC于点P.‎ ‎∵AB∥CD，∠ABC＝90°，‎ ‎∴四边形APCB是矩形，………………………………1分 ‎∴PC＝AB＝2，AP＝BC＝4.‎ 在Rt△ADP中，tan∠ADC＝ 即＝2，‎ ‎∴DP＝2，‎ ‎∴DC＝DP＋PC＝4＝BC.…………………………3分 ‎（2）EF＝CE.………………………4分 证明如下：‎ 由△DCE绕点C顺时针旋转90°得△BCF，‎ ‎∴CF＝CE，∠ECF＝90°，‎ ‎∴EF＝. …………………………6分 ‎（3）由（2）得∠CEF＝45°.‎ ‎∵∠BEC＝135°，‎ ‎∴∠BEF＝90°. ………………………………7分 设BE＝a，则CE＝2a，由EF＝CE，则EF＝‎ 在Rt△BEF中，由勾股定理得：BF＝3a，‎ ‎∴COS∠BFE＝. ……………………10分 ‎23. 解：（1）∵抛物线的顶点为M（1，﹣2）可设，‎ 由点（0，）得：‎ ‎ ∴.‎ ‎∴即. ……………………3分 ‎（2）在中由y＝0得 解得：， ‎ ‎∴A为（－1，0），B为（3，0） ……………………4分 ‎∵M（1，－2）‎ ‎∴∠MBO＝45°，MB＝‎ ‎∴∠MPQ＝45°‎ ‎∠MBO＝∠MPQ 又∵∠M＝∠M ‎∴△MPQ∽△MPB ……………………5分 ‎∴‎ ‎∴‎ 即 ‎∴（0≤x＜3）. ‎ ‎…………………………7分（自变量取值范围1分）‎ ‎（3）①存在点Q，使QP＝QB，即△PQB是以PB为底的等腰三角形，作PB的垂直平分线交BM于Q，则QP＝QB.‎ ‎∴∠QPB＝∠MBP＝45°‎ 又∵∠MPQ＝45°，‎ ‎∴此时MP⊥x轴 ‎∴P为（1，0）， ‎ ‎∴PB＝2.‎ ‎∴Q的坐标为（2，1）. …………………………9分 ‎②F1（1，0），F2（1，），F3（1，），F4（1，2）.‎ ‎………………………………11分 高考资源网