中考数学规律题专题讲解 6页

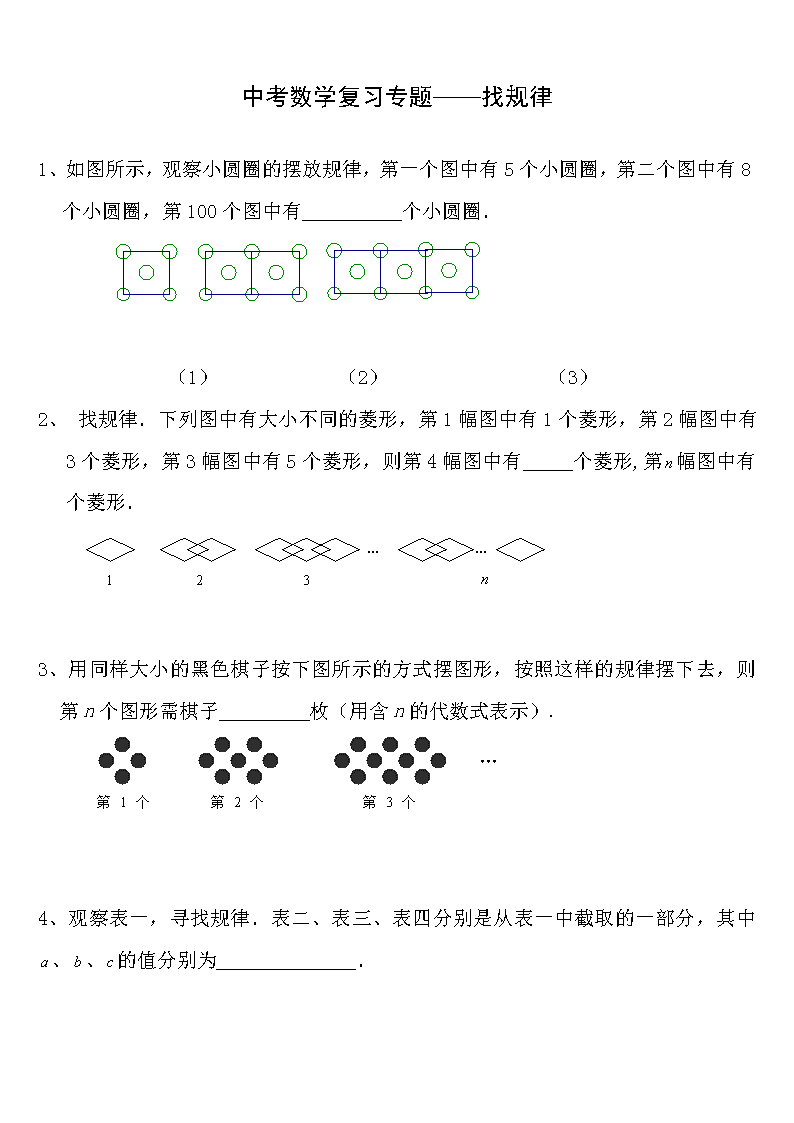
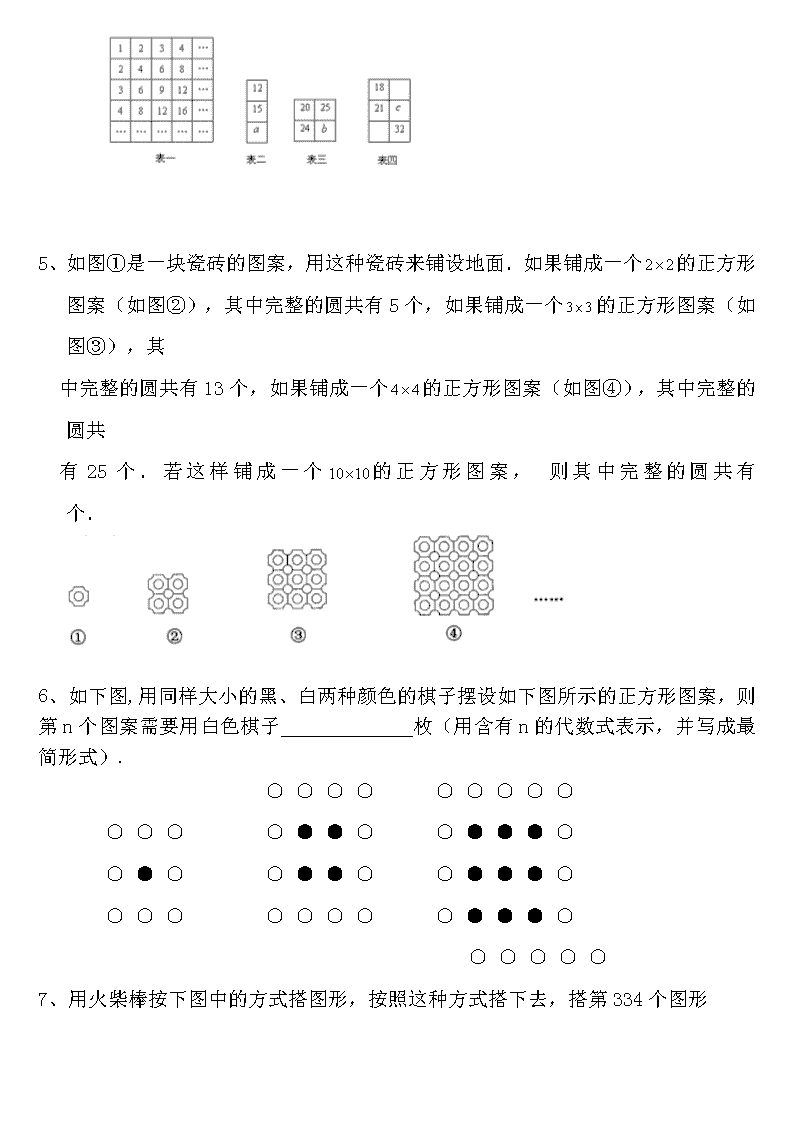
中考数学复习专题——找规律 ‎1、如图所示，观察小圆圈的摆放规律，第一个图中有5个小圆圈，第二个图中有8个小圆圈，第100个图中有__________个小圆圈．‎ ‎ （1） （2） （3）‎ ‎2、 找规律．下列图中有大小不同的菱形，第1幅图中有1个菱形，第2幅图中有3个菱形，第3幅图中有5个菱形，则第4幅图中有 个菱形,第幅图中有 个菱形．‎ ‎1‎ ‎2‎ ‎3‎ ‎…‎ ‎…‎ ‎3、用同样大小的黑色棋子按下图所示的方式摆图形，按照这样的规律摆下去，则第n个图形需棋子 枚（用含n的代数式表示）.‎ 第1个图 第2个图 第3个图 ‎…‎ ‎4、观察表一，寻找规律．表二、表三、表四分别是从表一中截取的一部分，其中、、的值分别为______________．‎ ‎ ‎ ‎5、如图①是一块瓷砖的图案，用这种瓷砖来铺设地面．如果铺成一个的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个的正方形图案（如图③），其 中完整的圆共有13个，如果铺成一个的正方形图案（如图④），其中完整的圆共 有25个．若这样铺成一个的正方形图案， 则其中完整的圆共有 个．‎ ‎ ‎ ‎6、 如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案，则第n个图案需要用白色棋子 枚（用含有n的代数式表示，并写成最简形式）.‎ ‎ ○ ○ ○ ○ ○ ○ ○ ○ ○‎ ‎○ ○ ○ ○ ● ● ○ ○ ● ● ● ○‎ ‎○ ● ○ ○ ● ● ○ ○ ● ● ● ○‎ ‎○ ○ ○ ○ ○ ○ ○ ○ ● ● ● ○‎ ‎ ○ ○ ○ ○ ○‎ ‎7、用火柴棒按下图中的方式搭图形，按照这种方式搭下去，搭第334个图形 ‎ 需 根火柴棒。‎ ‎ ‎ ‎8、将正整数按如图5所示的规律排列下去，若有序实数对（，）表示第排，从左到右第个数，如（，）表示实数，则表示实数的有序实数对是 ．‎ 第一排 第二排 第三排 第四排 ‎6‎ ‎┅┅‎ ‎10‎ ‎9‎ ‎8‎ ‎7‎ ‎3‎ ‎2‎ ‎1‎ ‎5‎ ‎4‎ ‎9、如图 ２ ，用n表示等边三角形边上的小圆圈，f(n)表示这个三角形中小圆圈的总数，那么f(n)和n的关系是 　　　　‎ ‎10、观察图4的三角形数阵，则第50行的最后一个数是 （ ）‎ ‎ 1‎ ‎ -2 3‎ ‎ -4 5 -6‎ ‎ 7 -8 9 -10‎ ‎ 。。。。。。‎ ‎11、 下列图案由边长相等的黑、白两色正方形按一定规律拼接而成，依此规律，第n个图案中白色正方形的个数为___________．‎ 第一个 第二个 第三个 ‎……‎ 第n个 ‎12、 观察下列各式：‎ ‎ ……‎ 猜想： ．‎ ‎（2013）16. 如下图，每一幅图中均含有若干个正方形，第1幅图中有1个正方形；第2幅图中有5个正方形；…………按这样的规律下去，第6幅图中有___________个正方形。‎ ‎ ‎ ‎（2011）15、如图6，这是边长为1的等边三角形摆出的一系列图形，按这种方式摆下去，第n个图形的周长为 .‎ ‎（2008）15．观察表一，寻找规律．表二、表三分别是从表一中选取的一部分，则a+b的值为 ‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎…‎ ‎1‎ ‎3‎ ‎5‎ ‎7‎ ‎…‎ ‎2‎ ‎5‎ ‎8‎ ‎11‎ ‎…‎ ‎3‎ ‎7‎ ‎11‎ ‎15‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎11‎ ‎14‎ a ‎11‎ ‎13‎ ‎17 ‎ b 表一 表二 表三 答案解析：‎ ‎1解析：n=1时，m=5．n再每增加一个数时，m就增加3个数．解答：根据所给的具体数据，发现：8=5+3，11=5+3×2，14=5+3×3，…．以此类推，第n个圈中，m=5+3（n-1）=3n+2．‎ ‎2解析：分析可得：第1幅图中有1×2-1=1个，第2幅图中有2×2-1=3个，第3幅图中有3×2-1=5个，…，故第n幅图中共有2n-1个 ‎3解析：在4的基础上，依次多3个，得到第n个图中共有的棋子数．‎ 观察图形，发现：在4的基础上，依次多3个．即第n个图中有4+3（n-1）=3n+1．当n=6时，即原式=19．故第6个图形需棋子19枚 ‎4解析：此题只要找出截取表一的那部分，并找出其规律即可解．‎ 解答：解：表二截取的是其中的一列：上下两个数字的差相等，所以a=15+3=18． 表三截取的是两行两列的相邻的四个数字：右边一列数字的差应比左边一列数字的差大1，所b=24+25-20+1=30． 表四中截取的是两行三列中的6个数字：18是3的6倍，则c应是4的7倍，即28． 故选D．‎ 认真观察表格，熟知各个数字之间的关系：第一列是1，2，3，…；第二列是对应第一列的2倍；等三列是对应第一列的3倍 ‎5解析：据给出的四个图形的规律可以知道，组成大正方形的每个小正方形上有一个完整的圆，因此圆的数目是大正方形边长的平方，每四个小正方形组成一个完整的圆，从而可得这样的圆是大正方形边长减1的平方，从而可得若这样铺成一个10×10的正方形图案，则其中完整的圆共有102+（10-1）2=181个．‎ 解答：解：分析可得完整的圆是大正方形的边长减1的平方，从而可知铺成一个10×10的正方形图案中，完整的圆共有102+（10-1）2=181个．‎ 点评：本题难度中等，考查探究图形的规律．本题也只可以直接根据给出的四个图形中计数出的圆的个数，找出数字之间的规律得出答案．‎ ‎6解析：解：第1个正方形图案有棋子共32=9枚，其中黑色棋子有12=1枚，白色棋子有（32-12）枚； 第2个正方形图案有棋子共42=16枚，其中黑色棋子有22=4枚，白色棋子有（42-22）枚； …由此可推出想第n个图案的白色棋子数为（n+2）2-n2=4（n+1）． 故第n个图案的白色棋子数为（n+2）2-n2=4（n+1）．‎ 点评：根据图形提供的信息探索规律，是近几年较流行的一种探索规律型问题．解决这类问题首先要从简单图形入手，抓住随着“编号”或“序号”增加时，后一个图形与前一个图形相比，在数量上增加（或倍数）情况的变化，找出数量上的变化规律，从而推出一般性的结论 ‎7解析：根据题意分析可得： 搭第1个图形需12根火柴； 搭第2个图形需12+6×1=18根； 搭第3个图形需12+6×2=24根； … 搭第n个图形需12+6（n-1）=6n+6根．‎ 解答：解：搭第334个图形需6×334+6=2010根火柴棒 ‎8解析：寻找规律，然后解答．每排的数字个数就是排数；且奇数排从左到右，从小到大，而偶数排从左到右，从大到小．‎ 解答：解：观察图表可知：每排的数字个数就是排数；且奇数排从左到右，从小到大，而偶数排从左到右，从大到小．实数15=1+2+3+4+5，则17在第6排，第5个位置，即其坐标为（6，5）．故答案填：（6，5）．‎ 对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．‎ ‎9解析：根据题意分析可得：第n行有n个小圆圈．故f（n）和n的关系是ƒ（n）= （n2+n）．‎ ‎10解析：根据题意可得：第n行有n个数；且第n行第一个数的绝对值为 +1，最后一个数的绝对值为 +n；奇数为正，偶数为负；故第50行的最后一个数是1275．‎ 解答：解：第n行第一个数的绝对值为 +1，最后一个数的绝对值为 +n，‎ 奇数为正，偶数为负， 第50行的最后一个数是1275‎ 第一个图中白色正方形的个数为3×3-1； 第二个图中白色正方形的个数为3×5-2 第三个图中白色正方形的个数为3×7-3； … 当其为第n个时，白色正方形的个数为3（2n+1）-n=5n+3‎ ‎12解析：根据所给的等式，可以发现右边的底数是前边的底数的和，指数是平方，则最后的底数是1+2+3+..+10=5×11=55，则原式=552．解答：解：根据分析最后的底数是1+2+3+..+10=5×11=55，则原式=552．‎ 故答案552‎