上海市浦东新区中考二模数学试卷答案 9页

浦东新区2015年中考二模 ‎ 数学试卷 （2015.4.21）‎ 考生注意：‎ ‎1．本试卷含三个大题，共25题；‎ ‎2．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；‎ ‎3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】‎ ‎1．下列等式成立的是 ( )‎ ‎（A）； （B）； （C）； （D）．‎ ‎2．下列各整式中，次数为5次的单项式是( )‎ ‎（A）xy4； （B）xy5； （C）x+y4； （D）x+y5．‎ ‎3．如果最简二次根式与是同类二次根式，那么x的值是( )‎ ‎ （A）-1； （B）0； （C）1； （D）2．‎ ‎4．如果正多边形的一个内角等于135度，那么这个正多边形的边数是( )‎ ‎ （A）5； （B）6； （C）7； （D）8．‎ ‎5．下列说法中，正确的个数有( )‎ ‎ ①一组数据的平均数一定是该组数据中的某个数据；‎ ‎ ②一组数据的中位数一定是该组数据中的某个数据；‎ ‎ ③一组数据的众数一定是该组数据中的某个数据．‎ ‎（A）0个； （B）1个； （C）2个； （D）3个．‎ 6． 已知四边形ABCD是平行四边形，对角线AC与BD相交于点O，那么下列结论中正确 ‎ 的是( )‎ ‎（A）当AB=BC时，四边形ABCD是矩形；‎ ‎（B）当AC⊥BD时，四边形ABCD是矩形；‎ ‎（C）当OA=OB时，四边形ABCD是矩形；‎ ‎（D）当∠ABD=∠CBD时，四边形ABCD是矩形．‎ 二、填空题：（本大题共12题，每题4分，满分48分）‎ ‎【请将结果直接填入答题纸的相应位置上】‎ ‎7．计算：= ．‎ ‎8．分解因式：= ．‎ ‎9．方程的解是 ．‎ ‎10．已知分式方程，如果设，那么原方程可化为关于y的整式方程是 ．‎ ‎11．如果反比例函数的图像经过点（3,-4），那么这个反比例函数的比例系数是 ．‎ ‎12．如果随意把各面分别写有数字“1”、“2”、“3”、“4”、“5”、“6”的骰子抛到桌面上，那 ‎ 么正面朝上的数字是合数的概率是 ．‎ 13． 为了解某山区金丝猴的数量，科研人员在该山区不同的地方捕获了15只金丝猴，并在 它们的身上做上标记后放回该山区．过段时间后，在该山区不同的地方又捕获了32只 金丝猴，其中4只身上有上次做的标记，由此可以估计该山区金丝猴的数量约有 只．‎ ‎14．已知点G是△ABC的重心，，，那么向量用向量、表示为 ．‎ ‎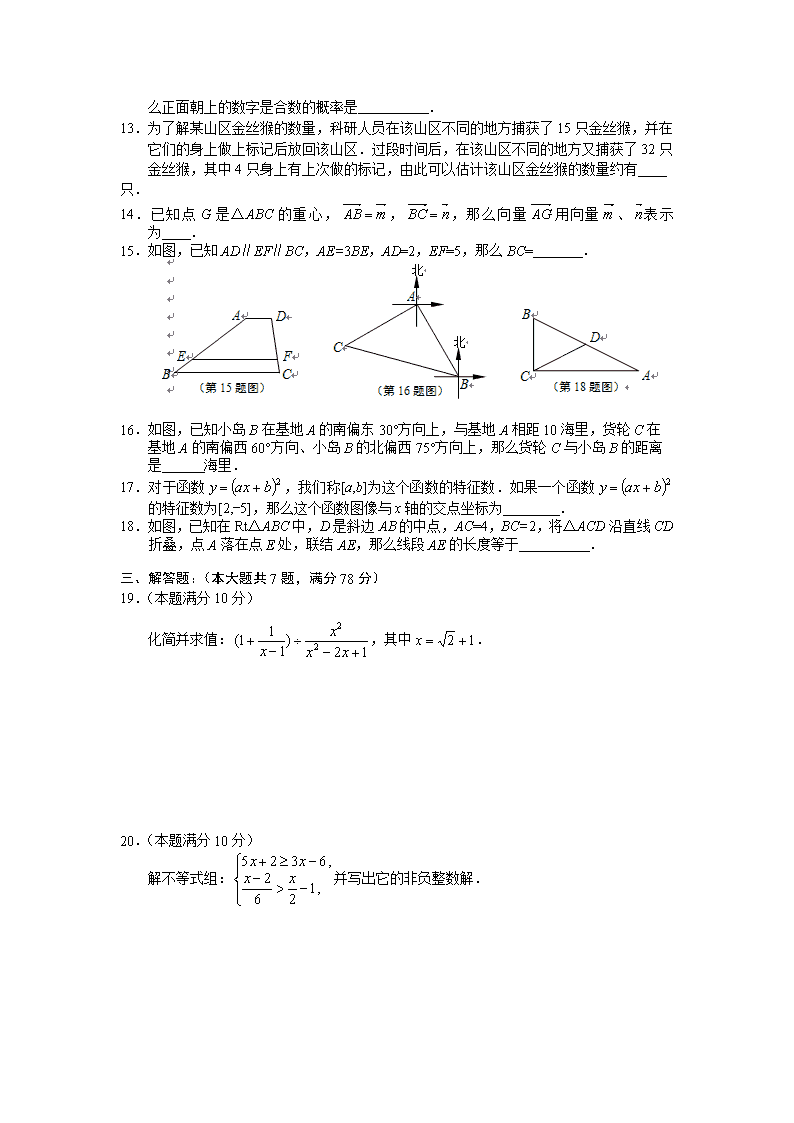15．如图，已知AD∥EF∥BC，AE=3BE，AD=2，EF=5，那么BC= ．‎ ‎16．如图，已知小岛B在基地A的南偏东30°方向上，与基地A相距10海里，货轮C在 基地A的南偏西60°方向、小岛B的北偏西75°方向上，那么货轮C与小岛B的距离 是 海里．‎ ‎17．对于函数，我们称[a,b]为这个函数的特征数．如果一个函数的特征数为[2,-5]，那么这个函数图像与x轴的交点坐标为 ．‎ ‎18．如图，已知在Rt△ABC中，D是斜边AB的中点，AC=4，BC=2，将△ACD沿直线CD折叠，点A落在点E处，联结AE，那么线段AE的长度等于 ．‎ 三、解答题：（本大题共7题，满分78分）‎ ‎19．（本题满分10分）‎ 化简并求值：，其中．‎ ‎20．（本题满分10分）‎ 解不等式组：并写出它的非负整数解．‎ A B C D E ‎（第21题图）‎ F ‎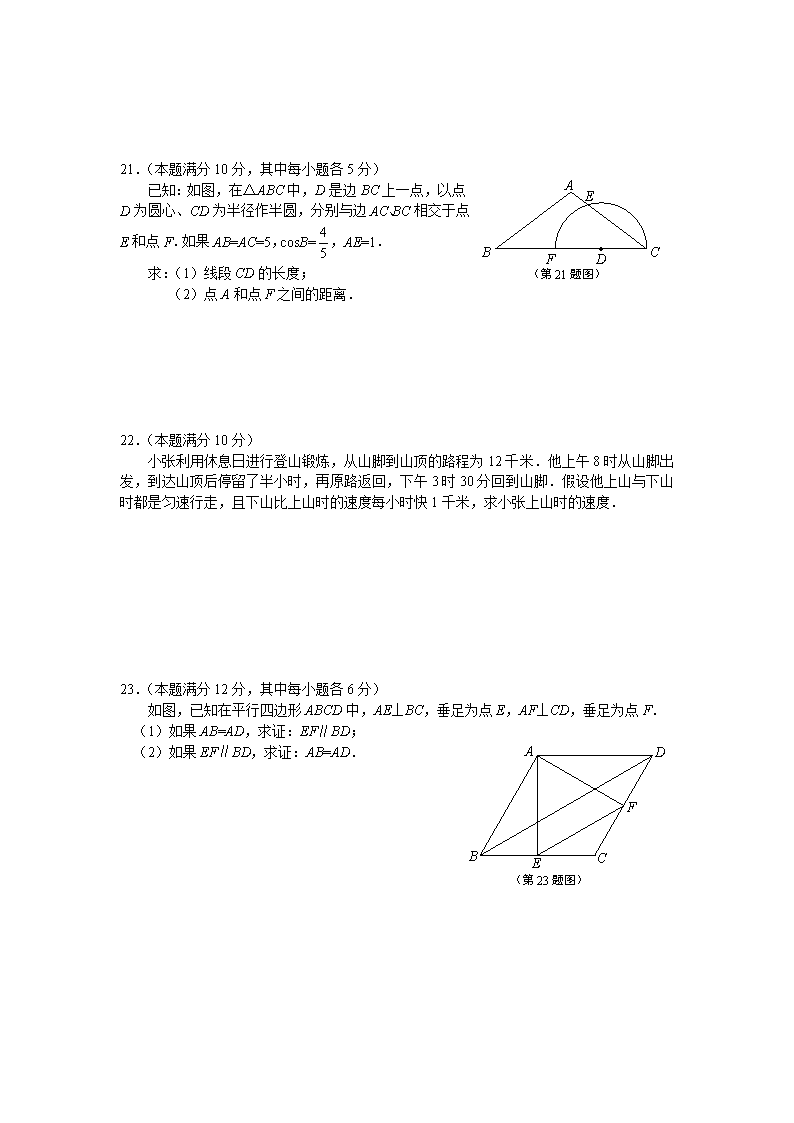21．（本题满分10分，其中每小题各5分）‎ 已知：如图，在△ABC中，D是边BC上一点，以点D为圆心、CD为半径作半圆，分别与边AC、BC相交于点E和点F．如果AB=AC=5，cosB=，AE=1．‎ 求：（1）线段CD的长度；‎ ‎（2）点A和点F之间的距离．‎ ‎22．（本题满分10分）‎ 小张利用休息日进行登山锻炼，从山脚到山顶的路程为12千米．他上午8时从山脚出发，到达山顶后停留了半小时，再原路返回，下午3时30分回到山脚．假设他上山与下山时都是匀速行走，且下山比上山时的速度每小时快1千米，求小张上山时的速度．‎ ‎23．（本题满分12分，其中每小题各6分）‎ 如图，已知在平行四边形ABCD中，AE⊥BC，垂足为点E，AF⊥CD，垂足为点F．‎ A B C D E F ‎（第23题图）‎ ‎（1）如果AB=AD，求证：EF∥BD；‎ ‎（2）如果EF∥BD，求证：AB=AD．‎ ‎24．（本题满分12分，其中第（1）小题3分，第（2）小题4分，第（3）小题5分）‎ B A C O x y ‎（第24题图）‎ 已知：如图，直线y=kx+2与x轴的正半轴相交于点A（t,0）、与y轴相交于点B，抛物线经过点A和点B，点C在第三象限内，且AC⊥AB，tan∠ACB=．‎ ‎（1）当t=1时，求抛物线的表达式；‎ ‎（2）试用含t的代数式表示点C的坐标；‎ ‎（3）如果点C在这条抛物线的对称轴上，求t的值．‎ ‎25．（本题满分14分，其中第（1）小题3分，第（2）小题6分，第（3）小题5分）‎ 如图，已知在△ABC中，射线AM∥BC，P是边BC上一动点，∠APD=∠B，PD交射线AM于点D，联结CD．AB=4，BC=6，∠B=60°．‎ ‎（1）求证：；‎ ‎（2）如果以AD为半径的圆A与以BP为半径的圆B相切，求线段BP的长度；‎ ‎（3）将△ACD绕点A旋转，如果点D恰好与点B重合，点C落在点E的位置上，求此时∠BEP的余切值．‎