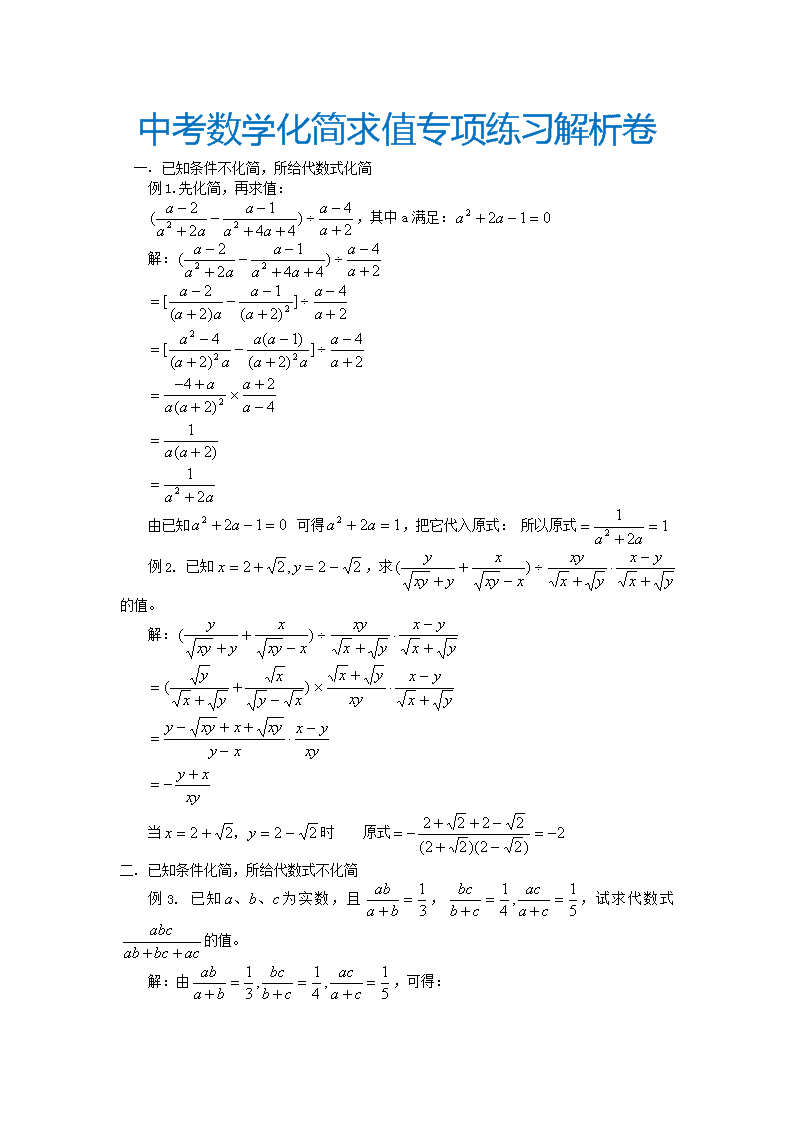中考数学化简求值专项练习试题较高难 4页

中考数学化简求值专项练习（较高难度）‎ ‎ 一. 已知条件不化简，所给代数式化简 ‎ 例1.先化简，再求值：‎ ‎ ，其中a满足：‎ ‎ 例2. 已知，求的值。‎ 例3. 已知条件化简，所给代数式不化简 ‎ 例3. 已知为实数，且，，试求代数式的值。‎ 例4. 已知条件和所给代数式都要化简 ‎ 例4.若，则的值是（ ）‎ ‎ A. B. C. D. ‎ ‎ 例5. 已知，且满足，求的值。‎ 中考数学化简求值专项练习解析卷 ‎ 一. 已知条件不化简，所给代数式化简 ‎ 例1.先化简，再求值：‎ ‎ ，其中a满足：‎ ‎ 解：‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 由已知 可得，把它代入原式： 所以原式 ‎ 例2. 已知，求的值。‎ ‎ 解：‎ ‎ ‎ ‎ ‎ ‎ 当时 原式 二. 已知条件化简，所给代数式不化简 ‎ 例3. 已知为实数，且，，试求代数式的值。‎ ‎ 解：由，可得：‎ ‎ ‎ ‎ 所以 所以 所以 三. 已知条件和所给代数式都要化简 ‎ 例4.若，则的值是（ ）‎ ‎ A. B. C. D. ‎ ‎ 解：因为 所以 所以 ‎ 所以 所以 ‎ 例5. 已知，且满足，求的值。‎ ‎ 解：因为 ‎ 所以 ‎ 所以 ‎ 所以或 ‎ 由 ‎ 故有 ‎ 所以 ‎ ‎ ‎ ‎ ‎ ‎ ‎ 评注：本题应先对已知条件进行变换和因式分解，并由确定出，然后对所给代数式利用立方和公式化简，从而问题迎刃而解。‎ ‎ ‎