中考数学压轴题破解策略专题19中点模型 9页

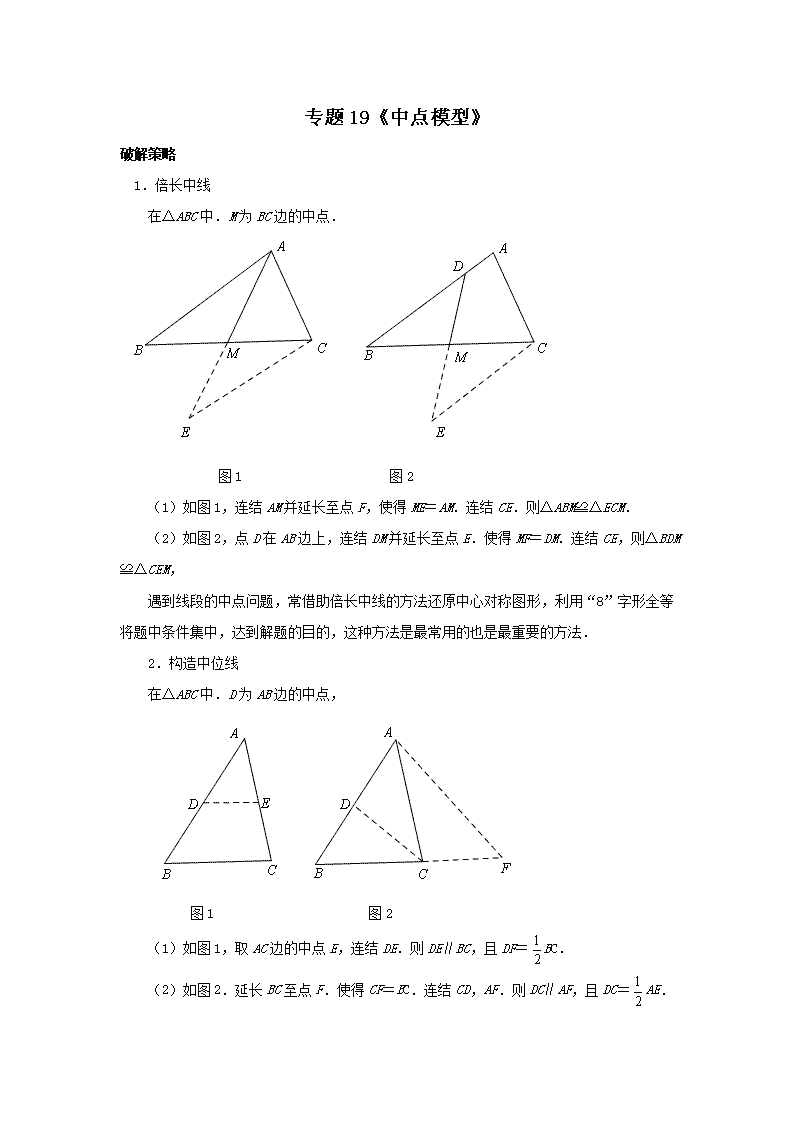
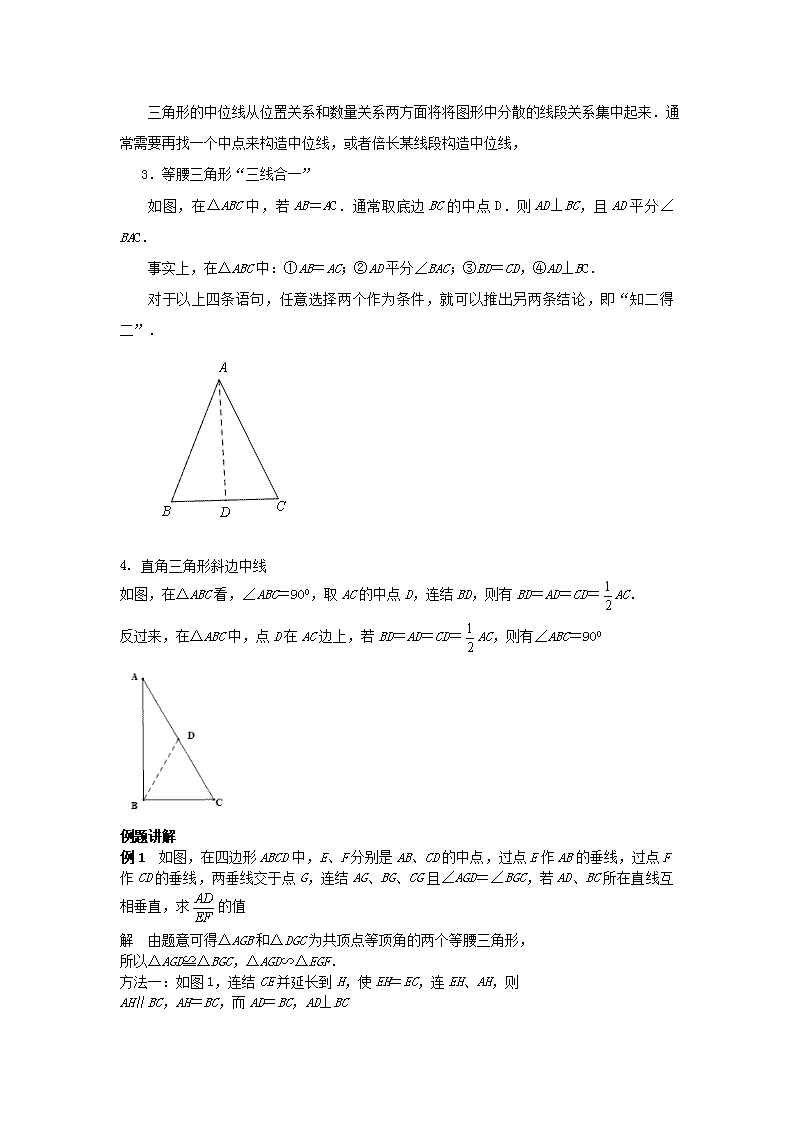
专题19《中点模型》‎ 破解策略 ‎1．倍长中线 ‎ 在△ABC中．M为BC边的中点．‎ ‎ ‎ 图1 图2‎ ‎ （1）如图1，连结AM并延长至点F，使得ME＝AM．连结CE．则△ABM≌△ECM．‎ ‎ （2）如图2，点D在AB边上，连结DM并延长至点E．使得MF＝DM．连结CE，则△BDM≌△CEM，‎ ‎ 遇到线段的中点问题，常借助倍长中线的方法还原中心对称图形，利用“8”字形全等将题中条件集中，达到解题的目的，这种方法是最常用的也是最重要的方法．‎ ‎ 2．构造中位线 ‎ 在△ABC中．D为AB边的中点，‎ ‎ ‎ 图1 图2‎ ‎ （1）如图1，取AC边的中点E，连结DE．则DE∥BC，且DF＝BC．‎ ‎ （2）如图2．延长BC至点F．使得CF＝BC．连结CD，AF．则DC∥AF，且DC＝AE．‎ ‎ 三角形的中位线从位置关系和数量关系两方面将将图形中分散的线段关系集中起来．通常需要再找一个中点来构造中位线，或者倍长某线段构造中位线，‎ ‎ 3．等腰三角形“三线合一”‎ ‎ 如图，在△ABC中，若AB＝AC．通常取底边BC的中点D．则AD⊥BC，且AD平分∠BAC．‎ ‎ 事实上，在△ABC中：①AB＝AC；②AD平分∠BAC；③BD＝CD，④AD⊥BC．‎ ‎ 对于以上四条语句，任意选择两个作为条件，就可以推出另两条结论，即“知二得二”．‎ ‎ ‎ 4. 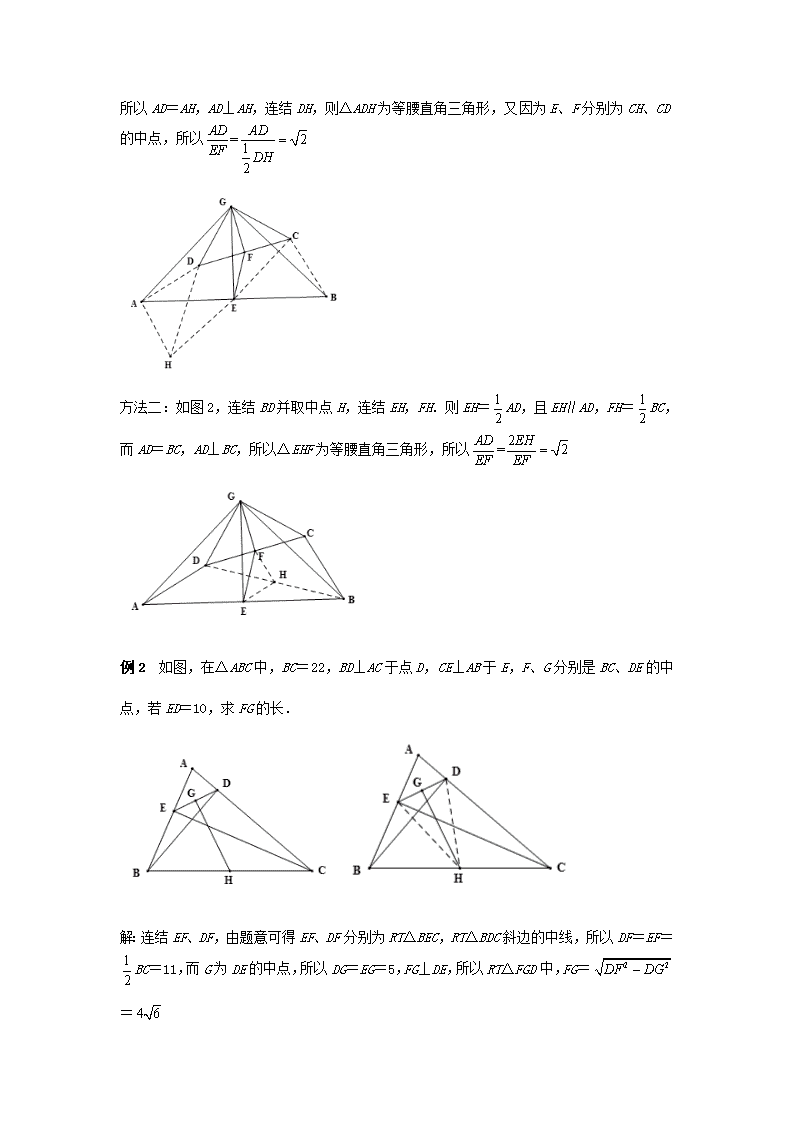直角三角形斜边中线 如图，在△ABC看，∠ABC＝900，取AC的中点D，连结BD，则有BD＝AD＝CD＝AC．‎ 反过来，在△ABC中，点D在AC边上，若BD＝AD＝CD＝AC，则有∠ABC＝900‎ 例题讲解 例1 如图，在四边形ABCD中，E、F分别是AB、CD的中点，过点E作AB的垂线，过点F作CD的垂线，两垂线交于点G，连结AG、BG、CG且∠AGD＝∠BGC，若AD、BC所在直线互相垂直，求的值 解 由题意可得△AGB和△DGC为共顶点等顶角的两个等腰三角形，‎ 所以△AGD≌△BGC，△AGD∽△EGF．‎ 方法一：如图1，连结CE并延长到H，使EH＝EC，连EH、AH，则 AH∥BC，AH＝BC，而AD＝BC，AD⊥BC 所以AD＝AH，AD⊥AH，连结DH，则△ADH为等腰直角三角形，又因为E、F分别为CH、CD的中点，所以 方法二：如图2，连结BD并取中点H，连结EH，FH．则EH＝AD，且EH∥AD，FH＝BC，‎ 而AD＝BC，AD⊥BC，所以△EHF为等腰直角三角形，所以 例2 如图，在△ABC中，BC＝22，BD⊥AC于点D，CE⊥AB于E，F、G分别是BC、DE的中点，若ED＝10，求FG的长．‎ 解：连结EF、DF，由题意可得EF、DF分别为RT△BEC，RT△BDC斜边的中线，所以DF＝EF＝BC＝11，而G为DE的中点，所以DG＝EG＝5，FG⊥DE，所以RT△FGD中，FG＝＝‎ 例3 已知：在RT△ACB和RT△AEF中，∠ACB＝∠AEF＝900，若P是BF的中点，连结PC、PE （1） 如图1，若点E、F分别落在边AB、AC上，请直接写出此时PC与PE的数量关系．‎ （2） 如图2，把图1中的△AEF绕着点A顺时针旋转，当点E落在边CA的延长线上时，上述结论是否成立？若成立，请给予证明；若不成立，请说明理由．‎ ‎（3）如图3，若点F落在边AB上，则上述结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．‎ 解（1）易得PC＝PE＝BF，即PC与PE相等．‎ ‎（2）结论成立．理由如下：‎ 如图4，延长CP交EF的延长线于点D，则BC∥FD，易证△BPC≌△FPD，所以PC＝PD，而∠CED＝900，所以PE＝CD＝PC （3） 结论仍成立，理由如下：‎ 如图5，过点F作FD∥BC，交CP的延长线于点D，易得PD＝PC，FD＝BC 所以 而∠AFE＝∠PBC＝∠PFD，所以∠EAC＝1800－2∠AFE＝∠EFD，‎ 如图，连结CE，ED，则△EAC∽△EFD，所以∠AEC＝∠FED，∠CED＝∠AEF＝900，‎ 所以PE＝CD＝PC 例4 已知：△ABC是等腰三角形，∠BAC＝900，DE⊥CE，DE＝CE＝AC，连结AE，M是AE的中点 （1） 如图1，若D在△ABC的内部，连结BD，N是BD的中点，连结MN，NE，求证：MN⊥AE （2） 如图2，将图1中的△CDE绕点C逆时针旋转，使∠BCD＝300，连结BD，N是BD的中点，连结MN，求 解：（1）如图3，延长EN至点F，使得NF＝NE，连结FB，易证△DEN≌△BFN，从而可得BF∥DE，BF＝DE，延长FB，CE交于点G，则∠G＝900，从而A、B、G、C四点共圆 所以∠ABF＝∠ACE，连结AF，所以△ABF≌△ACE（SAS），所以AF＝AE，AF⊥AE，而MN∥AF所以MN＝AE，MN⊥AE ‎（2）如图4，同（1）可得，MN＝AE，MN⊥AE，由题意可得AC＝2CE，作EH⊥AC于H，则∠ECH＝600，所以CH＝EC＝AC，EH＝AC，从而AE＝，所以 进阶训练 ‎1．如图，△ABD和△ACE都是直角三角形，其中∠ABD ＝∠ACE＝90°，且点C在 AB上，连结DE，M为DE的中点，连结BM，CM，求证：BM＝CM．‎ ‎ ‎ ‎ 【答案】略 ‎【提示】延长CM，DB交于点F，则∠CBF＝90°，△CME≌△FMD，从而BM＝CF＝CM．‎ ‎2．我们把两条中线互相垂直的三角形称为”中垂三角形”．如图1，AF，BE是△ABC的中线，且AF⊥BE于点P，像△ABC这样的三角形均称为“中垂三角形”，设BC＝a，AC＝b，AB＝c．‎ ‎ （1）猜想a 2，b2，c2三者之间的关系，并加以证明；‎ ‎ （2）如图2，在平行四边形ABCD中，E，F，G分别是AD，BC，CD上的中点．BE⊥EG，AD＝2，AB＝3．求AF的长．‎ ‎【答案】（1） a 2＋b2 ＝5c2，证明略；（2） AF＝4．‎ ‎【提示】（1）如图，连结EF，由中位线定理可得＝＝＝．在Rt△APB，Rt△APE和Rt△BPF中，利用勾股定理即可得到a 2＋b2 ＝5c2； ‎ ‎（2） 如图，取AB的中点H，连结FH，AC，由中位线定理可得FH∥AC∥EG，从而FH⊥BE，易证△APE≌△FPB，所以AP＝FP，所以△ABF是“中垂三角形”从而利用（1）中结论求得AF的长．‎ ‎3．巳知：△ABC和△ADE是等腰直角三角形，∠ACB＝∠ADE＝90°，F为BE的中点．连结DF，CF．‎ ‎ ‎ ‎（1）如图，当点D在AB上，点E在AC上时，请直接写出此时线段DF，CF的数量关系和位置关系（不用证明）；‎ ‎ （2）如图2．在（1）的条件下将△ADE绕点A顺时针旋转45°．请你判断此时（1）中的结论是否仍然成立，并证明你的判断； ‎ ‎ （3）如图3．在（1）的条件下将△ADE绕点A顺时针旋转角α，请你判断此时（1）中的结论是否仍然成立，井证明你的判断．‎ ‎【答案】（1）DF＝CF，DF⊥CF；（2）成立；（3）成立．‎ ‎【提示】（2）延长DF交BC于点G，则△DEF≌△GBF，从而得DF＝GF，CD＝CG，即得证．‎ ‎（3）延长CF至点G，使得FG＝CF，连结EG，则GE＝CB＝CA，GE⊥AC，可得∠CAD＝∠GED．连结DG，CD，从而△ADC≌△EDG（SAS）．即得证．‎ ‎4．巳知：P是平行四边形ABCD对角线AC所在直线上的一个动点（不与点A、C重合）．分别过点A、C向直线BP作垂线，垂足分别为E，F，O为AC的中点，如图1．将直线BP绕点B逆时针旋转，当∠OFE＝ 30°时，如图2所示，请你猜想线段CF，AE，OE之间有怎样的数量关系，并给予证明．‎ ‎【答案】图1中OE＝CF－AE；图2中OE＝CF＋AE．‎ ‎【提示】如图1，延长EO交FC于点G，易证OE＝OG，AE＝CG，从而Rt△GFE中，OF＝OG＝OE．而∠OFE＝30°，所以OE＝CF－AE．‎ 如图2，同理可得OE＝CF＋AE．‎