上海市数学中考真题含答案 16页

‎2017年上海市初中毕业统一学业考试 数学试卷 考生注意：‎ ‎1．本试卷共25题；‎ ‎2．试卷满分150分，考试时间100分钟 ‎3．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；‎ ‎4．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】‎ ‎1．下列实数中，无理数是 （ ）‎ ‎ A．0； B．； C．； D．‎ ‎2．下列方程中，没有实数根的是 （ ）‎ ‎ A．； B．； C．； D．．‎ ‎3．如果一次函数（、是常数，）的图像经过第一、二、四象限，那么k、b应满足的条件是 ‎ （ ）‎ ‎ A．，且； B．，且； C．，且； D．，且．‎ ‎4．数据2、5、6、0、6、1、8的中位数和众数分别是 （ ）‎ ‎ A．0和6； B．0和8； C．5和6； D．5和8．‎ ‎5．下列图形中，既是轴对称又是中心对称图形的是 （ ）‎ ‎ A．菱形； B．等边三角形； C．平行四边形； D．等腰梯形．‎ ‎6．已知平行四边形，、是它的两条对角线，那么下列条件中，能判断这个平行四边形为矩形的是 （ ）‎ ‎ A．； B．； C．； D．．‎ 二、填空题：（本大题共12题，每题4分，满分48分）‎ ‎ 【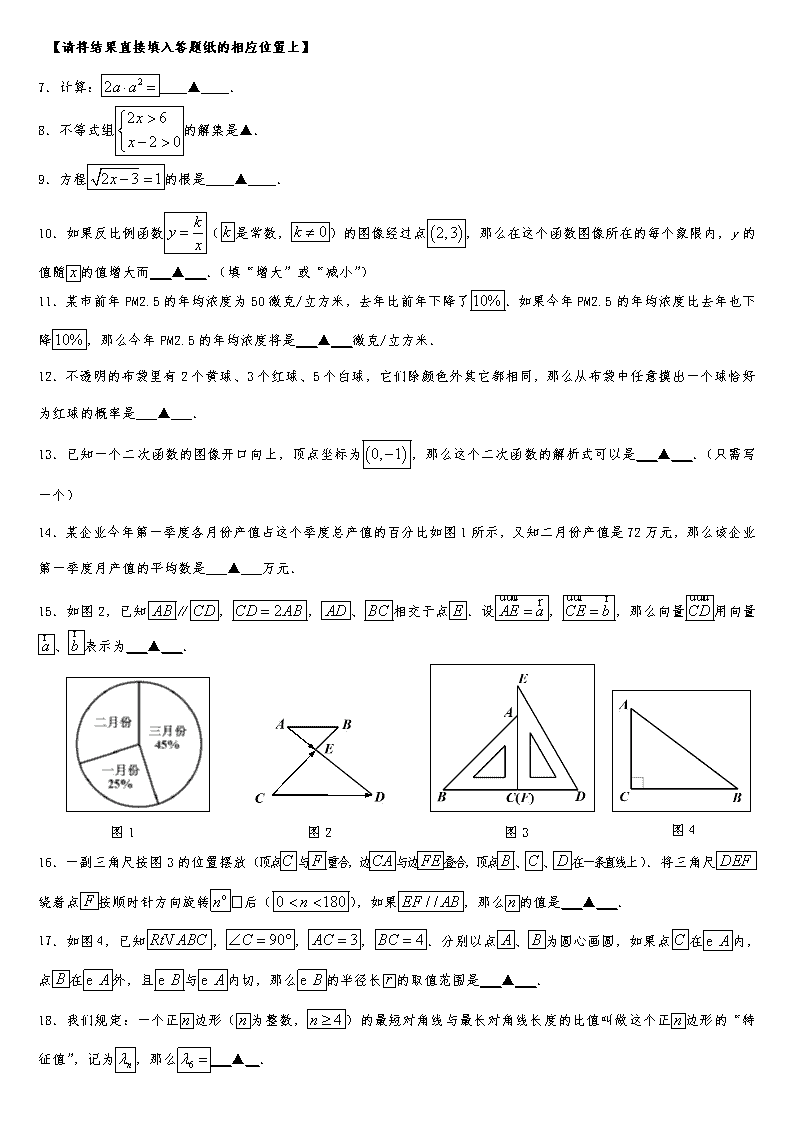请将结果直接填入答题纸的相应位置上】‎ ‎7．计算：____▲____．‎ ‎8．不等式组的解集是▲．‎ ‎9．方程的根是____▲____．‎ ‎10．如果反比例函数（是常数，）的图像经过点，那么在这个函数图像所在的每个象限内，y的值随的值增大而___▲___．（填“增大”或“减小”）‎ ‎11．某市前年PM2.5的年均浓度为50微克/立方米，去年比前年下降了．如果今年PM2.5的年均浓度比去年也下降，那么今年PM2.5的年均浓度将是___▲___微克/立方米．‎ ‎12．不透明的布袋里有2个黄球、3个红球、5个白球，它们除颜色外其它都相同，那么从布袋中任意摸出一个球恰好为红球的概率是___▲___．‎ ‎13．已知一个二次函数的图像开口向上，顶点坐标为，那么这个二次函数的解析式可以是___▲___．（只需写一个）‎ ‎14．某企业今年第一季度各月份产值占这个季度总产值的百分比如图1所示，又知二月份产值是72万元，那么该企业第一季度月产值的平均数是___▲___万元．‎ ‎15．如图2，已知∥，，、相交于点．设，，那么向量用向量、表示为___▲___．‎ ‎ ‎ ‎ 图1 图2 图3 图4‎ ‎16．一副三角尺按图3的位置摆放（顶点与重合，边与边叠合，顶点、、在一条直线上）．将三角尺绕着点按顺时针方向旋转 后（），如果，那么的值是___▲___．‎ ‎17．如图4，已知，，，．分别以点、为圆心画圆，如果点在内，点在外，且与内切，那么的半径长的取值范围是___▲___．‎ ‎18．我们规定：一个正边形（为整数，）的最短对角线与最长对角线长度的比值叫做这个正边形的“特征值”，记为，那么___▲__．‎ 三、解答题：（本大题共7题，满分78分）‎ ‎19．（本题满分10分）‎ 计算：‎ ‎20．（本题满分10分）‎ 解方程：‎ ‎21．（本题满分10分，第（1）小题满分4分，第（2）小题满分6分）‎ 如图5，一座钢结构桥梁的框架是，水平横梁长18米，中柱高6米，其中是的中点，且．‎ ‎（1）求的值；‎ ‎（2）现需要加装支架、，其中点在上，且，垂足为点．求支架的长．‎ ‎22．（本题满分10分，每小题满分各5分）‎ 甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案．甲公司方案：每月的养护费用y（元）与绿化面积x（平方米）是一次函数关系，如图6所示．乙公司方案：绿化面积不超过1000平方米时，每月收取费用5500元；绿化面积超过1000平方米时，每月在收取5500元的基础上，超过部分每平方米收取4元．‎ ‎（1）求图6所示的与的函数解析式；（不要求写出定义域）‎ ‎（2）如果某学校目前的绿化面积是1200平方米，试通过计算说明：选择哪家公司的服务，每月的绿化养护费用较少．‎ ‎23．（本题满分12分，第（1）小题满分7分，第（2）小题满分5分）‎ 已知：如图7，四边形中，，，是对角线BD上一点，且．‎ ‎（1）求证：四边形是菱形；‎ ‎（2）如果，且，求证：四边形是正方形．‎ ‎24．（本题满分12分，每小题满分各4分）‎ 已知在平面直角坐标系中（如图8），已知抛物线经过点，对称轴是直线，顶点为B．‎ ‎（1）求这条抛物线的表达式和点B的坐标；‎ ‎（2）点M在对称轴上，且位于顶点上方，设它的纵坐标为m，联结，用含的代数式表示的余切值；‎ ‎（3）将该抛物线向上或向下平移，使得新抛物线的顶点C在x轴上．原抛物线上一点P平移后的对应点为点Q，如果，求点的坐标．‎ ‎25．（本题满分14分，第（1）小题满分4分，第（2）小题满分5分，第（3）小题满分5分）‎ 如图9，已知的半径长为1，AB、AC是的两条弦，且，的延长线交于点，联结、．‎ ‎（1）求证：；‎ ‎（2）当是直角三角形时，求B、C两点的距离；‎ ‎（3）记、、的面积分别为、、，如果是和的比例中项，求的长．‎ ‎ ‎ ‎2017年上海市初中毕业统一学业考试 数学试卷参考答案 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎1、B；‎ 考察方向：基础概念。‎ 知识内容：本题考查无理数的定义，选项设置分别为“自然数/整数”、“无理数”、“负数/整数”、“分数”‎ ‎2、D；‎ 考察方向：基础知识和基本技能/理解初中数学有关基础知识 知识内容：方程与代数/一元二次方程根的判别式 方法：本题考查一元二次方程的根与判别式的关系。经计算，D选项：。‎ 本题也可通过配方的方式，得到答案。‎ ‎3、B；‎ 考察方向：基础概念，函数图像。‎ 方法：数形结合。‎ 知识内容：本题考查一次函数图像性质，经过二、四象限，可知，经过一、二象限，可知。‎ ‎4、C；‎ 考察方向：基础概念。‎ 方法：数据重排。‎ 知识内容：本题考查统计量基本概念，将数据重排：0，1，2，5，6，6，8，可看出中位数为，众数为。‎ 点评：A选项如果不进行重排，可作为干扰项；但如果本题能将D选项改成“6和5”，那就会从审题上进一步提高干扰难度（看错中位数和众数的顺序）。‎ ‎5、A；‎ 考察方向：基础概念。‎ 知识内容：本题考查轴对称基本概念，同时要求学生掌握各类四边形的基本形状特征。‎ ‎6、C；‎ 考察方向：几何图形性质判定。‎ 方法：直接法。‎ 知识内容：本题考查轴对称基本性质的应用--特殊的平行四边形，‎ A选项对任意平行四边形均成立；B选项可得到对角线评分一组对角，因此是菱形；C选项可判定对角线的一半相等，因此对角线相等，从而是矩形，正确。D选项比较有挑战性，若能用直接法判定C选项，D可直接跳过，而D选项，由可推知，∴，因此，在画图的时候，可先画线段BD，然后以B为圆心，为半径做圆，在圆上任取不与BD相交的点，都可作为A点，因此D无法断定为矩形。‎ 二、填空题：（本大题共12题，每题4分，满分48分）‎ ‎7、；‎ 考察方向：基础计算。‎ 知识内容：本题考查幂指数运算。‎ ‎8、；‎ 考察方向：基础计算。‎ 知识内容：本题考查不等式解法，以及通过数轴作图的方式得到不等式组最终答案。‎ ‎9、；‎ 考察方向：基础计算。‎ 知识内容：本题考查根式方程。‎ 点评：如果改为，既能考查根式方程，二次方程，又可以考查增根，考查效果会更好。‎ ‎10、减小；‎ 考察方向：基础概念及性质，概念计算。‎ 知识内容：本题考查反比例函数性质，概念计算，经过点，可知在1，3象限，故填“减小”。‎ ‎11、40.5；‎ 考察方向：百分比概念，数学建模，基础计算。‎ 知识内容：本题考查百分数的计算，认真审题之后，得到式子，即可得到答案。‎ 点评：结合实际问题，需要考生认真审题，理清三年之间的关系即可。‎ ‎12、；‎ 考察方向：基本概念，概率计算。‎ 知识内容：本题考查概率的计算，抽取1次，很基础的计算。‎ ‎13、等；‎ 考察方向：基础概念。‎ 知识内容：本题考查二次函数顶点式，由题意可设置二次函数顶点式，任取，即可。‎ ‎14、80；‎ 考察方向：统计饼状图，审题。‎ 知识内容：本题考查饼状图百分比计算，算出二月份占比30%，因此三个月总数240万，然后计算出一季度总产值108万，但此时特别注意问题“第一季度月产值的均值”，还要÷3．‎ ‎15、；‎ 考察方向：掌握向量加减基本方法。‎ 知识内容：本题考查平行线性质，实数与向量相乘的几何意义，向量的加减．综合性较好，适合在15题开始抬升难度梯度．‎ ‎16、；‎ 能力要求：空间观念/能进行几何图形的基本运动和变化 知识内容：图形与几何/平行线的判定和性质 点评：题中有限制条件，旋转角在0~180°之间。从某种程度上降低了一定难度；本题如果进一步改编，如果“”难度就可以上升到17题水平。相应解法使用“高”。‎ ‎17、；‎ 能力要求：空间观念/能够从复杂的图形中区分基本图形，并能分析其中的基本元素及其关系 知识内容：图形与几何/平行线的判定和性质 点评：题中有限制条件，旋转角在0~180°之间。从某种程度上降低了一定难度；本题如果进一步改编，如果“”难度就可以上升到17题水平。相应解法使用“高”。‎ 解析：设半径为，则 ‎18、；‎ 能力要求：解决简单问题的能力/初步掌握观察、操作、比较、类比、归纳的方法；懂得“从特殊到一般”、“从一般到 特殊”及“转化”等思维策略。‎ 知识内容：图形与几何/多边形及其有关概念，锐角三角比 点评：本题只需弄清概念即可，针对问题的情况，画图，然后明确角度，将提干的定义转化为合适的三角比，本题即可求解。‎ 解析：如图，在正六边形中，是一条最短的对角线，是一条最长的对角线.，，所以 三、解答题：（本大题共7题，满分78分）‎ ‎19．（本题满分10分）‎ 能力要求：基础知识和基本技能/能按照一定的规则和步骤进行计算 知识内容：数与运算/实数的运算；方程与代数/分数指数幂的概念和运算；方程与代数/二次根式的性质及运算 解析：原式 ‎20．（本题满分10分）‎ 能力要求：基础知识和基本技能/能按照一定的规则和步骤进行计算 知识内容：方程与代数/分式方程的解法 解析：去分母，得．‎ 移项、整理得．‎ 解方程，得，．‎ 经检验：是增根，舍去；是原方程的根．‎ 所以原方程的根是．‎ ‎19、20题点评：两道基础计算题，并没有特别大的变化，只需要保证计算的正确率和过程的完整性，就可以不失分。‎ ‎21．（本题满分10分，第（1）小题满分4分，第（2）小题满分6分）‎ 能力要求：‎ ‎（1）运算能力/知道有关算理，能根据问题条件，寻找和设计合理、有效的运算途径 ‎（2）运算能力/知道有关算理，能根据问题条件，寻找和设计合理、有效的运算途径 运算能力/能通过运算进行推理和探求 知识内容：‎ ‎（1）图形与几何/等腰三角形的性质 图形与几何/勾股定理 图形与几何/锐角三角比（锐角的正弦、余弦、正切、余切）的概念 ‎（2）图形与几何/画已知直线的垂线，尺规作线段的垂直平分线 图形与几何/勾股定理 解析：（1）∵是中点，，∴‎ 又∵，且，∴在中，‎ ‎∴‎ ‎（2）∵，∴．‎ ‎∵，，∴，∴，‎ 又∵，，∴，，∴‎ ‎∴在中，‎ ‎22．（本题满分10分，每小题满分各5分）‎ 能力要求：‎ ‎（1）解决简单问题的能力/知道一些基本的数学模型，并通过运用，解决一些简单的实际问题 ‎（2）基础知识与基本技能/能按照一定的规则和步骤进行计算 知识内容：‎ ‎（1）函数与分析/用待定系数法求一次函数的解析式 函数与分析/一次函数的应用 ‎（2）函数与分析/函数以及函数值等有关概念 解析：（1）设关于的函数解析式为 由题意，得，解得 ‎（2）设乙公司每个月收取费用为，由题意，。‎ 若，代入第（1）问，得甲公司方案费用：‎ 代入的解析式，得乙公司方案费用：‎ ‎∴选择乙公司的服务，每月的绿化养护费用较少．‎ 点评：第二问中关于乙公司的函数关系，需要用分段函数的表示，然后利用函数值的大小比较得到最终的答案。‎ ‎23．（本题满分12分，第（1）小题满分7分，第（2）小题满分5分）‎ 能力要求：‎ ‎（1）逻辑推理能力/能简明和有条理地表述演绎推理过程，合理解释推理演绎的正确性 ‎（2）空间观念/能够从复杂的图形中区分基本图形，并能分析其中的基本元素及其关系 知识内容：‎ ‎（1）图形与几何/平行四边形的判定和性质 图形与几何/等腰三角形的性质 图形与几何/菱形的判定和性质 ‎（2）图形与几何/等腰三角形的性质 图形与几何/三角形的内角和 图形与几何/正方形的判定 解析：（1）∵，∴,‎ ‎∴‎ 又∵,∴,‎ ‎∴,∴,‎ ‎∴,又∴四边形是平行四边形 又,∴是菱形，即证 ‎（2）∵，∴是等腰三角形，∴‎ ‎∵，∴设，则 在△中，，∴．‎ ‎∵四边形是菱形，∴平分，∴‎ ‎∴菱形是正方形 点评：23题证明并未涉及相似的知识点，仅考察八年级下内容，题目较为简单。‎ ‎24．（本题满分12分，每小题满分各4分）‎ 能力要求：‎ ‎（1）基础知识和基本技能/能按照一定的规则和步骤进行计算、画（作）图 ‎（2）基础知识和基本技能/能按照一定的规则和步骤进行计算、画（作）图 运算能力/知道有关算理，能根据问题条件，寻找和设计合理、有效的运算途径 ‎（3）逻辑推理能力/能简明和有条理地表述演绎推理过程，合理解释推理演绎的正确性 基础知识和基本技能/能按照一定的规则和步骤进行计算、画（作）图 知识内容：‎ ‎（1）函数与分析/待定系数法求二次函数解析式 函数与分析/函数值等有关概念 ‎ ‎（2）图形与几何/锐角三角比的概念 图形与几何/平面直角坐标系的有关概念 ‎（3）图形与几何/直角坐标平面上点的平移、对称以及简单图形的对称问题 函数与分析/函数值等有关概念 解析：‎ ‎（1）对称轴 ，代入点，得.‎ 所以抛物线的解析式为.‎ 配方得：，所以顶点的坐标为.‎ ‎（2）过点向抛物线的对称轴作垂线，垂足为.则 在Rt△中，，，‎ 所以．‎ ‎（3）原抛物线向下平移后得到的新抛物线的解析式为.‎ 由题意可设 ，因为、两点的横坐标相同，当时， ‎ ‎、两点的纵坐标互为相反数，所以 ， ‎ 所以. 解得或.‎ 所以点的坐标为，或 答案：（1）;‎ ‎（2）‎ ‎（3）或 ‎25．（本题满分14分，第（1）小题满分4分，第（2）小题满分5分，第（3）小题满分5分）‎ 能力要求：‎ 空间观念/能够从复杂的图形中区分基本图形，并能分析其中的基本元素及其关系。‎ 空间观念/能由基本图形的性质导出复杂图形的性质。‎ 逻辑推理能力/能简明和有条理地表述演绎推理过程，合理解释推理演绎的正确性 运算能力/能通过运算进行推理和探求。‎ 解决简单问题的能力/初步掌握观察、操作、比较、类比、归纳的方法；懂得“从特殊到一般”、“从一般到特殊”及“转化”等思维策略。‎ 知识内容：‎ ‎（1）图形与几何/圆的概念 图形与几何/相似三角形的判定和性质及其应用 ‎（2）图形与几何/等腰三角形的性质与判定 ‎（3）数与运算/比、比例和百分比的有关概念及比例的基本性质 方程与代数/一元二次方程的概念及解法 解析：‎ ‎（1）如图，因为，所以，.‎ 所以 因为弦，所以圆心角，所以.‎ 又因为，所以△△.‎ ‎（2）为直角三角形有两种情况：‎ ‎①如图，当时，，所以垂直平分，.‎ 所以△是等边三角形，是等边三角形的中心，此时.‎ ‎②如图，当时，△是等腰直角三角形，此时.‎ ‎（3）如图，因为，所以点到弦的距离相等 所以：‎ 当是和的比例中项时，即：‎ 所以点是线段的黄金分割点，‎ 所以，所以 ‎.‎ 答案：‎ ‎（1）证明见解析 ‎（2）或 ‎（3）‎