中考数学二模试卷含解析15 23页

山东省菏泽市东明县 2016 年中考数学二模试卷 一、选择题（本大题共 8 个小题，每小题 3 分，共 24 分，在每小题给出的四个选项 A、B、 C、D 中，只有一项是正确的，请把正确的选项填在答题卡的相应位置.） 1．﹣的相反数是（ ） A．﹣ B． C． D．﹣ 2．如图，下列说法错误的是（ ） A．若 a∥b，b∥c，则 a∥c B．若∠1=∠2，则 a∥c C．若∠3=∠2，则 b∥c D．若∠3+∠5=180°，则 a∥c 3．某校九年级（1）班全体学生 2015 年初中毕业体育考试的成绩统计如下表： 成绩（分） 35 39 42 44 45 48 50 人数（人） 2 5 6 6 8 7 6 根据上表中的信息判断，下列结论中错误的是（ ） A．该班一共有 40 名同学 B．该班学生这次考试成绩的众数是 45 分 C．该班学生这次考试成绩的中位数是 45 分 D．该班学生这次考试成绩的平均数是 45 分 4．由几个相同的小正方形搭成的一个几何体如图所示，这个几何体的主视图是（ ） A． B． C． D． 5．不等式组的解集在数轴上表示正确的是（ ） A． B． C． D． 6．如图，四边形 ABCD 是⊙O 的内接四边形，⊙O 的半径为 2，∠B=135°，则的长（ ） A．2π B．π C． D． 7．如图，M，N 两点在数轴上表示的数分别是 m，n，则下列式子中成立的是（ ） A．m+n＜0 B．﹣m＜﹣n C．|m|﹣|n|＞0 D．2+m＜2+n 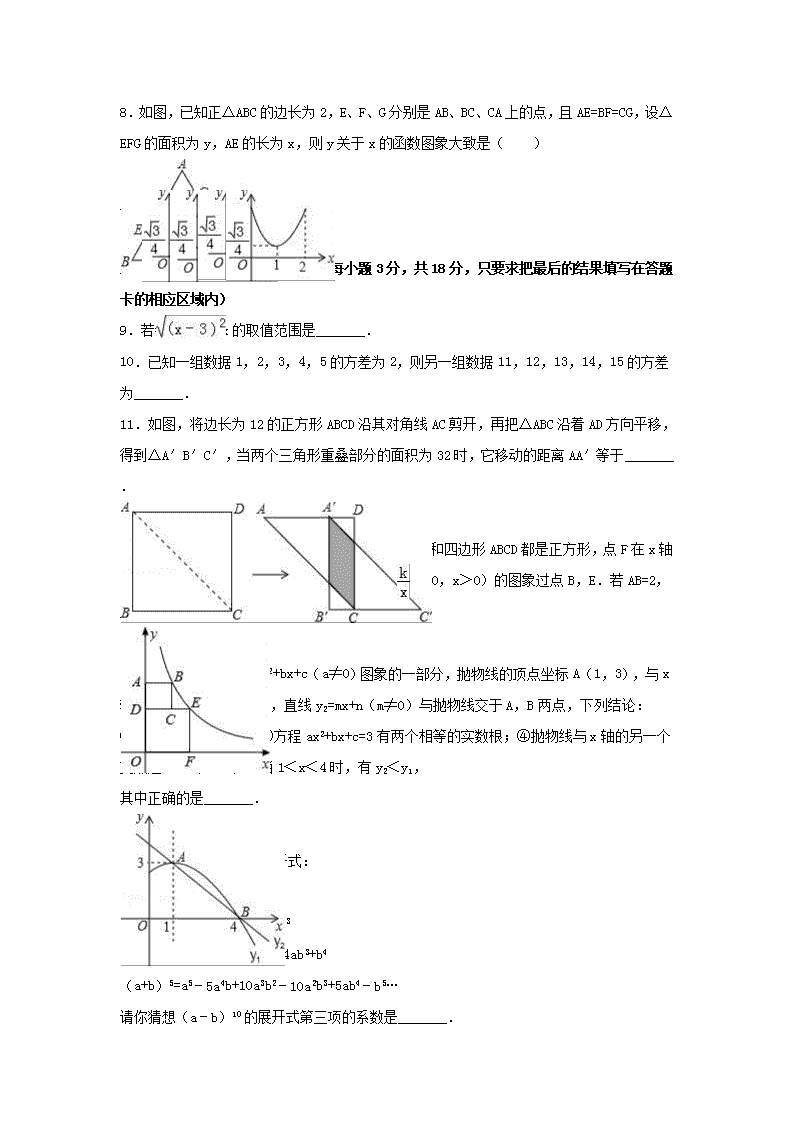8．如图，已知正△ABC 的边长为 2，E、F、G 分别是 AB、BC、CA 上的点，且 AE=BF=CG，设 △EFG 的面积为 y，AE 的长为 x，则 y 关于 x 的函数图象大致是（ ） A． B． C． D． 二、填空题（本大题共 6 个小题，每小题 3 分，共 18 分，只要求把最后的结果填写在答题 卡的相应区域内） 9．若=3﹣x，则 x 的取值范围是_______． 10．已知一组数据 1，2，3，4，5 的方差为 2，则另一组数据 11，12，13，14，15 的方差 为_______． 11．如图，将边长为 12 的正方形 ABCD 沿其对角线 AC 剪开，再把△ABC 沿着 AD 方向平移， 得到△A′B′C′，当两个三角形重叠部分的面积为 32 时，它移动的距离 AA′等于_______． 12．如图，在平面直角坐标系 xOy 中，四边形 ODEF 和四边形 ABCD 都是正方形，点 F 在 x 轴的正半轴上，点 C 在边 DE 上，反比例函数 y=（k≠0，x＞0）的图象过点 B，E．若 AB=2， 则 k 的值为_______． 13．如图是抛物线 y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标 A（1，3），与 x 轴的一个交点 B（4，0），直线 y2=mx+n（m≠0）与抛物线交于 A，B 两点，下列结论： ①2a+b=0；②abc＞0；③方程 ax2+bx+c=3 有两个相等的实数根；④抛物线与 x 轴的另一个 交点是（﹣1，0）；⑤当 1＜x＜4 时，有 y2＜y1， 其中正确的是_______． 14．观察下列各式及其展开式： （a+b）2=a2+2ab+b2 （a+b）3=a3﹣3a2b+3ab2﹣b3 （a+b）4=a4﹣4a3b+6a2b2﹣4ab3+b4 （a+b）5=a5﹣5a4b+10a3b2﹣10a2b3+5ab4﹣b5… 请你猜想（a﹣b）10 的展开式第三项的系数是_______． 三、解答题(本大题共 78 分) 15．计算：（﹣1）2015﹣+（3﹣π）0+|3﹣|+（tan30°）﹣1． 16．解方程：﹣=1． 17．如图，AB∥FC，D 是 AB 上一点，DF 交 AC 于点 E，DE=FE，分别延长 FD 和 CB 交于点 G． （1）求证：△ADE≌△CFE； （2）若 GB=2，BC=4，BD=1，求 AB 的长． 18．某物流公 司承接 A、B 两种货物运输业务，已知 5 月份 A 货物运费单价为 50 元/吨，B 货物运费单价为 30 元/吨，共收取运费 9500 元；6 月份由于油价上涨，运费单价上涨为：A 货物 70 元/吨，B 货物 40 元/吨；该物流公司 6 月承接的 A 种货物和 B 种数量与 5 月份相同， 6 月份共收取运费 13000 元． （1）该物流公司月运输两种货物各多少吨？ （2）该物流公司预计 7 月份运输这两种货物 330 吨，且 A 货物的数量不大于 B 货物的 2 倍， 在运费单价与 6 月份相同的情况下，该物流公司 7 月份最多将收到多少运输费？ 19．如图，在△ABC 中，AB=BC，BD 平分∠ABC．四边形 ABED 是平行四边形，DE 交 BC 于点 F， 连接 CE． 求证：四边形 BECD 是矩形． 20．如图，一次函数 y=kx+5（k 为常数，且 k≠0）的图象与反比例函数 y=﹣的函数交于 A （﹣2，b），B 两点． （1）求一次函数的表达式； （2）若将直线 AB 向下平移 m（m＞0）个单位长度后与反比例函数的图象有且只有一个公共 点，求 m 的值． 21．（10 分）（2015•安顺）如图，等腰三角形 ABC 中，AC=BC=10，AB=12，以 BC 为直径作 ⊙O 交 AB 于点 D，交 AC 于点 G，DF⊥AC，垂足为 F，交 CB 的延长线于点 E． （1）求证：直线 EF 是⊙O 的切线； （2）求 cos∠E 的值． 22．（10 分）（2015•东营）东营市为进一步加强和改进学校体育工作，切实提高学生体质 健康水平，决定推进“一校一球队、一级一专项、一人一技能”活动计划，某校决定对学生 感兴趣的球类项目（A：足球，B：篮球，C：排球，D：羽毛球，E：乒乓球）进行问卷调查， 学生可根据自己的喜好选修一门，李老师对某班全班同学的选课情况进行统计后，制成了两 幅不完整的统计图（如图） （1）将统计图补充完整； （2）求出该班学生人数； （3）若该校共用学生 3500 名，请估计有多少人选修足球？ （4）该班班委 5 人中，1 人选修篮球，3 人选修足球，1 人选修排球，李老师要从这 5 人中 任选 2 人了解他们对体育选修课的看法，请你用列表或画树状图的方法，求选出的 2 人恰好 1 人选修篮球，1 人选修足球的概率． 23．（10 分）（2015•东营）如图，两个全等的△ABC 和△DFE 重叠在一起，固定△ABC，将 △DEF 进行如下变换： （1）如图 1，△DEF 沿直线 CB 向右平移（即点 F 在线段 CB 上移动），连接 AF、AD、BD．请 直接写出 S△ABC 与 S 四边形 AFBD 的关系； （2）如图 2，当点 F 平移到线段 BC 的中点时，若四边形 AFBD 为正方形，那么△ABC 应满足 什么条件？请给出证明； （3）在（2）的条件下，将△DEF 沿 DF 折叠，点 E 落在 FA 的延长线上的点 G 处，连接 CG， 请你在图 3 的位置画出图形，并求出 sin∠CGF 的值． 24．（10 分）（2016•东明县二模）如图，在平面直角坐标系中，直线 y=﹣x+2 分别与 x 轴、 y 轴相交于点 B、C，经过点 B、C 的抛物线 y=﹣x2+bx+c 与 x 轴的另一个交点为 A（﹣1，0）． （1）求这个抛物线的解析式； （2）已知点 D 在抛物线上，且横坐标为 2，求出△BCD 的面积； （3）点 P 是直线 BC 上方的抛物线上一动点，过点 P 作 PQ 垂直于 x 轴，垂足为 Q．是否存 在点 P，使得以点 A、P、Q 为顶点的三角形与△BOC 相似？若存在，请求出点 P 的坐标；若 不存在，请说明理由． 2016 年山东省菏泽市东明县中考数学二模试卷 参考答案与试题解析 一、选择题（本大题共 8 个小题，每小题 3 分，共 24 分，在每小题给出的四个选项 A、B、 C、D 中，只有一项是正确的，请把正确的选项填在答题卡的相应位置.） 1．﹣的相反数是（ ） A．﹣ B． C． D．﹣ 【考点】相反数． 【分析】根据只有符号不同的两个数互为相反数，可得答案． 【解答】解：﹣的相反数是， 故选：C． 【点评】本题考查了相反数，在一个数的前面加上负号就是这个数的相反数． 2．如图，下列说法错误的是（ ） A．若 a∥b，b∥c，则 a∥c B．若∠1=∠2，则 a∥c C．若∠3=∠2，则 b∥c D．若∠3+∠5=180°，则 a∥c 【考点】平行线的判定． 【分析】根据平行线的判定进行判断即可． 【解答】解：A、若 a∥b，b∥c，则 a∥c，利用了平行公理，正确； B、若∠1=∠2，则 a∥c，利用了内错角相等，两直线平行，正确； C、∠3=∠2，不能判断 b∥c，错误； D、若∠3+∠5=180°，则 a∥c，利用同旁内角互补，两直线平行，正确； 故选 C． 【点评】此题考查平行线的判定，关键是根据几种平行线判定的方法进行分析． 3．某校九年级（1）班全体学生 2015 年初中毕业体育考试的成绩统计如下表： 成绩（分） 35 39 42 44 45 48 50 人数（人） 2 5 6 6 8 7 6 根据上表中的信息判断，下列结论中错误的是（ ） A．该班一共有 40 名同学 B．该班学生这次考试成绩的众数是 45 分 C．该班学生这次考试成绩的中位数是 45 分 D．该班学生这次考试成绩的平均数是 45 分 【考点】众数；统计表；加权平均数；中位数． 【分析】结合表格根据众数、平均数、中位数的概念求解． 【解答】解：该班人数为：2+5+6+6+8+7+6=40， 得 45 分的人数最多，众数为 45， 第 20 和 21 名同学的成绩的平均值为中位数，中位数为： =45， 平均数为： =44.425． 故错误的为 D． 故选 D． 【点评】本题考查了众数、平均数、中位数的知识，掌握各知识点的概念是解答本题的关键． 4．由几个相同的小正方形搭成的一个几何体如图所示，这个几何体的主视图是（ ） A． B． C． D． 【考点】简单组合体的三视图． 【分析】根据从正面看得到的视图是主视图，可得答案． 【解答】解：从正面看第一层是三个小正方形，第二层是靠右边两个小正方形， 故选：A． 【点评】本题考查了简单组合的三视图，从正面看得到的视图是主视图． 5．不等式组的解集在数轴上表示正确的是（ ） A． B． C． D． 【考点】在数轴上表示不等式的解集；解一元一次不等式组． 【分析】分别求出各不等式的解集，并在数轴上表示出来即可． 【解答】解：，由①得，x≤﹣1，由②得，x＞﹣5， 故﹣5＜x≤﹣1． 在数轴上表示为： ． 故选 A． 【点评】本题考查的是在数轴上表示不等式组的解集，熟知“小于向左，大于向右”是解答 此题的关键． 6．如图，四边形 ABCD 是⊙O 的内接四边形，⊙O 的半径为 2，∠B=135°，则的长（ ） A．2π B．π C． D． 【考点】弧长的计算；圆周角定理；圆内接四边形的性质． 【分析】连接 OA、OC，然后根据圆周角定理求得∠AOC 的度数，最后根据弧长公式求解． 【解答】解：连接 OA、OC， ∵∠B=135°， ∴∠D=180°﹣135°=45°， ∴∠AOC=90°， 则的长==π． 故选 B． 【点评】本题考查了弧长的计算以及圆周角定理，解答本题的关键是掌握弧长公式 L=． 7．如图，M，N 两点在数轴上表示的数分别是 m，n，则下列式子中成立的是（ ） A．m+n＜0 B．﹣m＜﹣n C．|m|﹣|n|＞0 D．2+m＜2+n 【考点】实数与数轴． 【分析】根据 M、N 两点在数轴上的位置判断出其取值范围，再对各选项进行逐一分析即可． 【解答】解：M、N 两点在数轴上的位置可知：﹣1＜m＜0，n＞2， ∵m+n＞O，故 A 错误， ∵﹣m＞﹣n，故 B 错误， ∵|m|﹣|n|＜0，故 C 错误． ∵2+m＜2+n 正确，故 D 正确． 故选：D． 【点评】本题考查的是数轴的特点，根据 a、b 两点在数轴上的位置判断出其取值范围是解 答此题的关键． 8．如图，已知正△ABC 的边长为 2，E、F、G 分别是 AB、BC、CA 上的点，且 AE=BF=CG，设 △EFG 的面积为 y，AE 的长为 x，则 y 关于 x 的函数图象大致是（ ） A． B． C． D． 【考点】动点问题的函数图象． 【分析】根据题意，易得△AEG、△BEF、△CFG 三个三角形全等，且在△AEG 中，AE=x，AG=2 ﹣x；可得△AEG 的面积 y 与 x 的关系；进而可判断出 y 关于 x 的函数的图象的大致形状． 【解答】解：根据题意，有 AE=BF=CG，且正三角形 ABC 的边长为 2， 故 BE=CF=AG=2﹣x； 故△AEG、△BEF、△CFG 三个三角形全等． 在△AEG 中，AE=x，AG=2﹣x． 则 S△AEG=AE×AG×sinA=x（2﹣x）； 故 y=S△ABC﹣3S△AEG =﹣3×x（2﹣x）=（3x2﹣6x+4）． 故可得其大致图象应类似于抛物线，且抛物线开口方向向上； 故选：D． 【点评】本题考查动点问题的函数图象问题，用图象解决问题时，要理清图象的含义即会识 图． 二、填空题（本大题共 6 个小题，每小题 3 分，共 18 分，只要求把最后的结果填写在答题 卡的相应区域内） 9．若=3﹣x，则 x 的取值范围是 x≤3 ． 【考点】二次根式的性质与化简． 【分析】根据二次根式的性质得出 3﹣x≥0，求出即可． 【解答】解：∵ =3﹣x， ∴3﹣x≥0， 解得：x≤3， 故答案为：x≤3． 【点评】本题考查了二次根式的性质的应用，注意：当 a≥0 时， =a，当 a＜0 时， =﹣a． 10．已知一组数据 1，2，3，4，5 的方差为 2，则另一组数据 11，12，13，14，15 的方差 为 2 ． 【考点】方差． 【分析】根据方差的性质，当一组数据同时加减一个数时方差不变，进而得出答案． 【解答】解：∵一组数据 1，2，3，4，5 的方差为 2， ∴则另一组数据 11，12，13，14，15 的方差为 2． 故答案为：2． 【点评】此题主要考查了方差的性质，正确记忆方差的有关性质是解题关键． 11．如图，将边长为 12 的正方形 ABCD 沿其对角线 AC 剪开，再把△ABC 沿着 AD 方向平移， 得到△A′B′C′，当两个三角形重叠部分的面积为 32 时，它移动的距离 AA′等于 4 或 8 ． 【考点】平移的性质；解一元二次方程-因式分解法；平行四边形的判定与性质；正方形的 性质． 【分析】根据平移的性质，结合阴影部分是平行四边形，△AA′H 与△HCB′都是等腰直角 三角形，则若设 AA′=x，则阴影部分的底长为 x，高 A′D=12﹣x，根据平行四边形的面积 公式即可列出方程求解． 【解答】解：设 AC 交 A′B′于 H， ∵∠A=45°，∠D=90° ∴△A′HA 是等腰直角三角形 设 AA′=x，则阴影部分的底长为 x，高 A′D=12﹣x ∴x•（12﹣x）=32 ∴x=4 或 8， 即 AA′=4 或 8cm． 故答案为：4 或 8． 【点评】考查了平移的性质及一元二次方程的解法等知识，解决本题关键是抓住平移后图形 的特点，利用方程方法解题． 12．如图，在平面直角坐标系 xOy 中，四边形 ODEF 和四边形 ABCD 都是正方形，点 F 在 x 轴的正半轴上，点 C 在边 DE 上，反比例函数 y=（k≠0，x＞0）的图象过点 B，E．若 AB=2， 则 k 的值为 6+2 ． 【考点】反比例函数图象上点的坐标特征． 【分析】设 E（x，x），则 B（2，x+2），根据反比例函数系数的几何意义得出 x2=2（x+2）， 求得 E 的坐标，从而求得 k 的值． 【解答】解：设 E（x，x）， ∴B（2，x+2）， ∵反比例函数 y=（k≠0，x＞0）的图象过点 B、E． ∴x2=2（x+2）， 解得 x1=1+，x2=1﹣（舍去）， ∴k=x2=6+2， 故答案为 6+2． 【点评】本题考查了反比例函数图象上点的坐标特征，关键是掌握反比例函数图象上点与反 比例函数中系数 k 的关系． 13．如图是抛物线 y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标 A（1，3），与 x 轴的一个交点 B（4，0），直线 y2=mx+n（m≠0）与抛物线交于 A，B 两点，下列结论： ①2a+b=0；②abc＞0；③方程 ax2+bx+c=3 有两个相等的实数根；④抛物线与 x 轴的另一个 交点是（﹣1，0）；⑤当 1＜x＜4 时，有 y2＜y1， 其中正确的是 ①③⑤ ． 【考点】二次函数图象与系数的关系；抛物线与 x 轴的交点． 【分析】利用对称轴是直线 x=1 判定①；利用开口方向，对称轴与 y 轴的交点判定 a、b、c 得出②；利用顶点坐标和平移的规律判定③；利用对称轴和二次函数的对称性判定④；利用 图象直接判定⑤即可． 【解答】解：∵对称轴 x=﹣=1， ∴2a+b=0，①正确； ∵a＜0， ∴b＞0， ∵抛物线与 y 轴的交点在正半轴上， ∴c＞0， ∴abc＜0，②错误； ∵把抛物线 y=ax2+bx+c 向下平移 3 个单位，得到 y=ax2+bx+c﹣3， ∴顶点坐标 A（1，3）变为（1，0），抛物线与 x 轴相切， ∴方程 ax2+bx+c=3 有两个相等的实数根，③正确； ∵对称轴是直线 x=1，与 x 轴的一个交点是（4，0）， ∴与 x 轴的另一个交点是（﹣2，0），④错误； ∵当 1＜x＜4 时，由图象可知 y2＜y1， ∴⑤正确． 正确的有①③⑤． 故答案为：①③⑤． 【点评】本题考查了二次函数图象与系数的关系：对于二次函数 y=ax2+bx+c（a≠0），当 a ＞0 时，抛物线向上开口；当 a＜0 时，抛物线向下开口；一次项系数 b 和二次项系数 a 共 同决定对称轴的位置：当 a 与 b 同号时（即 ab＞0），对称轴在 y 轴左； 当 a 与 b 异号时 （即 ab＜0），对称轴在 y 轴右；常数项 c 决定抛物线与 y 轴交点，抛物线与 y 轴交于（0， c）；抛物线与 x 轴交点个数由△决定：△=b2﹣4ac＞0 时，抛物线与 x 轴有 2 个交点；△=b2 ﹣4ac=0 时，抛物线与 x 轴有 1 个交点；△=b2﹣4ac＜0 时，抛物线与 x 轴没有交点． 14．观察下列各式及其展开式： （a+b）2=a2+2ab+b2 （a+b）3=a3﹣3a2b+3ab2﹣b3 （a+b）4=a4﹣4a3b+6a2b2﹣4ab3+b4 （a+b）5=a5﹣5a4b+10a3b2﹣10a2b3+5ab4﹣b5… 请你猜想（a﹣b）10 的展开式第三项的系数是 45 ． 【考点】完全平方公式． 【分析】根据各式与展开式系数规律，确定出所求展开式第三项系数即可． 【解答】解：根据题意得：第五个式子系数为 1，6，15，20，15，6，1， 第六个式子系数为 1，7，21，35，35，21，7，1， 第七个式子系数为 1，8，28，56，70，56，28，8，1， 第八个式子系数为 1，9，36，84，126，126，84，36，9，1， 第九个式子系数为 1，10，45，120，210，252，210，120，45，10，1， 则（a﹣b）10 的展开式第三项的系数是 45， 故答案为：45． 【点评】此题考查了完全平方公式，弄清题中的规律是解本题的关键． 三、解答题(本大题共 78 分) 15．计算：（﹣1）2015﹣+（3﹣π）0+|3﹣|+（tan30°）﹣1． 【考点】实数的运算；零指数幂；负整数指数幂；特殊角的三角函数值． 【分析】原式利用乘方的意义，算术平方根定义，零指数幂、负整数指数幂法则，以及绝对 值的代数意义化简，计算即可得到结果． 【解答】解：原式=﹣1﹣3+1+3﹣+ =0． 【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键． 16．解方程：﹣=1． 【考点】解分式方程． 【分析】分式方程去分母转化为整式方程，求出整式方程的解得到 x 的值，经检验即可得到 分式方程的解． 【解答】解：去分母得：x2﹣3x+3=x2﹣x， 移项合并得：2x=3， 解得：x=， 经检验 x=是分式方程的解． 【点评】此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化 为整式方程求解．解分式方程一定注意要验根． 17．如图，AB∥FC，D 是 AB 上一点，DF 交 AC 于点 E，DE=FE，分别延长 FD 和 CB 交于点 G． （1）求证：△ADE≌△CFE； （2）若 GB=2，BC=4，BD=1，求 AB 的长． 【考点】相似三角形的判定与性质；全等三角形的判定与性质． 【分析】（1）由平行线的性质可得：∠A=∠FCE，再根据对顶角相等以及全等三角形的判定 方法即可证明：△ADE≌△CFE； （2）由 AB∥FC，可证明△GBD∽△GCF，根据给出的已知数据可求出 CF 的长，即 AD 的长， 进而可求出 AB 的长． 【解答】（1）证明：∵AB∥FC， ∴∠A=∠FCE， 在△ADE 和△CFE 中， ， ∴△ADE≌△CFE（AAS）； （2）解：∵AB∥FC， ∴△GBD∽△GCF， ∴GB：GC=BD：CF， ∵GB=2，BC=4，BD=1， ∴2：6=1：CF， ∴CF=3， ∵AD=CF， ∴AB=AD+BD=4． 【点评】本题考查了全等三角形的判定和性质、相似三角形的判定和性质以及平行线的性质， 题目的设计很好，难度一般． 18．某物流公 司承接 A、B 两种货物运输业务，已知 5 月份 A 货物运费单价为 50 元/吨，B 货物运费单价为 30 元/吨，共收取运费 9500 元；6 月份由于油价上涨，运费单价上涨为：A 货物 70 元/吨，B 货物 40 元/吨；该物流公司 6 月承接的 A 种货物和 B 种数量与 5 月份相同， 6 月份共收取运费 13000 元． （1）该物流公司月运输两种货物各多少吨？ （2）该物流公司预计 7 月份运输这两种货物 330 吨，且 A 货物的数量不大于 B 货物的 2 倍， 在运费单价与 6 月份相同的情况下，该物流公司 7 月份最多将收到多少运输费？ 【考点】一次函数的应用；二元一次方程组的应用；一元一次不等式的应用． 【分析】（1）设 A 种货物运输了 x 吨，设 B 种货物运输了 y 吨，根据题意可得到一个关于 x 的不等式组，解方程组求解即可； （2）运费可以表示为 x 的函数，根据函数的性质，即可求解． 【解答】解：（1）设 A 种货物运输了 x 吨，设 B 种货物运输了 y 吨， 依题意得：， 解之得：． 答：物流公司月运输 A 种货物 100 吨，B 种货物 150 吨． （2）设 A 种货物为 a 吨，则 B 种货物为（330﹣a）吨， 依题意得：a≤（330﹣a）×2， 解得：a≤220， 设获得的利润为 W 元，则 W=70a+40（330﹣a）=30a+13200， 根据一次函数的性质，可知 W 随着 a 的增大而增大 当 W 取最大值时 a=220， 即 W=19800 元． 所以该物流公司 7 月份最多将收到 19800 元运输费． 【点评】本题考查二元一次方程组的应用和一元一次不等式组以及一次函数性质的应用，将 现实生活中的事件与数学思想联系起来，读懂题意列出方程组和不等式即可求解． 19．如图，在△ABC 中，AB=BC，BD 平分∠ABC．四边形 ABED 是平行四边形，DE 交 BC 于点 F， 连接 CE． 求证：四边形 BECD 是矩形． 【考点】矩形的判定． 【分析】根据已知条件易推知四边形 BECD 是平行四边形．结合等腰△ABC“三线合一”的性 质证得 BD⊥AC，即∠BDC=90°，所以由“有一内角为直角的平行四边形是矩形”得到▱ BECD 是矩形． 【解答】证明：∵AB=BC，BD 平分∠ABC， ∴BD⊥AC，AD=CD． ∵四边形 ABED 是平行四边形， ∴BE∥AD，BE=AD， ∴BE=CD， ∴四边形 BECD 是平行四边形． ∵BD⊥AC， ∴∠BDC=90°， ∴▱ BECD 是矩形． 【点评】本题考查了矩形的判定．矩形的定义：有一个角是直角的平行四边形是矩形． 20．如图，一次函数 y=kx+5（k 为常数，且 k≠0）的图象与反比例函数 y=﹣的函数交于 A （﹣2，b），B 两点． （1）求一次函数的表达式； （2）若将直线 AB 向下平移 m（m＞0）个单位长度后与反比例函数的图象有且只有一个公共 点，求 m 的值． 【考点】反比例函数与一次函数的交点问题；一次函数图象与几何变换． 【分析】（1）先利用反比例函数解析式 y=﹣求出 b=4，得到 A 点坐标为（﹣2，4），然后 把 A 点坐标代入 y=kx+5 中求出 k，从而得到一次函数解析式为 y=x+5； （2）由于将直线 AB 向下平移 m（m＞0）个单位长度得直线解析式为 y=x+5﹣m，则直线 y=x+5 ﹣m 与反比例函数有且只有一个公共点，即方程组只有一组解， 然后消去 y 得到关于 x 的一元二次函数，再根据判别式的意义得到关于 m 的方程，最后解方 程求出 m 的值． 【解答】解：（1）把 A（﹣2，b）代入 y=﹣得 b=﹣=4， 所以 A 点坐标为（﹣2，4）， 把 A（﹣2，4）代入 y=kx+5 得﹣2k+5=4，解得 k=， 所以一次函数解析式为 y=x+5； （2）将直线 AB 向下平移 m（m＞0）个单位长度得直线解析式为 y=x+5﹣m， 根据题意方程组只有一组解， 消去 y 得﹣=x+5﹣m， 整理得 x2﹣（m﹣5）x+8=0， △=（m﹣5）2﹣4××8=0，解得 m=9 或 m=1， 即 m 的值为 1 或 9． 【点评】本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐 标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两 者无交点．也考查了一次函数与几何变换． 21．（10 分）（2015•安顺）如图，等腰三角形 ABC 中，AC=BC=10，AB=12，以 BC 为直径作 ⊙O 交 AB 于点 D，交 AC 于点 G，DF⊥AC，垂足为 F，交 CB 的延长线于点 E． （1）求证：直线 EF 是⊙O 的切线； （2）求 cos∠E 的值． 【考点】切线的判定；勾股定理． 【分析】（1）求证直线 EF 是⊙O 的切线，只要连接 OD 证明 OD⊥EF 即可； （2）根据∠E=∠CBG，可以把求 cos∠E 的值得问题转化为求 cos∠CBG，进而转化为求 Rt △BCG 中，两边的比的问题． 【解答】（1）证明：如图， 方法 1：连接 OD、CD． ∵BC 是直径， ∴CD⊥AB． ∵AC=BC． ∴D 是 AB 的中点． ∵O 为 CB 的中点， ∴OD∥AC． ∵DF⊥AC， ∴OD⊥EF． ∴EF 是 O 的切线． 方法 2：∵AC=BC， ∴∠A=∠ABC， ∵OB=OD， ∴∠DBO=∠BDO， ∵∠A+∠ADF=90° ∴∠EDB+∠BDO=∠A+∠ADF=90°． 即∠EDO=90°， ∴OD⊥ED ∴EF 是 O 的切线． （2）解：连 BG． ∵BC 是直径， ∴∠BDC=90°． ∴CD==8． ∵AB•CD=2S△ABC=AC•BG， ∴BG===． ∴CG==． ∵BG⊥AC，DF⊥AC， ∴BG∥EF． ∴∠E=∠CBG， ∴cos∠E=cos∠CBG==． 【点评】本题考查的是切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心 和这点（即为半径），再证垂直即可． 22．（10 分）（2015•东营）东营市为进一步加强和改进学校体育工作，切实提高学生体质 健康水平，决定推进“一校一球队、一级一专项、一人一技能”活动计划，某校决定对学生 感兴趣的球类项目（A：足球，B：篮球，C：排球，D：羽毛球，E：乒乓球）进行问卷调查， 学生可根据自己的喜好选修一门，李老师对某班全班同学的选课情况进行统计后，制成了两 幅不完整的统计图（如图） （1）将统计图补充完整； （2）求出该班学生人数； （3）若该校共用学生 3500 名，请估计有多少人选修足球？ （4）该班班委 5 人中，1 人选修篮球，3 人选修足球，1 人选修排球，李老师要从这 5 人中 任选 2 人了解他们对体育选修课的看法，请你用列表或画树状图的方法，求选出的 2 人恰好 1 人选修篮球，1 人选修足球的概率． 【考点】列表法与树状图法；用样本估计总体；扇形统计图；条形统计图． 【分析】（1）、（2）先利用 B 的人数和所占的百分比计算出全班人数，再利用 C、E 的百 分比计算出 C、E 的人数，则用全班人数分别减去 B、C、D、E 的人数得到 A 的人数，然后计 算 A、D 所占百分比； （3）根据样本估计总体，用 40%表示全校学生对足球感兴趣的百分比，然后用 3500 乘以 40% 即可得到选修足球的人数； （4）先利用树状图展示所有 20 种等可能的结果数，找出选出的 2 人恰好 1 人选修篮球，1 人选修足球所占结果数，然后根据概率公式求解． 【解答】解：（1）∵该班人数为 8÷16%=50（人）， ∴C 的人数=24%×50=12（人），E 的人数=8%×50=4（人）， ∴A 的人数=50﹣8﹣12﹣4﹣6=20（人）， A 所占的百分比=×100%=40%，D 所占的百分比=×100%=12%， 如图， （2）由（1）得该班学生人数为 50 人； （3）3500×40%=1400（人）， 估计有 1400 人选修足球； （4）画树状图： 共有 20 种等可能的结果数，其中选出的 2 人恰好 1 人选修篮球，1 人选修足球占 6 种， 所以选出的 2 人恰好 1 人选修篮球，1 人选修足球的概率==． 【点评】本题考查了列表法与树状图法：通过列表法或树状图法展示所有可能的结果求出 n， 再从中选出符合事件 A 或 B 的结果数目 m，然后利用概率公式求事件 A 或 B 的概率．也考查 了样本估计总体、扇形统计图和条形统计图． 23．（10 分）（2015•东营）如图，两个全等的△ABC 和△DFE 重叠在一起，固定△ABC，将 △DEF 进行如下变换： （1）如图 1，△DEF 沿直线 CB 向右平移（即点 F 在线段 CB 上移动），连接 AF、AD、BD．请 直接写出 S△ABC 与 S 四边形 AFBD 的关系； （2）如图 2，当点 F 平移到线段 BC 的中点时，若四边形 AFBD 为正方形，那么△ABC 应满足 什么条件？请给出证明； （3）在（2）的条件下，将△DEF 沿 DF 折叠，点 E 落在 FA 的延长线上的点 G 处，连接 CG， 请你在图 3 的位置画出图形，并求出 sin∠CGF 的值． 【考点】几何变换综合题． 【分析】（1）利用平行线的性质以及三角形面积关系得出答案； （2）利用平行四边形的判定得出四边形 AFBD 为平行四边形，进而得出 AF=BC=BF，求出答 案； （3）根据题意画出图形，利用 sin∠CGF=求出即可． 【解答】解：（1）S△ABC=S 四边形 AFBD， 理由：由题意可得：AD∥EC， 则 S△ADF=S△ABD， 故 S△ACF=S△ADF=S△ABD， 则 S△ABC=S 四边形 AFBD； （2）△ABC 为等腰直角三角形，即：AB=AC，∠BAC=90°， 理由如下：∵F 为 BC 的中点， ∴CF=BF， ∵CF=AD， ∴AD=BF， 又∵AD∥BF， ∴四边形 AFBD 为平行四边形， ∵AB=AC，F 为 BC 的中点， ∴AF⊥BC， ∴平行四边形 AFBD 为矩形， ∵∠BAC=90°，F 为 BC 的中点， ∴AF=BC=BF， ∴四边形 AFBD 为正方形； （3）如图 3 所示： 由（2）知，△ABC 为等腰直角三角形，AF⊥BC， 设 CF=k，则 GF=EF=CB=2k， 由勾股定理得：CG=k， sin∠CGF===． 【点评】此题主要考查了正方形的判定以及等腰直角三角形的性质和锐角三角函数关系等知 识，熟练应用正方形的判定方法是解题关键． 24．（10 分）（2016•东明县二模）如图，在平面直角坐标系中，直线 y=﹣x+2 分别与 x 轴、 y 轴相交于点 B、C，经过点 B、C 的抛物线 y=﹣x2+bx+c 与 x 轴的另一个交点为 A（﹣1，0）． （1）求这个抛物线的解析式； （2）已知点 D 在抛物线上，且横坐标为 2，求出△BCD 的面积； （3）点 P 是直线 BC 上方的抛物线上一动点，过点 P 作 PQ 垂直于 x 轴，垂足为 Q．是否存 在点 P，使得以点 A、P、Q 为顶点的三角形与△BOC 相似？若存在，请求出点 P 的坐标；若 不存在，请说明理由． 【考点】二次函数综合题． 【分析】（1）本题需先根据直线过 B，C 两点，求得 B，C 的坐标，然后根据的东西是即可 得出抛物线的解析式． （2）把 D 的横坐标代入抛物线的解析式求得纵坐标，求得四边形 OBDC 是梯形，可直接根据 三角形面积公式求得； （3）本题首先判断出存在，首先设点 P 的横坐标为 m，则 P 的纵坐标为﹣m2+m+2，再分两种 情况进行讨论：当==时和当==时，得出△APQ∽△BCO，△APQ∽△CBO，分别求出点 P 的坐标 即可． 【解答】解：（1）∵直线 y=﹣x+2 分别与 x 轴、y 轴相交于点 B、C， ∴B（3，0），C（0，2）， 将 A（﹣1，0），C（0，2）代入 y=﹣x2+bx+c 得， ， 解得． 故此抛物线的解析式为 y=﹣x2+x+2． （2）∵点 D 在抛物线上，且横坐标为 2， ∴y=﹣×22+×2+2=2， ∴D（2，2）， ∵C（0，2）， ∴CD∥AB， ∴四边形 OBDC 是梯形， ∴S△BCD=CD•OC=×2×2=2； （2）存在． 如图，设点 P 的横坐标为 m，则 P 的纵坐标为﹣m2+m+2， AQ=m+1，PQ=﹣m2+m+2， 又∵∠COB=∠PQA=90°， ∴①当==时， △APQ∽△BCO， 即 2（m+1）=3（﹣m2+m+2） 解得：m1=2，m2=﹣1（舍去）， 则 P（2，2）， ②当==时， △APQ∽△CBO， 即 3（m+1）=2（﹣m2+m+2）， 解得：m1=﹣1（不合题意，舍去），m2=， 则 P（，）． 故符合条件的点 P 的坐标为 P（2，2）或（，）． 【点评】本题考查了抛物线解析式的求法，相似三角形的问题，坐标系里表示三角形的面积 问题，要求会用字母代替长度，坐标，会对代数式进行合理变形．