中考数学上海市浦东新区第一学期九年级数学期中试卷 9页

‎2008学年度第一学期九年级数学期中试卷 ‎（测试时间：100分钟，满分：150分，范围：24.1-25.2）‎ 题号 一 二 ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ ‎25‎ 总分 得分 一、选择题（本大题共6题，每题4分，满分24分）‎ ‎1．如果点P是线段AB的黄金分割点，且AP>BP，那么AP的长为……（）.‎ ‎(A) AB； (B) AB； (C)AB； (D)AB.‎ ‎2．如果点D、E分别在ΔABC的边AB、AC上，下列条件中可以推出DE∥BC的是…（ ）‎ ‎ (A) = ，= ； （B） = ，= ；‎ ‎（C） = ，= ； (D) =，= ．‎ ‎3.下列命题中的真命题是………………………………………………（ ）‎ ‎ (A)两个直角三角形都相似; ‎ ‎(B)一个直角三角形的两条边和另一个直角三角形的两条边成比例，那么这两个直角三角形相似; ‎ ‎（C）两个等腰三角形都相似; ‎ ‎(D) 两个等腰直角三角形都相似.‎ ‎4.在△ABC中，点D、E分别在AB、AC 边上，∠B=∠AED，那么下列结论中不正确的是……………………………………………………… （ )‎ ‎（A）AD：AC=AE：AB； （B）AD·AB=AE·AC；‎ ‎（C）DE：BC=AD：AC； (D) DE：BC=AD：AB．‎ ‎5．在直角三角形中，一个锐角三角比的值 （ ）．‎ ‎(A)与这个三角形的面积的大小有关； (B)与这个角的邻边和对边有关；‎ ‎(C)只与这个角的大小有关； (D)只与这个三角形的斜边有关．‎ ‎6.如图，已知平行四边形ABCD，点M是边DC的中点，射线AM、BC相交于点E，设=，=，则向量关于、的分解式是（ ）‎ ‎（A）-2；（B）-2；（C）+2；（D）2+‎ ‎.‎ 二、填空题（本大题共12题，每题4分，满分48分）‎ ‎7．如果sinA=，那么锐角A=________度.‎ ‎8．若.‎ ‎9．已知线段厘米，厘米，那么线段和的比例中项＝厘米 ．‎ ‎10．计算： ．‎ ‎11．已知：，用向量、表示= .‎ ‎12.如图，AB//CD，AD与BC交于点O，若，则=．‎ ‎13.已知△ABC中,AC=6,AB=8,AD平分∠BAC,DE∥CA,则DE=.‎ ‎14.如图，在△ABC中,，四边形EDFC为内接正方形，AC=5，BC=3，则AE∶DF=.‎ ‎15．如果两个相似三角形的面积之比是4∶9，那么它们对应的角平分线之比是．‎ ‎16．如果直角三角形的斜边长为18，那么这个直角三角形的重心到直角顶点的距离为．‎ ‎17．如图，G为正方形ABCD的BC边上一点，CG=2，BG= 4，P为DC上一点，若PG⊥AG，则CP=．‎ ‎18．如果等腰三角形中的两条边长分别是4和5，那么底角的余弦为．‎ 三、解答题：（本大题共7题，19-22题，每题10分，23-24题，每题12分，25题14分，满分78分）‎ ‎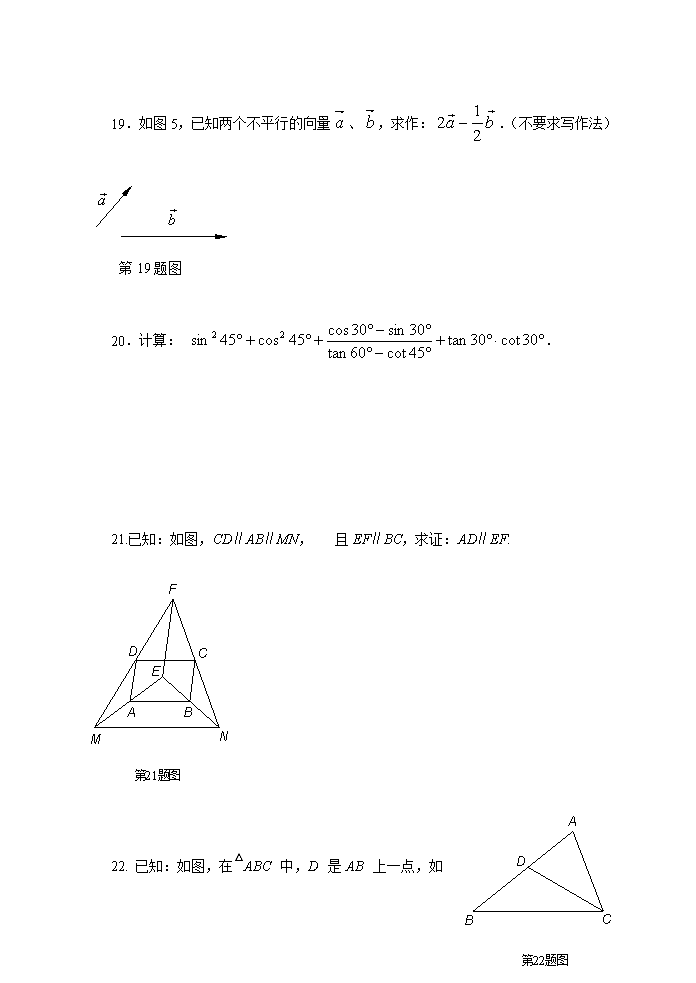19．如图5，已知两个不平行的向量、，求作：．（不要求写作法）‎ 第19题图 ‎20．计算： .‎ ‎21.已知：如图，CD∥AB∥MN， 且EF∥BC，求证：AD∥EF.‎ ‎22. 已知：如图，在△ABC中，D是AB上一点，如果∠B=∠ACD，AD=‎2cm，AC=‎4cm，S△ACD =‎8cm2，求△ABC的面积．‎ ‎23．在矩形ABCD中，AB=，AD=，P是BC的中点，AP和BD相交于点E，‎ 求证: AP⊥BD ‎24、如图，在□ABCD中，点E在BC边上，AE=AB，点F在DE上，∠DAF=∠CDE．‎ ‎（1）找出图中相似的三角形，有 ‎①∽；‎ ‎②∽.‎ 并证明②式.‎ ‎（2）如果AB=6，DF=5，求EF的长．‎ ‎25．如图，在梯形ABCD中，AB∥CD, CD=6，BC=4，∠ABD =∠C，P是CD上的一个动点(P不与点C点D重合),且满足条件:∠BPE =∠C, 交BD于点E.‎ ‎ (1 ) 求证：△BCP∽△PDE；‎ ‎（2）如果CP= x , BE=y，求y与x之间的函数关系式；‎ ‎（3）P点在运动过程中，△BPE能否成为等腰三角形，若能，求 x的值 ，若不能，说明理由.‎ 九年级数学期中试卷参考答案 一．1.A 2. C 3.D 4.D 5.C 6.B 二．7.60 8. 9. 4 10. 11. 12. 13. 14.5∶3 15. 2∶3 16. 6 17. 18.,‎ 三．19.略 ‎ ‎20.解：原式=+++×………………8分 ‎ =+++1=………………2分 ‎21.∵EF∥ BC∴…………………………………2分 ‎∵AB∥ MN∴………………………………2分 ‎∵CD∥ MN∴……………………………………2分 ‎∴…………………………………………………2分 ‎∴AD∥EF……………………………………………………2分 ‎22．∵在△ACD与△ABC中 ‎∠B=∠ACD ‎∠A=∠A ‎∴△ACD∽△ABC…………………………………………………3分 ‎∴………………………………………………………2分 ‎∵AD=‎2 cm，AC=‎‎4 cm ‎∴…………………………………………………2分 又∵S△ACD=‎8cm2∴S△ABC=‎32 cm2……………………………………3分 ‎23．∵矩形ABCD，∴AD=BC，∠DAB=∠ABP=90°…………………………2分 ‎∵AD=,P是BC的中点 ‎∴BP=………………………………1分 ‎∵AB=∴………………………………1分 ‎∵………………………………1分 ‎∴………………………………1分 ‎∵∠DAB=∠ABP=90°‎ ‎∴△DAB∽△ABP ………………………………1分 ‎∴∠ABD=∠BPA ………………………………1分 ‎∵∠ABD+∠EBP=90° ………………………………1分 ‎∴∠BPA+∠EBP=90° ………………………………1分 ‎∴∠BEP=90° ……………………………1分 ‎∴AP⊥BD ………………………………1分 ‎24．(1)①△DCE∽△AFD；②△AEF∽△DEA…………………………2分 证明②：∵∠AFE=∠FAD+∠ADF =∠EDC+∠ADF=∠ADC=∠B=∠AEB ‎=∠EAD，又∠AEF=∠DEA，∴△AEF∽△DEA ………………………4分 ‎(2) ∵AE=AB, AB=6， ∴AE=6……………………………1分 ‎∵△AEF∽△DEA ‎∴………………………………2分 设EF=x ，∵AB=6，DF=5‎ ‎∴，即 解得(不符合题意,舍去) ………………………………2分 EF的长为4.………………………………1分 ‎25．(1)证明:因为AB∥DC，所以∠ABD=∠BDC 因为∠ABD =∠C，所以∠BDC =∠C……………………………2分 因为∠BPD =∠BPE+∠EPD ‎∠BPD =∠PBC+∠C 又因为∠BPE =∠C 所以∠PBC =∠EPD……………………………………1分 所以△BCP∽△PDE…………………………………………1分 ‎(2) 因为△BCP∽△PDE 所以,……………………………………………………1分 因为CP= x , BE=y，BD=BC=4,CD=6‎ 所以DP= 6 - x , DE= 4 – y 所以,……………………………………………………2分 所以………………………………………………1分 ‎ (3)(ⅰ)若BP=PE，则△BCP≌△PDE，‎ 所以PD=BC=4,所以x=2 ……………………………………………2分 ‎(ⅱ)若BE=PE，则∠BPE=∠PBE=∠C=∠CDB，‎ 所以△BEP∽△CBD，PE：PB=BC：CD=2：3‎ 又因为PD：BC=PE：PB 即（6-x）：4=2：3，‎ 所以x=…………………………………………………………2分 ‎(ⅲ)若BP=BE，则∠BPE=∠PEB>∠CDB，矛盾.……………………1分 所以，当x=2或时，△BPE为等腰三角形.………………………1分