中考数学复习几何压轴题 19页

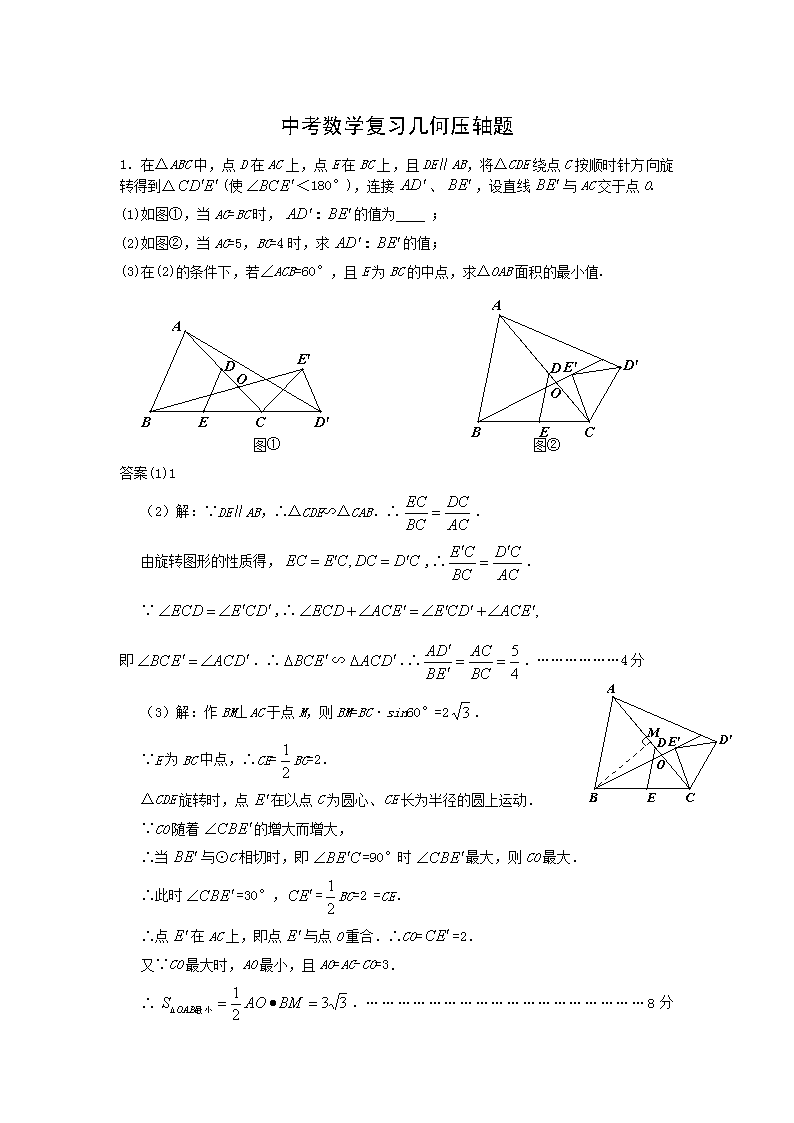
中考数学复习几何压轴题 ‎1．在△ABC中，点D在AC上，点E在BC上，且DE∥AB，将△CDE绕点C按顺时针方向旋转得到△(使＜180°)，连接、，设直线与AC交于点O.‎ ‎(1)如图①，当AC=BC时，:的值为 ；‎ ‎(2)如图②，当AC=5，BC=4时，求:的值； ‎ ‎(3)在(2)的条件下，若∠ACB=60°，且E为BC的中点，求△OAB面积的最小值.‎ ‎ ‎ 图① 图②‎ 答案(1)1‎ ‎（2）解：∵DE∥AB，∴△CDE∽△CAB．∴．‎ 由旋转图形的性质得，,∴．‎ ‎∵,∴‎ 即．∴∽.∴．………………4分 ‎（3）解：作BM⊥AC于点M，则BM=BC·sin60°=2．‎ ‎∵E为BC中点，∴CE=BC=2．‎ ‎△CDE旋转时，点在以点C为圆心、CE长为半径的圆上运动．‎ ‎∵CO随着的增大而增大，‎ ‎∴当与⊙C相切时，即=90°时最大，则CO最大．‎ ‎∴此时=30°，=BC=2 =CE．‎ ‎∴点在AC上，即点与点O重合．∴CO==2．‎ 又∵CO最大时，AO最小，且AO=AC-CO=3．‎ ‎∴．………………………………………………8分 ‎2．点A、B、C在同一直线上，在直线AC的同侧作和，连接AF，CE．取AF、CE的中点M、N，连接BM，BN， MN．‎ ‎(1)若和是等腰直角三角形，且(如图1)，则是 三角形．‎ ‎(2)在和中，若BA=BE,BC=BF,且，(如图2)，则是 三角形，且 .‎ ‎(3)若将(2)中的绕点B旋转一定角度,(如同3)，其他条件不变，那么(2)中的结论是否成立？ 若成立，给出你的证明；若不成立，写出正确的结论并给出证明.‎ 答案：（1）等腰直角 ………1分 ‎ （2）等腰 ………2分 ………3分 ‎ （3）结论仍然成立 ………4分 ‎ 证明： 在 ‎∴△ABF≌△EBC.‎ ‎∴AF=CE. ∠AFB=∠ECB.……5分 ‎∵M,N分别是AF、CE的中点,‎ ‎∴FM=CN.∴△MFB≌△NCB.‎ ‎∴BM=BN. ∠MBF=∠NBC.……6分 ‎∴∠MBN=∠MBF+∠FBN=∠FBN+∠NBC=∠FBC=.……7分 ‎3．图1是边长分别为4和3的两个等边三角形纸片和叠放在一起(与重合)．‎ ‎(1)固定△，将△绕点顺时针旋转得到△，连结(如图2)．此时线段与有怎样的数量关系？并证明你的结论；‎ ‎(2)设图2中的延长线交于，并将图2中的△在线段上沿着方向以每秒1个单位的速度平移，平移后的△设为△(如图3)．设△移动(点 在线段上)的时间为x秒，若△与△重叠部分的面积为y，求y与x之间的函数解析式，并写出自变量x的取值范围；‎ 图1 图2 图3 图4‎ ‎(3)若固定图1中的△，将△沿方向平移，使顶点C落在的中点处，再以点为中心顺时针旋转一定角度，设，边交于点M，边交于点N(如图4)．此时线段的值是否随的变化而变化？如果没有变化，请你求出的值；如果有变化，请你说明理由．‎ 答案：（1）. ………………………………………………………………1分 证明：如图2，∵△与△都是等边三角形，△绕点顺时针旋转30°得到△，‎ ‎∴△也是等边三角形，且，‎ ‎∴, . …………………………………2分 ‎∴,∴,∴.∴△≌△，‎ ‎∴ . ……………………………………3分 ‎（2）如图3，设分别与交于点.‎ ‎∵△CDE在线段CF上沿着CF方向以每秒1个单位的速度平移x秒，‎ 平移后的△为△，.‎ 由（1）可知，，‎ ‎..‎ ‎,.在中，，..…………………4分 过点作于点.‎ 在中， ，‎ ‎.. ‎ ‎，.‎ 当点与点重合时，，∵，∴.‎ ‎∴此函数自变量x的取值范围是 . …………………………………………6分 ‎（3）的值不变 . ……………………………………………………7分 证明：如图4，由题意知，，∴，‎ 在中，，∴.‎ 又∵，∴△∽△，∴．‎ ‎∵点是的中点，，∴，‎ ‎∴，∴． …………………………………………………8分 ‎4． 以的两边AB、AC为腰分别向外作等腰Rt和等腰Rt，连接DE，M、N分别是BC、DE的中点．探究：AM与DE的位置及数量关系．‎ ‎(1)如图① 当为直角三角形时，AM与DE的位置关系是 ，线段AM与DE的数量关系是 ；‎ ‎(2)将图①中的等腰Rt绕点A沿逆时针方向旋转(0<<90)后，如图②所示，(1)问中得到的两个结论是否发生改变？并说明理由．‎ 答案：（1）， ‎ ‎ 　　（2）结论仍然成立。‎ 证明：如图，延长CA至F，使FA=AC，FA交DE于点P，并连结． ‎ ‎，．‎ 在与中：‎ ‎(SAS) .‎ BF=DE, .‎ · ‎.‎ ‎ .又CA=AF, CM=MB，‎ · AM // FB 且AM=FB，‎ ‎, AM=DE． ‎ ‎5． (1)如图1，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是边BC、CD上的点，且∠EAF=∠BAD.求证:EF＝BE＋FD;‎ ‎ (2) 如图2在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD上的点，且∠EAF=∠BAD, (1)中的结论是否仍然成立？不用证明. ‎ ‎(3) 如图25-3在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E、F分别是边BC、CD延长线上的点，且∠EAF=∠BAD, (1)中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明.‎ 答案：（1）证明：延长EB到G，使BG=DF，联结AG. ‎ ‎∵∠ABG＝∠ABC=∠D＝90°, AB＝AD，∴△ABG≌△ADF.‎ ‎∴AG＝AF, ∠1＝∠2． --------------------1分 ‎∴∠1+∠3＝∠2+∠3=∠EAF=∠BAD．‎ ‎∴∠GAE=∠EAF．又AE＝AE，∴△AEG≌△AEF.‎ ‎∴EG＝EF． -----------------2分 ‎∵EG=BE+BG．∴EF= BE＋FD --------3分 ‎(2) (1)中的结论EF= BE＋FD仍然成立. ---------------------------4分 ‎（3）结论EF=BE＋FD不成立，应当是EF=BE-FD．--------------------5分 证明：在BE上截取BG，使BG=DF，连接AG．‎ ‎∵∠B+∠ADC＝180°,∠ADF+∠ADC＝180°，∴∠B＝∠ADF．‎ ‎∵AB＝AD，∴△ABG≌△ADF.∴∠BAG＝∠DAF,AG＝AF． ‎ ‎∴∠BAG+∠EAD＝∠DAF+∠EAD=∠EAF =∠BAD．‎ ‎∴∠GAE=∠EAF．‎ ‎∵AE＝AE，∴△AEG≌△AEF.∴EG＝EF ---------------------6分 ‎∵EG=BE-BG，∴EF=BE-FD． ---------------------7分 ‎6． (1)如图1，四边形中，，，，请你猜想线段、之和与线段的数量关系，并证明你的结论；‎ ‎(2)如图2，四边形中，，，若点为四边形内一点，且，请你猜想线段、、之和与线段的数量关系，并证明你的结论．‎ 图2‎ 图１‎ ‎　　　‎ 答案：（1）如图１，延长至，使．‎ 可证明是等边三角形． ……………………………………………1分 联结，可证明≌． ……………………………………………2分 图1‎ 图2‎ 故．……………………………………………3分 ‎（2）如图２，在四边形外侧作正三角形，‎ ‎ 可证明≌，得．…………………………………………4分 ‎∵ 四边形符合（1）中条件，∴ ．………………………5分 联结，‎ ⅰ）若满足题中条件的点在上，则．∴ ．‎ ‎∴ ． ……………………………………………6分 ⅱ）若满足题中条件的点不在上，‎ ‎∵ ，∴ ．‎ ‎∴ ． ……………………………………………7分 综上，． ……………………………………………8分 如图10，在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2=17,且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根. （1）求C点的坐标； （2）以斜边AB为直径作圆与y轴交于另一点E，求过A、B、E三点的抛物线的解析式，并画出此抛物线的草图； （3）在抛物线上是否存在点P，使△ABP与△ABC全等？若存在，求出符合条件的P点的坐标；若不存在，说明理由.‎ 解：（1）∵线段OA、OB的长度是关于x的一元二次方程x2－mx+2(m－3)=0的两个根，‎ A O 图10‎ E B G x C y E′‎ ‎∴　　又　∵OA2+OB2=17，‎ ‎∴（OA+OB）2－2·OA·OB=17.（3）‎ ‎∴把（1）（2）代入（3），得m2－4(m－3)=17.‎ ‎∴m2－4m－5=0.，　　解得m=-1或m=5.‎ 又知OA+OB=m>0，∴m=－1应舍去.‎ ‎∴当m=5时，得方程x2－5x+4=0.解之，得x=1或x=4.‎ ‎∵BC>AC,　　∴OB>OA. ∴OA=1，OB=4.‎ 在Rt△ABC中，∠ACB=90°，CO⊥AB，‎ ‎∴OC2=OA·OB=1×4=4. ∴OC=2，　∴　C（0，2）.‎ ‎（2）∵OA=1，OB=4，C、E两点关于x轴对称，‎ ‎∴A(－1,0),B(4,0),E(0,－2).‎ 设经过A、B、E三点的抛物线的解析式为y=ax2+bx+c,则 ‎ ‎ ‎ ∴所求抛物线解析式为 ‎（3）存在.∵点E是抛物线与圆的交点，‎ ‎∴Rt△ACB≌△AEB. ‎ ‎ ∴E（0，-2）符合条件.‎ ‎∵圆心的坐标（，0）在抛物线的对称轴上，‎ ‎∴这个圆和这条抛物线均关于抛物线的对称轴对称.‎ ‎∴点E关于抛物线对称轴的对称点E′也符合题意. ‎ ‎ ∴可求得E′（3，-2）.‎ ‎∴抛物线上存在点P符合题意，它们的坐标是（0，-2）和（3，-2）。‎ 如图8，PA切⊙O于点A，PBC交⊙O于点B、C，若PB、PC的长是关于x的方程的两根，且BC=4，求:（1）m的值；（2）PA的长；‎ A B C P ‎·‎ O 图8‎ 解：由题意知：（1）PB+PC=8，BC=PC－PB=2 ‎ ‎∴PB=2，PC=6‎ ‎∴PB·PC=(m+2)=12‎ ‎∴m=10 ‎ ‎（2）∴PA2=PB·PC=12‎ ‎∴PA= ‎ ‎23.已知双曲线和直线相交于点A（，）和点B（，），且,求的值.‎ 解：由,得 ‎ ∴＝－，＝－ ‎ ‎ 故＝（）2－2＝＝10‎ ‎ ∴　∴或，‎ ‎ 又△即，舍去，故所求值为1. ‎ ‎24．（10分）一艘渔船在A处观测到东北方向有一小岛C，已知小岛C周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处，在B处测得小岛C在北偏东60°方向，这时渔船改变航线向正东(即BD)方向航行，这艘渔船是否有进入养殖场的危险？‎ 解法一：过点B作BM⊥AH于M，∴BM∥AF.∴∠ABM=∠BAF=30°.‎ ‎　 在△BAM中，AM=AB=5，BM=.　 ‎ ‎　　　　过点C作CN⊥AH于N，交BD于K.‎ ‎　　　　在Rt△BCK中，∠CBK=90°-60°=30°‎ ‎　　　 设CK=，则BK=　　 ‎ ‎　　　　在Rt△ACN中，∵∠CAN=90°-45°=45°，‎ ‎　　　　∴AN=NC.∴AM+MN=CK+KN.‎ ‎　　　　又NM=BK，BM=KN.‎ ‎　　　　∴.解得 ‎　　　 ∵5海里＞4.8海里，‎ ‎∴渔船没有进入养殖场的危险.　　 ‎ ‎　　　　答：这艘渔船没有进入养殖场危险.　　 ‎ ‎　　解法二：过点C作CE⊥BD，垂足为E，∴CE∥GB∥FA.‎ ‎　　　　∴∠BCE=∠GBC=60°.∠ACE=∠FAC=45°.‎ ‎　　　　∴∠BCA=∠BCE-∠ACE=60°-45°=15°.‎ ‎　　　　又∠BAC=∠FAC-∠FAB=45°-30°=15°，‎ ‎∴∠BCA=∠BAC.∴BC=AB=10.‎ ‎　　　　在Rt△BCE中，CE=BC·cos∠BCE=BC·cos60°=10×=5(海里).‎ ‎　　　　∵5海里＞4.8海里，‎ ‎∴渔船没有进入养殖场的危险.‎ ‎　　　答：这艘渔船没有进入养殖场的危险.‎ ‎25. （10分）如图，某隧道口的横截面是抛物线形，已知路宽AB为6米，最高点离地面的距离OC为5米．以最高点O为坐标原点，抛物线的对称轴为y轴，1米为数轴的单位长度，建立平面直角坐标系，求:（1）以这一部分抛物线为图象的函数解析式，并写出x的取值范围；（2）有一辆宽2.8米，高1米的农用货车（货物最高处与地面AB的距离）能否通过此隧道？‎ 解：（1）设所求函数的解析式为． ‎ 由题意，得 函数图象经过点B（3，-5）， ‎ ‎∴-5=9a． ‎ ‎∴． ‎ ‎∴所求的二次函数的解析式为． ‎ x的取值范围是． ‎ ‎（2）当车宽米时，此时CN为米，对应，‎ EN长为，车高米，∵，‎ ‎∴农用货车能够通过此隧道。‎ ‎26. （10分）已知：如图，⊙O和⊙O相交于A、B两点， 动点P在⊙O上，且在⊙ 外，直线PA、PB分别交⊙O于C、D.问：⊙O的弦CD的长是否随点P的运动而发生变化？如果发生变化，请你确定CD最长和最短时P的位置，如果不发生变化，请你给出证明； ‎ 解：当点P运动时，CD的长保持不变，A、B是⊙O与⊙O的交点，弦AB与点P的位置关系无关，连结AD，∠ADP在⊙O中所对的弦为AB，所以∠ADP为定值，∠P在⊙O中所对的弦为AB，所以∠P为定值.‎ ‎∵∠CAD =∠ADP +∠P，∴∠CAD为定值，‎ 在⊙O中∠CAD对弦CD，‎ ‎∴CD的长与点P的位置无关.毛 ‎27、已知x1、x2是关于x的方程x2-6x+k=0的两个实数根，且x12x22-x1-x2=115，‎ ‎（1）求k的值； （2）求x12+x22+8的值. ‎ ‎（1）k=-11；（2）66‎ 五、（24小题10分，25小题11分，共21分）‎ ‎28、如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连结DE. ‎ (1) DE与半圆O相切吗？若相切，请给出证明；若不相切，请说明理由；‎ (2) 若AD、AB的长是方程x2－10x+24=0的两个根，求直角边BC的长。‎ ‎29．已知：如图9，等腰梯形ABCD的边BC在x轴上，点A在y轴的正方向上，A( 0, 6 )，D ( 4，6），且AB＝.‎ ‎（1）求点B的坐标；‎ ‎（2）求经过A、B、D三点的抛物线的解析式；‎ ‎（3）在（2）中所求的抛物线上是否存在一点P，使得S△ABC = S梯形ABCD ?若存在，请求出该点坐标，若不存在，请说明理由.‎ ‎28、解：（1）DE与半圆O相切. ‎ ‎ 证明： 连结OD、BD ∵AB是半圆O的直径 ‎ ∴∠BDA=∠BDC=90° ∵在Rt△BDC中,E是BC边上的中点 ‎∴DE=BE∴∠EBD＝∠BDE ‎ ‎∵OB=OD∴∠OBD=∠ODB ‎ 又∵∠ABC＝∠OBD+∠EBD＝90° ‎ ‎∴∠ODB+∠EBD=90°∴DE与半圆O相切. ‎ ‎ （2）解：∵在Rt△ABC中，BD⊥AC ‎ ‎ ∴ Rt△ABD∽Rt△ABC ‎ ‎ ∴ = 即AB2=AD·AC∴ AC= ‎ ‎ ∵ AD、AB的长是方程x2－10x+24=0的两个根 ‎ ‎ ∴ 解方程x2－10x+24=0得： x1=4 x2=6 ‎ ‎ ∵ AD