中考数学压轴题100题精选及答案 150页

中考数学压轴题100题精选 ‎【001】如图，已知抛物线（a≠0）经过点，抛物线的顶点为，过作射线．过顶点平行于轴的直线交射线于点，在轴正半轴上，连结． ‎ ‎（1）求该抛物线的解析式；‎ ‎（2）若动点从点出发，以每秒1个长度单位的速度沿射线运动，设点运动的时间为．问当为何值时，四边形分别为平行四边形？直角梯形？等腰梯形？‎ ‎（3）若，动点和动点分别从点和点同时出发，分别以每秒1个长度单位和2个长度单位的速度沿和运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为，连接，当为何值时，四边形的面积最小？并求出最小值及此时的长．‎ x y M C D P Q O A B A C B P Q E D 图16‎ ‎【002】如图16，在Rt△ABC中，∠C=90°，AC = 3，AB = 5．点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动．伴随着P、Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线QB-BC-CP于点E．点P、Q同时出发，当点Q到达点B时停止运动，点P也随之停止．设点P、Q运动的时间是t秒（t＞0）．‎ ‎（1）当t = 2时，AP = ，点Q到AC的距离是 ；‎ ‎（2）在点P从C向A运动的过程中，求△APQ的面积S与 t的函数关系式；（不必写出t的取值范围）‎ ‎（3）在点E从B向C运动的过程中，四边形QBED能否成 为直角梯形？若能，求t的值．若不能，请说明理由；‎ ‎（4）当DE经过点C 时，请直接写出t的值． ‎ ‎【003】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（4，0）、C（8，0）、D（8，8）.抛物线y=ax2+bx过A、C两点. ‎ ‎(1)直接写出点A的坐标，并求出抛物线的解析式；‎ ‎ (2)动点P从点A出发．沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD 向终点D运动．速度均为每秒1个单位长度，运动时间为t秒.过点P作PE⊥AB交AC于点E，①过点E作EF⊥AD于点F，交抛物线于点G.当t为何值时，线段EG最长?‎ ‎②连接EQ．在点P、Q运动的过程中，判断有几个时刻使得△CEQ是等腰三角形?‎ 请直接写出相应的t值。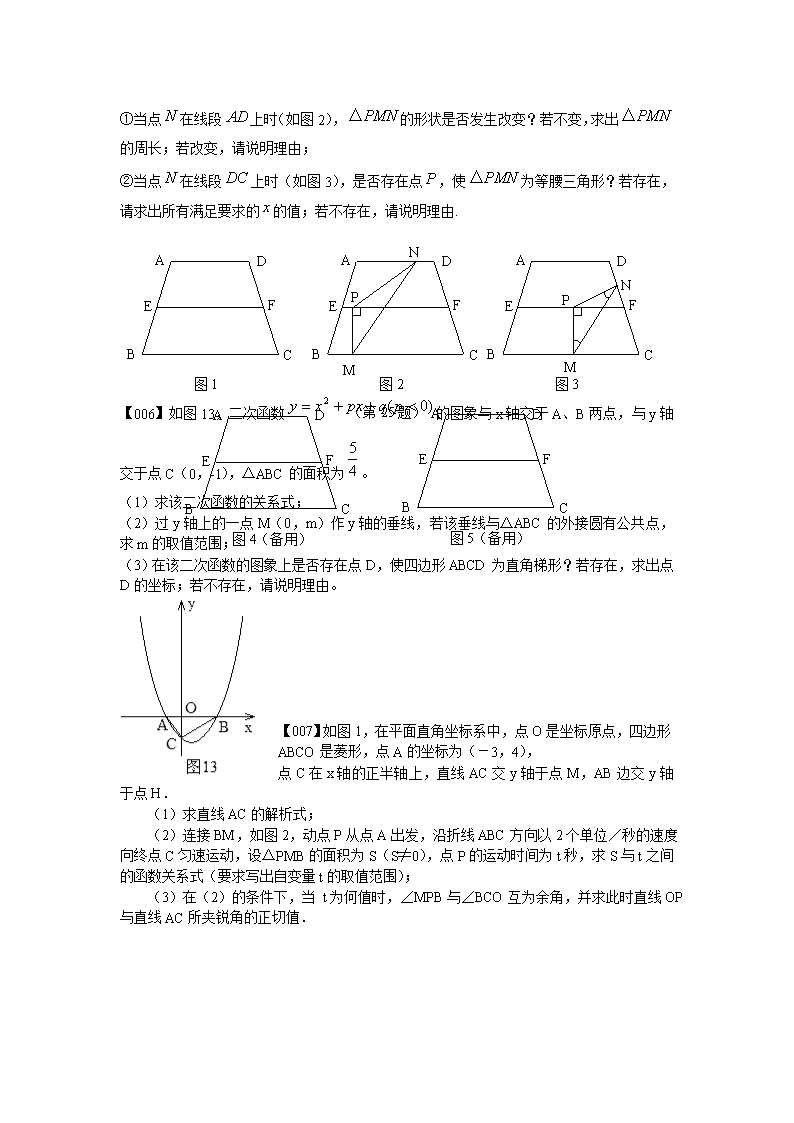‎ ‎【004】如图，已知直线与直线相交于点分别交轴于两点．矩形的顶点分别在直线上，顶点都在轴上，且点与点重合．‎ ‎ （1）求的面积；‎ ‎（2）求矩形的边与的长；‎ ‎（3）若矩形从原点出发，沿轴的反方向以每秒1个单位长度的速度平移，‎ 设移动时间为秒，矩形与重叠部分的面积为，求关 A D B E O C F x y y ‎（G）‎ 的函数关系式，并写出相应的的取值范围．‎ ‎【005】如图1，在等腰梯形中，，是的中点，过点作交于点．，.‎ ‎（1）求点到的距离；‎ ‎（2）点为线段上的一个动点，过作交于点，过作交折线于点，连结，设.‎ ‎①当点在线段上时（如图2），的形状是否发生改变？若不变，求出的周长；若改变，请说明理由；‎ ‎②当点在线段上时（如图3），是否存在点，使为等腰三角形？若存在，请求出所有满足要求的的值；若不存在，请说明理由.‎ A D E B F C 图4（备用）‎ A D E B F C 图5（备用）‎ A D E B F C 图1‎ 图2‎ A D E B F C P N M 图3‎ A D E B F C P N M ‎（第25题）‎ ‎【006】如图13，二次函数的图象与x轴交于A、B两点，与y轴交于点C（0，-1），ΔABC的面积为。‎ ‎（1）求该二次函数的关系式；‎ ‎（2）过y轴上的一点M（0，m）作y轴的垂线，若该垂线与ΔABC的外接圆有公共点，求m的取值范围；‎ ‎（3）在该二次函数的图象上是否存在点D，使四边形ABCD为直角梯形？若存在，求出点D的坐标；若不存在，请说明理由。‎ ‎【007】如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（－3，4），‎ 点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H．‎ ‎ （1）求直线AC的解析式；‎ ‎ （2）连接BM，如图2，动点P从点A出发，沿折线ABC方向以2个单位／秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（要求写出自变量t的取值范围）；‎ ‎ （3）在（2）的条件下，当 t为何值时，∠MPB与∠BCO互为余角，并求此时直线OP与直线AC所夹锐角的正切值．‎ ‎ ‎ ‎【008】如图所示，在直角梯形ABCD中，∠ABC=90°，AD∥BC，AB=BC，E是AB的中点，CE⊥BD。‎ 求证：BE=AD；‎ 求证：AC是线段ED的垂直平分线；‎ ‎△DBC是等腰三角形吗？并说明理由。‎ ‎【009】一次函数的图象分别与轴、轴交于点，与反比例函数的图象相交于点．过点分别作轴，轴，垂足分别为；过点 分别作轴，轴，垂足分别为与交于点，连接．‎ ‎（1）若点在反比例函数的图象的同一分支上，如图1，试证明：‎ ‎①；‎ ‎②．‎ O C F M D E N K y x O C D K F E N y x M ‎（2）若点分别在反比例函数的图象的不同分支上，如图2，则与还相等吗？试证明你的结论．‎ ‎【010】如图，抛物线与轴交于两点，与轴交于C点，且经过点，对称轴是直线，顶点是．‎ ‎（1）求抛物线对应的函数表达式；‎ ‎（2）经过两点作直线与轴交于点，在抛物线上是否存在这样的点，使以点为顶点的四边形为平行四边形？若存在，请求出点的坐标；若不存在，请说明理由；‎ ‎（3）设直线与y轴的交点是，在线段上任取一点（不与重合），经过三点的圆交直线于点，试判断的形状，并说明理由；‎ ‎（4）当是直线上任意一点时，（3）中的结论是否成立？（请直接写出结论）．‎ O B x y A M C ‎1‎ ‎【011】已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．‎ ‎（1）求证：EG=CG；‎ ‎（2）将图①中△BEF绕B点逆时针旋转45º，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由． ‎ ‎（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）‎ D F B A C E 第24题图③‎ F B A D C E G 第24题图②‎ F B A D C E G 第24题图①‎ ‎ ‎ ‎【012】如图，在平面直角坐标系中，半径为1的圆的圆心在坐标原点，且与两坐标轴分别交于四点．抛物线与轴交于点，与直线交于点，且分别与圆相切于点和点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）抛物线的对称轴交轴于点，连结，并延长交圆于，求的长．‎ ‎（3）过点作圆的切线交的延长线于点，判断点是否在抛物线上，说明理由．‎ O x y N C D E F B M A ‎【013】如图，抛物线经过三点．‎ ‎（1）求出抛物线的解析式；‎ ‎（2）P是抛物线上一动点，过P作轴，垂足为M，是否存在P点，使得以A，P，M为顶点的三角形与相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；‎ ‎（3）在直线AC上方的抛物线上有一点D，使得的面积最大，求出点D的坐标．‎ O x y A B C ‎4‎ ‎1‎ ‎（第26题图）‎ ‎【014】在平面直角坐标中，边长为2的正方形的两顶点、分别在轴、轴的正半轴上，点在原点.现将正方形绕点顺时针旋转，当点第一次落在直线上时停止旋转，旋转过程中，边交直线于点，边交轴于点（如图）.‎ ‎（1）求边在旋转过程中所扫过的面积；‎ ‎(第26题)‎ O A B C M N ‎（2）旋转过程中，当和平行时，求正方形 ‎ 旋转的度数；‎ ‎（3）设的周长为，在旋转正方形 的过程中，值是否有变化？请证明你的结论.‎ ‎【015】如图，二次函数的图象经过点D(0，)，且顶点C的横坐标为4，该图象在x 轴上截得的线段AB的长为6.‎ ‎⑴求二次函数的解析式；‎ ‎⑵在该抛物线的对称轴上找一点P，使PA+PD最小，求出点P的坐标；‎ ‎⑶在抛物线上是否存在点Q，使△QAB与△ABC相似？如果存在，求出点Q的坐标；如果不存在，请说明理由．‎ ‎【016】如图9，已知正比例函数和反比例函数的图象都经过点．‎ ‎（1）求正比例函数和反比例函数的解析式；‎ ‎（2）把直线OA向下平移后与反比例函数的图象交于点，求的值和这个一次函数的解析式；‎ ‎（3）第（2）问中的一次函数的图象与轴、轴分别交于C、D，求过A、B、D三点的二次函数的解析式；‎ y x O C D B A ‎3‎ ‎3‎ ‎6‎ ‎（4）在第（3）问的条件下，二次函数的图象上是否存在点E，使四边形OECD的面积与四边形OABD的面积S满足：？若存在，求点E的坐标；‎ 若不存在，请说明理由．‎ ‎【017】如图，已知抛物线经过，两点，顶点为．‎ ‎（1）求抛物线的解析式；‎ ‎（2）将绕点顺时针旋转90°后，点落到点的位置，将抛物线沿轴平移后经过点，求平移后所得图象的函数关系式；‎ ‎（3）设（2）中平移后，所得抛物线与轴的交点为，顶点为，若点在平移后的抛物线上，且满足的面积是面积的2倍，求点的坐标．‎ y x B A O D ‎（第26题）‎ ‎【018】如图，抛物线经过、两点，与轴交于另一点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）已知点在第一象限的抛物线上，求点关于直线对称的点的坐标；‎ ‎（3）在（2）的条件下，连接，点为抛物线上一点，且，求点的坐标．‎ y x O A B C ‎【019】如图所示，将矩形OABC沿AE折叠，使点O恰好落在BC上F处，以CF为边作正方形CFGH，延长BC至M，使CM＝｜CF—EO｜，再以CM、CO为边作矩形CMNO ‎(1)试比较EO、EC的大小，并说明理由 ‎(2)令，请问m是否为定值？若是，请求出m的值；若不是，请说明理由 ‎(3)在(2)的条件下，若CO＝1，CE＝，Q为AE上一点且QF＝，抛物线y＝mx2+bx+c经过C、Q两点，请求出此抛物线的解析式.‎ ‎ (4)在(3)的条件下，若抛物线y＝mx2+bx+c与线段AB交于点P，试问在直线BC上是否存在点K，使得以P、B、K为顶点的三角形与△‎ AEF相似?若存在，请求直线KP与y轴的交点T的坐标?若不存在，请说明理由。‎ ‎【020】如图甲，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连结AD，以AD为一边且在AD的右侧作正方形ADEF。‎ 解答下列问题：‎ ‎（1）如果AB=AC，∠BAC=90°，①当点D在线段BC上时（与点B不重合），如图乙，线段CF、BD之间的位置关系为 ，数量关系为 。‎ ‎②当点D在线段BC的延长线上时，如图丙，①中的结论是否仍然成立，为什么？‎ ‎（2）如果AB≠AC，∠BAC≠90°点D在线段BC上运动。‎ 试探究：当△ABC满足一个什么条件时，CF⊥BC（点C、F重合除外）？画出相应图形，并说明理由。（画图不写作法）‎ ‎（3）若AC=4，BC=3，在（2）的条件下，设正方形ADEF的边DE与线段CF相交于点P，求线段CP长的最大值。‎ ‎【021】如图，点P是双曲线上一动点，过点P作x轴、y轴的垂线，分别交x轴、y轴于A、B两点，交双曲线y= （0＜k2＜|k1|）于E、F两点．‎ ‎（1）图1中，四边形PEOF的面积S1= ▲ (用含k1、k2的式子表示)；‎ ‎（2）图2中，设P点坐标为（－4，3）．‎ ‎①判断EF与AB的位置关系，并证明你的结论；‎ ‎②记，S2是否有最小值？若有，求出其最小值；若没有，请说明理由。‎ ‎【022】一开口向上的抛物线与x轴交于A(m－2，0)，B(m＋2，0)两点，记抛物线顶点为C，且AC⊥BC．‎ ‎(1)若m为常数，求抛物线的解析式；‎ ‎(2)若m为小于0的常数，那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点？‎ ‎(3)设抛物线交y轴正半轴于D点，问是否存在实数m，使得△BCD为等腰三角形？若存在，求出m的值；若不存在，请说明理由．‎ ‎【023】如图，在梯形中，点是的中点，是等边三角形．‎ ‎（1）求证：梯形是等腰梯形；‎ ‎（2）动点、分别在线段和上运动，且保持不变．设求与的函数关系式；‎ ‎（3）在（2）中：①当动点、运动到何处时，以点、和点、、、中的两个点为顶点的四边形是平行四边形？并指出符合条件的平行四边形的个数；②当取最小值时，判断的形状，并说明理由．‎ A D C B P M Q ‎60°‎ ‎【024】如图，已知为直角三角形，，,点、在轴上，点坐标为（，）（），线段与轴相交于点，以（1，0）为顶点的抛物线过点、．‎ ‎（1）求点的坐标（用表示）；‎ ‎（2）求抛物线的解析式；‎ ‎ ‎ ‎ ‎ ‎（3）设点为抛物线上点至点之间的一动点，连结并延长交于点，连结 并延长交于点，试证明：为定值．‎ ‎【025】如图12，直线与两坐标轴分别相交于A、B点，点M是线段AB上任意一点（A、B两点除外），过M分别作MC⊥OA于点C，MD⊥OB于D．‎ ‎（1）当点M在AB上运动时，你认为四边形OCMD的周长是否发生变化？并说明理由；‎ ‎（2）当点M运动到什么位置时，四边形OCMD的面积有最大值？最大值是多少？‎ ‎（3）当四边形OCMD为正方形时，将四边形OCMD沿着x轴的正方向移动，设平移的距离为，正方形OCMD与△AOB重叠部分的面积为S．试求S与的函数关系式并画出该函数的图象．‎ B x y M C D O A 图12（1）‎ B x y O A 图12（2）‎ B x y O A 图12（3）‎ ‎【026】如图11，在△ABC中，∠C=90°，BC=8，AC=6，另有一直角梯形DEFH ‎（HF∥DE，∠HDE=90°）的底边DE落在CB上，腰DH落在CA上，且DE=4，∠DEF=∠CBA，AH∶AC=2∶3‎ ‎（1）延长HF交AB于G，求△AHG的面积. ‎（2）操作：固定△ABC，将直角梯形DEFH以每秒1个 单位的速度沿CB方向向右移动，直到点D与点B 重合时停止，设运动的时间为t秒，运动后的直角梯 形为DEFH′（如图12）. 探究1：在运动中，四边形CDH′H能否为正方形？若能， ‎ 请求出此时t的值；若不能，请说明理由. 探究2：在运动过程中，△ABC与直角梯形DEFH′重叠 部分的面积为y，求y与t的函数关系. ‎【027】阅读材料：‎ ‎ 如图12-1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法：，即三角形面积等于水平宽与铅垂高乘积的一半.‎ ‎ 解答下列问题：‎ ‎ 如图12-2，抛物线顶点坐标为点C(1,4),交x轴于点A(3,0)，交y轴于点B.‎ ‎(1)求抛物线和直线AB的解析式；‎ ‎(2)点P是抛物线(在第一象限内)上的一个动点，连结PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及；‎ 图12-2‎ x C O y A B D ‎1‎ ‎1‎ ‎(3)是否存在一点P，使S△PAB=S△CAB，若存在,求出P点的坐标；若不存在，请说明理由.‎ ‎【028】如图，已知抛物线与交于A(－1，0)、E(3，0)两点，与轴交于点B(0，3)。‎ 求抛物线的解析式；‎ 设抛物线顶点为D，求四边形AEDB的面积；‎ ‎△AOB与△DBE是否相似？如果相似，请给以证明；如果不相似，请说明理由。‎ ‎【029】已知二次函数。‎ ‎（1）求证：不论a为何实数，此函数图象与x轴总有两个交点。‎ ‎（2）设a<0，当此函数图象与x轴的两个交点的距离为时，求出此二次函数的解析式。‎ ‎（3）若此二次函数图象与x轴交于A、B两点，在函数图象上是否存在点P，使得△PAB的面积为，若存在求出P点坐标，若不存在请说明理由。‎ ‎【030】如图，已知射线DE与轴和轴分别交于点和点．动点从点出发，以1个单位长度/秒的速度沿轴向左作匀速运动，与此同时，动点P从点D出发，也以1个单位长度/秒的速度沿射线DE的方向作匀速运动．设运动时间为秒．‎ ‎（1）请用含的代数式分别表示出点C与点P的坐标；‎ O x y E P D A B M C ‎（2）以点C为圆心、个单位长度为半径的与轴交于A、B两点（点A在点B的左侧），连接PA、PB．‎ ‎①当与射线DE有公共点时，求的取值范围；‎ ‎②当为等腰三角形时，求的值．‎ ‎【031】已知直角坐标系中菱形ABCD的位置如图，C，D两点的坐标分别为(4,0)，(0,3).‎ 现有两动点P,Q分别从A,C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA 向终点A运动，设运动时间为t秒.‎ ‎（1）填空：菱形ABCD的边长是 ▲ 、面积是 ▲ 、 高BE的长是 ▲ ；‎ ‎（2）探究下列问题：‎ ‎①若点P的速度为每秒1个单位，点Q的速度为每秒2个单位.当点Q在线段BA上时，求 ‎△APQ的面积S关于t的函数关系式，以及S的最大值； ‎ ‎②若点P的速度为每秒1个单位，点Q的速度变为每秒k个单位，在运动过程中,任何时刻都有相应的k值，使得△APQ沿它的一边翻折，翻折前后两个三角形组成的四边形为菱形.请探究当t=4秒时的情形，并求出k的值。‎ ‎【032】如图，已知A、B是线段MN上的两点，，，．以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，使M、N两点重合成一点C，构成△ABC，设．‎ C A B N M ‎（1）求x的取值范围；‎ ‎（2）若△ABC为直角三角形，求x的值；‎ ‎（3）探究：△ABC的最大面积？‎ ‎【033】已知抛物线（）与轴相交于点，顶点为.直线分别与轴，轴相交于两点，并且与直线相交于点.‎ ‎(1)填空：试用含的代数式分别表示点与的坐标，则； ‎ ‎(2)如图，将沿轴翻折，若点的对应点′恰好落在抛物线上，′与轴交于点，连结，求的值和四边形的面积；‎ ‎(3)在抛物线（）上是否存在一点，使得以为顶点的四边形是平行四边形？若存在，求出点的坐标；若不存在，试说明理由.‎ 第（2）题 x y B C O D A M N N′‎ x y B C O A M N 备用图 ‎【034】若P为所在平面上一点，且，则点叫做的费马点.‎ ‎（1）若点为锐角的费马点，且，则的值为________；‎ ‎（2）如图，在锐角外侧作等边′连结′.‎ 求证：′过的费马点，且′=.‎ A C B ‎035】如图①，正方形 ABCD中，点A、B的坐标分别为（0，10），（8，4）， ‎ 点C在第一象限．动点P在正方形 ABCD的边上，从点A出发沿A→B→C→D匀速运动， ‎ 同时动点Q以相同速度在x轴正半轴上运动，当P点到达D点时，两点同时停止运动， ‎ 设运动的时间为t秒．‎ ‎(1)当P点在边AB上运动时，点Q的横坐标（长度单位）关于运动时间t（秒）的函数图象如图②所示，请写出点Q开始运动时的坐标及点P运动速度；‎ ‎(2)求正方形边长及顶点C的坐标；‎ ‎(3)在（1）中当t为何值时，△OPQ的面积最大，并求此时P点的坐标；‎ ‎(4)如果点P、Q保持原速度不变，当点P沿A→B→C→D匀速运动时，OP与PQ能否相 等，若能，写出所有符合条件的t的值；若不能，请说明理由．‎ ‎【036】已知：如图，在平面直角坐标系中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=2，OC=3．过原点O作∠AOC的平分线交AB于点D，连接DC，过点D作DE⊥DC，交OA于点E．‎ ‎（1）求过点E、D、C的抛物线的解析式；‎ ‎（2）将∠EDC绕点D按顺时针方向旋转后，角的一边与y轴的正半轴交于点F，另一边与线段OC交于点G．如果DF与（1）中的抛物线交于另一点M，点M的横坐标为，那么EF=2GO是否成立？若成立，请给予证明；若不成立，请说明理由；‎ ‎（3）对于（2）中的点G，在位于第一象限内的该抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．‎ y x D B C A E E O ‎【037】已知平行于x轴的直线与函数和函数的图像分别交于点A和点B，又有定点P（2，0） .[来源:Zxxk.Com]‎ ‎（1）若，且tan∠POB=，求线段AB的长；‎ ‎（2）在过A，B两点且顶点在直线上的抛物线中，已知线段AB=，且在它的对称轴左边时，y随着x的增大而增大，试求出满足条件的抛物线的解析式；‎ ‎（3）已知经过A，B，P三点的抛物线，平移后能得到的图像，求点P到直线AB的距离。‎ ‎【038】如图1，在平面直角坐标系中，O为坐标原点，点A的坐标为（－8，0），直线BC经过点B（－8，6），将四边形OABC绕点O按顺时针方向旋转α度得到四边形OA′B′C′，此时声母OA′、直线B′C′分别与直线BC相交于P、Q．‎ ‎（1）四边形的形状是 ，‎ 当α=90°时，的值是 ．‎ ‎（2）①如图2,当四边形OA′B′C′的顶点B′落在y轴正半轴上时,求的值;‎ ‎②如图3,当四边形OA′B′C′的顶点B′落在直线BC上时,求ΔOPB′的面积．‎ ‎（3）在四边形OABC旋转过程中,当时，是否存在这样的点P和点Q，使BP=？若存在，请直接写出点P的坐标；基不存在，请说明理由．‎ ‎【039】如图，已知点A(-4，8)和点B(2，n)在抛物线上．‎ ‎　　(1)　求a的值及点B关于x轴对称点P的坐标，并在x轴上找一点Q，使得AQ+QB最短，求出点Q的坐标；‎ ‎　　(2)　平移抛物线，记平移后点A的对应点为A′，点B的对应点为B′，点C(-2，0)和点D(-4，0)是x轴上的两个定点．‎ ‎①　当抛物线向左平移到某个位置时，A′C+CB′ 最短，求此时抛物线的函数解析式；‎ ‎②　当抛物线向左或向右平移时，是否存在某个位置，使四边形A′B′CD的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由．‎ ‎(第24题)‎ ‎4‎ x ‎2‎ ‎2‎ A ‎8‎ ‎-2‎ O ‎-2‎ ‎-4‎ y ‎6‎ B C D ‎-4‎ ‎4‎ ‎【040】△与△是两个直角边都等于厘米的等腰直角三角形，M、N分别是直角边AC、BC的中点。△位置固定，△按如图叠放，使斜边在直线MN上,顶点与点M重合。等腰直角△以‎1厘米/秒的速度沿直线MN向右平移，直到点与点N重合。设秒时，△与△重叠部分面积为平方厘米。‎ ‎（1）当△与△重叠部分面积为平方厘米时，求△移动的时间；‎ ‎（2）求与的函数关系式；‎ ‎（3）求△与△重叠部分面积的最大值。‎ ‎【041】某公交公司的公共汽车和出租车每天从乌鲁木齐市出发往返于乌鲁木齐市和石河子市两地，出租车比公共汽车多往返一趟，如图表示出租车距乌鲁木齐市的路程（单位：千米）与所用时间（单位：小时）的函数图象．已知公共汽车比出租车晚1小时出发，到达石河子市后休息2小时，然后按原路原速返回，结果比出租车最后一次返回乌鲁木齐早1小时．‎ ‎（1）请在图中画出公共汽车距乌鲁木齐市的路程（千米）与所用时间（小时）的函数图象．‎ ‎（2）求两车在途中相遇的次数（直接写出答案）‎ ‎（3）求两车最后一次相遇时，距乌鲁木齐市的路程．‎ ‎[来源:Zxxk.Com]‎y（千米）‎ x（小时）‎ ‎150‎ ‎100‎ ‎50‎ ‎1‎ ‎1‎ ‎0‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎【042】如图9，在矩形中，已知、两点的坐标分别为，为的中点．设点是平分线上的一个动点（不与点重合）．‎ ‎（1）试证明：无论点运动到何处，总与相等；‎ ‎（2）当点运动到与点的距离最小时，试确定过三点的抛物线的解析式；‎ ‎（3）设点是（2）中所确定抛物线的顶点，当点运动到何处时，的周长最小？求出此时点的坐标和的周长；‎ y O x P D B 图9‎ ‎（4）设点是矩形的对称中心，是否存在点，使？若存在，请直接写出点的坐标．‎ ‎【043】已知函数为方程的两个根，点在函数的图象上．‎ ‎（Ⅰ）若，求函数的解析式；‎ ‎（Ⅱ）在（Ⅰ）的条件下，若函数与的图象的两个交点为，当的面积为时，求的值；‎ ‎（Ⅲ）若，当时，试确定三者之间的大小关系，并说明理由．‎ ‎【044】如图9，已知抛物线y=x2–2x＋1的顶点为P，A为抛物线与y轴的交点，过A与y轴垂直的直线与抛物线的另一交点为B，与抛物线对称轴交于点O′，过点B和P的直线l交y轴于点C，连结O′C，将△ACO′沿O′C翻折后，点A落在点D的位置．‎ ‎(1) 求直线l的函数解析式；‎ ‎(2) 求点D的坐标；‎ ‎(3) 抛物线上是否存在点Q，使得S△DQC= S△DPB? 若存在，求出所有符合条件的点Q的坐标；若不存在，请说明理由．‎ 图9‎ ‎【045】如图，已知直线与轴交于点A，与轴交于点D，抛物线与直线交于A、E两点，与轴交于B、C两点，且B点坐标为 (1，0)。‎ ‎⑴求该抛物线的解析式；‎ ‎⑵动点P在轴上移动，当△PAE是直角三角形时，求点P的坐标P。‎ ‎⑶在抛物线的对称轴上找一点M，使的值最大，求出点M的坐标。‎ ‎【046】如图，已知直线与直线相交于点分别交轴于两点．矩形的顶点分别在直线上，顶点都在轴上，且点与点重合．‎ ‎ （1）求的面积；‎ ‎（2）求矩形的边与的长；‎ A D B E O C F x y y ‎（G）‎ ‎（3）若矩形从原点出发，沿轴的反方向以每秒1个单位长度的速度平移，设移动时间为秒，矩形与重叠部分的面积为，求关于的函数关系式，并写出相应的的取值范围．‎ ‎[来源:学科 ‎【047】如图（1），将正方形纸片折叠，使点落在边上一点（不与点，重合），压平后得到折痕．当时，求的值．‎ 方法指导：‎ 为了求得的值，可先求、的长，不妨设：=2‎ 类比归纳 在图（1）中，若则的值等于 ；若则的值等于 ；若（为整数），则的值等于 ．（用含的式子表示）‎ 联系拓广 图（2）‎ N A B C D E F M 图（1）‎ A B C D E F M N ‎ 如图（2），将矩形纸片折叠，使点落在边上一点（不与点重合），压平后得到折痕设则的值等于 ．（用含的式子表示）‎ ‎【048】如图11，抛物线与轴相交于A、B两点（点A在点B右侧），过点A的直线交抛物线于另一点C，点C的坐标为（-2，6）.‎ ‎(1)求a的值及直线AC的函数关系式；‎ ‎(2)P是线段AC上一动点，过点P作y轴的平行线，交抛物线于点M，交x轴于点N.‎ ‎①求线段PM长度的最大值；‎ ‎②在抛物线上是否存在这样的点M，使得△CMP与△APN相似？如果存在，请直接写出所有满足条件的点M的坐标（不必写解答过程）；如果不存在，请说明理由。 ‎ ‎【049】已知：抛物线的对称轴为与轴交于两点，与轴交于点其中、‎ ‎（1）求这条抛物线的函数表达式．‎ ‎（2）已知在对称轴上存在一点P，使得的周长最小．请求出点P的坐标．‎ ‎（3）若点是线段上的一个动点（不与点O、点C重合）．过点D作交轴于点连接、．设的长为，的面积为．求与之间的函数关系式．试说明是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．‎ ‎[来源:学科网]‎ A C x y B O ‎【050】如图，在梯形ABCD中，，，，，点由B出发沿BD方向匀速运动，速度为‎1cm/s；同时，线段EF由DC出发沿DA方向匀速运动，速度为‎1cm/s，交于Q，连接PE．若设运动时间为（s）（）．解答下列问题：‎ ‎（1）当为何值时，？‎ ‎（2）设的面积为（cm2），求与之间的函数关系式；‎ ‎（3）是否存在某一时刻，使？若存在，求出此时的值；若不存在，说明理由．‎ ‎（4）连接，在上述运动过程中，五边形的面积是否发生变化？说明理由．‎ A E D Q P B F C ‎【051】如图14（1），抛物线与x轴交于A、B两点，与y轴交于点C（0，）．［图14（2）、图14（3）为解答备用图］‎ ‎（1）　　　　　，点A的坐标为　　　　　　，点B的坐标为　　　　　；‎ ‎（2）设抛物线的顶点为M，求四边形ABMC的面积；‎ ‎（3）在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由；‎ ‎（4）在抛物线上求点Q，使△BCQ是以BC为直角边的直角三角形．‎ 图14（1）　　　　　　图14（2）　　　　　　　　图14（3）‎ ‎【052】已知二次函数（）的图象经过点，，，直线（）与轴交于点．‎ ‎（1）求二次函数的解析式；‎ ‎（2）在直线（）上有一点（点在第四象限），使得为顶点的三角形与以为顶点的三角形相似，求点坐标（用含的代数式表示）；‎ ‎（3）在（2）成立的条件下，抛物线上是否存在一点，使得四边形为平行四边形？若存在，请求出的值及四边形的面积；若不存在，请说明理由．‎ y x O ‎【053】如图所示，在平面直角坐标系中，抛物线（）经过，，三点，其顶点为，连接，点是线段上一个动点（不与重合），过点作轴的垂线，垂足为，连接．‎ ‎（1）求抛物线的解析式，并写出顶点的坐标；‎ ‎（2）如果点的坐标为，的面积为，求与的函数关系式，写出自变量的取值范围，并求出的最大值；‎ ‎1‎ ‎2‎ ‎3‎ ‎3‎ ‎1‎ D y C B A P ‎2‎ E x O ‎（3）在（2）的条件下，当取得最大值时，过点作的垂线，垂足为，连接，把沿直线折叠，点的对应点为，请直接写出点坐标，并判断点是否在该抛物线上．‎ ‎【054】如图，在直角坐标系中，矩形ABCD的边AD在y轴正半轴上，点A、C的坐标分 别为（0，1）、（2，4）．点P从点A出发，沿A→B→C以每秒1个单位的速度运动，到 点C停止；点Q在x轴上，横坐标为点P的横、纵坐标之和．抛物线 经过A、C两点．过点P作x轴的垂线，垂足为M，交抛物线于点R．设点P的运动时间为t（秒），△PQR的面积为S（平方单位）．‎ ‎（1）求抛物线对应的函数关系式．‎ ‎（2）分别求t=1和t=4时，点Q的坐标．‎ ‎（3）当0＜≤5时，求S与t之间的函数关系式，并直接写出S的最大值．‎ ‎【055】在平面直角坐标系中，现将一块等腰直角三角板放在第二象限，斜靠在两坐标轴上，且点，点，如图所示：抛物线经过点．‎ ‎（1）求点的坐标；‎ ‎（2）求抛物线的解析式；‎ ‎（3）在抛物线上是否还存在点（点除外），使仍然是以为直角边的等腰直角三角形？若存在，求所有点的坐标；若不存在，请说明理由．‎ B A C x y ‎（0，2）‎ ‎（－1，0）‎ ‎【056】如图18，抛物线F：的顶点为P，抛物线：与y轴交于点A，与直线OP交于点B．过点P作PD⊥x轴于点D，平移抛物线F使其经过点A、D得到抛物线F′：，抛物线F′与x轴的另一个交点为C．‎ ‎⑴当a = 1，b=－2，c = 3时，求点C的坐标(直接写出答案)；‎ ‎⑵若a、b、c满足了 ‎①求b：b′的值；‎ ‎②探究四边形OABC的形状，并说明理由．‎ 图 18‎ ‎【057】直线与坐标轴分别交于、两点，、的长分别是方程的两根（），动点从点出发，沿路线→→以每秒1个单位长度的速度运动，到达点时运动停止． ‎ ‎（1）直接写出、两点的坐标；‎ ‎（2）设点的运动时间为(秒)，的面积为，求与之间的函数关系式（不必写出自变量的取值范围）；‎ ‎（3）当时，直接写出点的坐标，此时，在坐标轴上是否存在点，使以、、、为顶点的四边形是梯形？若存在，请直接写出点的坐标；若不存在，请说明理由．‎ ‎ ‎ ‎【058】如图，已知抛物线与轴交于A、B两点，与轴交于点C．‎ ‎（1）求A、B、C三点的坐标．‎ ‎（2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．‎ C P B y A ‎（3）在轴上方的抛物线上是否存在一点M，过M作MG轴于点G，使以A、M、G三点为顶点的三角形与PCA相似．若存在，请求出M点的坐标；否则，请说明理由．‎ ‎ ‎ ‎【059】如图（1），已知正方形ABCD在直线MN的上方，BC在直线MN上，E是BC上一点，以AE为边在直线MN的上方作正方形AEFG．‎ ‎（1）连接GD，求证：△ADG≌△ABE；(4分)‎ ‎（2）连接FC，观察并猜测∠FCN的度数，并说明理由；(4分)‎ ‎（3）如图（2），将图（1）中正方形ABCD改为矩形ABCD，AB=a，BC=b（a、b为常数），E是线段BC上一动点（不含端点B、C），以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当点E由B向C运动时，∠FCN的大小是否总保持不变，若∠FCN的大小不变，请用含a、b的代数式表示tan∠FCN的值；若∠FCN的大小发生改变，请举例说明．(5分)‎ 图（2）‎ M B E A C D F G N N M B E C D F G 图（1）‎ ‎【060】已知：如图所示，关于的抛物线与轴交于点、点，与轴交于点．‎ ‎（1）求出此抛物线的解析式，并写出顶点坐标；‎ ‎（2）在抛物线上有一点，使四边形为等腰梯形，写出点的坐标，并求出直线的解析式；‎ B A O C y x ‎（3）在（2）中的直线交抛物线的对称轴于点，抛物线上有一动点，轴上有一动点．是否存在以为顶点的平行四边形？如果存在，请直接写出点的坐标；如果不存在，请说明理由．‎ ‎【061】如图已知直线L：，它与x轴、y轴的交点分别为A、B两点。‎ ‎（1）求点A、点B的坐标。‎ ‎（2）设F为x轴上一动点，用尺规作图作出⊙P，使⊙P经过点B且与x轴相切于点F（不写作法，保留作图痕迹）。‎ ‎（3）设92）中所作的⊙P的圆心坐标为P（x，y），求y关于x的函数关系式。‎ ‎（4）是否存在这样的⊙P，既与x轴相切又与直线L相切于点B，若存在，求出圆心P的坐标，若不存在，请说明理由。‎ ‎【062】如图13-1至图13-5，⊙O均作无滑动滚动，⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置，⊙O的周长为c．‎ 阅读理解：‎ 图13-1‎ A O1‎ O O2‎ B B 图13-2‎ A ‎ C n°‎ D O1‎ O2‎ B 图13-3‎ O2‎ O3‎ O A ‎ O1‎ C O4‎ ‎（1）如图13-1，⊙O从⊙O1的位置出发，沿AB滚动到 ‎⊙O2的位置，当AB = c时，⊙O恰好自转1周．‎ ‎（2）如图13-2，∠ABC相邻的补角是n°，⊙O在 ‎∠ABC外部沿A-B-C滚动，在点B处，必须由 ‎⊙O1的位置旋转到⊙O2的位置，⊙O绕点B旋 转的角∠O1BO2 = n°，⊙O在点B处自转周．‎ 实践应用：‎ ‎（1）在阅读理解的（1）中，若AB = ‎2c，则⊙O自 转 周；若AB = l，则⊙O自转 周．在 阅读理解的（2）中，若∠ABC = 120°，则⊙O 在点B处自转 周；若∠ABC = 60°，则⊙O 在点B处自转 周．‎ ‎（2）如图13-3，∠ABC=90°，AB=BC=c．⊙O从 ‎⊙O1的位置出发，在∠ABC外部沿A-B-C滚动 到⊙O4的位置，⊙O自转 周．‎ O A B C 图13-4‎ D 拓展联想：‎ ‎（1）如图13-4，△ABC的周长为l，⊙O从与AB相切于点D的位置出发，在△ABC外部，按顺时针方向沿三角形滚动，又回到与AB相切于点D的位置，⊙O自转了多少周？请说明理由．‎ ‎（2）如图13-5，多边形的周长为l，⊙O从与某边相切于 D 图13-5‎ O 点D的位置出发，在多边形外部，按顺时针方向沿多 边形滚动，又回到与该边相切于点D的位置，直接写 出⊙O自转的周数．‎ ‎【063】如图12，已知抛物线交轴于A、B两点，交 轴于点C，抛物线的对称轴交轴于点E，点B的坐标为（，0）．‎ ‎（1）求抛物线的对称轴及点A的坐标；‎ ‎（2）在平面直角坐标系中是否存在点P，与A、B、C三点构成一个平行四边形？若存在，请写出点P的坐标；若不存在，请说明理由；‎ O D B C A E 图12‎ ‎（3）连结CA与抛物线的对称轴交于点D，在抛物线上是否存在点M，使得直线CM把四边形DEOC分成面积相等的两部分？若存在，请求出直线CM的解析式；若不存在，请说明理由．‎ B O A ‎·‎ x y ‎【064】如图，抛物线的顶点为A，与y 轴交于点B．‎ ‎（1）求点A、点B的坐标．‎ ‎（2）若点P是x轴上任意一点，求证：．‎ ‎（3）当最大时，求点P的坐标． ‎ ‎【065】如图11，AB是⊙O的直径，弦BC=‎2cm，∠ABC=60º．‎ ‎ （1）求⊙O的直径；‎ ‎（2）若D是AB延长线上一点，连结CD，当BD长为多少时，CD与⊙O相切；‎ ‎（3）若动点E以‎2cm/s的速度从A点出发沿着AB方向运动，同时动点F以‎1cm/s的速度从B点出发沿BC方向运动，设运动时间为，连结EF，当为何值时，△BEF为直角三角形．‎ 图10（3）‎ A B C O E F A B C O D 图10（1）‎ A B O E F C 图10（2）‎ ‎【066】如图，反比例函数y＝(x＞0)的图象与一次函数y＝－x＋的图象交于A、B两点，点C的坐标为(1，)，连接AC，AC∥y轴．‎ ‎(1)求反比例函数的解析式及点B的坐标；‎ ‎(2)现有一个直角三角板，让它的直角顶点P在反比例函数图象上A、B之间的部分滑动(不与A、B重合)，两直角边始终分别平行于x轴、y轴，且与线段AB交于M、N两点，试判断P点在滑动过程中△PMN是否与△CBA总相似？简要说明判断理由．‎ ‎【067】如图，在直角梯形ABCD中，AD∥BC，∠ABC＝90º，AB＝‎12cm，AD＝‎8cm，BC＝‎22cm，AB为⊙O的直径，动点P从点A开始沿AD边向点D以‎1cm/s的速度运动，动点Q从点C开始沿CB边向点B以‎2cm/s的速度运动，P、Q分别从点A、C同时出发，当其中一点到达端点时，另一个动点也随之停止运动．设运动时间为t(s)．‎ ‎(1)当t为何值时，四边形PQCD为平行四边形？‎ ‎(2)当t为何值时，PQ与⊙O相切？‎ A B O C D P Q ‎【068】如图12，在直角梯形OABC中， OA∥‎ CB，A、B两点的坐标分别为A（15，0），B（10，12），动点P、Q分别从O、B两点出发，点P以每秒2个单位的速度沿OA向终点A运动，点Q以每秒1个单位的速度沿BC向C运动，当点P停止运动时，点Q也同时停止运动．线段OB、PQ相交于点D，过点D作DE∥OA，交AB于点E，射线QE交轴于点F．设动点P、Q运动时间为t（单位：秒）．‎ ‎（1）当t为何值时，四边形PABQ是等腰梯形，请写出推理过程；‎ ‎（2）当t=2秒时，求梯形OFBC的面积；‎ ‎（3）当t为何值时，△PQF是等腰三角形？请写出推理过程．‎ ‎069】如图11，已知二次函数的图象与轴相交于两个不同的点、，与轴的交点为．设的外接圆的圆心为点．‎ ‎（1）求与轴的另一个交点D的坐标；‎ ‎（2）如果恰好为的直径，且的面积等于，求和的值． ‎ ‎【070】如图所示，菱形的边长为‎6厘米，．从初始时刻开始，点、同时从点出发，点以‎1厘米/秒的速度沿的方向运动，点以‎2厘米/秒的速度沿的方向运动，当点运动到点时，、两点同时停止运动，设、运动的时间为秒时，与重叠部分的面积为平方厘米（这里规定：点和线段是面积为的三角形），解答下列问题： ‎ ‎（1）点、从出发到相遇所用时间是 秒；‎ ‎（2）点、从开始运动到停止的过程中，当是等边三角形时的值是 秒；‎ ‎（3）求与之间的函数关系式．‎ P Q A B C D ‎【071】已知：抛物线的对称轴为与轴交于两点，与轴交于点其中、‎ ‎（1）求这条抛物线的函数表达式．‎ ‎（2）已知在对称轴上存在一点P，使得的周长最小．请求出点P的坐标．‎ ‎（3）若点是线段上的一个动点（不与点O、点C重合）．过点D作交轴于点连接、．设的长为，的面积为．求与之间的函数关系式．试说明是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．‎ A C x y B O ‎【072】如图1所示，直角梯形OABC的顶点A、C分别在y轴正半轴与轴负半轴上.过点B、C作直线．将直线平移，平移后的直线与轴交于点D，与轴交于点E．‎ ‎（1）将直线向右平移，设平移距离CD为(t0)，直角梯形OABC被直线 扫过的面积（图中阴影部份）为，关于的函数图象如图2所示， OM为线段，MN为抛物线的一部分，NQ为射线，N点横坐标为4．‎ ‎①求梯形上底AB的长及直角梯形OABC的面积；‎ ‎②当时，求S关于的函数解析式；‎ ‎（2）在第（1）题的条件下，当直线向左或向右平移时（包括与直线BC重合），在直线AB上是否存在点P，使为等腰直角三角形?若存在，请直接写出所有满足条件的点P的坐标;若不存在，请说明理由．‎ ‎ ‎ ‎【073】)如图，半径为2的⊙O内有互相垂直的两条弦AB、CD相交于P点．‎ ‎(1)求证：PA·PB=PC·PD；‎ ‎(2)设BC的中点为F，连结FP并延长交AD于E，求证：EF⊥AD：‎ ‎(3)若AB=8，CD=6，求OP的长．‎ ‎【074】如图，在平面直角坐标系中，点的坐标为，以点为圆心，8为半径的圆与轴交于两点，过作直线与轴负方向相交成60°的角，且交轴于点，以点为圆心的圆与轴相切于点．‎ ‎（1）求直线的解析式；‎ O y x C D B A O1‎ O2‎ ‎60°‎ ‎（第22题）‎ l ‎（2）将以每秒1个单位的速度沿轴向左平移，当第一次与外切时，求平移的时间．‎ ‎【075】如图11，已知抛物线（）与轴的一个交点为，与y轴的负半轴交于点C，顶点为D．‎ ‎（1）直接写出抛物线的对称轴，及抛物线与轴的另一个交点A的坐标；‎ ‎（2）以AD为直径的圆经过点C．‎ ‎①求抛物线的解析式；‎ ‎②点在抛物线的对称轴上，点在抛物线上，且以四点为顶点的四边形为平行四边形，求点的坐标． ‎ O x y A B C D 图11‎ ‎【076】如图，抛物线与x轴交于A、B两点，与y轴交于C点，四边形OBHC为矩形，CH的延长线交抛物线于点D（5，2），连结BC、AD.‎ ‎（1）求C点的坐标及抛物线的解析式；‎ ‎（2）将△BCH绕点B按顺时针旋转90°后 再沿x轴对折得到 ‎△BEF（点C与点E对应），判断点E是否落在抛物线上，并说明理由；‎ ‎（3）设过点E的直线交AB边于点P，交CD边于点Q. 问是否存在点P，使直线PQ分梯形ABCD的面积为1∶3两部分？若存在，求出P点坐标；若不存在，请说明理由.‎ ‎【077】已知直线与轴轴分别交于点A和点B，点B的坐标为（0，6）‎ ‎（1）求的值和点A的坐标；‎ ‎（2）在矩形OACB中，点P是线段BC上的一动点，直线PD⊥AB于点D，与轴交于点E，设BP=，梯形PEAC的面积为。‎ ‎①求与的函数关系式，并写出的取值范围；‎ ‎②⊙Q是△OAB的内切圆，求当PE与⊙Q相交的弦长为2.4时点P的坐标。‎ ‎【078】如图 12，已知直线过点和，是轴正半轴上的动点，的垂直平分线交于点，交轴于点． ‎ ‎（1）直接写出直线的解析式； ‎ ‎（2）设，的面积为，求关于t的函数关系式；并求出当时，的最大值； ‎ L A O M P B x y L1‎ 图12‎ Q ‎（3）直线过点且与轴平行，问在上是否存在点， 使得是以为直角顶点的等腰直角三角形？若存在，求出点C的坐标，并证明；若不存在，请说明理由．‎ ‎【079】如图，在平面直角坐标系中，若、的长是关于的一元二次方程的两个根，且 ‎ （1）求的值．‎ ‎ （2）若为轴上的点，且求经过、两点的直线的解析式，并判断与是否相似？‎ ‎ （3）若点在平面直角坐标系内，则在直线上是否存在点使以、、、‎ 为顶点的四边形为菱形？若存在，请直接写出点的坐标；若不存在，请说明理由．‎ x y A D B O C ‎【080】已知：等边三角形的边长为‎4厘米，长为‎1厘米的线段在的边上沿方向以‎1厘米/秒的速度向点运动（运动开始时，点与点重合，点到达点时运动终止），过点分别作边的垂线，与的其它边交于两点，线段运动的时间为秒．‎ ‎（1）线段在运动的过程中，为何值时，四边形恰为矩形？并求出该矩形的面积；‎ C P Q B A M N ‎（2）线段在运动的过程中，四边形的面积为，运动的时间为．求四边形的面积随运动时间变化的函数关系式，并写出自变量的取值范围．‎ ‎【081】如图，已知抛物线y＝x2＋bx＋c与坐标轴交于A、B、C三点， A点的坐标为（－1，0），过点C的直线y＝x－3与x轴交于点Q，点P是线段BC上的一个动点，过P作PH⊥OB于点H．若PB＝5t，且0＜t＜1．‎ ‎（1）填空：点C的坐标是_▲_，b＝_▲_，c＝_▲_；‎ ‎（2）求线段QH的长（用含t的式子表示）；‎ ‎（3）依点P的变化，是否存在t的值，使以P、H、Q为顶点的三角形与△COQ相似？若存在，求出所有t的值；若不存在，说明理由．‎ ‎【082】C M O x y ‎1‎ ‎2‎ ‎3‎ ‎4‎ 图7‎ A ‎1‎ B D （09上海）在直角坐标平面内，为原点，点的坐标为，点的坐标为，直线 轴（如图7所示）．点与点关于原点对称，直线（为常数）经过点，且与直线相交于点，联结．‎ ‎（1）求的值和点的坐标；‎ ‎（2）设点在轴的正半轴上，若是等腰三角形，求点的坐标；‎ ‎（3）在（2）的条件下，如果以为半径的圆与圆外切，求圆的半径．‎ ‎【083】如图，在直角坐标系中，点A的坐标为（－2，0），连结OA，将线段OA绕原点O顺时针旋转120°，得到线段OB.‎ ‎（1）求点B的坐标；‎ ‎（2）求经过A、O、B三点的抛物线的解析式；‎ ‎（3）在（2）中抛物线的对称轴上是否存在点C，使△BOC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由.‎ B A O y x ‎（4）如果点P是（2）中的抛物线上的动点，且在x轴的下方，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由.‎ ‎【084】如图，在平面直角坐标系中，直线l：y=－2x－8分别与x轴，y轴相交于A，B两点，点P（0，k）是y轴的负半轴上的一个动点，以P为圆心，3为半径作⊙P.‎ ‎（1）连结PA，若PA=PB，试判断⊙P与x轴的位置关系，并说明理由；‎ ‎（2）当k为何值时，以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形？‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 【085】如图①， 已知抛物线（a≠0）与轴交于点A(1，0)和点B (－3，0)，与y轴交于点C．‎ ‎(1) 求抛物线的解析式；‎ ‎(2) 设抛物线的对称轴与轴交于点M ，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．‎ ‎(3) 如图②，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．‎ ‎【086】如图，以BC为直径的⊙O交△CFB的边CF于点A，BM平分 ‎∠ABC交AC于点M，AD⊥BC于点D，AD交BM于点N，ME⊥BC于点E，AB2=AF·AC，cos∠ABD=，AD=12．‎ ‎⑴求证：△ANM≌△ENM；‎ ‎⑵求证：FB是⊙O的切线；‎ ‎⑶证明四边形AMEN是菱形，并求该菱形的面积S．‎ ‎【087】如图，已知抛物线y＝x2＋bx＋c经过矩形ABCD的两个顶点A、B，AB平行于x轴，对角线BD与抛物线交于点P，点A的坐标为(0，2)，AB＝4．‎ ‎(1)求抛物线的解析式；‎ ‎(2)若S△APO＝，求矩形ABCD的面积．‎ A B C D y P x O ‎(第23题图)‎ ‎【088】如图所示，已知在直角梯形中，轴于点．动点从点出发，沿轴正方向以每秒1个单位长度的速度移动．过点作垂直于直线，垂足为．设点移动的时间为秒（），与直角梯形重叠部分的面积为．‎ ‎（1）求经过三点的抛物线解析式；‎ ‎（2）求与的函数关系式；‎ ‎（3）将绕着点顺时针旋转，是否存在，使得的顶点或在抛物线上？若存在，直接写出的值；若不存在，请说明理由．‎ ‎2‎ O A B C x y ‎1‎ ‎1‎ ‎3‎ P 第26题图 Q ‎【089】如图，在平面直角坐标系中，半径为1的圆的圆心在坐标原点，且与两坐标轴分别交于四点．抛物线与轴交于点，与直线交于点，且分别与圆相切于点和点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）抛物线的对称轴交轴于点，连结，并延长交圆于，求的长．‎ ‎（3）过点作圆的切线交的延长线于点，判断点 是否在抛物线上，说明理由．‎ O x y N C D E F B M A ‎【090】如图（9）-1，抛物线经过A（，0），C（3，）两点，与轴交于点D，与轴交于另一点B．‎ ‎（1）求此抛物线的解析式；‎ ‎（2）若直线将四边形ABCD面积二等分，求的值；‎ ‎（3）如图（9）-2，过点E（1，1）作EF⊥轴于点F，将△AEF绕平面内某点旋转180°得△MNQ（点M、N、Q分别与点A、E、F对应），使点M、N在抛物线上，作MG⊥轴于点G，若线段MG︰AG＝1︰2，求点M，N的坐标．‎ D O B A x y C y=kx+1‎ 图（9）-1‎ E F M N G O B A x y 图（9）-2‎ Q ‎【091】已知二次函数y＝x2－x＋c．‎ ‎(1)若点A(－1，a)、B(2，2n－1)在二次函数y＝x2－x＋c的图象上，求此二次函数的最小值；‎ ‎(2)若点D(x1，y1)、E(x2，y2)、P(m，n)(m＞n)在二次函数y＝x2－x＋c的图象上，且D、E两点关于坐标原点成中心对称，连接OP．当2≤OP≤2＋时，试判断直线DE与抛物线y＝x2－x＋c＋的交点个数，并说明理由．‎ ‎【092】已知：直角梯形OABC的四个顶点是O(0，0)，A(，1)， B(s，t)，C(，0)，抛物线y=x2＋mx－m的顶点P是直角梯形OABC内部或边上的一个动点，m为常数．‎ ‎(1)求s与t的值，并在直角坐标系中画出直角梯形OABC；‎ ‎(2)当抛物线y=x2＋mx－m与直角梯形OABC的边AB相交时，求m的取值范围．‎ ‎ ‎ ‎【093】已知在平面直角坐标系中，四边形OABC是矩形，点A、C的坐标分别为、，点D的坐标为，点P是直线AC上的一动点，直线DP与轴交于点M．问：‎ ‎（1）当点P运动到何位置时，直线DP平分矩形OABC的面积，请简要说明理由，并求出此时直线DP的函数解析式；‎ ‎（2）当点P沿直线AC移动时，是否存在使与相似的点M，若存在，请求出点M的坐标；若不存在，请说明理由；‎ ‎（3）当点P沿直线AC移动时，以点P为圆心、半径长为R（R＞0）画圆，所得到的圆称为动圆P．若设动圆P的直径长为AC，过点D作动圆P的两条切线，切点分别为点E、F．请探求是否存在四边形DEPF的最小面积S，若存在，请求出S的值；若不存在，请说明理由．‎ 注：第（3）问请用备用图解答．‎ 备用图 ‎【094】在平面直角坐标系中，已知，，且以为直径的圆交轴的正半轴于点，过点作圆的切线交轴于点．‎ ‎（1）求过三点的抛物线的解析式 ‎（2）求点的坐标 y x O C D B A ‎1‎ ‎2‎ ‎（3）设平行于轴的直线交抛物线于两点，问：是否存在以线段为直径的圆，恰好与轴相切？若存在，求出该圆的半径，若不存在，请说明理由？‎ ‎【095】）如图1，已知：抛物线与轴交于两点，与轴交于点，经过两点的直线是，连结．‎ ‎（1）两点坐标分别为（_____，_____）、（_____，_____），抛物线的函数关系式为______________；‎ ‎（2）判断的形状，并说明理由；‎ ‎（3）若内部能否截出面积最大的矩形（顶点在各边上）？若能，求出在边上的矩形顶点的坐标；若不能，请说明理由．‎ C A O B x y C A O B x y 图1‎ 图2(备用)‎ ‎[抛物线的顶点坐标是]‎ ‎【096】如图12，已知抛物线经过坐标原点O和x轴上另一点E，顶点M的坐标为 (2,4)；矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3.‎ ‎（1）求该抛物线所对应的函数关系式；‎ ‎（2）将矩形ABCD以每秒1个单位长度的速度从图12所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动，设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图13所示）. ‎ ‎① 当t=时，判断点P是否在直线ME上，并说明理由；‎ 图13‎ B C O A D E M y x P N ‎·‎ 图12‎ B C O ‎(A)‎ D E M y x ‎② 设以P、N、C、D为顶点的多边形面积为S，试问S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．‎ ‎【097】矩形在平面直角坐标系中位置如图13所示，两点的坐标分别为，，直线与边相交于点．‎ ‎（1）求点的坐标；‎ ‎（2）若抛物线经过点，试确定此抛物线的表达式；‎ y O C D B ‎6‎ A x 图13‎ ‎（3）设（2）中的抛物线的对称轴与直线交于点，点为对称轴上一动点，以为顶点的三角形与相似，求符合条件的点的坐标．‎ ‎【098】如图，在平面直角坐标系中，点A（0，6），点B是x轴上的一个动点，连结AB，取AB的中点M，将线段MB绕着点B按顺时针方向旋转90o，得到线段BC.过点B作x轴的垂线交直线AC于点D.设点B坐标是（t，0）.‎ ‎（1）当t=4时，求直线AB的解析式；‎ ‎（2）当t>0时，用含t的代数式表示点C的坐标及△ABC的面积；‎ ‎·‎ y O A x 备用图 M y O C A B x D ‎（3）是否存在点B,使△ABD为等腰三角形?若存在，请求出所有符合条件的点B的坐标；若不存在，请说明理由.‎ ‎【099】我们所学的几何知识可以理解为对“构图”的研究：根据给定的（或构造的）几何图形提出相关的概念和问题（或者根据问题构造图形），并加以研究.‎ 例如：在平面上根据两条直线的各种构图，可以提出“两条直线平行”、“两条直线相交”的概念；若增加第三条直线，则可以提出并研究“两条直线平行的判定和性质”等问题（包括研究的思想和方法）. ‎ 请你用上面的思想和方法对下面关于圆的问题进行研究：‎ ‎(1) 如图1，在圆O所在平面上，放置一条直线（和圆O分别交于点A、B），根据这个图形可以提出的概念或问题有哪些（直接写出两个即可）？‎ ‎(2) 如图2，在圆O所在平面上，请你放置与圆O都相交且不同时经过圆心的两条直线和（与圆O分别交于点A、B，与圆O分别交于点C、D）.‎ 请你根据所构造的图形提出一个结论，并证明之.‎ ‎(3) 如图3，其中AB是圆O的直径，AC是弦，D是ABC 的中点，弦DE⊥AB于点F. 请找出点C和点E重合的条件，并说明理由.‎ A B O m 题图1‎ O 题图2‎ A B O E 题图3‎ D C F G D C ‎【100】抛物线的顶点为M，与轴的交点为A、B（点B在点A的右侧），△ABM的三个内角∠M、∠A、∠B所对的边分别为m、a、b。若关于的一元二次方程有两个相等的实数根。‎ ‎（1）判断△ABM的形状，并说明理由。‎ ‎（2）当顶点M的坐标为（－2，－1）时，求抛物线的解析式，并画出该抛物线的大致图形。‎ ‎（3）若平行于轴的直线与抛物线交于C、D两点，以CD为直径的圆恰好与轴相切，求该圆的圆心坐标。‎ ‎【001】解：（1）抛物线经过点，‎ ‎ 1分 二次函数的解析式为： 3分 ‎（2）为抛物线的顶点过作于，则，‎ ‎ 4分 x y M C D P Q O A B N E H 当时，四边形是平行四边形 ‎ 5分 当时，四边形是直角梯形 过作于，则 ‎（如果没求出可由求）‎ ‎ 6分 当时，四边形是等腰梯形 综上所述：当、5、4时，对应四边形分别是平行四边形、直角梯形、等腰梯形． 7分 ‎（3）由（2）及已知，是等边三角形 则 过作于，则 8分 ‎= 9分 当时，的面积最小值为 10分 此时 A C ‎)‎ B P Q D 图3‎ E ‎)‎ F ‎ 11分 ‎【002】解：（1）1，； ‎ ‎（2）作QF⊥AC于点F，如图3， AQ = CP= t，∴．‎ A C B P Q E D 图4‎ 由△AQF∽△ABC，， ‎ 得．∴． ∴，‎ 即．‎ ‎（3）能．‎ A C B P Q E D 图5‎ A C(E)‎ ‎)‎ B P Q D 图6‎ G A C(E)‎ ‎)‎ B P Q D 图7‎ G ‎ ①当DE∥QB时，如图4．‎ ‎ ∵DE⊥PQ，∴PQ⊥QB，四边形QBED是直角梯形．‎ ‎ 此时∠AQP=90°．‎ 由△APQ ∽△ABC，得，‎ 即． 解得． ‎ ‎②如图5，当PQ∥BC时，DE⊥BC，四边形QBED是直角梯形．‎ 此时∠APQ =90°．‎ 由△AQP ∽△ABC，得 ，‎ 即． 解得． ‎ ‎（4）或．‎ ‎【注：①点P由C向A运动，DE经过点C．‎ 方法一、连接QC，作QG⊥BC于点G，如图6．‎ ‎，．‎ 由，得，解得．‎ 方法二、由，得，进而可得 ‎，得，∴．∴． ‎ ‎②点P由A向C运动，DE经过点C，如图7．‎ ‎，】‎ ‎【003】解.(1)点A的坐标为（4，8） …………………1分 将A (4,8)、C（8，0）两点坐标分别代入y=ax2+bx ‎ 8=‎16a+4b ‎ 得 ‎ ‎ 0=‎64a+8b ‎ 解 得a=-,b=4‎ ‎∴抛物线的解析式为：y=－x2+4x …………………3分 ‎（2）①在Rt△APE和Rt△ABC中，tan∠PAE==,即=‎ ‎∴PE=AP=t．PB=8-t．‎ ‎∴点Ｅ的坐标为（4+t，8-t）.‎ ‎∴点G的纵坐标为：－（4+t）2+4(4+t）=－t2+8. …………………5分 ‎∴EG=－t2+8-(8-t) =－t2+t.‎ ‎∵-＜0，∴当t=4时，线段EG最长为2. …………………7分 ‎②共有三个时刻. …………………8分 t1=， t2=，t3= ． …………………11分 ‎【004】（1）解：由得点坐标为 由得点坐标为∴（2分）‎ 由解得∴点的坐标为（3分）‎ ‎∴（4分）‎ ‎（2）解：∵点在上且 ∴点坐标为（5分）又∵点在上且∴点坐标为（6分）‎ ‎∴（7分）‎ ‎（3）解法一：当时，如图1，矩形与重叠部分为五边形（时，为四边形）．过作于，则 A D B E O R F x y y M ‎（图3）‎ G C A D B E O C F x y y G ‎（图1）‎ R M A D B E O C F x y y G ‎（图2）‎ R M ‎∴即∴‎ ‎∴‎ 即（10分）‎ 图1‎ A D E B F C G ‎【005】（1）如图1，过点作于点 1分 ‎∵为的中点，‎ ‎∴‎ 在中，∴ 2分 ‎∴‎ 即点到的距离为 3分 ‎（2）①当点在线段上运动时，的形状不发生改变．‎ ‎∵∴‎ ‎∵∴，‎ 同理 4分 如图2，过点作于，∵‎ 图2‎ A D E B F C P N M G H ‎∴‎ ‎∴‎ ‎∴‎ 则 在中，‎ ‎∴的周长= 6分 ‎②当点在线段上运动时，的形状发生改变，但恒为等边三角形．‎ 当时，如图3，作于，则 类似①，‎ ‎∴ 7分 ‎∵是等边三角形，∴‎ 此时， 8分 图3‎ A D E B F C P N M 图4‎ A D E B F C P M N 图5‎ A D E B F（P）‎ C M N G G R G ‎ 当时，如图4，这时 此时，‎ 当时，如图5，‎ 则又 ‎∴‎ 因此点与重合，为直角三角形．‎ ‎∴‎ 此时，‎ 综上所述，当或4或时，为等腰三角形． ‎ ‎【006】解：（1）OC=1,所以,q=-1,又由面积知0.5OC×AB=,得AB=，‎ ‎ 设A（a,0）,B(b,0)AB=b-a==，解得p=,但p<0,所以p=。‎ ‎ 所以解析式为：‎ ‎（2）令y=0，解方程得，得,所以A(,0),B(2,0),在直角三角形AOC中可求得AC=,同样可求得BC=，显然AC2+BC2=AB2，得△ABC是直角三角形。AB为斜边，所以外接圆的直径为AB=,所以。‎ ‎（3）存在，AC⊥BC，①若以AC为底边，则BD//AC,易求AC的解析式为y=-2x-1,可设BD的解析式为y=-2x+b，把B(2,0)代入得BD解析式为y=-2x+4，解方程组得D（，9）‎ ‎ ②若以BC为底边，则BC//AD,易求BC的解析式为y=0.5x-1,可设AD的解析式为y=0.5x+b，把 A(，0)代入得AD解析式为y=0.5x+0.25，解方程组得D() 综上，所以存在两点：（,9）或()。‎ ‎【007】‎ ‎【008】证明：（1）∵∠ABC=90°，BD⊥EC，‎ ‎∴∠1与∠3互余，∠2与∠3互余，‎ ‎∴∠1=∠2…………………………………………………1分 ‎∵∠ABC=∠DAB=90°，AB=AC ‎∴△BAD≌△CBE…………………………………………2分 ‎∴AD=BE……………………………………………………3分 ‎（2）∵E是AB中点，‎ ‎∴EB=EA由（1）AD=BE得：AE=AD……………………………5分 ‎∵AD∥BC∴∠7=∠ACB=45°∵∠6=45°∴∠6=∠7‎ 由等腰三角形的性质，得：EM=MD，AM⊥DE。‎ 即，AC是线段ED的垂直平分线。……………………7分 ‎（3）△DBC是等腰三角（CD=BD）……………………8分 理由如下：‎ 由（2）得：CD=CE由（1）得：CE=BD∴CD=BD ‎∴△DBC是等腰三角形。……………………………10分 ‎【009】O C F M D E N K y x 图1‎ 解：（1）①轴，轴，‎ 四边形为矩形．‎ 轴，轴，‎ 四边形为矩形．‎ 轴，轴，‎ 四边形均为矩形． 1分 ‎，‎ ‎，‎ ‎．‎ ‎．‎ ‎，‎ ‎ ，‎ ‎． 2分 ‎②由（1）知．‎ ‎．‎ ‎． 4分 ‎，‎ ‎． 5分 ‎．‎ ‎． 6分 轴，‎ 四边形是平行四边形．‎ ‎． 7分 同理．‎ ‎． 8分 ‎（2）与仍然相等． 9分 ‎，‎ O C D K F E N y x M 图2‎ ‎，‎ 又，‎ ‎． 10分 ‎．‎ ‎．‎ ‎，‎ ‎．‎ ‎．‎ ‎． 11分 轴，‎ 四边形是平行四边形．‎ ‎．‎ 同理．‎ ‎． 12分 ‎【010】y x E D N O A C M P N ‎1‎ F ‎（第26题图）‎ 解：（1）根据题意，得 2分 解得抛物线对应的函数表达式为． 3分 ‎（2）存在．‎ 在中，令，得．‎ 令，得，．‎ ‎，，．‎ 又，顶点． 5分 容易求得直线的表达式是．‎ 在中，令，得．‎ ‎，． 6分 在中，令，得．‎ ‎．‎ ‎，四边形为平行四边形，此时． 8分 ‎（3）是等腰直角三角形．‎ 理由：在中，令，得，令，得．‎ 直线与坐标轴的交点是，．‎ ‎，． 9分 又点，．． 10分 由图知，． 11分 ‎，且．是等腰直角三角形． 12分 ‎（4）当点是直线上任意一点时，（3）中的结论成立． 14分 ‎【011】解：（1）证明：在Rt△FCD中，∵G为DF的中点，∴ CG= FD．………1分 同理，在Rt△DEF中，EG= FD．…………2分∴ CG=EG．…………………3分 ‎（2）（1）中结论仍然成立，即EG=CG．…………………………4分 证法一：连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点．‎ 在△DAG与△DCG中，∵ AD=CD，∠ADG=∠CDG，DG=DG，‎ ‎∴ △DAG≌△DCG．∴ AG=CG．………………………5分 在△DMG与△FNG中，∵ ∠DGM=∠FGN，FG=DG，∠MDG=∠NFG，‎ ‎∴ △DMG≌△FNG．∴ MG=NG 在矩形AENM中，AM=EN． ……………6分 在Rt△AMG 与Rt△ENG中，∵ AM=EN， MG=NG，‎ ‎∴ △AMG≌△ENG．∴ AG=EG．∴ EG=CG． ……………………………8分 证法二：延长CG至M,使MG=CG，‎ 连接MF，ME，EC， ……………………4分 在△DCG 与△FMG中，∵FG=DG，∠MGF=∠CGD，MG=CG，‎ ‎∴△DCG ≌△FMG．∴MF=CD，∠FMG＝∠DCG． ‎ ‎∴MF∥CD∥AB．………………………5分∴ 在Rt△MFE 与Rt△CBE中，‎ ‎∵ MF=CB，EF=BE，∴△MFE ≌△CBE．∴∠MEC＝∠MEF＋∠FEC＝∠CEB＋∠CEF＝90°．∴ △MEC为直角三角形．∵ MG = CG，∴ EG= MC．………8分 ‎（3）（1）中的结论仍然成立，即EG=CG．其他的结论还有:EG⊥CG．……10分 ‎【012】解：（1）圆心在坐标原点，圆的半径为1，‎ 点的坐标分别为 抛物线与直线交于点，且分别与圆相切于点和点，‎ ‎．点在抛物线上，将的坐标代入，得： 解之，得：‎ 抛物线的解析式为：． 4分 ‎（2）‎ 抛物线的对称轴为，‎ O x y N C D E F B M A P ‎． 6分 连结，‎ ‎，，‎ 又，‎ ‎，‎ ‎． 8分 ‎（3）点在抛物线上． 9分 设过点的直线为：，‎ 将点的坐标代入，得：，‎ 直线为：． 10分 过点作圆的切线与轴平行，点的纵坐标为，‎ 将代入，得：．‎ 点的坐标为，当时，，‎ 所以，点在抛物线上． 12分 ‎【013】解：（1）该抛物线过点，可设该抛物线的解析式为．‎ 将，代入，‎ 得解得 此抛物线的解析式为． （3分）‎ ‎（2）存在． （4分）‎ 如图，设点的横坐标为，‎ O x y A B C ‎4‎ ‎1‎ ‎（第26题图）‎ D P M E 则点的纵坐标为，‎ 当时，‎ ‎，．‎ 又，‎ ‎①当时，‎ ‎，‎ 即．‎ 解得（舍去），． （6分）‎ ‎②当时，，即．‎ 解得，（均不合题意，舍去）‎ 当时，． （7分）‎ 类似地可求出当时，． （8分）‎ 当时，．‎ 综上所述，符合条件的点为或或． （9分）‎ ‎（3）如图，设点的横坐标为，则点的纵坐标为．‎ 过作轴的平行线交于．由题意可求得直线的解析式为 ‎． （10分）‎ 点的坐标为．． （11分）‎ ‎．‎ 当时，面积最大．． （13分）‎ ‎【014】（1）解：∵点第一次落在直线上时停止旋转，∴旋转了.‎ ‎∴在旋转过程中所扫过的面积为.……………4分 ‎（2）解：∵∥，∴,.‎ ‎∴.∴.又∵，∴.‎ 又∵,,∴.∴.∴.∴旋转过程中，当和平行时，正方形旋转的度数为.……………………………………………8分 ‎（3）答：值无变化. 证明：延长交轴于点，则，‎ ‎，∴.又∵，.∴.∴. ‎ ‎（第26题）‎ O A B C M N 又∵,, ∴.‎ ‎∴.∴，‎ ‎∴.‎ ‎∴在旋转正方形的过程中，值无变化. ……………12分 ‎【015】⑴设二次函数的解析式为：y=a(x-h)2+k∵顶点C的横坐标为4，且过点(0，)‎ ‎∴y=a(x-4)2+k ………………①‎ 又∵对称轴为直线x=4，图象在x轴上截得的线段长为6 ∴A(1，0)，B(7，0)‎ ‎∴0=‎9a+k ………………②由①②解得a=，k=∴二次函数的解析式为：y=(x-4)2－‎ ‎⑵∵点A、B关于直线x=4对称 ∴PA=PB ∴PA+PD=PB+PD≥DB ∴当点P在线段DB上时PA+PD取得最小值 ∴DB与对称轴的交点即为所求点P 设直线x=4与x轴交于点M ∵PM∥OD，∴∠BPM=∠BDO，又∠PBM=∠DBO ‎∴△BPM∽△BDO∴ ∴∴点P的坐标为(4，)‎ ‎⑶由⑴知点C(4，)，又∵AM=3，∴在Rt△AMC中，cot∠ACM=，‎ ‎∴∠ACM=60o，∵AC=BC，∴∠ACB=120o ‎①当点Q在x轴上方时，过Q作QN⊥x轴于N 如果AB=BQ，由△ABC∽△ABQ有 BQ=6，∠ABQ=120o，则∠QBN=60o ∴QN=3，BN=3，ON=10，此时点Q(10，)，‎ 如果AB=AQ，由对称性知Q(-2，)‎ ‎②当点Q在x轴下方时，△QAB就是△ACB，此时点Q的坐标是(4，)，‎ 经检验，点(10，)与(-2，)都在抛物线上 ‎ 综上所述，存在这样的点Q，使△QAB∽△ABC ‎ 点Q的坐标为(10，)或(-2，)或(4，)．‎ ‎【016】解：（1）设正比例函数的解析式为，‎ 因为的图象过点，所以，解得．‎ 这个正比例函数的解析式为． （1分）‎ 设反比例函数的解析式为．因为的图象过点，所以 ‎，解得．这个反比例函数的解析式为． （2分）‎ ‎（2）因为点在的图象上，所以，则点． （3分）‎ 设一次函数解析式为．因为的图象是由平移得到的，‎ 所以，即．又因为的图象过点，所以 ‎，解得，一次函数的解析式为． （4分）‎ ‎（3）因为的图象交轴于点，所以的坐标为．‎ 设二次函数的解析式为．‎ 因为的图象过点、、和，‎ 所以 （5分） 解得 这个二次函数的解析式为． （6分）‎ ‎（4）交轴于点，点的坐标是，‎ y x O C D B A ‎3‎ ‎3‎ ‎6‎ E 如图所示，‎ ‎．‎ 假设存在点，使．‎ 四边形的顶点只能在轴上方，，‎ ‎ ．‎ ‎，．在二次函数的图象上，‎ ‎．解得或．‎ 当时，点与点重合，这时不是四边形，故舍去，‎ 点的坐标为． （8分）‎ ‎【017】解：（1）已知抛物线经过，‎ ‎ 解得 所求抛物线的解析式为． 2分 ‎（2），，‎ 可得旋转后点的坐标为 3分 当时，由得，‎ 可知抛物线过点 将原抛物线沿轴向下平移1个单位后过点．‎ 平移后的抛物线解析式为：． 5分 ‎（3）点在上，可设点坐标为 将配方得，其对称轴为． 6分 y x C B A O N D B1‎ D1‎ 图①‎ ‎①当时，如图①，‎ 此时 y x C B A O D B1‎ D1‎ 图②‎ N 点的坐标为． 8分 ‎②当时，如图②‎ 同理可得 此时 点的坐标为．‎ 综上，点的坐标为或． 10分 ‎【018】解：（1）抛物线经过，两点，‎ ‎ 解得 抛物线的解析式为．‎ y x O A B C D E ‎（2）点在抛物线上，，‎ 即，或．‎ 点在第一象限，点的坐标为．‎ 由（1）知．‎ 设点关于直线的对称点为点．‎ ‎，，且，‎ ‎，‎ 点在轴上，且．‎ ‎，．‎ 即点关于直线对称的点的坐标为（0，1）．‎ ‎（3）方法一：作于，于．‎ y x O A B C D E P F 由（1）有：，‎ ‎．‎ ‎，且．‎ ‎，‎ ‎．‎ ‎，，，‎ ‎．‎ 设，则，，‎ ‎．‎ 点在抛物线上，‎ ‎，‎ ‎（舍去）或，．‎ y x O A B C D P Q G H 方法二：过点作的垂线交直线于点，过点作轴于．过点作于．‎ ‎．‎ ‎，‎ 又，．‎ ‎，，．‎ 由（2）知，．‎ ‎，直线的解析式为．‎ 解方程组得 点的坐标为．‎ ‎【019】（1）EO＞EC，理由如下：‎ 由折叠知，EO=EF，在Rt△EFC中，EF为斜边，∴EF＞EC， 故EO＞EC …2分 ‎（2）m为定值 ‎∵S四边形CFGH=CF2=EF2－EC2=EO2－EC2=(EO+EC)(EO―EC)=CO·(EO―EC)‎ S四边形CMNO=CM·CO=|CE―EO|·CO=(EO―EC) ·CO ‎∴ ……………………………………………………4分 ‎（3）∵CO=1， ∴EF=EO=‎ ‎∴cos∠FEC= ∴∠FEC=60°，‎ ‎∴‎ ‎∴△EFQ为等边三角形， …………………………………………5分 作QI⊥EO于I，EI=，IQ=‎ ‎∴IO= ∴Q点坐标为 ……………………………………6分 ‎∵抛物线y=mx2+bx+c过点C(0，1)， Q ，m=1‎ ‎∴可求得，c=1‎ ‎∴抛物线解析式为 ……………………………………7分 ‎（4）由（3），‎ 当时，＜AB ‎∴P点坐标为 …………………8分 ‎∴BP=AO 方法1：若△PBK与△AEF相似，而△AEF≌△AEO，则分情况如下：‎ ‎①时，∴K点坐标为或 ‎②时， ∴K点坐标为或…………10分 故直线KP与y轴交点T的坐标为 ‎ …………………………………………12分 方法2：若△BPK与△AEF相似，由（3）得：∠BPK=30°或60°，过P作PR⊥y轴于R，则∠RTP=60°或30°‎ ‎①当∠RTP=30°时，‎ ‎②当∠RTP=60°时，‎ ‎∴ ……………………………12分 ‎【020】解：（1）①CF⊥BD，CF=BD ‎ ‎②成立，理由如下：∵∠FAD=∠BAC=90° ∴∠BAD=∠CAF 又 BA=CA ，AD=AF ∴△BAD≌△CAF∴CF=BD ∠ACF=∠ACB=45°‎ ‎∴∠BCF=90° ∴CF⊥BD ……（1分）‎ ‎（2）当∠ACB=45°时可得CF⊥BC，理由如下：‎ 如图：过点A作AC的垂线与CB所在直线交于G 则∵∠ACB=45° ∴AG=AC ∠AGC=∠ACG=45°‎ ‎∵AG=AC AD=AF ………（1分）‎ ‎∴△GAD≌△CAF（SAS） ∴∠ACF=∠AGD=45°‎ ‎∴∠GCF=∠GCA+∠ACF=90° ∴CF⊥BC …………（2分）‎ ‎（3）如图：作AQBC于Q ‎∵∠ACB=45° AC=4 ∴CQ=AQ=4‎ ‎∵∠PCD=∠ADP=90°∴∠ADQ+∠CDP=∠CDP+∠CPD=90°‎ ‎∴△ADQ∽△DPC …（1分）‎ ‎∴=‎ 设CD为x（0＜x＜3）则DQ=CQ－CD=4－x则= …………（1分）‎ ‎∴PC=(－x2+4x)=－(x－2)2+1≥1‎ 当x=2时，PC最长，此时PC=1 ………（1分）‎ ‎【021】解：（1）； … ………………………………3分 ‎（2）①EF∥AB． ……………………………………4分 证明：如图，由题意可得A（–4，0），B（0，3），， ．‎ ‎∴PA=3，PE=，PB=4，PF=．‎ ‎∴，‎ ‎∴． ………………………… 6分 ‎ 又∵∠APB=∠EPF．‎ ‎∴△APB ∽△EPF，∴∠PAB=∠PEF．‎ ‎∴EF∥AB． …………………………… 7分 ‎②S2没有最小值，理由如下：‎ 过E作EM⊥y轴于点M，过F作FN⊥x轴于点N，两线交于点Q．‎ 由上知M（0，），N（，0），Q（，）． ……………… 8分 而S△EFQ= S△PEF，∴S2＝S△PEF－S△OEF＝S△EFQ－S△OEF＝S△EOM＋S△FON＋S矩形OMQN ‎＝＝‎ ‎=． ………………………… 10分 当时，S2的值随k2的增大而增大，而0＜k2＜12． …………… 11分 ‎∴0＜S2＜24，s2没有最小值． …………………………… 12分 说明：1．证明AB∥EF时，还可利用以下三种方法．方法一：分别求出经过A、B两点和经过E、F两点的直线解析式，利用这两个解析式中x的系数相等来证明AB∥EF；方法二：利用＝来证明AB∥EF；方法三：连接AF、BE，利用S△AEF＝S△BFE得到点A、点B到直线EF的距离相等，再由A、B两点在直线EF同侧可得到AB∥EF．‎ ‎2．求S2的值时，还可进行如下变形：‎ S2＝ S△PEF－S△OEF＝S△PEF－（S四边形PEOF－S△PEF）＝2 S△PEF－S四边形PEOF，再利用第（1）题中的结论．‎ ‎【022】解：(1)设抛物线的解析式为：y＝a(x－m＋2)(x－m－2)＝a(x－m)2－‎4a．……2分 ‎∵AC⊥BC，由抛物线的对称性可知：△ACB是等腰直角三角形，又AB＝4，‎ ‎∴C(m，－2)代入得a＝．∴解析式为：y＝(x－m)2－2．………………………5分 ‎(亦可求C点，设顶点式)‎ ‎(2)∵m为小于零的常数，∴‎ 只需将抛物线向右平移－m个单位，再向上平移2个单位，可以使抛物线y＝(x－m)2－2顶点在坐标原点．……………………………………7分 ‎(3)由(1)得D(0，m2－2)，设存在实数m，使得△BOD为等腰三角形．‎ ‎∵△BOD为直角三角形，∴只能OD＝OB．……………………………………………9分 ‎∴m2－2＝|m＋2|，当m＋2＞0时，解得m＝4或m＝－2(舍)．‎ 当m＋2＜0时，解得m＝0(舍)或m＝－2(舍)；‎ 当m＋2＝0时，即m＝－2时，B、O、D三点重合(不合题意，舍)‎ 综上所述：存在实数m＝4，使得△BOD为等腰三角形．……………………………12分 A D C B P M Q ‎60°‎ ‎【023】（1）证明：∵是等边三角形 ‎∴‎ ‎∵是中点 ∴ ∵‎ ‎∴‎ ‎∴ ∴ ∴梯形是等腰梯形． ‎ ‎（2）解：在等边中，‎ ‎∴‎ ‎∴∴ ∴ 5分 ‎∵ ∴ 6分 ‎∴ ∴ 7分 ‎（3）解：①当时，则有 则四边形和四边形均为平行四边形∴‎ 当时，则有 ，‎ 则四边形和四边形均为平行四边形 ∴‎ ‎∴当或时，以P、M和A、B、C、 D中的两个点为顶点的四边形是平行四边形．此时平行四边形有4个．‎ 为直角三角形 ∵ ∴当取最小值时，‎ ‎∴是的中点，而∴∴‎ ‎【024】（1）由可知，，又△ABC为等腰直角三角形，‎ ‎∴，，所以点A的坐标是（）. ‎ ‎（2）∵ ∴，则点的坐标是（）.‎ 又抛物线顶点为，且过点、，所以可设抛物线的解析式为：，得： ‎ ‎ 解得 ∴抛物线的解析式为 ………7分 ‎（3）过点作于点，过点作于点，设点的坐标是，则，.‎ ‎∵ ∴∽ ∴ 即，得 ∵ ∴∽ ∴ 即，得 又∵‎ ‎∴‎ 即为定值8. ‎ ‎【025】解：（1）设点M的横坐标为x，则点M的纵坐标为－x+4（00，－x+4>0）；‎ ‎ 则：MC＝∣－x+4∣＝－x+4，MD＝∣x∣＝x；‎ ‎ ∴C四边形OCMD＝2（MC+MD）＝2（－x+4+x）＝8‎ ‎∴当点M在AB上运动时，四边形OCMD的周长不发生变化，总是等于8；‎ ‎（2）根据题意得：S四边形OCMD＝MC·MD＝（－x+4）· x＝－x2+4x＝－(x-2)2+4‎ ‎∴‎ 四边形OCMD的面积是关于点M的横坐标x（0PA，∴只存在点Q1,使Q‎1A=Q1P.‎ 如图2,过点Q1作Q‎1M⊥AP，垂足为点M，Q‎1M交AC于点F,则AM=.‎ 由△AMF∽△AOD∽△CQ‎1F,得, ,‎ ‎∴. ………………1分∴CQ1==.则,‎ ‎∴ .……………………………1分 第二种情况：当点Q在BA上时,存在两点Q2,Q3,‎ 分别使A P= A Q2,PA=PQ3.‎ ‎①若AP=AQ2，如图3,CB+BQ2=10-4=6.‎ 则,∴.……1分 ‎ ‎②若PA=PQ3，如图4,过点P作PN⊥AB，垂足为N，‎ 由△ANP∽△AEB,得. ‎ ‎∵AE= , ∴AN＝.‎ ‎∴AQ3=2AN=, ∴BC+BQ3=10-‎ 则.∴. ‎ ‎………………………1分 综上所述，当t= 4秒，以所得的等腰三角形APQ沿底边翻折，翻折后得到菱形的k值为或或.‎ ‎【032】解：（1）在△ABC中，∵，，．‎ ‎∴，解得．　 4分 ‎（2）①若AC为斜边，则，即，无解．‎ ‎②若AB为斜边，则，解得，满足．‎ ‎③若BC为斜边，则，解得，满足．‎ C A B N M ‎（第24题-1）‎ D ‎∴或．　 9分 ‎（3）在△ABC中，作于D，‎ 设，△ABC的面积为S，则．‎ ‎①若点D在线段AB上，‎ 则．‎ ‎∴，即．‎ ‎∴，即．‎ ‎∴（）．　 11分 当时（满足），取最大值，从而S取最大值． 13分 ‎②若点D在线段MA上，‎ C B A D M N ‎（第24题-2）‎ 则．‎ 同理可得，‎ ‎（），‎ 易知此时．‎ 综合①②得，△ABC的最大面积为． 14分 ‎【033】‎第（2）题 x y B C O D A M N N′‎ x y B C O A M N P1‎ P2‎ 备用图 ‎（1）.……………4分 ‎（2）由题意得点与点′关于轴对称，，‎ 将′的坐标代入得，‎ ‎（不合题意，舍去），.……………2分 ‎，点到轴的距离为3.‎ ‎， ，直线的解析式为，‎ 它与轴的交点为点到轴的距离为.‎ ‎.……………2分 ‎（3）当点在轴的左侧时，若是平行四边形，则平行且等于，‎ 把向上平移个单位得到，坐标为，代入抛物线的解析式，‎ 得：‎ ‎（不舍题意，舍去），，.……………2分 当点在轴的右侧时，若是平行四边形，则与互相平分，‎ ‎．‎ ‎ 与关于原点对称，，‎ 将点坐标代入抛物线解析式得：，‎ ‎（不合题意，舍去），，．……………2分 存在这样的点或，能使得以为顶点的四边形是平行四边形．‎ ‎【034】解：（1）2. ……………2分 A C B P E 第（25）题 ‎（2）证明：在上取点，使，‎ 连结，再在上截取，连结．‎ ‎，为正三角形，‎ ‎=，‎ 为正三角形，=，‎ ‎=，‎ ‎′，．‎ ‎，‎ ‎，为的费马点，‎ 过的费马点，且=+．………2分 ‎【035】解：（1）（1，0） 1分 ‎ 点P运动速度每秒钟1个单位长度． 2分 ‎（2） 过点作BF⊥y轴于点，⊥轴于点，则＝8，．‎ ‎ ∴．‎ ‎ 在Rt△AFB中， 3分 ‎ 过点作⊥轴于点，与的延长线交于点．‎ ‎∵ ∴△ABF≌△BCH． ‎ ‎ ∴． ‎ ‎∴．‎ ‎∴所求C点的坐标为（14，12）． 4分 ‎（3） 过点P作PM⊥y轴于点M，PN⊥轴于点N，‎ 则△APM∽△ABF．‎ ‎ ∴． ． ‎ ‎ ∴． ∴．‎ 设△OPQ的面积为（平方单位）‎ ‎∴（0≤≤10） 5分 说明:未注明自变量的取值范围不扣分．‎ ‎ ∵<0 ∴当时， △OPQ的面积最大． 6分 ‎ 此时P的坐标为（，） ． 7分 ‎（4） 当 或时， OP与PQ相等． 9分 ‎ 对一个加1分，不需写求解过程．‎ ‎【036】解：（1）由已知，得，，‎ ‎，‎ ‎．． （1分）‎ 设过点的抛物线的解析式为．将点的坐标代入，得．[来源:学&将和点的坐标分别代入，得 （2分）‎ 解这个方程组，得[来源:学#科#网]故抛物线的解析式为． （3分）‎ ‎（2）成立． （4分）‎ 点在该抛物线上，且它的横坐标为，y x D B C A E E O Ｍ F K G G 点的纵坐标为． （5分）‎ 设的解析式为，‎ 将点的坐标分别代入，得 ‎ 解得 的解析式为．，． （7分）‎ 过点作于点，则．，‎ ‎．又，．‎ ‎．[来．．‎ ‎（3）点在上，，，则设．‎ ‎，，．‎ ‎①若，则，‎ 解得．，此时点与点重合．．‎ ‎②若，则，解得 ，，此时轴．‎ 与该抛物线在第一象限内的交点的横坐标为1，点的纵坐标为．．‎ ‎③若，则，[来 解得，，此时，是等腰直角三角形．‎ 过点作轴于点，则，设，‎ y x D B C A E E O Q P H G G ‎(P)‎ ‎(Q)‎ Q ‎(P)‎ ‎．‎ ‎．‎ 解得（舍去）．．（12分）‎ 综上所述，存在三个满足条件的点，即或或．‎ ‎【037】解：（1）设第一象限内的点B（m,n），则tan∠POB，得m=9n，又点B在函数 的图象上，得，所以m=3（－3舍去），点B为，‎ 而AB∥x轴，所以点A（，），所以；‎ ‎（2）由条件可知所求抛物线开口向下，设点A（a , a），B（，a），则AB=－ a = ,‎ 所以，解得 .‎ 当a = －3时，点A（―3，―3），B（―，―3），因为顶点在y = x上，所以顶点为（－，－），所以可设二次函数为，点A代入，解得k= －,所以所求函数解析式为 .‎ 同理，当a = 时，所求函数解析式为；‎ ‎（3）设A（a , a），B（，a），由条件可知抛物线的对称轴为 .‎ 设所求二次函数解析式为： .‎ 点A（a , a）代入，解得，，所以点P到直线AB的距离为3或。‎ ‎【038】解：（1）矩形（长方形）；．‎ ‎（2）①，，．‎ ‎，即，，． 4分 同理，，即，‎ ‎，．． 6分 ‎②在和中，‎ ‎[来源:学科网ZXXK]． 7分 ‎．设，[来源:学科网]在中， ，解得． 8分 ‎． 9分 ‎（3）存在这样的点和点，使． 10分 Q C B A O x P y H 点的坐标是，． 12分 对于第（3）题，我们提供如下详细解答，对学生无此要求．‎ 过点画于，连结，则，‎ ‎，，‎ ‎．设，，Q C B A O x P y H ，‎ 如图1，当点P在点B左侧时， ‎ ‎，‎ 在中，，[来源:学科网ZXXK]‎ 解得，（不符实际，舍去）．‎ ‎，．‎ ‎②如图2，当点P在点B右侧时，，．‎ 在中，，解得．，‎ ‎．综上可知，存在点，，使．‎ ‎【039】(1) 将点A(-4，8)的坐标代入，解得． ……1分 将点B(2，n)的坐标代入，求得点B的坐标为(2，2)，‎ 则点B关于x轴对称点P的坐标为(2，-2)． 　……1分 ‎(第24题(1))‎ ‎4‎ x ‎2‎ ‎2‎ A ‎8‎ ‎-2‎ O ‎-2‎ ‎-4‎ y ‎6‎ B C D ‎-4‎ ‎4‎ Q P 直线AP的解析式是． 　……1分 令y=0，得．即所求点Q的坐标是(，0)． 　……1分 ‎(2)①　解法1：CQ=︱-2-︱=， 　……1分 故将抛物线向左平移个单位时，A′C+CB′最短，‎ 此时抛物线的函数解析式为． ……1分 ‎(第24题(2)①)‎ ‎4‎ x ‎2‎ ‎2‎ A′‎ ‎8‎ ‎-2‎ O ‎-2‎ ‎-4‎ y ‎6‎ B′‎ C D ‎-4‎ ‎4‎ A′′‎ 解法2：设将抛物线向左平移m个单位，则平移后A′，B′的坐标分别为A′(-4-m，8)和B′(2-m，2)，点A′关于x轴对称点的坐标为A′′(-4-m，-8)．‎ 直线A′′B′的解析式为． 要使A′C+CB′最短，点C应在直线A′′B′上，将点C(-2，0)代入直线A′′B′的解析式，解得．‎ 故将抛物线向左平移个单位时A′C+CB′最短，此时抛物线的函数解析式为． ……1分 ‎(第24题(2)②)‎ ‎4‎ x ‎2‎ ‎2‎ A′‎ ‎8‎ ‎-2‎ O ‎-2‎ ‎-4‎ y ‎6‎ B′‎ C D ‎-4‎ ‎4‎ A′′‎ B′′‎ ‎②　左右平移抛物线，因为线段A′B′和CD的长是定值，所以要使四边形A′B′CD的周长最短，只要使A′D+CB′最短； ……1分 第一种情况：如果将抛物线向右平移，显然有A′D+CB′‎ ‎>AD+CB，因此不存在某个位置，使四边形A′B′CD的周长最短．……1分 第二种情况：设抛物线向左平移了b个单位，则点A′和点B′的坐标分别为A′(-4-b，8)和B′(2-b，2)．‎ 因为CD=2，因此将点B′向左平移2个单位得B′′(-b，2)，‎ 要使A′D+CB′最短，只要使A′D+DB′′最短． 　……1分 点A′关于x轴对称点的坐标为A′′(-4-b，-8)，直线A′′B′′的解析式为．要使A′D+DB′′最短，点D应在直线A′′B′′上，将点D(-4，0)代入直线A′′B′′的解析式，解得．故将抛物线向左平移时，存在某个位置，使四边形A′B′CD的周长最短，此时抛物线的函数解析式为．……1分 ‎【040】（1）解 ①如图1，当在△ABC内时，重叠部分是平行四边形,由题意得：‎ ‎ 解得x=……（2分）‎ ‎ ②如图3，当在△ABC内时，重叠部分是平行四边形,由题意得： ‎ ‎ N= 列式得()×=‎ 解得x=……（2分）‎ 综上所述，当△与△重叠部分面积 为平方厘米时，△移动的时间为或（）秒。‎ 图1‎ 图2‎ 图3‎ 图1‎ ‎（2） ①如图1，当0≤x≤时 ……（1分）‎ ‎②如图2，当≤x≤时，如图，△DN, △,△是等腰直角三角形， N＝，GF=MN=,‎ 即…(3分)‎ ‎③如图3，当≤x≤时，…（1分）‎ ‎（3）①当0≤x≤时， ……（1分）‎ ‎②当≤x≤时， ……（2分）‎ ‎③当≤x≤时， ……（1分）‎ 所以，△与△重叠部分面积的最大值为5。‎ ‎【041】（1）如图 （3分）‎ y（千米）‎ x（小时）‎ ‎150‎ ‎100‎ ‎50‎ ‎-1‎ ‎1‎ ‎0‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ A C B D E ‎（2）2次 （5分）‎ ‎（3）如图，设直线的解析式为，‎ 图象过，‎ ‎．① （7分）‎ 设直线的解析式为，‎ 图象过，‎ ‎．② （7分）‎ 解由①、②组成的方程组得 最后一次相遇时距离乌鲁木齐市的距离为112.5千米． （12分）‎ ‎【042】解：（1）∵点是的中点，∴，∴．‎ 又∵是的角平分线，∴，‎ ‎∴，∴． 3分 ‎（2）过点作的平分线的垂线，垂足为，点即为所求．‎ y O x D B P E F M 易知点的坐标为（2，2），故，作，‎ ‎∵是等腰直角三角形，∴，‎ ‎∴点的坐标为（3，3）．‎ ‎∵抛物线经过原点，∴设抛物线的解析式为．‎ 又∵抛物线经过点和点，∴有 解得 ‎∴抛物线的解析式为． 7分 ‎（3）由等腰直角三角形的对称性知D点关于的平分线的对称点即为点．‎ 连接，它与的平分线的交点即为所求的点（因为，而两点之间线段最短），此时的周长最小．‎ ‎∵抛物线的顶点的坐标，点的坐标，‎ 设所在直线的解析式为，则有，解得．‎ ‎∴所在直线的解析式为．‎ 点满足，解得，故点的坐标为．‎ 的周长即是．‎ ‎（4）存在点，使．其坐标是或． 14分 ‎【043】解（Ⅰ），‎ ‎. 1分 将分别代入，得 ‎，‎ 解得.函数的解析式为． 3分 ‎（Ⅱ）由已知，得，设的高为，‎ ‎，即.‎ 根据题意，，由，得.‎ 当时，解得；‎ 当时，解得.‎ 的值为. 6分 ‎（Ⅲ）由已知，得.‎ ‎，，‎ ‎，化简得.‎ ‎，得，　　　　　　.‎ 有.‎ 又，，，‎ 当时，；当时，；‎ 当时，. 10分 ‎ ‎【044】(1) 配方,得y=(x–2)2 –1，∴抛物线的对称轴为直线x=2，顶点为P(2，–1) ．‎ 取x=0代入y=x2 –2x＋1，得y=1，∴点A的坐标是(0，1)．由抛物线的对称性知，点A(0，1)与点B关于直线x=2对称，∴点B的坐标是(4，1)． 2分 设直线l的解析式为y=kx＋b(k≠0)，将B、P的坐标代入，有 解得∴直线l的解析式为y=x–3．3分 ‎(2) 连结AD交O′C于点E，∵ 点D由点A沿O′C翻折后得到，∴ O′C垂直平分AD．[来源:Z。xx。k.Com]‎ 由(1)知，点C的坐标为(0，–3)，∴ 在Rt△AO′C中，O′A=2，AC=4，∴ O′C=2．‎ 据面积关系，有 ×O′C×AE=×O′A×CA，∴ AE=，AD=2AE=．‎ 作DF⊥AB于F，易证Rt△ADF∽Rt△CO′A，∴，‎ ‎∴ AF=·AC=，DF=·O′A=，5分 又 ∵OA=1，∴点D的纵坐标为1–= –，‎ ‎∴ 点D的坐标为(，–)．‎ ‎(3) 显然，O′P∥AC，且O′为AB的中点，‎ ‎∴ 点P是线段BC的中点，∴ S△DPC= S△DPB ．‎ 故要使S△DQC= S△DPB，只需S△DQC=S△DPC ．‎ ‎ 过P作直线m与CD平行，则直线m上的任意一点与CD构成的三角形的面积都等于S△DPC ，故m与抛物线的交点即符合条件的Q点．‎ 容易求得过点C(0，–3)、D(，–)的直线的解析式为y=x–3，‎ 据直线m的作法，可以求得直线m的解析式为y=x–．[来源:学_科_网]‎ 令x2–2x＋1=x–，解得 x1=2，x2=，代入y=x–，得y1= –1，y2=，‎ 因此，抛物线上存在两点Q1(2，–1)(即点P)和Q2(，)，使得S△DQC= S△DPB． ‎ ‎【045】（1）将A（0，1）、B（1，0）坐标代入得解得 ‎∴抛物线的解折式为…（2分）‎ ‎（2）设点E的横坐标为m，则它的纵坐标为 ‎ 即 E点的坐标（，）又∵点E在直线上[来源:Z§xx§k.Com]‎ ‎∴ 解得（舍去），‎ ‎∴E的坐标为（4，3）……（4分）‎ ‎（Ⅰ）当A为直角顶点时 过A作AP1⊥DE交x轴于P1点，设P1（a,0） 易知D点坐标为（－2，0） 由Rt△AOD∽Rt△POA得 即，∴a＝ ∴P1（，0）……（5分）‎ ‎（Ⅱ）同理，当E为直角顶点时，P2点坐标为（，0）……（6分）‎ ‎（Ⅲ）当P为直角顶点时，过E作EF⊥x轴于F，设P3（、）由∠OPA+∠FPE＝90°，得∠OPA＝∠FEP Rt△AOP∽Rt△PFE ‎ 由得 解得，‎ ‎∴此时的点P3的坐标为（1，0）或（3，0）……（8分）‎ 综上所述，满足条件的点P的坐标为（，0）或（1，0）或（3，0）或（‎ ‎，0）[来源:学科网]（Ⅲ）抛物线的对称轴为…（9分）∵B、C关于x＝对称 ∴MC＝MB 要使最大，即是使最大 ‎ 由三角形两边之差小于第三边得，当A、B、M在同一直线上时的值最大．易知直线AB的解折式为∴由 得 ‎ ∴M（，－）……（11分）‎ ‎【046】网]（1）解：由得点坐标为 由得点坐标为∴ （2分）‎ 由解得∴点的坐标为 （3分）‎ ‎∴ （4分）‎ ‎ （2）解：∵点在上且 ‎∴点坐标为（5分）又∵点在上且 ‎∴点坐标为（6分）∴（7分）‎ ‎（3）解法一：当时，如图1，矩形与重叠部分为五边形（时，为四边形）．过作于，则 A D B E O R F x y y M ‎（图3）‎ G C A D B E O C F x y y G ‎（图1）‎ R M A D B E O C F x y y G ‎（图2）‎ R M ‎∴即∴‎ ‎∴‎ 即 ‎【047】解：方法一：如图（1-1），连接．‎ N 图（1-1）‎ A B C D E F M ‎ 由题设，得四边形和四边形关于直线对称．‎ ‎ ∴垂直平分．∴ 1分 ‎ ∵四边形是正方形，∴‎ ‎ ∵设则 在中，．∴解得，即 3分 ‎ 在和在中，，，‎ ‎ 5分 ‎ 设则∴‎ ‎ 解得即 ∴ 7分 ‎ 方法二：同方法一， 3分 ‎ 如图（1－2），过点做交于点，连接 N 图（1-2）‎ A B C D E F M G ‎　　　‎ ‎∵∴四边形是平行四边形．‎ ‎ ∴‎ ‎ 同理，四边形也是平行四边形．∴‎ ‎　　　∵‎ ‎　　　‎ ‎　　　在与中 ‎　　　∴ ５分 ‎∵∴ 7分 类比归纳 ‎（或）；； 12分 ‎【048】解：（1）由题意得 6=a(－2＋3)(－2－1)，∴a=－2，‎ ‎∴抛物线的函数解析式为y=－2(x＋3)(x－1)与x轴交于B（－3，0）、A（1，0）‎ 设直线AC为y=kx＋b，则有0=k＋b，6=－2k＋b，解得 k=－2，b=2，‎ ‎∴直线AC为y=－2x＋2‎ ‎（2）①设P的横坐标为a(－2≤a≤1)，则P（a，－‎2a＋2），M（a，－‎2a2－‎4a＋6）‎ ‎∴PM=－‎2a2－‎4a＋6－(－‎2a＋2)=－‎2a2－‎2a＋4=－‎2a2＋a＋14＋92‎ ‎=‎-2a+122+92，∴当a=-12时，PM的最大值为926分 ‎②M1（0，6）M2-14，678 ‎ ‎【049】解：（1）由题意得 解得 ‎∴此抛物线的解析式为 3分 ‎（2）连结、.因为的长度一定，所以周长最小，就是使最小.点关于对称轴的对称点是点，与对称轴的交点即为所求的点.‎ ‎（第24题图）‎ O A C x y B E P D 设直线的表达式为则解得 ‎∴此直线的表达式为 把代入得∴点的坐标为 ‎（3）存在最大值，理由：∵即 ‎∴∴即 ‎∴‎ 方法一：连结，‎ ‎=[来源:Z。xx。k.Com]‎ ‎=，∵∴当时， 9分 方法二：‎ ‎=‎ ‎=，∵∴当时， 9分 ‎【050】解：（1）∵A E D Q P B F C N M ∴．而，‎ ‎∴，∴．∴当．‎ ‎（2）∵平行且等于，[来源:学科网]‎ ‎∴四边形是平行四边形．‎ ‎∴．‎ ‎∵，∴．∴．‎ ‎∴．．∴．‎ 过B作，交于，过作，交于．‎ ‎．∵，‎ ‎∴．又，，，‎ ‎，．‎ ‎（3）．‎ 若，则有，解得．‎ ‎（4）在和中，‎ ‎∴．‎ ‎∴在运动过程中，五边形的面积不变．‎ ‎【051】解：（1），（-1，0），B（3，0）． 3分 ‎（2）如图14（1），抛物线的顶点为M（1，-4），连结OM．‎ ‎ 则 △AOC的面积=，△MOC的面积=，△MOB的面积=6，∴ 四边形 ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=9． 6分 ‎ 图14（2）‎ 说明：也可过点M作抛物线的对称轴，将四边形ABMC的面 积转化为求1个梯形与2个直角三角形面积的和．‎ ‎（3）如图14（2），设D（m，），连结OD．‎ 则 0＜m＜3， ＜0． 且 △AOC的面积=，△DOC的面积=， ‎ ‎△DOB的面积=-（），‎ ‎∴ 四边形 ABDC的面积=△AOC的面积+△DOC的面积+△DOB的面积 ‎==．‎ 图14（3） 图14（4）‎ ‎∴ 存在点D，使四边形ABDC的面积最大为． ‎ ‎（4）有两种情况：‎ 如图14（3），过点B作BQ1⊥BC，交抛物线于点Q1、交y轴于点E，连接Q‎1C．‎ ‎∵ ∠CBO=45°，∴∠EBO=45°，BO=OE=3． ‎ ‎∴ 点E的坐标为（0，3）． ∴ 直线BE的解析式为． 12分 由 解得 ∴ 点Q1的坐标为（-2，5）． 13分 如图14（4），过点C作CF⊥CB，交抛物线于点Q2、交x轴于点F，连接BQ2．‎ ‎∵ ∠CBO=45°，∴∠CFB=45°，OF=OC=3． ‎ ‎∴ 点F的坐标为（-3，0）．∴ 直线CF的解析式为． 14分 由 解得 ‎ ‎∴点Q2的坐标为（1，-4）．综上，在抛物线上存在点Q1（-2，5）、Q2（1，-4），‎ 使△BCQ1、△BCQ2是以BC为直角边的直角三角形．‎ y x O B A D C ‎(x=m)‎ ‎(F2)F1‎ E1 (E2)‎ ‎【052】解：（1）根据题意，得 解得．．（2分）‎ ‎（2）当时，得或，‎ ‎∵，当时，得，‎ ‎∴，∵点在第四象限，∴． （4分）‎ 当时，得，∴，‎ ‎∵点在第四象限，∴． （6分）‎ ‎（3）假设抛物线上存在一点，使得四边形为平行四边形，则 ‎，点的横坐标为，‎ 当点的坐标为时，点的坐标为，‎ ‎∵点在抛物线的图象上，∴，∴，‎ ‎∴，∴（舍去），∴，‎ ‎∴． （9分）‎ 当点的坐标为时，点的坐标为，‎ ‎∵点在抛物线的图象上，∴，∴，‎ ‎∴，∴（舍去），，∴，∴．‎ ‎【053】解：（1）设，把代入，得， 2分 ‎∴抛物线的解析式为：．顶点的坐标为． 5分 ‎（2）设直线解析式为：（），把两点坐标代入，‎ 得解得．∴直线解析式为． 7分 ‎，∴ 9分 ‎ ． 10分 ‎∴当时，取得最大值，最大值为． 11分 ‎(E)‎ ‎1‎ ‎2‎ ‎3‎ ‎3‎ ‎1‎ D y C B A P ‎2‎ x O F M H ‎（3）当取得最大值，，，∴．∴四边形是矩形．‎ 作点关于直线的对称点，连接．‎ 法一：过作轴于，交轴于点．‎ 设，则．‎ 在中，由勾股定理，．‎ 解得．∵，∴．‎ 由，可得，．∴．‎ ‎∴坐标． 13分 法二：连接，交于点，分别过点作的垂线，垂足为．‎ 易证．‎(E)‎ ‎1‎ ‎2‎ ‎3‎ ‎3‎ ‎1‎ D y C B A P ‎2‎ x O F M H N M ∴．‎ 设，则．∴，．‎ 由三角形中位线定理，．‎ ‎∴，即．‎ ‎∴坐标． 13分 把坐标代入抛物线解析式，不成立，所以不在抛物线上． 14分 ‎【054】（1）由抛物线经过点A(0，1)，C(2，4)，‎ 得解得 ‎∴抛物线对应的函数关系式为：． （2分）‎ ‎（2）当时，P点坐标为(1，1)，∴Q点坐标为(2，0)． ‎ ‎ 当时，P点坐标为(2，3)，∴Q点坐标为(5，0)． （5分）‎ ‎（3）当≤2时，．S． ‎ ‎ 当≤5时，．S． （8分）‎ B A D C O M N x y P1‎ P2‎ ‎ 当时，S的最大值为2． （10分）‎ ‎【055】（1）过点作轴，垂足为，‎ ‎；‎ 又，‎ ‎，‎ 点的坐标为； 4分 ‎（2）抛物线经过点，则得到， 5分 解得，所以抛物线的解析式为； 7分 ‎（3）假设存在点，使得仍然是以为直角边的等腰直角三角形：‎ 若以点为直角顶点；‎ 则延长至点，使得，得到等腰直角三角形， 8分 过点作轴，；‎ ‎，可求得点； 11分 若以点为直角顶点；‎ 则过点作，且使得，得到等腰直角三角形， 12分 过点作轴，同理可证； 13分 ‎，可求得点； 14分 经检验，点与点都在抛物线上． 16分 ‎【056】解：（1） C（3，0）；‎ ‎（2）①抛物线，令=0，则=， ∴A点坐标（0，c）．‎ ‎∵，∴ ，∴点P的坐标为（）． ‎ ‎∵PD⊥轴于D，∴点D的坐标为（）． ……………………………………5分 根据题意，得a=a′，c= c′，∴抛物线F′的解析式为．‎ 又∵抛物线F′经过点D（），∴．……………6分 ‎∴．又∵，∴．∴b:b′=．‎ ‎②由①得，抛物线F′为．‎ 令y=0，则． ∴．‎ ‎∵点D的横坐标为∴点C的坐标为（）．‎ 设直线OP的解析式为．∵点P的坐标为（），‎ ‎∴，∴，∴．‎ ‎∵点B是抛物线F与直线OP的交点，∴．∴．‎ ‎∵点P的横坐标为，∴点B的横坐标为．‎ 把代入，得．‎ ‎∴点B的坐标为．∴BC∥OA，AB∥OC．（或BC∥OA，BC =OA），‎ ‎∴四边形OABC是平行四边形．‎ 又∵∠AOC=90°，∴四边形OABC是矩形． ‎ ‎【057】(1) ‎ ‎ (2)∵，，∴‎ 当点 在上运动时，，‎ ‎；‎ 当点 在上运动时，作于点，‎ 有∵，∴‎ ‎∴‎ ‎（3）当时，，，‎ 此时，过各顶点作对边的平行线，与坐标轴无第二个交点，所以点不存在； ‎ 当时，，，此时，、‎ ‎【058】解：（1）令，得 解得，令，得 E C B y P A ‎∴ A B C 3分 ‎（2）∵OA=OB=OC= ∴BAC=ACO=BCO=‎ ‎∵AP∥CB，∴PAB=，过点P作PE轴于E，‎ 则APE为等腰直角三角形 令OE=，则PE= ∴P ‎∵点P在抛物线上 ∴ ‎ 解得，（不合题意，舍去） ∴PE= 4分 ‎∴四边形ACBP的面积=AB•OC+AB•PE= 5分 ‎(3)． 假设存在∵PAB=BAC = ∴PAAC ‎∵MG轴于点G， ∴MGA=PAC =‎ 在Rt△AOC中，OA=OC= ∴AC=，在Rt△PAE中，AE=PE= ∴AP= 6分 ‎ G M C B y P A 设M点的横坐标为，则M ‎ ‎①点M在轴左侧时，则 ‎(ⅰ) 当AMG PCA时，有=∵AG=，‎ MG=即 解得（舍去） ‎ ‎（舍去）………7分 ‎(ⅱ) 当MAG PCA时有=‎ G M C B y P A 即 ，解得：（舍去） ‎ ‎ ∴M 8分 ‎② 点M在轴右侧时，则 ‎ ‎(ⅰ) 当AMG PCA时有=‎ ‎∵AG=，MG= ‎ ‎∴ 解得（舍去） ∴M ‎ ‎(ⅱ) 当MAGPCA时有= 即 ‎ 解得：（舍去） ∴M ∴存在点M，使以A、M、G三点为顶点的三角形与PCA相似，M点的坐标为，， ‎ M B E A C N D F G 图（1）‎ H ‎【059】解：（1）∵四边形ABCD和四边形AEFG是正方形 ‎ ∴AB=AD，AE=AG，∠BAD＝∠EAG＝90º ‎∴∠BAE＋∠EAD＝∠DAG＋∠EAD ‎∴∠BAE＝∠DAG ‎∴△ BAE≌△DAG …………4分 ‎（2）∠FCN＝45º …………5分 理由是：作FH⊥MN于H ‎ ‎ ∵∠AEF＝∠ABE＝90º ‎ ∴∠BAE +∠AEB＝90º，∠FEH+∠AEB＝90º ‎ ∴∠FEH＝∠BAE 又∵AE=EF，∠EHF＝∠EBA＝90º ‎∴△EFH≌△ABE …………7分 ‎∴FH＝BE，EH＝AB＝BC，∴CH＝BE＝FH ‎∵∠FHC＝90º，∴∠FCH＝45º …………8分 M B E A C N D F G 图（2）‎ H ‎（3）当点E由B向C运动时，∠FCN的大小总保持不变，…………9分 理由是：作FH⊥MN于H ‎ 由已知可得∠EAG＝∠BAD＝∠AEF＝90º 结合（1）（2）得∠FEH＝∠BAE＝∠DAG 又∵G在射线CD上，∠GDA＝∠EHF＝∠EBA＝90º ‎ ∴△EFH≌△GAD，△EFH∽△ABE ……11分 ‎∴EH＝AD＝BC＝b，∴CH＝BE，∴＝＝ ‎∴在Rt△FEH中，tan∠FCN＝＝＝ ‎ B A O C y x 第26题图 Q4‎ Q3‎ Q1‎ Q2‎ P3‎ P1‎ P2‎ D C P4‎ ‎∴当点E由B向C运动时，∠FCN的大小总保持不变，tan∠FCN＝ ‎【060】解：（1）根据题意，得 ‎，解得 抛物线的解析式为，顶点坐标是（2，4）‎ ‎（2），设直线的解析式为 直线经过点点 ‎ ‎（3）存在．，，，‎ ‎【061】解（1）A（，0），B（0，3） 2分（每对一个给1分）‎ ‎（2）满分3分．其中过F作出垂线1分，作出BF中垂线1分，找出圆心并画出⊙P给1分． （注：画垂线PF不用尺规作图的不扣分）‎ ‎（3）过点P作PD⊥轴于D，则PD=，BD=， 6分 y x O A B D P F PB=PF=，∵△BDP为直角三形，∴ ‎ ‎∴，即 即∴与的函数关系为 ‎（4）存在 解法1：∵⊙P与轴相切于点F，且与直线相切于点B ‎∴，∵，∴‎ ‎∵AF= ， ∴，∴ 11分 把代入，得 ‎∴点P的坐标为（1，）或（9，15）12分 ‎【062】解：实践应用（1）2；．；．（2）．‎ 拓展联想（1）∵△ABC的周长为l，∴⊙O在三边上自转了周． ‎ 又∵三角形的外角和是360°，‎ ‎∴在三个顶点处，⊙O自转了（周）． ‎ ‎∴⊙O共自转了（+1）周． ‎ ‎（2）+1．‎ ‎【063】（1）① 对称轴 （2分）‎ ‎② 当时，有，解之，得 ，‎ ‎∴ 点A的坐标为（，0）． （4分）‎ ‎（2）满足条件的点P有3个，分别为（，3），（2，3），（，）． （7分）‎ ‎（3）存在．当时， ∴ 点C的坐标为（0，3）‎ ‎∵ DE∥轴，AO3，EO2，AE1，CO3‎ ‎∴ ∽ ∴ 即 ∴ DE1 （9分）‎ ‎∴ 4‎ 在OE上找点F，使OF，此时2，直线CF把四边形DEOC 分成面积相等的两部分，交抛物线于点M． （10分）‎ 设直线CM的解析式为，它经过点．则 （11分）‎ 解之，得 ∴ 直线CM的解析式为 （12分）‎ B O A ‎·‎ x y 第28题图 P H ‎【064】解：（1）抛物线与y轴的交于点B，令x=0得y=2．‎ ‎∴B（0，2） ‎ ‎∵ ∴A（—2，3）‎ ‎（2）当点P是 AB的延长线与x轴交点时，‎ ‎．‎ 当点P在x轴上又异于AB的延长线与x轴的交点时，‎ 在点P、A、B构成的三角形中，．‎ 综合上述： ‎ ‎（3）作直线AB交x轴于点P，由（2）可知：当PA—PB最大时，点P是所求的点 8分 作AH⊥OP于H．∵BO⊥OP，∴△BOP∽△AHP ‎ ∴ 由（1）可知：AH=3、OH=2、OB=2，∴OP=4，故P（4，0） ‎ ‎【065】解：（1）∵AB是⊙O的直径（已知）‎ ‎ ∴∠ACB＝90º（直径所对的圆周角是直角）‎ ‎ ∵∠ABC＝60º（已知）‎ ‎ ∴∠BAC＝180º－∠ACB－∠ABC＝ 30º（三角形的内角和等于180º）‎ ‎ ∴AB＝2BC＝‎4cm（直角三角形中，30º锐角所对的直角边等于斜边的一半）‎ ‎ 即⊙O的直径为‎4cm．‎ ‎（2）如图10（1）CD切⊙O于点C，连结OC，则OC＝OB＝1/2·AB＝‎2cm．‎ ‎∴CD⊥CO（圆的切线垂直于经过切点的半径）‎ ‎∴∠OCD＝90º（垂直的定义） ∵∠BAC＝ 30º（已求）‎ ‎∴∠COD＝2∠BAC＝ 60º ∴∠D＝180º－∠COD－∠OCD＝ 30º∴OD＝2OC＝‎4cm ∴BD＝OD－OB＝4－2＝2（cm）‎ ‎ ∴当BD长为‎2cm，CD与⊙O相切．‎ ‎（3）根据题意得：‎ BE＝（4－2t）cm，BF＝tcm；‎ 如图10（2）当EF⊥BC时，△BEF为直角三角形，此时△BEF∽△BAC ‎∴BE：BA＝BF：BC即：（4－2t）：4＝t：2解得：t＝1‎ 如图10（3）当EF⊥BA时，△BEF为直角三角形，此时△BEF∽△BCA ‎∴BE：BC＝BF：BA即：（4－2t）：2＝t：4解得：t＝1.6‎ ‎∴当t＝1s或t＝1.6s时，△BEF为直角三角形．‎ ‎【066】（1）由得，代入反比例函数中，得 ‎∴反比例函数解析式为： 2分 解方程组由化简得：‎ ‎，所以 5分 ‎ （2）无论点在之间怎样滑动，与总能相似．因为两点纵坐标相等，所以轴．‎ 又因为轴，所以为直角三角形．‎ 同时也是直角三角形，‎ ‎ 8分 ‎（在理由中只要能说出轴，即可得分．）‎ ‎【067】（1）解：∵直角梯形 O A P D B Q C 当时，四边形 为平行四边形．‎ 由题意可知：‎ 当时，四边形为平行四边形． 3分 O A P D B Q C H E ‎（2）解：设与相切于点 过点作垂足为 直角梯形 由题意可知：‎ 为的直径，‎ 为的切线 ‎ 5分 在中，，‎ 即：，，‎ ‎，因为在边运动的时间为秒 而，（舍去），当秒时，与相切． 8分 ‎【068】解：（1）如图4，过B作 则 过Q作 则 ‎ （2分）‎ 要使四边形PABQ是等腰梯形，则，‎ 即 或（此时是平行四边形，不合题意，舍去） （3分）‎ ‎（2）当时，。‎ ‎ （4分）‎ ‎ （5分）‎ ‎ （6分）‎ ‎（3）①当时，则 ‎ （7分）‎ ‎②当时，‎ 即 （8分）‎ ‎③当时， （9分）‎ 综上，当时，△PQF是等腰三角形． （10分）‎ ‎【069】解 （1）易求得点的坐标为 由题设可知是方程即 的两根，‎ 所以，所 （1分）‎ 如图3，∵⊙P与轴的另一个交点为D，由于AB、CD是⊙P的两条相交弦，设它们的交点为点O，连结DB，∴△AOC∽△DOC，则 （2分）‎ 由题意知点在轴的负半轴上，从而点D在轴的正半轴上，‎ 所以点D的坐标为（0，1） （3分）‎ ‎（2）因为AB⊥CD， AB又恰好为⊙P的直径，则C、D关于点O对称，‎ 所以点的坐标为，即 （4分）‎ 又，‎ 所以解得 （6分）‎ ‎【070】解：（1）6．（2）8． （3分）‎ ‎（3）①当0时，‎ Q1‎ A B C D Q2‎ P3‎ Q3‎ E P2‎ P1‎ O ‎． （5分）‎ ‎②当3时，‎ ‎= （7分）‎ ‎③当时，设与交于点．‎ ‎(解法一)‎ 过作则为等边三角形．‎ ‎．‎ ‎． （10分）‎ ‎（解法二）‎ 如右图，过点作于点，，于点 过点作交延长线于点．‎ P3‎ O A B C D Q3‎ G H F 又 又 ‎ （10分）‎ ‎【071】解：（1）由题意得，解得 ‎∴此抛物线的解析式为 3分 ‎（2）连结、.因为的长度一定，所以周长最小，就是使最小.点关于对称轴的对称点是点，与对称轴的交点即为所求的点.‎ ‎（第24题图）‎ O A C x y B E P D 设直线的表达式为 则 解得 ‎∴此直线的表达式为……5分 把代入得∴点的坐标为 6分 ‎（3）存在最大值 7分 理由：∵即 ‎∴∴即 ‎∴‎ 方法一：‎ 连结 ‎=‎ ‎= 8分 ‎∵，∴当时， 9分 方法二：‎ ‎ =‎ ‎= 8分 ‎∵，∴当时， 9分 ‎【072】解：（1）①，，，S梯形OABC=12 ‎ ‎②当时，直角梯形OABC被直线扫过的面积=直角梯形OABC面积－直角三角开DOE面积 ‎ ‎（2） 存在 ， ‎ 对于第（2）题我们提供如下详细解答（评分无此要求）.下面提供参考解法二：‎ ‎ 以点D为直角顶点，作轴 ‎ ‎ 设.（图示阴影），在上面二图中分别可得到点的生标为P（－12，4）、P（－4，4）E点在0点与A点之间不可能；‎ ‎② 以点E为直角顶点 ‎ ‎ 同理在②二图中分别可得点的生标为P（－，4）、P（8，4）E点在0点下方不可能.‎ 以点P为直角顶点 同理在③二图中分别可得点的生标为P（－4，4）（与①情形二重合舍去）、P（4，4），‎ E点在A点下方不可能.‎ 综上可得点的生标共5个解，分别为P（－12，4）、P（－4，4）、P（－，4）、‎ P（8，4）、P（4，4）．‎ 下面提供参考解法二：‎ 以直角进行分类进行讨论（分三类）：‎ 第一类如上解法⑴中所示图 ‎，直线的中垂线方程：，令得．由已知可得即化简得解得 ；‎ 第二类如上解法②中所示图 ‎，直线的方程：，令得．由已知可得即化简得解之得 ，‎ 第三类如上解法③中所示图 ‎，直线的方程：，令得．由已知可得即 解得 ‎（与重合舍去）．‎ 综上可得点的生标共5个解，分别为P（－12，4）、P（－4，4）、P（－，4）、‎ P（8，4）、P（4，4）．‎ 事实上，我们可以得到更一般的结论：‎ 如果得出设，则P点的情形如下 直角分类情形 ‎【073】(1)∵∠A、∠C所对的圆弧相同，∴∠A＝∠C．‎ ‎∴Rt△APD∽Rt△CPB，∴，∴PA·PB＝PC·PD；………………………3分 ‎(2)∵F为BC的中点，△BPC为Rt△，∴FP＝FC，∴∠C＝∠CPF．‎ 又∠C＝∠A，∠DPE＝∠CPF，∴∠A＝∠DPE．∵∠A＋∠D＝90°，‎ ‎∴∠DPE＋∠D＝90°．∴EF⊥AD．‎ ‎(3)作OM⊥AB于M，ON⊥CD于N，同垂径定理：‎ O y x C D B A D1‎ O1‎ O2‎ O3‎ P ‎60°‎ ‎（第22题答图）‎ l ‎∴OM2＝(2)2－42＝4，ON2＝(2)2－32＝11‎ 又易证四边形MONP是矩形，‎ ‎∴OP＝ ‎ ‎【074】（1）解：由题意得，‎ 点坐标为．在中，，‎ 点的坐标为． ‎ 设直线的解析式为，由过两点，得 解得直线的解析式为：．‎ ‎（2）如图，设平移秒后到处与第一次外切于点，‎ 与轴相切于点，连接．则 轴，，‎ 在中，． 6分 ‎，，‎ ‎（秒）平移的时间为5秒． 8分 ‎【075】解：（1）对称轴是直线：，‎ 点A的坐标是（3，0）． 2分 ‎（说明：每写对1个给1分，“直线”两字没写不扣分）‎ ‎（2）如图11，连接AC、AD，过D作于点M，‎ 解法一：利用 ‎∵点A、D、C的坐标分别是A （3，0），D（1，）、C（0，），‎ ‎∴AO＝3，MD=1．由得∴ 3分 又∵∴由 得 ‎ ‎∴函数解析式为： 6分 解法二：利用以AD为直径的圆经过点C ‎∵点A、D的坐标分别是A （3，0） 、D（1，）、C（0，），‎ ‎∴，，∵‎ ‎∴…① 又∵…② 4分 由①、②得 ∴函数解析式为： 6分 ‎（3）如图所示，当BAFE为平行四边形时，则∥，并且＝．‎ ‎ ∵=4，∴=4 ，由于对称为，∴点F的横坐标为5． 7分 y x O A B C D 图11‎ E F 将代入得，∴F（5，12）． ‎ 根据抛物线的对称性可知，在对称轴的左侧 抛物线上也存在点F，使得四边形BAEF是 平行四边形，此时点F坐标为（，12）． ‎ 当四边形BEAF是平行四边形时，‎ 点F即为点D，此时点F的坐标为（1，）． ‎ 综上所述，点F的坐标为（5，12），‎ ‎（，12）或（1，）．‎ ‎【076】解：（1）∵四边形OBHC为矩形，∴CD∥AB，‎ ‎ 又D（5，2）， ∴C（0，2），OC=2 . ‎ ‎ ∴ 解得 ‎ ∴抛物线的解析式为： …… 4分 ‎（2）点E落在抛物线上. 理由如下：……… 5分 由y = 0，得. 解得x1=1，x2=4. ∴A（4，0），B（1，0）. ‎ ‎ ∴OA=4，OB=1. 由矩形性质知：CH=OB=1，BH=OC=2，∠BHC=90°，‎ 由旋转、轴对称性质知：EF=1，BF=2，∠EFB=90°，∴点E的坐标为（3，－1）. ‎ 把x=3代入，得， ∴点E在抛物线上. ‎ ‎（3）法一：存在点P（a，0），延长EF交CD于点G，易求OF=CG=3，PB=a－1.‎ ‎ S梯形BCGF = 5，S梯形ADGF = 3，记S梯形BCQP = S1，S梯形ADQP = S2，‎ ‎ 下面分两种情形： ①当S1∶S2 =1∶3时，，‎ 此时点P在点F（3，0）的左侧，则PF = 3－a，由△EPF∽△EQG，得 ‎，则QG=9－‎3a，∴CQ=3－(9－‎3a) =‎3a －6，由S1=2，得，解得； ‎ ‎②当S1∶S2=3∶1时，，此时点P在点F（3，0）的右侧，则PF = a－3，由△EPF∽△EQG，得QG = ‎3a－9，∴CQ = 3 +（‎3 a－9）= ‎3 a－6，‎ 由S1= 6，得，解得，综上所述：所求点P的坐标为（，0）或（，0）……… 14分 ‎ 法二：存在点P（a，0）. 记S梯形BCQP = S1，S梯形ADQP = S2，易求S梯形ABCD = 8.‎ 当PQ经过点F（3，0）时，易求S1=5，S2 = 3，此时S1∶S2不符合条件，故a≠3.‎ 设直线PQ的解析式为y = kx+b(k≠0)，则，解得，‎ ‎∴. 由y = 2得x = ‎3a－6，∴Q（‎3a－6，2） ……… 10分 ‎∴CQ = ‎3a－6，BP = a－1，.‎ 下面分两种情形：①当S1∶S2 = 1∶3时，= 2；‎ ‎∴‎4a－7 = 2，解得；……………………………………………… 12分 ‎②当S1∶S2 = 3∶1时，； ∴‎4a－7 = 6，解得；‎ 综上所述：所求点P的坐标为（，0）或（，0）………… 14分 ‎[说明：对于第（3）小题，只要考生能求出或两个答案，就给6分. ]‎ ‎【077】解：（1）把B（0，6）代入，得＝6………………………1分 ‎ 把＝0代入，得＝8‎ ‎∴点A的坐标为（8，0）…………… 3分 ‎（2）在矩形OACB中，AC＝OB＝6，‎ BC＝OA＝8，∠C＝90°‎ ‎∴AB＝‎ ‎∵PD⊥AB∴∠PDB=∠C＝90°‎ ‎，∴∴∴‎ 又∵BC∥AE，∴△PBD∽△EAD ‎∴，即，∴‎ ‎∵，∴ （）……………………………7分 （注：写成不扣分）‎ ‎② ⊙Q是△OAB的内切圆 ，可设⊙Q的半径为r ‎∵,解得r=2.………………………………………8分 设⊙Q与OB、AB、OA分别切于点F、G、H 可知，OF＝2∴BF＝BG＝OB－OF＝6－2＝4，设直线PD与⊙Q交于点 I、J ，过Q作QM⊥IJ于点M，连结IQ、QG， ∵QI＝2， ‎ ‎ ∴ ∴ 在矩形GQMD中，GD＝QM＝1.6‎ ‎∴BD＝BG+GD＝4+1.6＝5.6，由，得 ‎∴点P的坐标为（7，6）…………………………………………………………………11分 当PE在圆心Q的另一侧时，同理可求点P的坐标为（3，6）………………………12分 综上，P点的坐标为（7，6）或（3，6）．………………………………………………13分。‎ ‎【078】（1） 2分 ‎（2）∵，∴点的横坐标为，‎ ‎①当，即时，，‎ ‎∴． 3分 ‎②当时，，‎ ‎∴．∴ 4分 当，即时，，‎ ‎∴当时，有最大值． 6分 ‎（3）由，所以是等腰直角三角形，若在上存在点，使得是以为直角顶点的等腰直角三角形，则，所以，又轴，则，两点关于直线对称，所以，得． 7 分 L A O P B x y L1‎ ‎23题图-1‎ Q C 下证．连，则四边形是正方形． ‎ 法一：（i）当点在线段上，在线段上 ‎（与不重合）时，如图–1． ‎ 由对称性，得， ‎ ‎∴ ， ‎ ‎∴ ． 8分 ‎（ii）当点在线段的延长线上，在线段上时，如图–2，如图–3 ‎ ‎∵， ∴． 9分 ‎ ‎（iii）当点与点重合时，显然． ‎ 综合（i）（ii）（iii），． ‎ y L A O P B x L1‎ ‎23题图-3‎ Q C ‎2‎ ‎1‎ ‎∴在上存在点，使得是以为直角顶点的等腰直角三角形． 11 分 ‎ L A O P B x L1‎ ‎23题图-2‎ Q C ‎2‎ ‎1‎ y 法二：由，所以是等腰直角三角形，若在上存在点，使得是以为直角顶点的等腰直角三角形，则，所以，又轴， 则，两点关于直线对称，所以，得． 7 分 ‎ 延长与交于点． ‎ ‎（i）如图–4，当点在线段上（与不重合）时，‎ ‎∵四边形是正方形， ‎ ‎∴四边形和四边形都是矩形，和都是等腰直角三角形．‎ ‎∴． ‎ L A O P B x y L1‎ ‎23题图-1‎ Q C 又∵， ∴， ‎ ‎ ∴， ‎ ‎∴， ‎ 又∵，‎ ‎∴． ‎ ‎ ∴． 8分 ‎（ii）当点与点重合时，显然． 9分 ‎ ‎（iii）在线段的延长线上时，如图–5， ‎ ‎∵，∠1=∠2 ‎ ‎ ∴ ‎ 综合（i）（ii）（iii），． ‎ ‎∴在上存在点，使得是以为直角顶点的等腰直角三角形． 11分 ‎23题图-4‎ L A O M P B x y L1‎ Q C N y L A O P B x L1‎ ‎23题图-5‎ Q C ‎2‎ ‎1‎ 法三：由，所以是等腰直角三角形，若在上存在点，使得是以为直角顶点的等腰直角三角形，则，所以，又轴， ‎ ‎ 则，O两点关于直线对称，所以，得． 9分 连，∵，，，‎ ‎∴，‎ ‎．‎ ‎∴，∴． 10分 ‎∴在上存在点，使得是以为直角顶点的等腰直角三角形． 11分 ‎【079】解：（1）解得 ‎ ， 1分 在中，由勾股定理有， ‎ ‎（2）∵点在轴上，，，‎ ‎ 1分 由已知可知D（6，4），设当时有 解得，同理时， 1分 在中，‎ 在中，，，‎ ‎（3）满足条件的点有四个， 4分 说明：本卷中所有题目，若由其它方法得出正确结论，可参照本评 C P Q B A M D N ‎【080】（1）过点作，垂足为．则，‎ 当运动到被垂直平分时，四边形是矩形，‎ 即时，四边形是矩形，‎ 秒时，四边形是矩形．‎ C P Q B A M N ‎，‎ ‎（2）当时，‎ C P Q B A M N 当时 C P Q B A M N 当时，‎ ‎ 10分 ‎【081】解：（1）（0，－3），b＝－，c＝－3． 3分 ‎（2）由（1），得y＝x2－x－3，它与x轴交于A，B两点，得B（4，0）．‎ ‎∴OB＝4，又∵OC＝3，∴BC＝5．‎ 由题意，得△BHP∽△BOC，‎ ‎∵OC∶OB∶BC＝3∶4∶5，‎ ‎∴HP∶HB∶BP＝3∶4∶5，‎ ‎∵PB＝5t，∴HB＝4t，HP＝3t．‎ ‎∴OH＝OB－HB＝4－4t．‎ 由y＝x－3与x轴交于点Q，得Q（4t，0）．‎ ‎∴OQ＝4t． 4分 ‎①当H在Q、B之间时，‎ QH＝OH－OQ ‎＝（4－4t）－4t＝4－8t． 5分 ‎②当H在O、Q之间时，‎ QH＝OQ－OH ‎＝4t－（4－4t）＝8t－4． 6分 综合①，②得QH＝｜4－8t｜； 6分 ‎（3）存在t的值，使以P、H、Q为顶点的三角形与△COQ相似． 7分 ‎①当H在Q、B之间时，QH＝4－8t，‎ 若△QHP∽△COQ，则QH∶CO＝HP∶OQ，得＝，‎ ‎∴t＝． 7分 若△PHQ∽△COQ，则PH∶CO＝HQ∶OQ，得＝，‎ 即t2＋2t－1＝0．‎ ‎∴t1＝－1，t2＝－－1（舍去）． 8分 ‎②当H在O、Q之间时，QH＝8t－4．‎ 若△QHP∽△COQ，则QH∶CO＝HP∶OQ，得＝，‎ ‎∴t＝． 9分 若△PHQ∽△COQ，则PH∶CO＝HQ∶OQ，得＝，‎ 即t2－2t＋1＝0．‎ ‎∴t1＝t2＝1（舍去）． 10分 综上所述，存在的值，t1＝－1，t2＝，t3＝． 10分 附加题：解：（1）8； 5分 ‎（2）2． 10分 ‎【082】（09上海）略 ‎【083】. 解：（1）B（1，）‎ ‎（2）设抛物线的解析式为y=ax(x+a)，代入点B（1, ），得，‎ 因此 ‎（3）如图，抛物线的对称轴是直线x=—1，当点C位于对称轴与线段AB的交点时，△BOC的周长最小.‎ C B A O y x 设直线AB为y=kx+b.所以，‎ 因此直线AB为，‎ 当x=－1时，，‎ 因此点C的坐标为（－1，）.‎ D B A O y x P ‎（4）如图，过P作y轴的平行线交AB于D.‎ ‎ ‎ 当x=－时，△PAB的面积的最大值为，此时.‎ ‎【084】解：（1）⊙P与x轴相切.‎ ‎ ∵直线y=－2x－8与x轴交于A（4，0），与y轴交于B（0，－8），‎ ‎∴OA=4，OB=8.由题意，OP=－k，∴PB=PA=8+k.‎ 在Rt△AOP中，k2+42=(8+k)2，‎ ‎∴k=－3，∴OP等于⊙P的半径，‎ ‎∴⊙P与x轴相切.‎ ‎（2）设⊙P与直线l交于C，D两点，连结PC，PD当圆心P在线段OB上时,作PE⊥CD于E.‎ ‎∵△PCD为正三角形，∴DE=CD=，PD=3，‎ ‎ ∴PE=.‎ ‎∵∠AOB=∠PEB=90°， ∠ABO=∠PBE，‎ ‎∴△AOB∽△PEB，‎ ‎∴，‎ ‎∴∴，‎ ‎∴，∴.‎ 当圆心P在线段OB延长线上时,同理可得P(0,－－8)，‎ ‎∴k=－－8，∴当k=－8或k=－－8时，以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.‎ ‎【085】解: (1)由题知: ……………………………………1 分 ‎ ‎ 解得: ……………………………………………………………2分 ‎ ‎∴ 所求抛物线解析式为: ……………………………3分 ‎ ‎ ‎(2) 存在符合条件的点P, 其坐标为P (－1, )或P(－1,－ )‎ 或P (－1, 6) 或P (－1, )………………………………………………………7分 ‎(3)解法①：‎ 过点E 作EF⊥x 轴于点F , 设E ( a ,-‎-2a＋3 )( －3< a < 0 ) ‎ ‎∴EF=-‎-2a＋3，BF=a＋3，OF=－a ………………………………………………8 分 ‎∴S四边形BOCE = BF·EF + (OC +EF)·OF ‎ ‎=( a＋3 )·(－－‎2a＋3) + (－－‎2a＋6)·（－a）……………………………9 分 ‎=………………………………………………………………………10 分 ‎=－+ ‎ ‎∴ 当a =－时，S四边形BOCE 最大, 且最大值为 ．……………………………11 分 ‎ 此时，点E 坐标为 (－，)……………………………………………………12分 解法②：‎ 过点E 作EF⊥x 轴于点F， 设E ( x , y ) ( －3< x < 0 ) …………………………8分 则S四边形BOCE = (3 + y )·(－x) + ( 3 + x )·y ………………………………………9分 ‎ = ( y－x)= ( ) …………………………………10 分 ‎ = － + ‎ ‎∴ 当x =－时，S四边形BOCE 最大，且最大值为 ． …………………………11分 此时，点E 坐标为 (－，) ……………………………………………………12分 ‎【086】⑴证明：∵BC是⊙O的直径 ‎∴∠BAC=90o 又∵EM⊥BC，BM平分∠ABC，‎ ‎∴AM=ME，∠AMN=EMN 又∵MN=MN，‎ ‎∴△ANM≌△ENM ‎⑵∵AB2=AF·AC ‎∴‎ 又∵∠BAC=∠FAB=90o ‎∴△ABF∽△ACB ‎∴∠ABF=∠C 又∵∠FBC=∠ABC+∠FBA=90o ‎∴FB是⊙O的切线 ‎⑶由⑴得AN=EN，AM=EM，∠AMN=EMN，‎ 又∵AN∥ME，∴∠ANM=∠EMN，‎ ‎∴∠AMN=∠ANM，∴AN=AM，‎ ‎∴AM=ME=EN=AN ‎∴四边形AMEN是菱形 ‎∵cos∠ABD=，∠ADB=90o ‎∴‎ 设BD=3x，则AB=5x，，由勾股定理 而AD=12，∴x=3‎ ‎∴BD=9，AB=15‎ ‎∵MB平分∠AME，∴BE=AB=15‎ ‎∴DE=BE-BD=6‎ ‎∵ND∥ME，∴∠BND=∠BME，又∵∠NBD=∠MBE ‎∴△BND∽△BME，则 设ME=x，则ND=12-x，，解得x=‎ ‎∴S=ME·DE=×6=45‎ ‎【087】（天门）略 ‎【088】解：（1）法一：由图象可知：抛物线经过原点，‎ 设抛物线解析式为．‎ 把，代入上式得： 1分 解得 3分 ‎∴所求抛物线解析式为 4分 法二：∵，，‎ ‎∴抛物线的对称轴是直线．‎ 设抛物线解析式为（） 1分 把，代入得 ‎ 解得 3分 ‎∴所求抛物线解析式为． 4分 ‎（2）分三种情况：‎ ‎①当，重叠部分的面积是，过点作轴于点，‎ ‎2‎ O A B C x y ‎1‎ ‎1‎ ‎3‎ P 第26题图1‎ Q F ‎∵，在中，，，‎ 在中，，，‎ ‎∴，‎ ‎2‎ O A B C x y ‎1‎ ‎1‎ ‎3‎ 第26题图2‎ Q F G P H ‎∴． 6分 ‎②当，设交于点，作轴于点，‎ ‎，则四边形是等腰梯形，‎ 重叠部分的面积是．‎ ‎∴，‎ ‎∴． 8分 ‎③当，设与交于点，交于点，重叠部分的面积是 ‎．‎ 因为和都是等腰直角三角形，所以重叠部分的面积是．‎ ‎2‎ O A B C x y ‎1‎ ‎1‎ ‎3‎ 第26题图3‎ Q F M P N ‎∵，，‎ ‎∴，‎ ‎∴，‎ ‎∴‎ ‎ ． 10分 ‎（3）存在 12分 ‎ 14分 ‎【089】解：（1）圆心在坐标原点，圆的半径为1，‎ 点的坐标分别为 抛物线与直线交于点，且分别与圆相切于点和点，‎ ‎． 2分 点在抛物线上，将的坐标代入 ‎，得： 解之，得：‎ 抛物线的解析式为：． 4分 ‎（2）‎ 抛物线的对称轴为，‎ O x y N C D E F B M A P ‎． 6分 连结，‎ ‎，，‎ 又，‎ ‎，‎ ‎． 8分 ‎（3）点在抛物线上． 9分 设过点的直线为：，‎ 将点的坐标代入，得：，‎ 直线为：． 10分 过点作圆的切线与轴平行，点的纵坐标为，‎ 将代入，得：．‎ 点的坐标为， 11分 当时，，‎ 所以，点在抛物线上． 12分 说明：解答题各小题中只给出了1种解法，其它解法只要步骤合理、解答正确均应得到相应的分数．‎ ‎【090】（1）解：把A（，0），C（3，）代入抛物线 得 ‎ 1分 ‎ 整理得 ……………… 2分 解得………………3分 ‎ ∴抛物线的解析式为 4分 ‎ （2）令 解得 ‎ ‎ ∴ B点坐标为（4，0） ‎ ‎ 又∵D点坐标为（0，）　　∴AB∥CD ∴四边形ABCD是梯形．‎ D O B A x y C B C y=kx+1‎ 图(9) -1‎ H T ‎ ∴S梯形ABCD ＝ 5分 设直线与x轴的交点为H， ‎ 与CD的交点为T，‎ 则H（，0）， T（，） 6分 ‎∵直线将四边形ABCD面积二等分 ‎∴S梯形AHTD ＝S梯形ABCD＝４‎ E F M N G O B A x y 图(9) -2‎ ‎∴ 7分　‎ ‎∴ 8分 ‎（3）∵MG⊥轴于点G，线段MG︰AG＝1︰2‎ ‎ ∴设M（m，）， 9分 ‎ ‎∵点M在抛物线上 ∴ ‎ 解得（舍去） 10分 ‎∴M点坐标为（3，） 11分 根据中心对称图形性质知，MQ∥AF，MQ＝AF，NQ＝EF，‎ ‎∴N点坐标为（1，） 12分 ‎【091】(1)解：法1：由题意得 ……1分 ‎ 解得 ……2分 ‎ 法2：∵ 抛物线y＝x2－x＋c的对称轴是x＝， ‎ ‎ 且 －(－1) ＝2－，∴ A、B两点关于对称轴对称. ‎ ‎ ∴ n＝2n－1 ……1分 ‎ ∴ n＝1，c＝－1. ……2分 ‎ ∴ 有 y＝x2－x－1 ……3分 ‎ ＝(x－)2－. ‎ ‎ ∴ 二次函数y＝x2－x－1的最小值是－. ……4分 ‎ ‎ (2)解：∵ 点P(m，m)(m＞0)，‎ ‎ ∴ PO＝m.‎ ‎ ∴ 2≤m ≤＋2.‎ ‎ ∴ 2≤m≤1＋. ……5分 ‎ 法1： ∵ 点P(m，m)(m＞0)在二次函数y＝x2－x＋c的图象上，‎ ‎ ∴ m＝m2－m＋c，即c＝－m2＋‎2m.‎ ‎ ∵ 开口向下，且对称轴m＝1，‎ ‎ ∴ 当2≤m≤1＋ 时， ‎ ‎ 有 －1≤c≤0. ……6分 ‎ 法2：∵ 2≤m≤1＋，‎ ‎ ∴ 1≤m－1≤.‎ ‎ ∴ 1≤(m－1)2≤2. ‎ ‎ ∵ 点P(m，m)(m＞0)在二次函数y＝x2－x＋c的图象上，‎ ‎ ∴ m＝m2－m＋c，即1－c＝(m－1)2.‎ ‎ ∴ 1≤1－c≤2.‎ ‎ ∴ －1≤c≤0. ……6分 ‎ ∵ 点D、E关于原点成中心对称，‎ ‎ 法1： ∴ x2＝－x1，y2＝－y1.‎ ‎ ∴ ‎ ∴ 2y1＝－2x1， y1＝－x1. ‎ ‎ 设直线DE：y＝kx.‎ ‎ 有 －x1＝kx1.‎ ‎ 由题意，存在x1≠x2. ‎ ‎ ∴ 存在x1，使x1≠0. ……7分 ‎ ∴ k＝－1.‎ ‎ ∴ 直线DE： y＝－x. ……8分 ‎ 法2：设直线DE：y＝kx.‎ ‎ 则根据题意有 kx＝x2－x＋c，即x2－(k＋1) x＋c＝0.‎ ‎ ∵ －1≤c≤0，‎ ‎ ∴ (k＋1)2－‎4c≥0.‎ ‎ ∴ 方程x2－(k＋1) x＋c＝0有实数根. ……7分 ‎ ∵ x1＋x2＝0， ‎ ‎ ∴ k＋1＝0.‎ ‎ ∴ k＝－1.‎ ‎ ∴ 直线DE： y＝－x. ……8分 ‎ 若 则有 x2＋c＋＝0.即 x2＝－c－.‎ ‎ ① 当 －c－＝0时，即c＝－时，方程x2＝－c－有相同的实数根，‎ ‎ 即直线y＝－x与抛物线y＝x2－x＋c＋有唯一交点. ……9分 ‎ ② 当 －c－＞0时，即c＜－时，即－1≤c＜－时，‎ ‎ 方程x2＝－c－有两个不同实数根，‎ ‎ 即直线y＝－x与抛物线y＝x2－x＋c＋有两个不同的交点. ……10分 ‎ ③ 当 －c－＜0时，即c＞－时，即－＜c≤0时，‎ ‎ 方程x2＝－c－没有实数根，‎ ‎ 即直线y＝－x与抛物线y＝x2－x＋c＋没有交点. ……11分 ‎【092】解：A B C （1）如图，在坐标系中标出O，A，C三点，连接OA，OC．‎ ‎∵∠AOC≠90°， ∴∠ABC=90°，‎ 故BC⊥OC， BC⊥AB，∴B（，1）．（1分，）‎ 即s=，t=1．直角梯形如图所画．（2分）‎ ‎（大致说清理由即可）‎ ‎（2）由题意，y=x2+mx－m与 y=1（线段AB）相交， ‎ 得， （3分）∴1＝x2+mx－m，‎ 由 (x－1)(x+1+m)=0，得． ‎ ‎∵=1<，不合题意，舍去． （4分）‎ ‎∴抛物线y=x2+mx-m与AB边只能相交于（，1）， ‎ ‎ ∴≤－m－1≤，∴ ． ①（5分） ‎ 又∵顶点P()是直角梯形OABC的内部和其边上的一个动点，‎ ‎∴，即 ． ② （6分） ‎ ‎∵，‎ ‎（或者抛物线y=x2+mx－m顶点的纵坐标最大值是1）‎ ‎∴点P一定在线段AB的下方． （7分） ‎ 又∵点P在x轴的上方，‎ ‎∴，‎ ‎∴ ． （*8分）‎ ③（9分） ‎ 又∵点P在直线y=x的下方，∴，（10分）即 ‎ （*8分处评分后，此处不重复评分）‎ ‎ ④ ‎ ‎ 由①②③④ ，得．（12分） ‎ ‎ 说明：解答过程，全部不等式漏写等号的扣1分，个别漏写的酌情处理．‎ ‎【093】解：（1）连结与交于点，则当点运动到点时，直线平分矩形的面积．理由如下：‎ ‎　　∵矩形是中心对称图形，且点为矩形的对称中心．‎ ‎　　又据经过中心对称图形对称中心的任一直线平分此中心对称图形的面积，因为直线 过矩形的对称中心点，所以直线平分矩形的面积．…………2分 ‎　　由已知可得此时点的坐标为．‎ ‎　　设直线的函数解析式为．‎ 则有　解得，．‎ 所以，直线的函数解析式为：． 5分 ‎（2）存在点使得与相似．‎ 如图，不妨设直线与轴的正半轴交于点．‎ 因为，若△DOM与△ABC相似，则有或．‎ 当时，即，解得．所以点满足条件．‎ 当时，即，解得．所以点满足条件．‎ 由对称性知，点也满足条件．‎ 综上所述，满足使与相似的点有3个，分别为、、． 9分 ‎（3）如图 ，过D作DP⊥AC于点P，以P为圆心，半径长为画圆，过点D分别作的切线DE、DF，点E、F是切点．除P点外在直线AC上任取一点P1，半径长为画圆，过点D分别作的切线DE1、DF1，点E1、F1是切点．‎ 在△DEP和△DFP中，∠PED＝∠PFD，PF＝PE，PD＝PD，∴△DPE≌△DPF．‎ ‎∴Ｓ四边形DEPF＝2Ｓ△DPE＝2×．‎ ‎∴当DE取最小值时，Ｓ四边形DEPF的值最小．‎ ‎∵，，‎ ‎∴．‎ ‎∵，∴．‎ ‎∴．由点的任意性知：DE是 点与切点所连线段长的最小值．……12分 在△ADP与△AOC中，∠DPA＝∠AOC，‎ ‎∠DAP＝∠CAO， ∴△ADP∽△AOC．‎ ‎∴，即．∴．‎ ‎∴．‎ ‎∴Ｓ四边形ＤＥＰＦ＝，即Ｓ＝． 14分 ‎（注：本卷中所有题目，若由其它方法得出正确结论，请参照标准给分．）‎ ‎【094】解：（1）令二次函数，则 ‎ 1分 ‎ 2分 过三点的抛物线的解析式为 4分 ‎（2）以为直径的圆圆心坐标为 ‎ 5分 为圆切线 6分 ‎ ‎ ‎ 8分 ‎ ‎ 坐标为 9分 ‎（3）存在 10分 抛物线对称轴为 设满足条件的圆的半径为，则的坐标为或 而点在抛物线上 ‎ ‎ 故在以为直径的圆，恰好与轴相切，该圆的半径为， 12分 注：解答题只要方法合理均可酌情给分 ‎【095】（1）（4，0），． 2分 ‎． 4分 ‎（2）是直角三角形． 5分 证明：令，则．‎ ‎．‎ ‎． 6分 解法一：． 7分 ‎．‎ 是直角三角形． 8分 解法二：‎ ‎，‎ ‎． 7分 ‎．‎ ‎，‎ ‎．即．‎ 是直角三角形． 8分 G A O B x y 图1‎ D E F H C ‎（3）能．当矩形两个顶点在上时，如图1，交于．‎ ‎，‎ ‎．‎ ‎． 9分 解法一：设，则，，‎ ‎．‎ ‎=． 10分 当时，最大．‎ ‎．‎ ‎，‎ ‎．‎ ‎，． 11分 解法二：设，则．‎ ‎． 10分 当时，最大．‎ ‎．‎ ‎，‎ ‎．‎ C A O B x y 图2‎ D G G ‎，． 11分 当矩形一个顶点在上时，与重合，如图2，‎ ‎，‎ ‎．‎ ‎．‎ 解法一：设，，‎ ‎．‎ ‎=． 12分 当时，最大．‎ ‎，．‎ ‎ 13分 解法二：设，，，，．．‎ ‎= 12分 当时，最大，‎ ‎．．‎ ‎ 13分 综上所述：当矩形两个顶点在上时，坐标分别为，（2，0）；‎ 当矩形一个顶点在上时，坐标为 14分 ‎【096】（1）因所求抛物线的顶点M的坐标为(2,4)，‎ 故可设其关系式为 ………………(1分)‎ 又抛物线经过O(0,0)，于是得， ………………(2分)‎ 解得 a=-1 ………………(3分)‎ ‎∴ 所求函数关系式为，即. ……………(4分)‎ ‎（2）① 点P不在直线ME上. ………………(5分)‎ 根据抛物线的对称性可知E点的坐标为(4,0)，‎ 又M的坐标为(2,4)，设直线ME的关系式为y=kx+b.‎ 于是得 ，解得 所以直线ME的关系式为y=-2x+8. ……(6分)‎ 由已知条件易得，当t时，OA=AP， ……………(7分)‎ ‎∵ P点的坐标不满足直线ME的关系式y=-2x+8. ‎ ‎∴ 当t时，点P不在直线ME上. ………………(8分)‎ ‎② S存在最大值. 理由如下： ………………(9分)‎ ‎∵ 点A在x轴的非负半轴上，且N在抛物线上， ∴ OA=AP=t.‎ ‎∴ 点P，N的坐标分别为(t,t)、(t,-t 2+4t) ∴ AN=-t 2+4t (0≤t≤3) ,‎ ‎∴ AN-AP=(-t 2+4 t)- t=-t 2+3 t=t(3-t)≥0 , ∴ PN=-t 2+3 t …(10分)‎ ‎（ⅰ）当PN=0，即t=0或t=3时，以点P，N，C，D为顶点的多边形是三角形，此三角形的高为AD，∴ S=DC·AD=×3×2=3. ………………(11分)‎ ‎（ⅱ）当PN≠0时，以点P，N，C，D为顶点的多边形是四边形 ‎∵ PN∥CD，AD⊥CD，‎ ‎∴ S=(CD+PN)·AD=[3+(-t 2+3 t)]×2=-t 2+3 t+3=‎ 其中(0＜t＜3)，由a=-1，0＜＜3，此时. …………(12分)‎ 综上所述，当t时，以点P，N，C，D为顶点的多边形面积有最大值，‎ 这个最大值为. ………………(13分)‎ 说明：（ⅱ）中的关系式，当t=0和t=3时也适合.‎ ‎【097】解：（1）点的坐标为． （2分）‎ ‎（2）抛物线的表达式为． （4分）‎ y O C D B ‎6‎ A x A M P1‎ P2‎ ‎（3）抛物线的对称轴与轴的交点符合条件．‎ ‎∵，‎ ‎∴．‎ ‎∵，‎ ‎∴． （6分）‎ ‎∵抛物线的对称轴，‎ ‎∴点的坐标为． （7分）‎ 过点作的垂线交抛物线的对称轴于点．‎ ‎∵对称轴平行于轴，‎ ‎∴．‎ ‎∵，‎ ‎∴． （8分）‎ ‎∴点也符合条件，．‎ ‎∴，‎ ‎∴． （9分）‎ ‎∴．‎ ‎∵点在第一象限，‎ ‎∴点的坐标为，‎ ‎∴符合条件的点有两个，分别是，． （11分）‎ ‎【098】解：（1）当t=4时，B(4,0)‎ 设直线AB的解析式为y= kx+b .‎ 把 A(0,6)，B(4,0) 代入得：‎ ‎ , 解得： ,‎ ‎∴直线AB的解析式为：y=－x+6.………………………………………4分 ‎(2) 过点C作CE⊥x轴于点E 由∠AOB=∠CEB=90°，∠ABO=∠BCE，得△AOB∽△BEC.‎ ‎∴，‎ ‎∴BE= AO=3，CE= OB= ，‎ ‎∴点C的坐标为(t+3，).…………………………………………………………2分 方法一：‎ y O C A B x D E S梯形AOEC= OE·(AO+EC)= (t+3)(6+)=t2+t+9，‎ S△ AOB= AO·OB= ×6·t=3t，‎ S△ BEC= BE·CE= ×3×= t，‎ ‎∴S△ ABC= S梯形AOEC－ S△ AOB－S△ BEC ‎ = t2+t+9－3t－t = t2+9.‎ 方法二：‎ ‎∵AB⊥BC，AB=2BC，∴S△ ABC= AB·BC= BC2.‎ 在Rt△ABC中，BC2= CE2+ BE2 = t2+9，‎ 即S△ ABC= t2+9.…………………………………………………………2分 y O C A B x D E ‎(3)存在，理由如下：‎ ‎①当t≥0时. ‎ Ⅰ.若AD＝BD.‎ 又∵BD∥y轴 ‎∴∠OAB=∠ABD，∠BAD=∠ABD，‎ ‎∴∠OAB=∠BAD.‎ 又∵∠AOB=∠ABC，‎ ‎∴△ABO∽△ACB，‎ ‎∴，‎ ‎∴= ，‎ ‎∴t=3，即B(3，0).‎ Ⅱ.若AB＝AD.‎ 延长AB与CE交于点G，‎ 又∵BD∥CG ‎∴AG＝AC y O C A B D E H G x 过点A画AH⊥CG于H．‎ ‎∴CH＝HG＝CG 由△AOB∽△GEB，‎ 得＝ ，‎ ‎∴GE= .‎ 又∵HE＝AO＝６，CE＝ ‎∴＋６＝×（＋）‎ y O C A B x D E F ‎∴t2-24t-36=0‎ 解得：t=12±6. 因为 t≥0，‎ 所以t=12＋6，即B(12＋6，0).‎ Ⅲ.由已知条件可知，当0≤t<12时，∠ADB为钝角，故BD ≠ AB.‎ ‎ 当t≥12时，BD≤CE