20112012中考数学总复习资料四边形3综合练习 4页

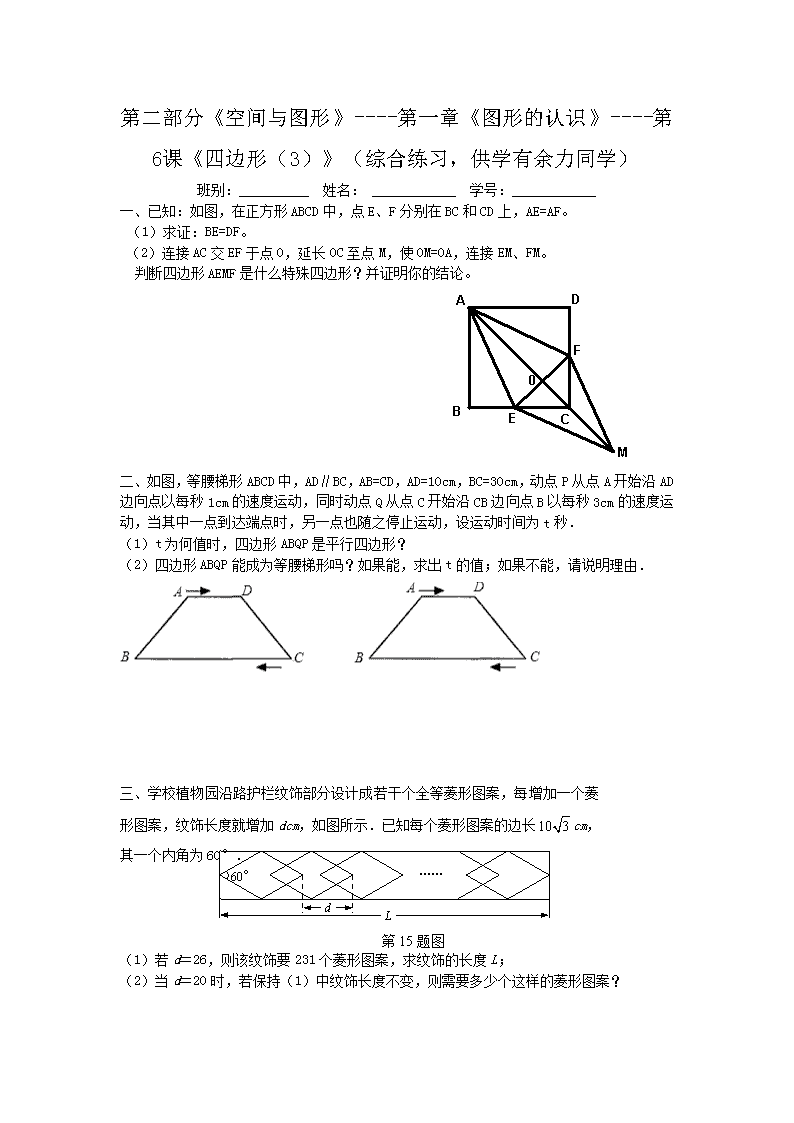
第二部分《空间与图形》----第一章《图形的认识》----第6课《四边形（3）》（综合练习，供学有余力同学）‎ 班别：__________ 姓名： ____________ 学号：____________‎ 一、已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE=AF。‎ ‎（1）求证：BE=DF。‎ ‎（2）连接AC交EF于点O，延长OC至点M，使OM=OA，连接EM、FM。‎ 判断四边形AEMF是什么特殊四边形？并证明你的结论。‎ 二、如图，等腰梯形ABCD中，AD∥BC，AB=CD，AD=10cm，BC=30cm，动点P从点A开始沿AD边向点以每秒1cm的速度运动，同时动点Q从点C开始沿CB边向点B以每秒3cm的速度运动，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒．‎ ‎（1）t为何值时，四边形ABQP是平行四边形？‎ ‎（2）四边形ABQP能成为等腰梯形吗？如果能，求出t的值；如果不能，请说明理由．‎ ‎60°‎ ‎……‎ d L 三、学校植物园沿路护栏纹饰部分设计成若干个全等菱形图案，每增加一个菱形图案，纹饰长度就增加dcm，如图所示．已知每个菱形图案的边长cm，其一个内角为60°．‎ 第15题图 ‎（1）若d＝26，则该纹饰要231个菱形图案，求纹饰的长度L；‎ ‎（2）当d＝20时，若保持（1）中纹饰长度不变，则需要多少个这样的菱形图案？‎ 四、如图，正方形ABCD的边长为1，G是CD边上的一个动点（G不与C、D重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE、BG，并延长BG交DE于点H．‎ ‎（l）求证：①△BCG≌△DCE；②BH⊥DE．‎ ‎（2）当点G运动到何处时，四边形DGEF是平行四边形，并加以证明．‎ ‎（3）当点G运动到何处时，BH垂直平分DE？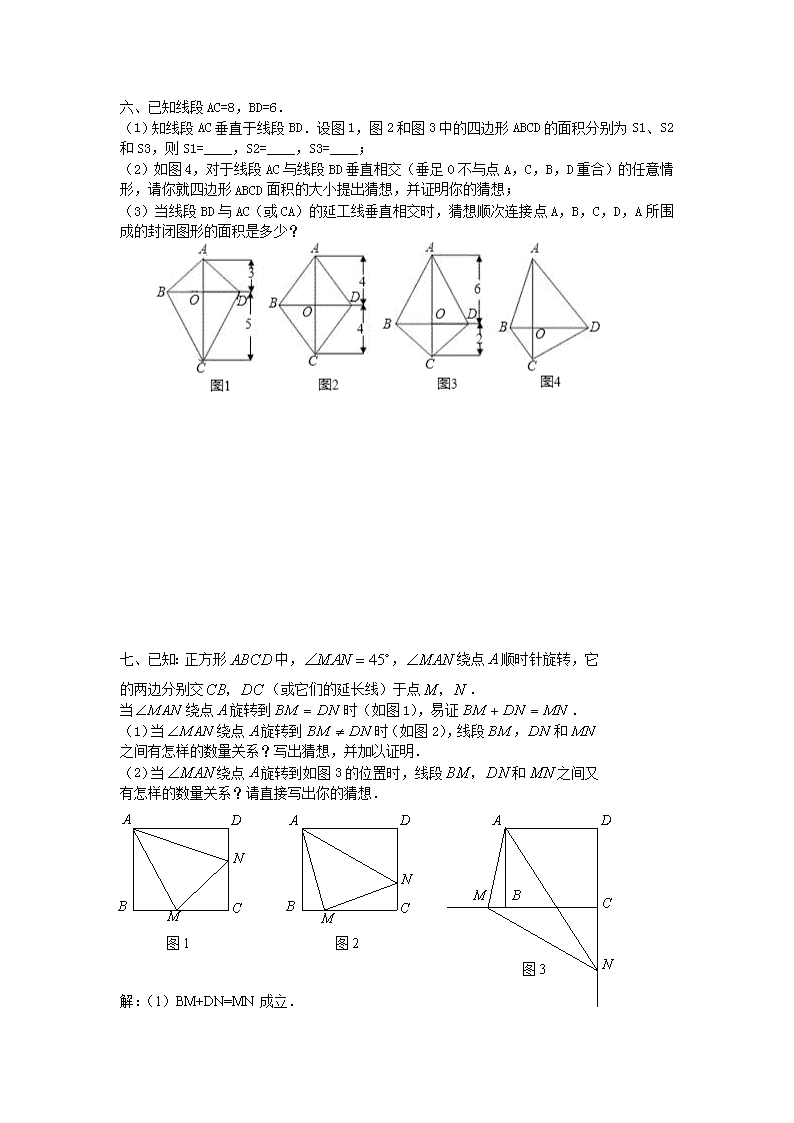请说明理由．‎ 五、白色卷综合 六、已知线段AC=8，BD=6．‎ ‎（1）知线段AC垂直于线段BD．设图1，图2和图3中的四边形ABCD的面积分别为S1、S2和S3，则S1=____，S2=____，S3=____；‎ ‎（2）如图4，对于线段AC与线段BD垂直相交（垂足O不与点A，C，B，D重合）的任意情形，请你就四边形ABCD面积的大小提出猜想，并证明你的猜想；‎ ‎（3）当线段BD与AC（或CA）的延工线垂直相交时，猜想顺次连接点A，B，C，D，A所围成的封闭图形的面积是多少？‎ 七、已知：正方形中，，绕点顺时针旋转，它的两边分别交（或它们的延长线）于点．‎ 当绕点旋转到时（如图1），易证．‎ ‎（1）当绕点旋转到时（如图2），线段和之间有怎样的数量关系？写出猜想，并加以证明．‎ ‎（2）当绕点旋转到如图3的位置时，线段和之间又有怎样的数量关系？请直接写出你的猜想．‎ B M B C N C N M 图1‎ B C N M 图2‎ 图3‎ A A A D D D 解：（1）BM+DN=MN成立．‎ B C N M 图2‎ E A D 证明：如图，把△ADN绕点A顺时针旋转90°，‎ 得到△ABE，则可证得E、B、M三点共线（图形画正确）．‎ ‎∴∠EAM=90°-∠NAM=90°-45°=45°，‎ 又∵∠NAM=45°，‎ ‎∴△AEM≌△ANM，‎ ‎∴ME=MN，‎ ‎∵ME=BE+BM=DN+BM，‎ ‎∴DN+BM=MN； （2）DN-BM=MN．‎ 八、已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．‎ ‎（1）求证：EG=CG；‎ ‎（2）将图①中△BEF绕B点逆时针旋转45º，如图②所示，取DF 中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．‎ ‎（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（不要求证明）‎ A D C E G 第24题图②分析图 F H D F B A D C E G 第24题图②‎ F B A C E 第24题图③‎ F B A D C E G 第24题图①‎ B 解：（1）证明：在Rt△FCD中，∵G为DF的中点，∴ CG= FD．………1分 同理，在Rt△DEF中，EG= FD．…………2分∴ CG=EG．…………………3分 ‎（2）（1）中结论仍然成立，即EG=CG．…………………………4分 ‎（证明思路是构造两个全等三角形，下面是简单的思路分析：请同学们写出详细的证明过程）‎ 思路分析：如图所示，延长EF交CD于点H，连接GH；‎ 易证四边形EBCH是矩形得BE=CH；‎ 易证△BEF是等腰直角三角形得BE=EF；‎ 从而得CH=EF，∠BFE=45°，从而∠GFE=135°；‎ 易证△DHF也是等腰直角三角形，而且GH是它底边上的中线，‎ 从而得GH是它顶角平分线，得∠GFH=∠GHF=45°，从而得GH=GF，∠GHC=135°；‎ 从而得∠GFE=∠GHC=135°；‎ 在△GEF与△GCH中，∵CH=EF，∠GFE=∠GHC=135°，GH=GF，‎ ‎∴△GEF≌△△GCH．∴EG=CG．‎ ‎（3）（1）中的结论仍然成立，即EG=CG．其他的结论还有:EG⊥CG．‎